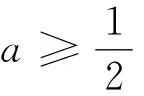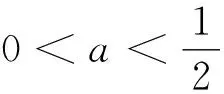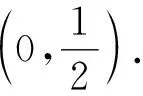穩(wěn)中求變 變中出新 新中見能 甄別素養(yǎng)
——2023年高考數(shù)學全國乙卷評析

陳靖逸 王 勇

湖北省襄陽市第一中學 (441000)

2023年高考數(shù)學全國乙卷試題注重基礎(chǔ),強化學科素養(yǎng),考查關(guān)鍵能力,突出對創(chuàng)新應用能力的考查.試題關(guān)注社會發(fā)展,引導考生運用所學數(shù)學知識解決生活實際問題,富有時代氣息,體現(xiàn)了“穩(wěn)中求變、變中出新、新中見能”的命題理念.試題以數(shù)學基礎(chǔ)知識、基本技能、基本思想方法為支撐點和立足點,注重對數(shù)學通性通法的考查.文、理科試卷針對考生群體的不同數(shù)學水平,精心設(shè)計,合理布局,準確區(qū)分考生.試題加強教考銜接,服務(wù)“雙減”政策落實,助力基礎(chǔ)教育提質(zhì)增效.試題有利于科學選擇人才,有利于深化課程改革,有利于促進社會公平,對培養(yǎng)考生的創(chuàng)新精神、實踐能力,提升考生核心素養(yǎng)有積極的導向作用.

一、對選擇題的評析

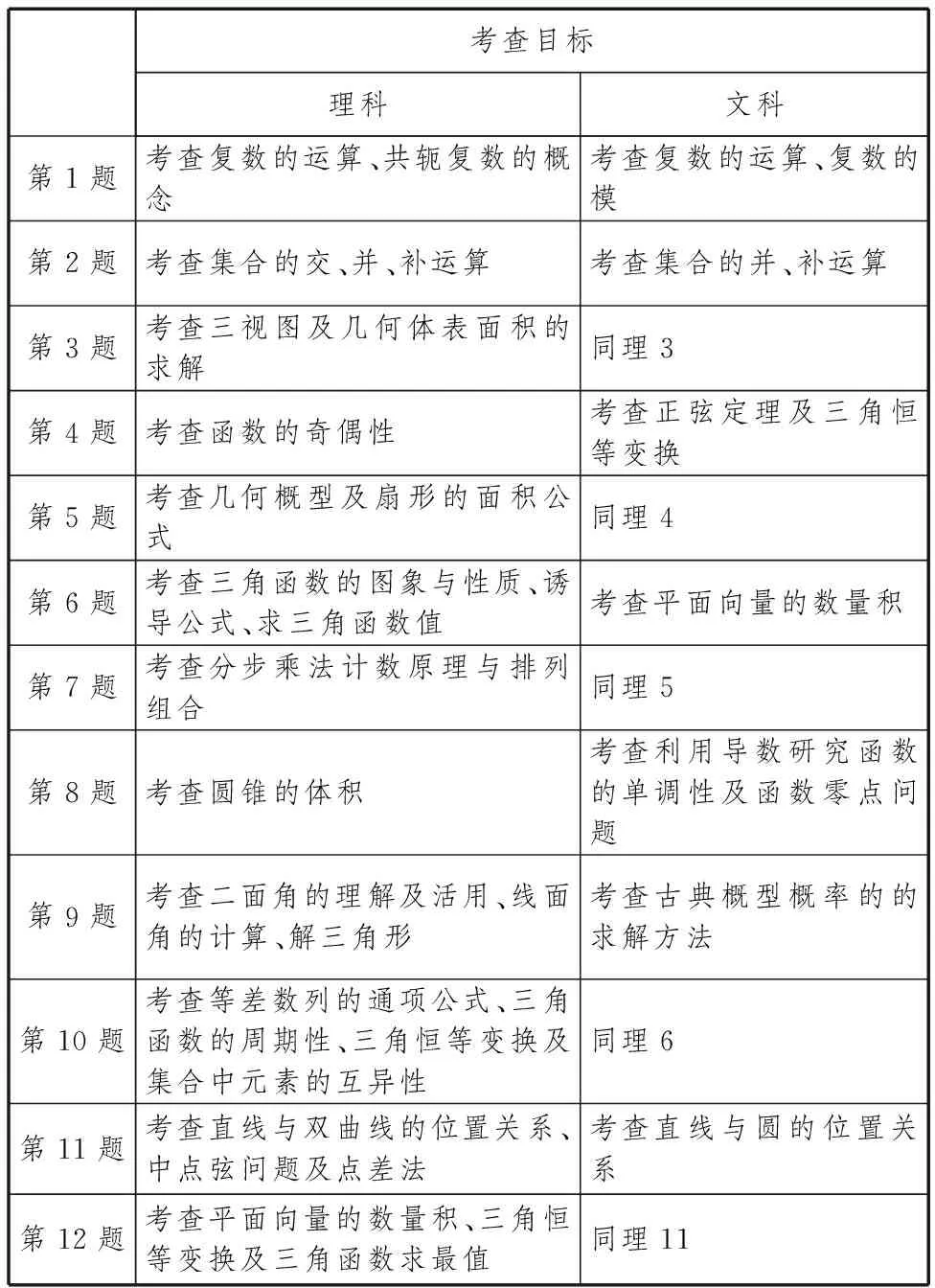
考查目標理科文科第1題考查復數(shù)的運算、共軛復數(shù)的概念考查復數(shù)的運算、復數(shù)的模第2題考查集合的交、并、補運算考查集合的并、補運算第3題考查三視圖及幾何體表面積的求解同理3第4題考查函數(shù)的奇偶性考查正弦定理及三角恒等變換第5題考查幾何概型及扇形的面積公式同理4第6題考查三角函數(shù)的圖象與性質(zhì)、誘導公式、求三角函數(shù)值考查平面向量的數(shù)量積第7題考查分步乘法計數(shù)原理與排列組合同理5第8題考查圓錐的體積考查利用導數(shù)研究函數(shù)的單調(diào)性及函數(shù)零點問題第9題考查二面角的理解及活用、線面角的計算、解三角形考查古典概型概率的的求解方法第10題考查等差數(shù)列的通項公式、三角函數(shù)的周期性、三角恒等變換及集合中元素的互異性同理6第11題考查直線與雙曲線的位置關(guān)系、中點弦問題及點差法考查直線與圓的位置關(guān)系第12題考查平面向量的數(shù)量積、三角恒等變換及三角函數(shù)求最值同理11

其中理科第10題、理科第11題(文科第12題)、理科第12題頗有研討價值,下面分別解析,供研讀.

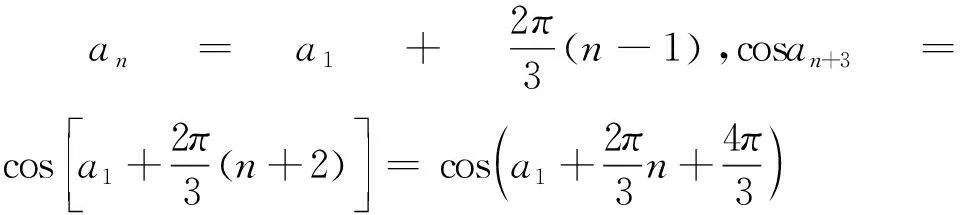
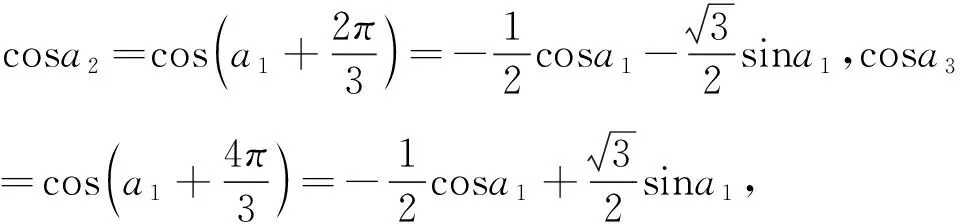
②當cosa1=cosa3≠cosa2時,有cosa1=

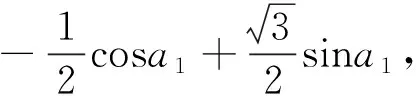
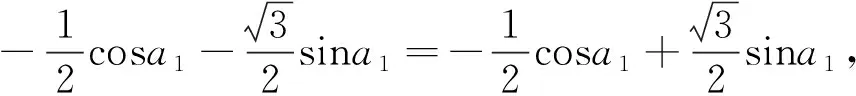
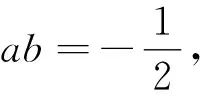
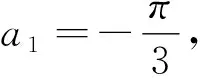
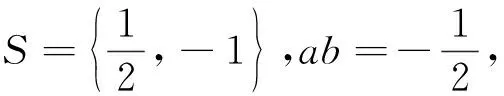
點評：本題將數(shù)列、三角函數(shù)、集合等知識結(jié)合起來,設(shè)問簡潔,角度新穎,考查知識全面,著重考查考生的理性思維和數(shù)學探索等學科素養(yǎng),考查分類討論思想,要求考生靈活應用所學知識解決綜合性問題,有較強的選拔作用.

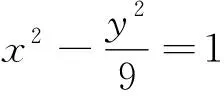
A.(1,1) B.(-1,2) C.(1,3) D.(-1,-4)

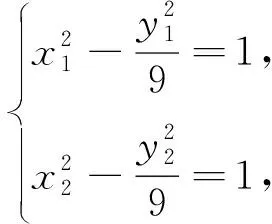
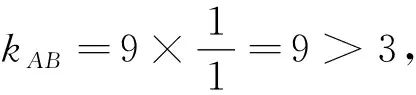
點評：本題將中點弦問題和直線與雙曲線的位置關(guān)系有機整合,設(shè)問角度新穎,重點考查數(shù)形結(jié)合思想和邏輯推理能力,考生需將問題轉(zhuǎn)化為判斷直線AB與雙曲線是否有兩個交點,逐一驗證選項是否正確,考查考生靈活運用所學知識解決綜合問題的能力,在注重考查基礎(chǔ)知識的同時,對考生的思維能力要求較高,具有較好的選拔功能.

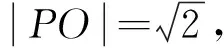
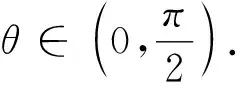
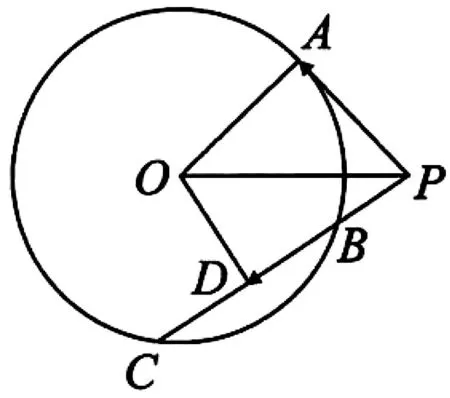
圖1

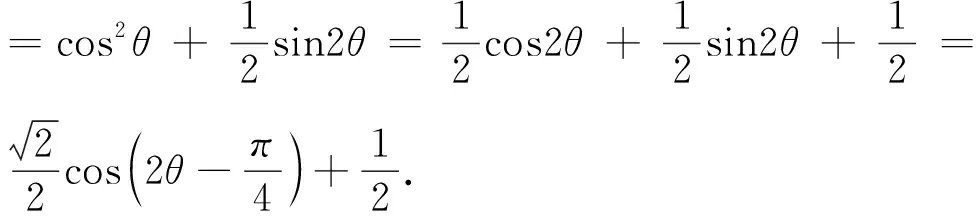
點評：本題解法多樣,靈活性強,綜合性強,考查直觀想象、理性思維等素養(yǎng),試題重基礎(chǔ)、重能力,在考查平面幾何和三角知識的同時,有效考查了數(shù)形結(jié)合思想和轉(zhuǎn)化與化歸思想,為考生提供了多層次的思考空間.

二、對填空題的評析

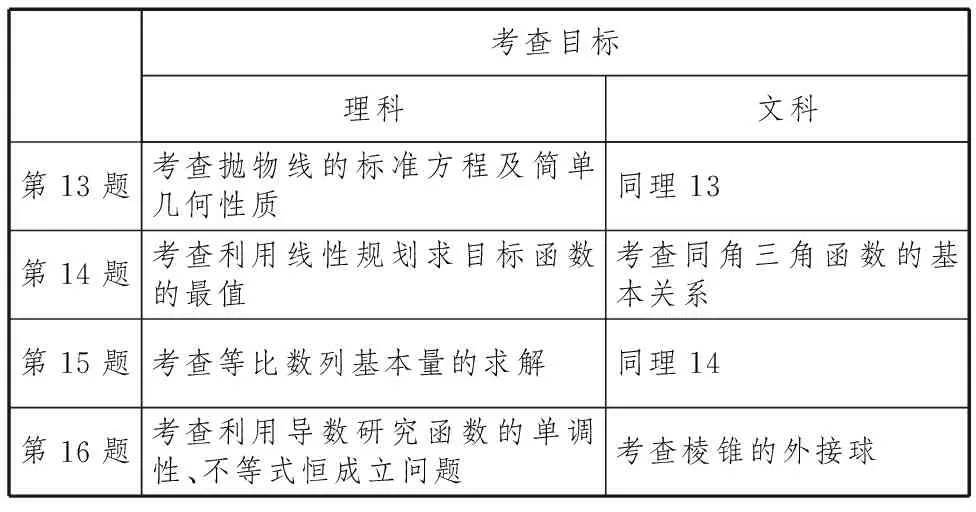
考查目標理科文科第13題考查拋物線的標準方程及簡單幾何性質(zhì)同理13第14題考查利用線性規(guī)劃求目標函數(shù)的最值考查同角三角函數(shù)的基本關(guān)系第15題考查等比數(shù)列基本量的求解同理14第16題考查利用導數(shù)研究函數(shù)的單調(diào)性、不等式恒成立問題考查棱錐的外接球

其中理科第16題、文科第16題值得認真研究和品味.

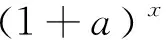
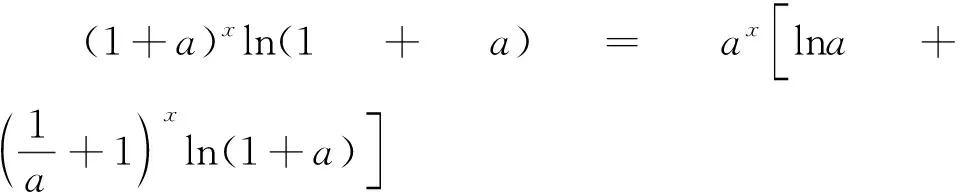
點評：本題考查參數(shù)的取值范圍問題,試題看似復雜,但基本原理簡單,考查了函數(shù)遞增的充要條件,充分說明了高考更注重對基礎(chǔ)知識、基本思想的考查,緊扣課程標準.

例5 (文16)已知點S,A,B,C均在半徑為2的球面上,ΔABC是邊長為3的等邊三角形,SA⊥平面ABC,則SA=________．

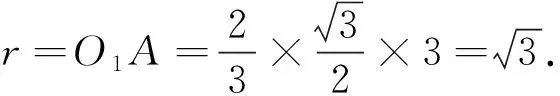
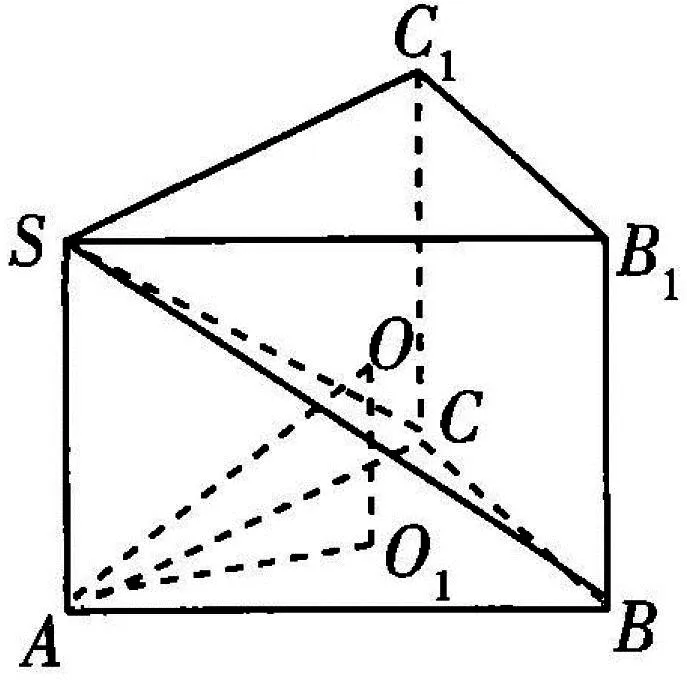
圖2

點評：棱錐的外接球問題是高中數(shù)學的重點內(nèi)容,難點在于找到外接球球心的位置,本題主要考查考生的空間想象能力和運算求解能力,試題簡潔明了,注重考查基礎(chǔ)知識,屬于常規(guī)題,增強了考生自信心,促進考生正常發(fā)揮,同時也反映出高考數(shù)學更加注重對基礎(chǔ)知識的考查,而不是一味變花樣地增加難度.

三、對解答題的評析

1.統(tǒng)計題——中規(guī)中矩送大禮

本題考查樣本平均數(shù)、方差,利用樣本數(shù)據(jù)特征估計總體,體現(xiàn)了數(shù)據(jù)分析、數(shù)學建模、數(shù)學運算等核心素養(yǎng).本題與考生平時的訓練題極為相似,絕大多數(shù)考生當笑納“大禮”.

2.三角題——平平淡淡考功底

理科三角題考查利用正弦定理、余弦定理解三角形,三角形的面積公式,考查數(shù)形結(jié)合思想、轉(zhuǎn)化與化歸思想,體現(xiàn)了數(shù)學運算、邏輯推理等核心素養(yǎng).數(shù)學功底扎實的考生對于本題所用的破解“招法”諳熟于心,順利求解當不成問題.

3.數(shù)列題——常見題型穩(wěn)情緒

文科數(shù)列題考查等差數(shù)列的通項公式、分段數(shù)列求和,考查轉(zhuǎn)化與化歸思想、分類討論思想,體現(xiàn)了數(shù)學運算、邏輯推理等核心素養(yǎng).本題題型常規(guī),跟考生平時的訓練題類似,彰顯了命題者對考生的人文關(guān)懷,有利于激發(fā)考生的解題興趣,穩(wěn)定考生的情緒.

4.立體幾何題——想說愛你不容易

理科題考查直線與平面平行的判定、平面與平面垂直的判定、二面角的正弦值的求解;文科題是理科題的姊妹題,考查直線與平面平行的判定、三棱錐的體積.這兩題考查轉(zhuǎn)化與化歸思想,體現(xiàn)了直觀想象、邏輯推理、數(shù)學運算等核心素養(yǎng).本題貌似簡單,其實暗藏玄機,考生求解起來并不順利,從考試結(jié)果看,該題得分率偏低.

5.解析幾何題——精打細算求真理

本題考查直線與橢圓的位置關(guān)系、橢圓中的定點問題等,考查數(shù)形結(jié)合思想、轉(zhuǎn)化與化歸思想,體現(xiàn)了邏輯推理、數(shù)學運算等核心素養(yǎng).第(1)問由點A在C上得出b2的值,結(jié)合離心率和a2=b2+c2求出a2的值,進而得出C的方程;第(2)問由題意知直線PQ的斜率存在且不為0,設(shè)出直線PQ的方程和P(x1,y1),Q(x2,y2),與橢圓方程聯(lián)立,由根與系數(shù)的關(guān)系得出x1+x2和x1x2,寫出直線AP的方程求出點M的縱坐標yM,同理易得點N的縱坐標yN,通過計算得出yM+yN=6,進而得出MN的中點為定點(0,3).本題第(2)問運算量較大,有一定的難度,具有較好的區(qū)分和選拔功能.

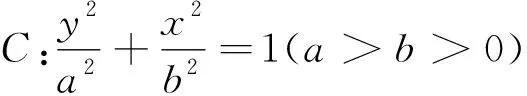
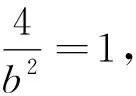
(2)如圖3,由題意知,直線PQ的斜率存在且不為0,設(shè)lPQ:y-3=k(x+2),P(x1,y1),Q(x2,y2),由

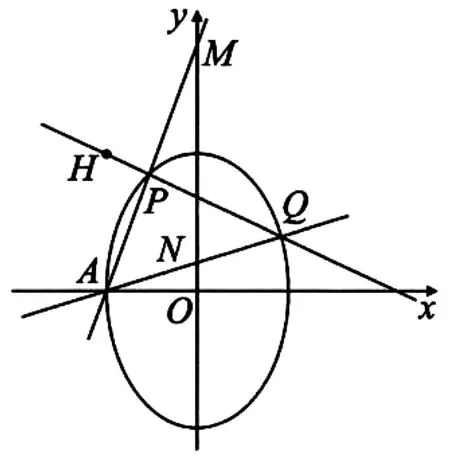
圖3

點評：本題與2022年全國乙卷解析幾何題相似,都考查圓錐曲線的定點問題,但難度較2022年有所降低,主要考查理性思維、數(shù)學探索學科素養(yǎng),考查直觀想象和數(shù)學運算能力,通過本題也能看出2023年高考數(shù)學在出題風格和設(shè)問方式上與2022年類似,要想得高分,應注重基礎(chǔ)知識和基本思想、基本方法,多研究近幾年的高考題,而不是一味地刷題,追求難度,從而真正實現(xiàn)“雙減”又高效備考的目的.

6.函數(shù)與導數(shù)題——分段得分巧智取

理科第21題函數(shù)與導數(shù)題考查導數(shù)的幾何意義、函數(shù)圖象的對稱性、利用導數(shù)研究函數(shù)的極值.第(1)問考查曲線在某點處的切線;第(2)問由曲線的對稱性求參數(shù)的值;第(3)問由函數(shù)存在極值求參數(shù)的取值范圍.

文科第21題函數(shù)與導數(shù)題是理科第21題的姊妹題,考查導數(shù)的幾何意義、利用導數(shù)研究函數(shù)的單調(diào)性.第(1)問同理科第(1)問;第(2)問由函數(shù)的單調(diào)性求參數(shù)的取值范圍,難度明顯降低,切合文科考生的數(shù)學實際.

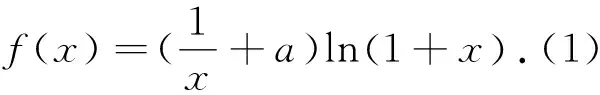
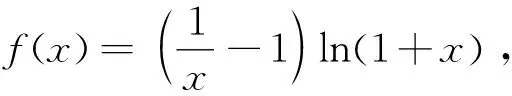
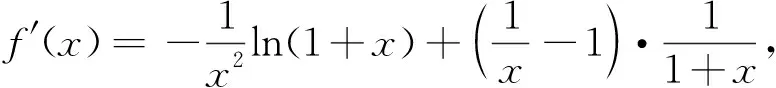
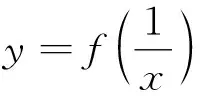
①當a≤0時,2a-1<0,當x>0時,h′(x)<0,所以h(x)在(0,+∞)上單調(diào)遞減,所以當x>0時,h(x)

點評：本題以含參數(shù)的復雜函數(shù)為載體,通過對切線方程、函數(shù)圖象的對稱性及函數(shù)極值點的考查,滲透著數(shù)學中大膽猜測,小心驗證的基本思維方式.重點考查分類討論思想,突出對數(shù)學學科基本概念、基本原理的考查,強調(diào)知識之間的內(nèi)在聯(lián)系,注重本原性方法,淡化特殊技巧,強調(diào)對通性通法的深入理解和綜合運用,促進學生將知識和方法內(nèi)化為自身的能力.

7.二選一選考題——中規(guī)中矩合情理

選考題第22題考查極坐標方程與直角坐標方程的互化、參數(shù)方程與普通方程的互化、直線與圓的位置關(guān)系.選考題第23題考查絕對值不等式的解法、不等式組確定的平面區(qū)域的面積.這兩選考題意在考查考生的運算求解能力、邏輯推理能力及函數(shù)與方程思想、轉(zhuǎn)化與化歸思想、數(shù)形結(jié)合思想等,難易適中,題型常規(guī),與考生平時的訓練題類似,考生志在必得.

總之,2023年高考數(shù)學全國乙卷試題閃光著理性思維的光芒,以問題情境設(shè)置為載體,考查核心價值和能力素養(yǎng).試題聚焦學科主干知識,突出學科關(guān)鍵能力,關(guān)注社會生活和實踐應用,很好地體現(xiàn)了“一核四層四翼”的考查要求,很好地把握了穩(wěn)定、改革與創(chuàng)新之間的關(guān)系,彰顯了立德樹人價值引領(lǐng)與核心素養(yǎng)育人導向.