是“錯題”,還是“正解”?——
——離散型分布列取值概率可以為0嗎?

王楷文

安徽省合肥市第六中學 (230001)

一、問題發現

在學習了離散型分布列時,教輔資料中有這樣一道題:

設p為非負實數,隨機變量X的分布列為

X012P12-pp12

則E(X)的最大值為________,D(x)的最大值為________.

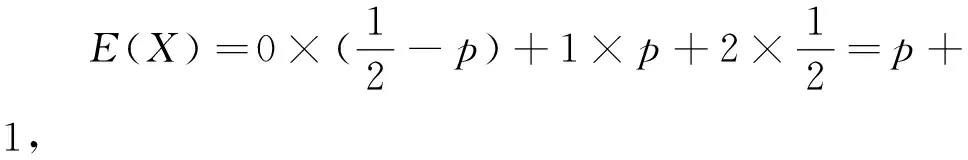
根據古典概型的定義,知當p=0時,離散型隨機變量X=1對應的試驗結果沒有發生,即當p=0時這個試驗的結果只有兩個結果X=0與X=2,而沒有X=1這個結果,此時分布列表中的X=1就多余了,是這個題目有錯誤,還是我們對于教材內容的理解不到位呢?筆者所在學校使用的是北師大版教材,2019年12月第1版(2022年7月第5次印刷)的選擇性必修第一冊第198頁關于離散型分布列的性質寫道:(1)pi>0,i=1,2,…,n,…;(2)p1+p2+…+pn+…=1.由此看出,北師大版教材關于離散型隨機變量取值的概率不能為0,基于此認識,知此題是錯題.

但人教A版選擇性必修第三冊(2020年3月第1版)第58頁關于分布列的性質介紹如下:(1)pi≥0,i=1,2,…,n;(2)p1+p2+…+pn=1.顯然教材給出的隨機變量取值的概率是pi≥0,i=1,2,…,n,而不是pi>0,i=1,2,…,n,…,這種情況說明是的確存在隨機變量取值可以為零的情況,還是“pi≥0,i=1,2,…,n”中等號是多余的呢?基于人教版教材中對于離散型隨機變量的定義,如果離散型隨機變量的某一個取值對應的事件是存在的,且其概率為零,那么上述解答就是正確的.

面對如此現象,作為教師該如何處理呢?

二、問題解決

由于一個試驗的每一個試驗結果稱為樣本點,而試驗結果究竟是什么,與試驗所要求是什么結果有關,如拋擲一枚質地均勻的骰子,如果按照正面向上個數是什么,則試驗的結果就有6個,即樣本點有6個;如果按照骰子向上的點數是奇數還是偶數,則試驗的結果就有2個:向上的點數是奇數與向上的點數為偶數,即樣本點有2個,由此可知,將一個試驗的所有基本事件按照一定的標準進行分類整合也可產生新的樣本點,由于每一個樣本點ω都能用唯一的實數X(ω)與之對應,則稱X為隨機變量,例如,拋擲一枚質地均勻的骰子,隨機變量可以是X=1,2,3,4,5,6,也可以是Y=0,1(其中0代表向上的點數為偶數,1代表向上的點數為奇數),基于此認識,請看例子:在(1,5)中取一個數,可將試驗結果分為三類(1,3),3,(3,5),不妨記作隨機變量X=1,2,3(其中1表示區間(1,3),2表示點3處,3表示區間(3,5)處),則由幾何概型知,P(X=3)=0,但X=3對應的事件是有可能發生的,即概率等于0的事件不代表不可能發生.

正是因為我們可以將幾何概型試驗的結果按照一定的標準進行分類整合若干部分作為隨機變量,而每一部分的試驗結果均可以用一個數字表示,這樣獲得的離散型隨機變量的取值概率有可能為零,且這個變量取值對應的試驗結果也是有可能發生的,基于此認識,我們有理由認為上述問題的解答是正確的.

三、問題思考

在教學中,遇到一些困惑問題是正常的,但面對困惑時,我們教師是客觀冷靜地弄清楚問題的真相,還是一棍子打死,武斷地認為此題是錯題,這兩種截然不同的態度,反映了我們教師兩種對待教學的態度,是認真地作潛心研究,還是不加深思認為是錯題?古人云:“師者,傳道授業解惑也”,這句話教師都能耳熟能詳,但遇到困惑時,往往回避的多,深入研究的少,從而會造成教學的“冤假錯案”,如,本題是沒有錯誤的,如果教師告訴學生是錯誤的,那么就造成混淆是非,之所以會出現此種現象,是因為教師有些經驗是不成熟導致的,事實上,受思維定勢的影響,故步自封,我們不少自認為成熟的經驗卻是片面的、不成熟的,對此,不少教師蒙在鼓里,卻自己不知道,如根據北師大教材介紹的離散型隨機變量的性質pi>0,i=1,2,…,n,…,輕易判斷此題是此題,就是有力的例證.

俗話說:“身教勝于言教”、“榜樣的力量是無窮的”,所以在教學中教師要做到為人師表,以給學生樹立榜樣,真正做到立德樹人.況且,在倡導學生深度學習的今天,培養學生學會思考的習慣,是當下教師教育教學的職責,為此教師更應該做到深度學習,試想:如果一個教師在教學中遇到疑難問題需要深入研究時,卻回避了之,那么怎能引導學生進行深入思考呢?學生的核心素養如何發展呢?實際上,只有讓學生參與問題研究的情境過程中,才能真正發展學生的素養,對此,應引起我們教師深思!

總之,在教學中遇到一時難以化解的問題,教師摒棄“那種沒有經過一番深度思考,而僅憑經驗感覺行事,主觀臆斷是非曲直”的做法,而應該以積極的心態應對,通過查資料、與同行研討、深思細悟、傾聽學生想法等多方論證,將問題的來龍去脈弄清楚,給學生一個明白的解釋,若是題目錯,要講出錯的原因,若是解答正確,則解答正確的依據是什么,只有這樣,我們的教學才能談得上有深度、有品位、有素養的教學.