推進泵快速啟動水力特性及流場演變研究

張富毅，楊 鵬，鄭楓川，趙曉陽，劉 影

（1.上海船用柴油機研究所，上海 200090；2.北京理工大學機械與車輛學院，北京 100081）

0 引 言

魚雷是一種隱蔽性能強、爆破威力大和攻擊效果好的水中兵器[1]。空氣渦輪泵發射系統是一種常用的魚雷發射裝置[2-3]，其工作原理如圖1所示：發射時，打開發射閥，發射氣瓶中的高壓氣體進入渦輪機，驅動其轉動，渦輪機帶動與海水相連的推進泵快速啟動，通過推進泵旋轉做功提升海水的壓能和動能，并作用在魚雷尾部，推動魚雷出管[4]。整個發射過程耗時極短，通常小于1 s，處于強瞬態過程，推進泵是發射系統的關鍵核心部件，其水力性能的優劣直接決定魚雷出管的速度、加速度以及出管后的位移等，為實現魚雷高航速、大深度、遠航程和低噪聲的目標，有必要深入研究推進泵在快速啟動過程中的水力特性及流場演變。

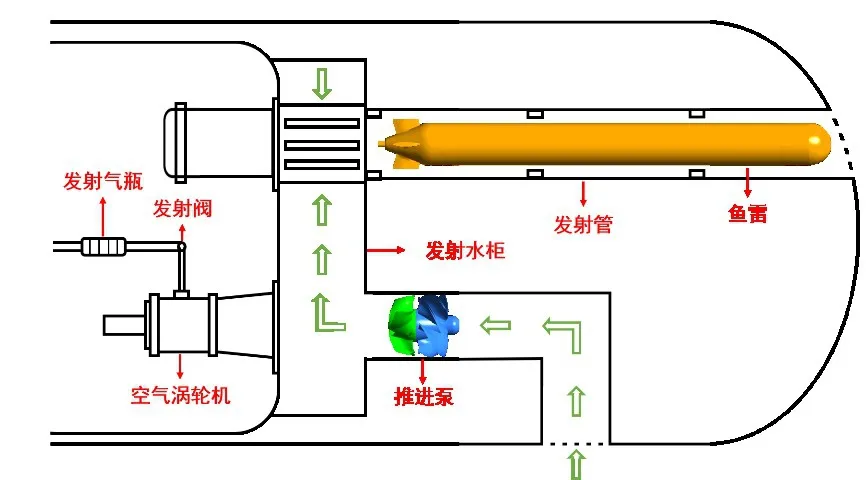
圖1 空氣渦輪泵發射系統示意圖Fig.1 Schematic diagram of air turbopump launching system

國內外學者針對葉片泵的啟動過程開展了系列研究。Dazin 等[5-6]提出了葉片泵啟動過程中揚程的理論計算方法，并成功預測一臺離心泵啟動過程中的瞬態揚程；張德勝等[7]也通過混流泵啟動試驗驗證了瞬態揚程理論模型的正確性。Zhang等[8-9]提出水力機械的廣義歐拉方程，該方程是由穩定工況的歐拉方程和瞬態過程中所產生的附加理論揚程組成，并指出附加理論揚程由旋轉加速揚程和流動慣性揚程兩部分組成，同時發現，外特性參數的瞬態變化只與角加速度項有關，而與流動慣性項無關。

Duplaa[10]對離心泵進行了快速啟動試驗研究，通過瞬時扭矩、流量、進出口壓力和轉速描述離心泵的運行特性。Wu等[11]搭建了離心泵啟動試驗臺用于研究加速度對瞬態特性的影響，發現以高加速度啟動可以較快地達到穩定狀態，但是沖擊揚程明顯增大，并且瞬態性能會因空泡的產生而嚴重下降。李偉等[12]建立了混流泵啟動過程瞬態外特性和壓力脈動測量系統，研究不同啟動時間和不同流量下瞬態壓力脈動特性，結果表明，在啟動結束時刻，當流量一定時，壓力沖擊隨啟動時間的增加逐漸減弱，當啟動時間一定時，進口壓力沖擊隨流量增大逐漸減弱甚至消失，而葉輪中部和出口的壓力逐漸增強。陳宗賀[13]采用高速攝影測量方法觀測到混流泵啟動初期的空化主要由葉頂泄漏渦引起的渦空化和附著在葉片壁面上的附著型空化組成，并隨著轉速增大，空化區域從葉片壓力面中部靠近輪緣處向葉片壓力面后緣及輪轂方向發展。李偉等[14]采用數值方法研究了混流泵啟動過程進口處的流動特性，發現葉片吸力面流動分離和葉頂間隙泄漏是導致進口回流的主要因素，回流參數隨時間呈現先增大后減小的趨勢，且主流與回流軸向速度在啟動初期呈對稱分布。楊敬江等[15]以雙蝸殼離心泵為研究對象建立了一套循環管路系統，通過非定常計算發現，在啟動初期，蝸殼內部流速變化劇烈，蝸殼入口處存在明顯的速度梯度；在啟動過程中，隔板初始位置和末端位置的壓力脈動幅值相對較大，且隔板外側的壓力脈動相對于隔板內側更穩定。

綜上所述，國內外學者采用理論、試驗和數值等方法研究了離心泵和混流泵的啟動過程，但是關于軸流式推進泵啟動瞬態過程的研究尚未涉及，而軸流式推進泵的幾何結構、功能作用和工作環境與常規的離心泵和混流泵相差較大。基于此，本文采用數值模擬方法研究魚雷發射推進泵在不同啟動時間條件下的水力特性以及流場演變，并分析相關流動機理。

1 數值模型及方法

1.1 數值模型

圖2為本文所研究的推進泵模型，包含葉輪和導葉兩部分，葉輪有6個葉片，導葉有8個葉片。推進泵的主要設計參數為：葉輪直徑D=304.8 mm，揚程H=11.9 m，流量Q=580 kg/s，功率為76 kW，轉速n=1450 r/min。

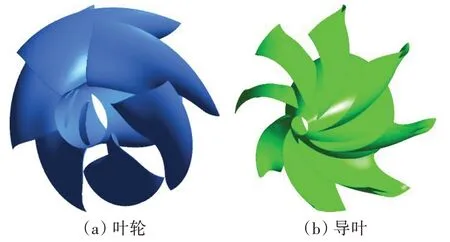
圖2 推進泵模型Fig.2 Model of propulsion pump

數值計算域如圖3 所示，考慮推進泵前后管道和外部水域，外部六面體水域的長寬高分別為30D、10D和20D，入口段管道長為3D，水平出口段管道和豎直出口段管道長為7D。外部水域靠近管道的側面為壁面，其余5個側面為開放邊界，管道和推進泵葉片均為壁面。不同區域間使用交界面連接，葉輪與入口段、葉輪與導葉之間使用Transient Rotor Interface 交界面，其余使用Stage Average Velocity 交界面。整個裝置處于15 m 水深處，環境壓力為248 325 Pa，忽略重力因素。

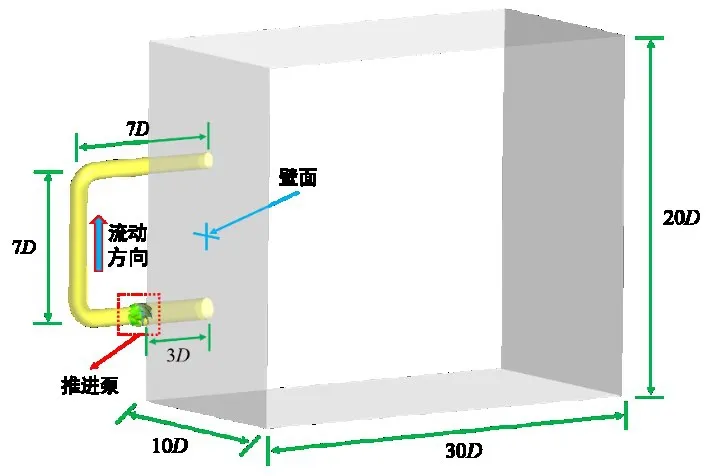
圖3 計算域Fig.3 Computational domain

采用結構化網格劃分計算域，管道和推進泵的網格如圖4所示，在管道和葉片近壁面區布置邊界層網格，彎管和推進泵區域進行局部加密。推進泵區域的網格數量直接決定計算的精度和效率，文獻[16]對設計工況下的推進泵區域進行了網格無關性分析，最終確定推進泵區域網格數為382 萬；管道網格數為143 萬，直管段沿流動方向每0.01 m 布置一個節點，彎管段沿流動方向布置90 個節點，即每隔1°布置一個節點，管道圓周方向布置120 個節點，即每隔3°布置一個節點；外部水域網格數為120萬，計算域總網格數為645萬，網格質量在0.32以上。

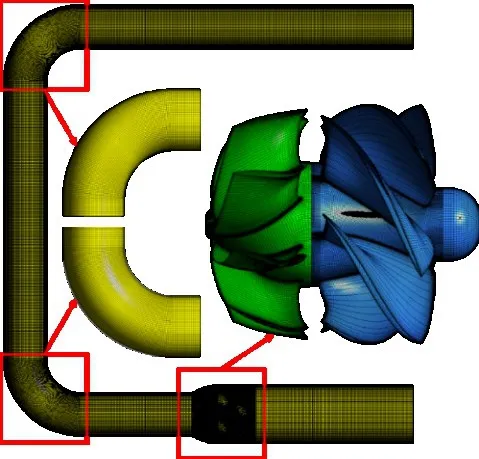
圖4 網格Fig.4 Mesh

1.2 數值方法

采用雷諾時均方法求解連續性方程和動量方程：

式中，i、j表示笛卡爾坐標方向，x為笛卡爾坐標軸，u為速度，ρ為密度，p為壓力，μ和μt分別為層流和湍流黏性系數。

采用SSTk-ω湍流模型，湍動能k方程和湍流頻率ω方程[17]分別為

式中，Pk和Pω為湍流生成項，Dk為湍流耗散項，σk和σω2分別為湍動能k和湍流頻率ω的普朗特數，F1和F2為混合函數，S為剪切應變率，Cω、βω和α為模型常數。

規定推進泵線性啟動，轉速變化規律為

式中，ts為啟動時間，分別取0.1 s、0.2 s和0.3 s，啟動過程分為轉速加速和轉速穩定兩個階段，總運行時間為0.5 s，三種工況的轉速變化規律如圖5 所示。計算的時間步長為0.0001 s，每個時間步長內迭代100 步，圖6 給出了啟動時間為0.2 s 工況的收斂過程，由圖可知，整個求解過程殘差小于1.5E-4，并且除了最初小段時間外，其余時間殘差均小于1E-4，計算精度滿足工程要求。

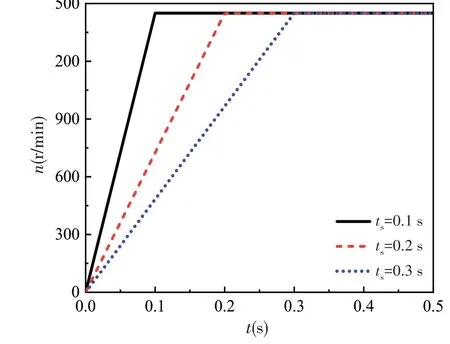
圖5 轉速變化規律Fig.5 Variation of rotational speed

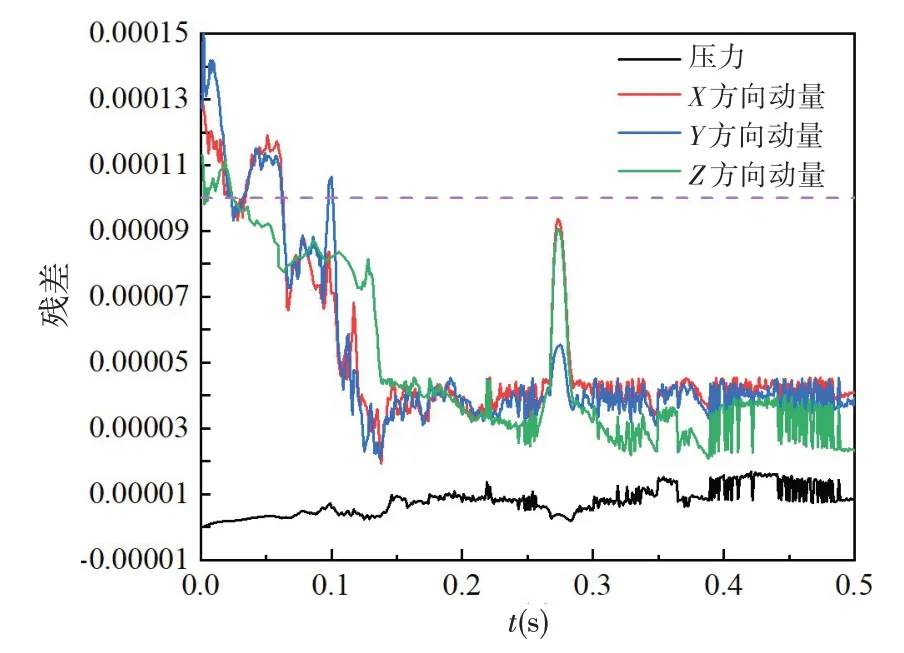
圖6 收斂過程Fig.6 Process of convergence

文獻[18]采用上述數值方法計算得到不同流量下推進泵的外特性參數，并與試驗數據對比，結果表明，推進泵揚程系數、功率系數和效率的數值結果與試驗數據吻合良好，表明上述數值計算方法可以準確預測推進泵外特性。文獻[13]對比了混流泵啟動過程瞬態流場的數值結果和高速攝像測量結果，兩者吻合度良好，表明瞬態數值方法可以準確描述泵內流場演變，而本文的數值方法與文獻[13]一致，可間接說明本文數值研究的可靠性。

2 結果分析

2.1 水力特性分析

圖7給出了流量的演變歷程，由圖可知，流量隨時間持續增加，當轉速增大至穩定值后，流量并未達到穩定值，而是繼續增大；整個過程中，啟動時間越小，流量越大，當運行至0.5 s 時，啟動時間為0.1 s、0.2 s和0.3 s時的流量分別為311.04 kg/s、290.61 kg/s和268.98 kg/s，分別是0.536倍、0.501倍和0.464倍設計流量；而在加速結束瞬間，啟動時間為0.1 s、0.2 s和0.3 s時的流量分別為56.03 kg/s、100.54 kg/s和139.46 kg/s，啟動時間越小，流量越小，相對于轉速變化，滯后程度越強。

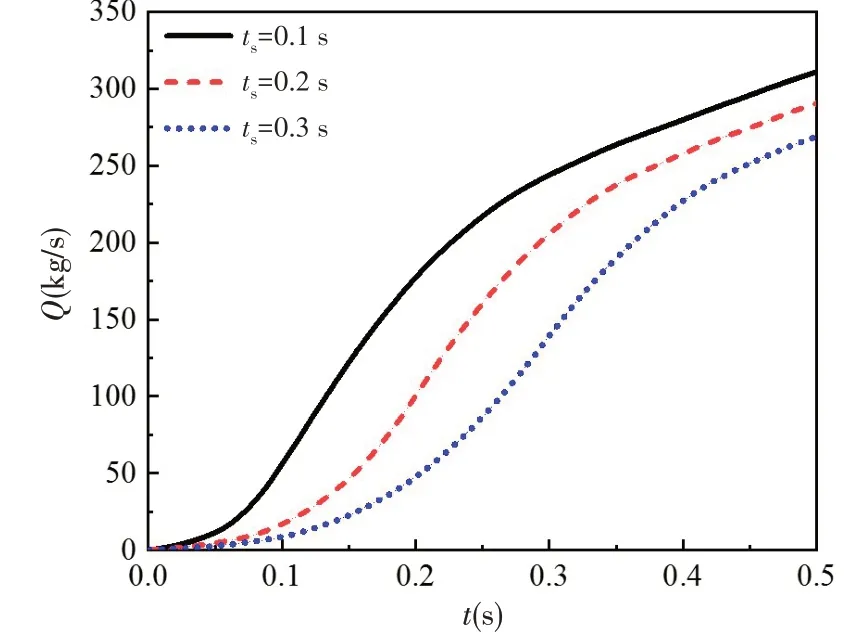
圖7 流量演變歷程Fig.7 Variation of flow rate

由動量定理可知，推力是由流量決定的，所以推力的變化趨勢與流量變化趨勢類似，如圖8所示，推力持續增加，整個過程中，啟動時間越小，推力越大，當運行至0.5 s時，啟動時間為0.1 s、0.2 s和0.3 s時的推力分別為2394.25 N、2089.91 N和1790.54 N，而在加速結束瞬間的推力分別為77.64 N、250.07 N和481.17 N。

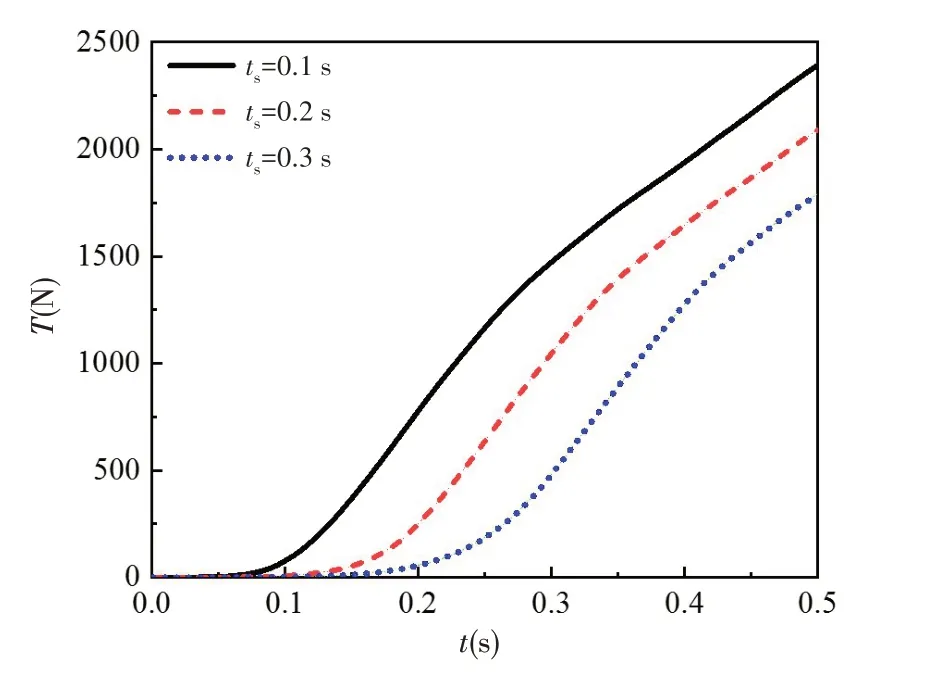
圖8 推力演變歷程Fig.8 Variation of thrust

圖9給出了推進泵進出口壓力的演變歷程，Pin0.1、Pin0.2和Pin0.3分別表示啟動時間為0.1 s、0.2 s和0.3 s時的進口壓力，Pout0.1、Pout0.2和Pout0.3分別表示啟動時間為0.1 s、0.2 s和0.3 s時的出口壓力。由圖可知，啟動瞬間，進出口壓力相同，均為環境壓力；隨后進口壓力先減小后增大，最小值分別為-84.18 kPa、60.91 kPa 和123.43 kPa，最小值隨啟動時間增加而增大；出口壓力先增大后減小，最大值分別為596.75 kPa、520.85 kPa和466.28 kPa，最大值隨啟動時間增大而減小；經過0.5 s的運行，三種工況下的進出口壓力基本一致。進一步分析發現，三種工況下，出口壓力均是在加速結束瞬間達到最大值，而進口壓力均是在加速完成之前就達到最小值；此外，當啟動時間為0.1 s時，進口處壓力的最小值遠低于水的飽和蒸汽壓，說明在推進泵入口處產生大量的空泡，出現嚴重的空化現象。

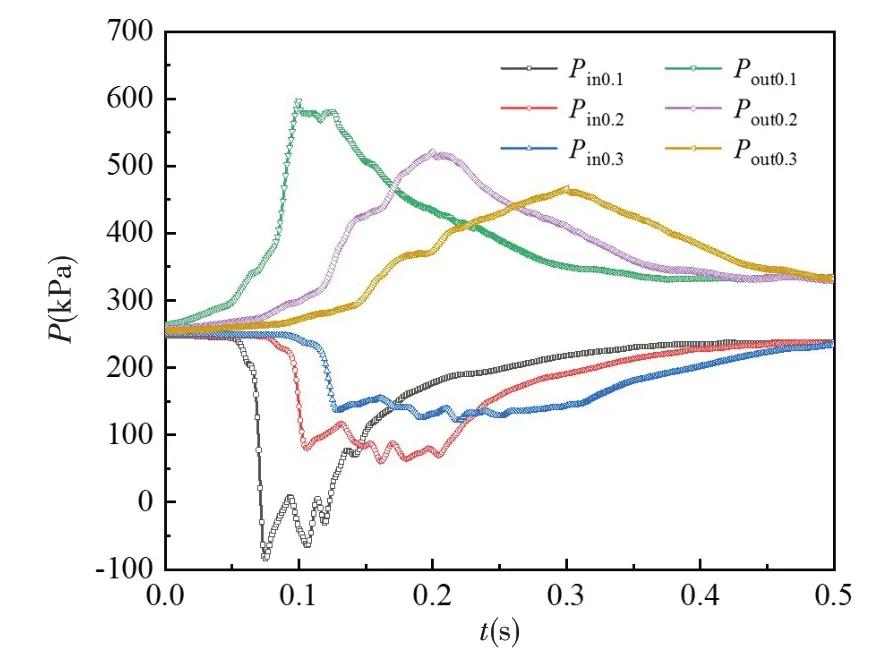
圖9 進出口壓力演變歷程Fig.9 Variation of inlet and outlet pressures

圖10 給出了揚程的演變歷程，揚程主要是由推進泵出口壓力決定的，所以其變化趨勢同出口壓力變化趨勢基本一致，在葉輪加速過程中，快速增大，加速完成后，持續減小，并在加速完成瞬間，存在遠大于設計揚程的沖擊揚程，啟動時間為0.1 s、0.2 s 和0.3 s 時的沖擊揚程分別達到了65.06 m、45.41 m和33.03 m，沖擊揚程隨啟動時間增大而減小，與出口壓力變化規律一致。

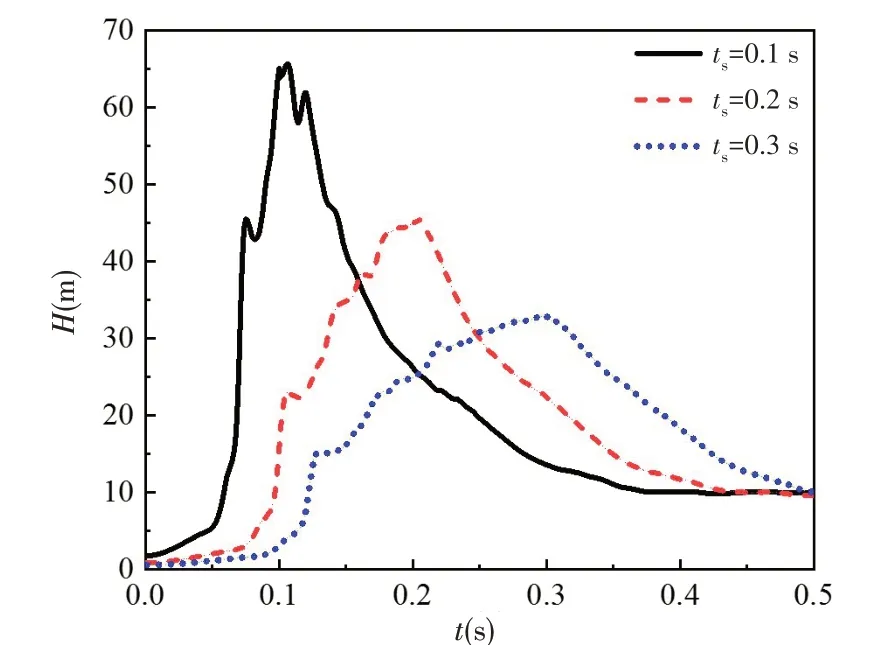
圖10 揚程演變歷程Fig.10 Variation of head

圖11、圖12 和圖13 分別給出了葉輪軸向力、軸向力矩和功率的演變歷程。由圖可知，軸向力、軸向力矩和功率的變化趨勢基本一致，葉輪加速過程中，軸向力、軸向力矩和功率快速增大，加速完成之后，軸向力、軸向力矩和功率持續減小。在加速結束瞬間三者均達到最大值，啟動時間為0.1 s、0.2 s和0.3 s 時軸向力最大值分別為9058.53 N、8730.26 N 和7612.23 N，軸向力矩最大值分別為668.39 N·m、643.41 N·m 和567.37 N·m，功率最大值分別為101.46 kW、97.70 kW 和86.13 kW，軸向力、軸向力矩和功率的最大值均遠大于推進泵的設計值，并且均隨著啟動時間的增大而減小，說明以較高的角加速度啟動推進泵時，葉輪所受到的水流沖擊作用加重。

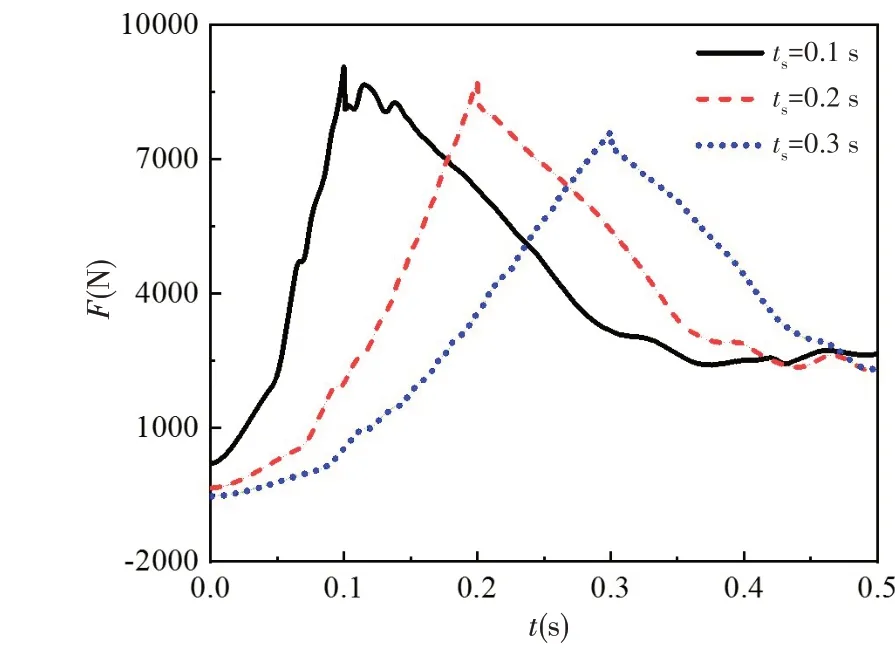
圖11 軸向力演變歷程Fig.11 Variation of axial force

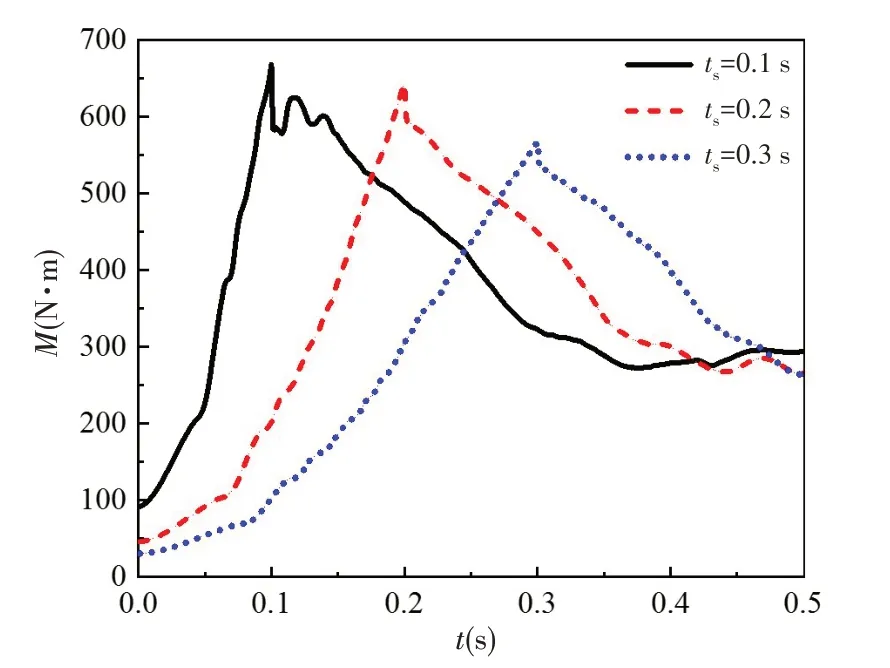
圖12 軸向力矩演變歷程Fig.12 Variation of axial moment

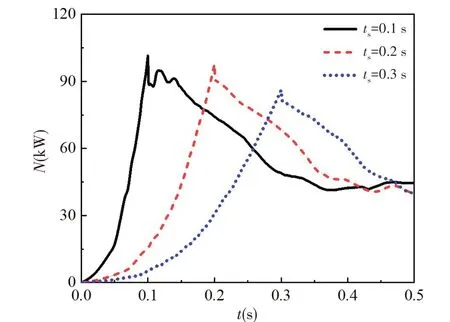
圖13 功率演變歷程Fig.13 Variation of power

圖14 給出了效率的演變歷程。由圖可知，推進泵效率持續增大最終達到相對穩定值，運行至0.5 s時，啟動時間為0.1 s、0.2 s和0.3 s時的效率分別為67.98%、68.54%和66.23%。

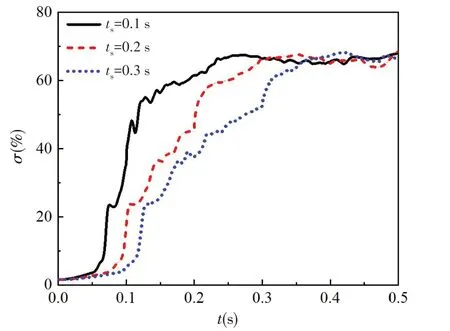
圖14 效率演變歷程Fig.14 Variation of efficiency

2.2 流場演變分析

圖15、圖16和圖17分別為葉輪區域10%、50%和90%葉高展向平面流線分布。由圖可知，在運行初期，葉輪前緣存在強烈的來流沖擊，葉輪通道間產生了嚴重的流動分離和漩渦結構，而葉輪尾緣出現明顯的回流現象，隨著時間的推移，流動逐漸趨于穩定。對比不同啟動時間的10%和50%葉高展向流線分布可以發現，啟動時間越短，流場越快達到穩定狀態；當ts=0.1 s，運行至0.3 s時，漩渦結構基本消除；當ts=0.2 s，運行至0.4 s 時，漩渦結構基本消除；而當ts=0.3 s，運行至0.5 s 時，漩渦結構才基本消除。由于90%葉高平面靠近葉頂位置，流動極其復雜且不穩定，即使運行至0.5 s時，依然存在流動分離、漩渦結構和回流現象，說明推進泵內部依然未達到穩定的流動狀態。

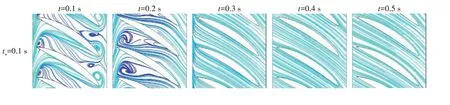
圖15 葉輪區域10%展向表面流線分布Fig.15 Distribution of streamline on 10%span surface of impeller

圖17 葉輪區域90%展向表面流線分布Fig.17 Distribution of streamline on 90%span surface of impeller

圖18為導葉區域軸向平面上的軸向速度分布，其中軸向速度取負值表示該區域產生了回流。由圖可知，當ts=0.1 s，運行至0.1 s時，轉速已經達到最大轉速，但此時入口、中間和出口平面均存在大面積的回流區域；運行至0.2 s 時，三個平面內的回流區域開始減小；當運行至0.5 s 時，入口和出口平面內的回流區域基本消除，而中間平面靠近導葉葉片區域依然存在小面積的回流區域。當ts=0.2 s，運行至0.1 s時，轉速還未達到最大值，三個平面內軸向速度較小，且僅在入口平面存在小面積回流區域；運行至0.2 s時，轉速達到最大值，三個平面內均出現大面積回流區域，隨后回流區面積逐漸減小；運行至0.5 s時，也僅中間平面靠近導葉葉片區域存在小面積的回流區域。當ts=0.3 s，運行至0.1 s時，轉速處于較低水平，軸向速度基本為0且無回流區，運行至0.1 s時，三個平面開始出現較為明顯回流區域；運行至0.3 s時，回流區面積達到最大值，隨后逐漸減小，而當運行至0.5 s時，軸向速度分布規律與ts=0.1 s和ts=0.2 s時類似。

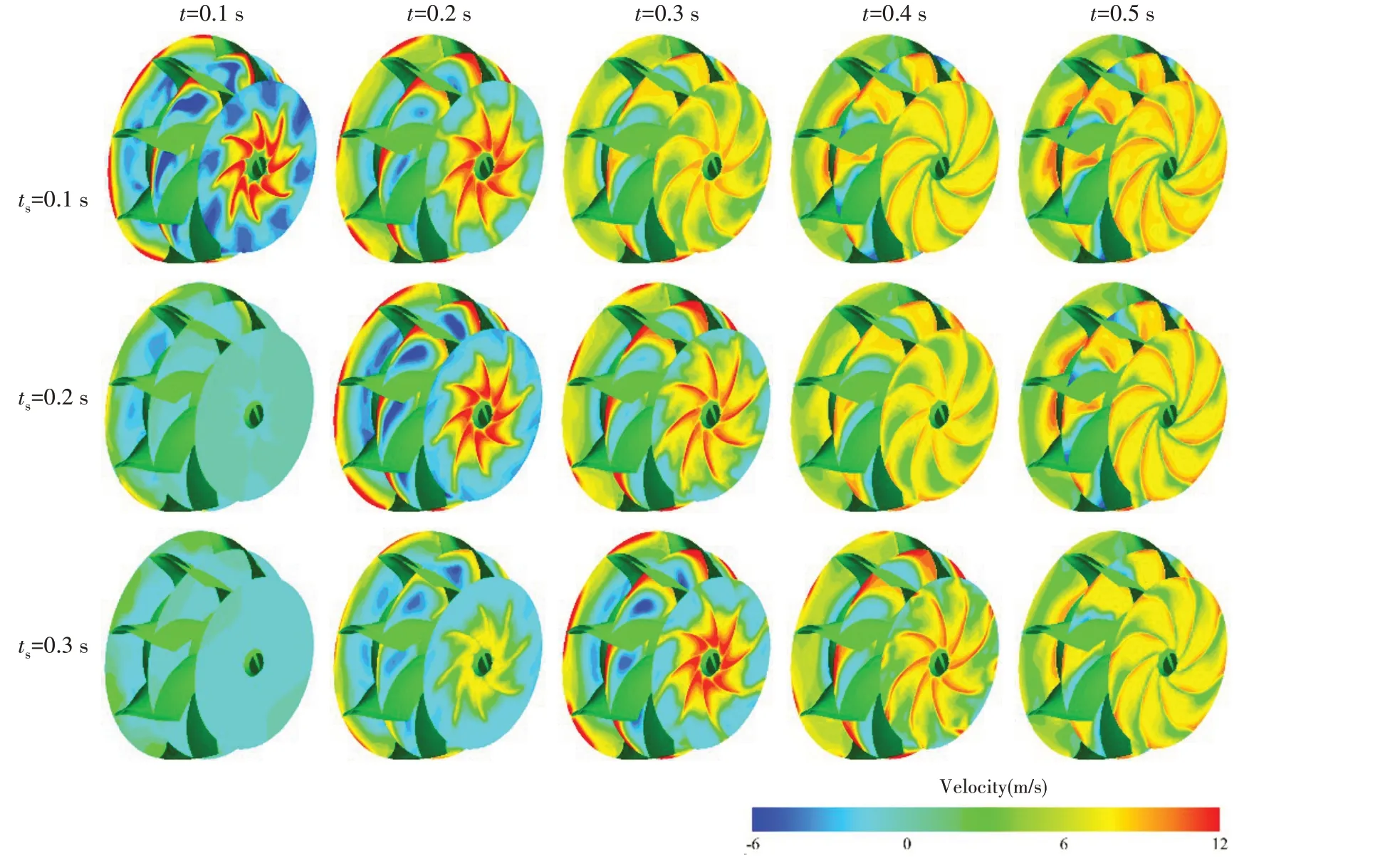
圖18 導葉區域軸向平面速度分布Fig.18 Distribution of axial velocity on axial plane of guide vane

3 結 論

本文采用數值模擬方法研究了魚雷發射推進泵啟動過程中的水力特性和流場演變情況，主要結論如下：

（1）在推進泵啟動過程中，流量和推力隨時間持續增加，揚程、軸向力、軸向力矩和功率隨時間先增大后減小，效率隨時間先增大后保持穩定。揚程、軸向力、軸向力矩和功率在加速結束瞬間存在極大值，且極大值隨著啟動時間的增大而減小。

（2）啟動初期，葉輪區域存在嚴重的來流沖擊、流動分離和漩渦結構，導葉區域的入口、中間和出口平面存在大面積回流區域，隨著時間推移，流場逐漸趨于穩定。啟動時間對推進泵流場演變具有顯著影響，啟動時間越小，流場越快達到穩定狀態。

（3）為提高魚雷出管速度，并且保證推進泵在啟動過程中無空泡產生以及內部流場以較快時間運行至穩定狀態，建議以0.2 s啟動時間啟動推進泵。