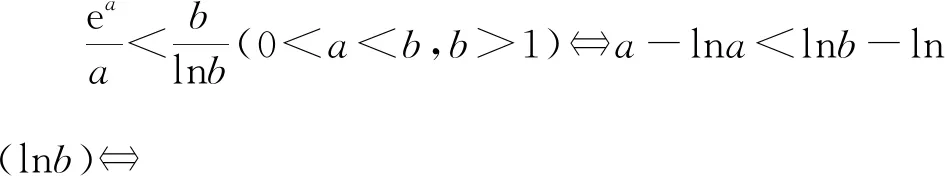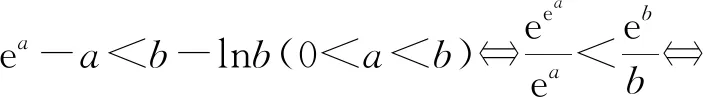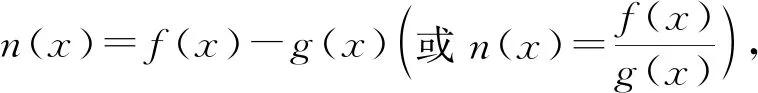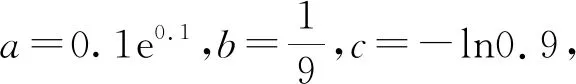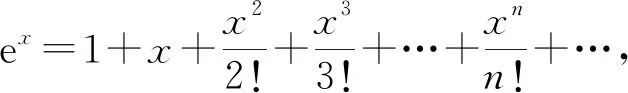指向“通性通法”的一類數式大小比較問題
張隆億
(福建省永春第一中學)
章建躍博士指出,解題教學中注重“通性通法”是一種追求長期利益的有效途徑.其中,“通性”指的是數學概念所蘊含的基本性質,它們是解決問題的關鍵特征.而“通法”則強調利用這些基本性質所提供的思想方法來解決各類問題.在解題教學中,深入理解數學概念的本質和背后的通性,學生不僅能夠解決當前問題,還能夠應用這些通性通法解決更廣泛和復雜的問題,也使他們在數學學習和實際生活中受益終身.
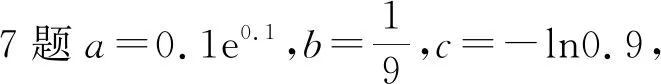
命題手法1 已知方程f(a,b)=0,比較a,b的大小
這類試題以方程f(a,b)=0為條件,比較a,b的大小.一般以選擇題形式進行考查,往往以指數、對數函數和不等式為載體,考查數學抽象、邏輯推理、數學運算等核心數學素養,注重考查思維品質和關鍵能力,具有良好的區分度.將方程f(a,b)=0轉化為m(a)=n(b),觀察方程左右兩邊結構,通過放縮同構為不等式g(a)≤g(b).構造函數y=g(x),結合函數y=g(x)的單調性將不等式g(a)≤g(b)轉化為a,b的大小,從而達到化繁為簡的目的.
【例1】(2020新課標Ⅰ理科12題)若2a+log2a=4b+2log4b,則
( )
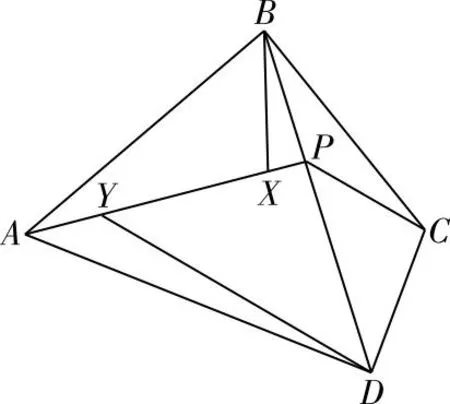
A.a>2bB.a<2bC.a>b2D.a 【分析一】方程2a+log2a=4b+2log4b左右兩邊式子結構比較相近,結合選項比較a與b2,2b的大小,變形為2a+log2a=22b+log2b<22b+log22b,不等式兩邊的結構相同,構造函數f(x)=2x+log2x,所以不等式可化為f(a) 【評析】本解法將方程2a+log2a=4b+2log4b轉化為2a+log2a=22b+log2b,觀察方程左右兩邊結構,通過放縮同構為不等式2a+log2a=22b+log2b<22b+log22b.構造函數f(x)=2x+log2x,結合函數y=f(x)的單調性將不等式f(a) 【分析二】設t=2b,則方程2a+log2a=4b+2log4b可化為2a+log2a=2t+log2t-1.構造函數f(t)=2t+log2t-1-2a-log2a,則函數y=f(t)在(0,+∞)上為增函數且有零點t=2b.由f(a)=-1<0,f(2a)=2a(2a-1)>0得a<2b<2a,所以b 【評析】本解法將方程f(a,b)=0轉化為含參數t的方程g(t)=0,構造函數y=g(t),則函數y=g(t)有零點t,結合函數y=g(t)的單調性及零點存在定理確定零點的范圍,從而得到零點t=2b與a的大小關系,從而達到化繁為簡的目的. 命題手法2 已知不等式f(a,b)<0,比較a,b的大小 這類試題以方程f(a,b)<0條件,常將變量a,b分離,同構為g(a) ( ) (1)積型aea (3)和差型ea+a 命題手法3 已知不能直接比較大小的確定常數a,b,c,比較a,b,c的大小 ( ) A.a C.c 【評析】本題是三個不能直接比較大小的含指數、對數的確定常數比較大小的選擇題.解法中挖掘出了公共的常量0.1,將三個數轉化為三個函數值,再通過兩邊取對數得到lna-lnb=0.1+ln(1-0.1),構造函數f(x)=x+ln(1-x),x∈(0,0.1],結合函數f(x)=x+ln(1-x),x∈(0,0.1]的單調性,得到f(0.1) 在教學中,我們經常發現,學過和練過的知識在考試中卻無法取得高分.究其原因:我們在講練習時注重具體題型和技巧,卻忽視了培養學生的“通性通法”,導致學生的學科素養沒有得到有效提升,造成教與學脫鉤,教學效率低下.因此,我們應該遵循“課程標準”,重視基礎知識、基本技能的掌握途徑,提升數學核心素養.這樣的改進不僅能夠帶來眼前的利益,也能為學生的長遠發展打下堅實的基礎.數學競賽亦如此,2022年全國高中數學聯合競賽加試試題(A卷)第一題:如圖,在凸四邊形ABCD中,∠ABC=∠ADC=90°,對角線BD上一點P滿足∠APB=2∠CPD,線段AP上兩點X,Y滿足∠AXB=2∠ADB,∠AYD=2∠ABD.證明:BD=2XY. 這道平面幾何題對學生的要求體現了近年來數學競賽對平面幾何能力的要求,強調了基本知識、定理和方法的應用.然而,賽后反饋顯示,許多學生在面對條件“∠AXB=2∠ADB,∠AYD=2∠ABD”以及“∠APB=2∠CPD”時感到束手無策,不知所措.這提醒我們在平時訓練學生時要更加積極地探索解題思路的合理性,盡管存在多種思路與方法,但通性通法應成為首選. 通過對近年來高考和高考模擬中數式比較題的分析,我們可以發現這樣的規律:對數函數模型、三角函數模型等典型函數模型的數式大小比較問題,頻繁出現在各類考試的選擇題中,難度有大有小.雖然形式看起來可能有很多變化,但萬變不離其宗.如果我們能從數式大小比較問題的通性通法入手,深入了解構造函數法適用條件及解題步驟,然后運用函數的單調性,突破數式大小比較解題障礙點.學生通過運用“通性通法”,能夠靈活應用已學知識解決問題,不僅在短期內取得好成績,還能培養數學素養和解題能力,為長期發展打下基礎.此外,我們在教學中不僅要關注一題多解,更需要關注多題一解,注重通性通法,淡化技巧,回歸數學本質,鼓勵學生勤動手、勤反思,多操作、多思考,提升了數學核心素養,感受了“用數學的眼光觀察世界,用數學的思維思考世界,用數學的語言表達世界”的精神內涵.
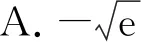

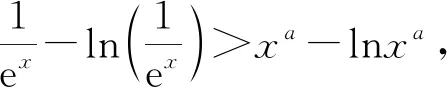
1.利用x=lnex,x=elnx(x>0)進行冪指、冪對轉換同構
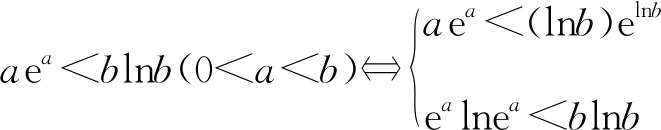
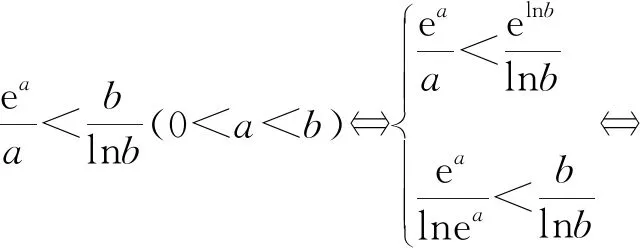
2.對等式、不等式兩邊取指數、對數進行同構