基于SRCKF 算法的多自由度非線性系統(tǒng)動(dòng)載荷識別方法

龔璟淳，陳清華，厲硯磊，王開云

（西南交通大學(xué)軌道交通運(yùn)載系統(tǒng)全國重點(diǎn)實(shí)驗(yàn)室,四川 成都 610031）

準(zhǔn)確快速地識別機(jī)械系統(tǒng)的動(dòng)載荷對系統(tǒng)的振動(dòng)響應(yīng)測量、結(jié)構(gòu)參數(shù)優(yōu)化、疲勞壽命預(yù)測等具有重要意義。對于軌道車輛、飛行器等復(fù)雜非線性系統(tǒng)，直接測量輪軌作用力、飛行器外載荷等十分困難。因此，研究識別精度高、響應(yīng)速度快的動(dòng)載荷的間接識別方法具有重要的工程實(shí)用性。

動(dòng)載荷識別方法主要分為時(shí)域識別法和頻域識別法。頻域識別法經(jīng)過多年發(fā)展已較為成熟，其識別精度高但對噪聲敏感，只適用于穩(wěn)態(tài)動(dòng)載荷和平穩(wěn)隨機(jī)載荷[1]。時(shí)域識別法起步較晚，其基本原理是將系統(tǒng)運(yùn)動(dòng)方程進(jìn)行模態(tài)坐標(biāo)變換，將動(dòng)力方程解耦，再根據(jù)卷積后的激勵(lì)與系統(tǒng)響應(yīng)的關(guān)系識別出動(dòng)載荷。武江凱等[2]以二次多項(xiàng)式為基函數(shù)，基于Duhamel 積分推導(dǎo)建立了一種針對單自由度振動(dòng)系統(tǒng)的動(dòng)態(tài)載荷識別方法。樊懿葳等[3]在此基礎(chǔ)上通過模態(tài)坐標(biāo)變換法，將多自由度振動(dòng)系統(tǒng)運(yùn)動(dòng)方程解耦，建立了一種以系統(tǒng)加速度為輸入的多自由度振動(dòng)系統(tǒng)動(dòng)載荷時(shí)域識別方法。以上研究均針對線性系統(tǒng)，難以解決非線性系統(tǒng)的載荷識別問題。

卡爾曼濾波是一種結(jié)合模型先驗(yàn)估計(jì)和測量更新的狀態(tài)估計(jì)算法[4-6]。馬也馳等[7]基于卡爾曼濾波方法和最小方差估計(jì)方法，分別建立了以系統(tǒng)位移和加速度為輸入?yún)?shù)的激振力時(shí)域識別方法。Impraimakis 等[8]設(shè)計(jì)了一個(gè)新型無跡卡爾曼濾波器，實(shí)現(xiàn)了非線性系統(tǒng)所有動(dòng)態(tài)狀態(tài)參數(shù)和輸入?yún)?shù)的實(shí)時(shí)聯(lián)合識別。LIU 等[9]基于擴(kuò)展卡爾曼濾波方法，引入主成分分析（PCA）方法變換多維區(qū)間模型，建立了一種用于線性系統(tǒng)動(dòng)載荷識別的動(dòng)態(tài)力重構(gòu)方法。許多研究[10-12]表明，卡爾曼濾波在載荷識別方面具有很強(qiáng)的實(shí)用性。

平方根容積卡爾曼濾波（SRCKF）[13]是一種基于三階球面徑向容積準(zhǔn)則和平方根濾波的改進(jìn)卡爾曼濾波算法。穆靜等[14]應(yīng)用SRCKF 算法對未知彈道系數(shù)的再入彈道目標(biāo)實(shí)現(xiàn)了快速精確的狀態(tài)估計(jì)。肖仁鑫等[15]基于SRCKF 算法結(jié)合遺忘因子，對電池荷電狀態(tài)進(jìn)行在線辨識。以上研究表明，在非線性過程問題中，平方根容積卡爾曼濾波算法有較好的估計(jì)效果。

針對鐵道車輛車鉤等存在非線性剛度阻尼的單一維度、多自由度系統(tǒng)的外部動(dòng)載荷，本文提出了一種基于SRCKF 算法的多自由度非線性系統(tǒng)動(dòng)載荷識別方法，通過建立包含動(dòng)載荷的系統(tǒng)狀態(tài)非線性遞推函數(shù)，結(jié)合平方根容積卡爾曼濾波算法和系統(tǒng)各部件振動(dòng)加速度響應(yīng)來更新估計(jì)動(dòng)載荷。為驗(yàn)證算法可行性，本文以二自由度非線性彈簧阻尼振子系統(tǒng)為例分析了該算法對隨機(jī)激勵(lì)和組合諧波激勵(lì)的識別效果。

1 非線性系統(tǒng)建模與識別算法

1.1 二自由度非線性彈簧阻尼模型

以具有剛度非線性和阻尼非線性的彈簧振子串聯(lián)振動(dòng)系統(tǒng)為研究對象，如圖1 所示，系統(tǒng)的振動(dòng)方程為

式中：M為系統(tǒng)質(zhì)量矩陣；C為系統(tǒng)阻尼矩陣；K為系統(tǒng)剛度矩陣；X、和分別為系統(tǒng)的位移、速度和加速度向量；F為系統(tǒng)動(dòng)載荷。

在剛度非線性系統(tǒng)中，k1具有非線性特性，如圖2 所示，彈簧力計(jì)算公式為

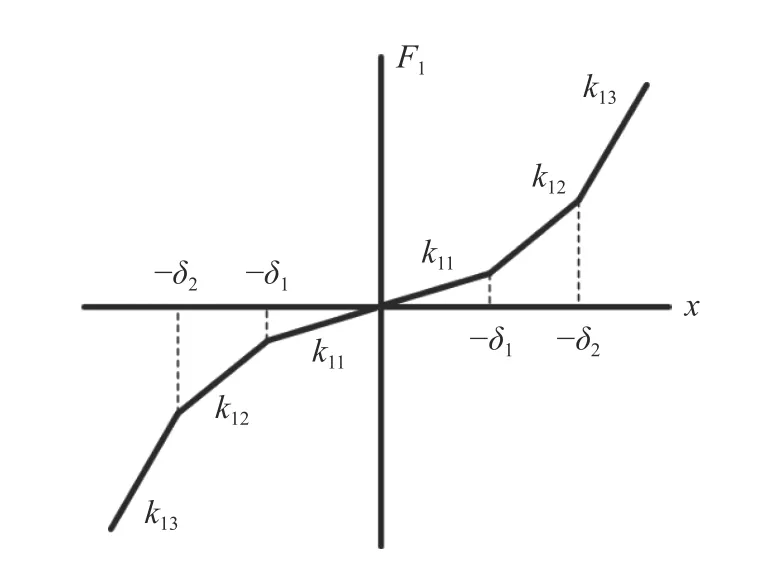
圖2 非線性剛度特性示意圖Fig.2 Diagram of nonlinear stiffness characteristics

式中：k1i（i=1～3）為剛度系數(shù)；b為相對位移；δi（i=1～2）為間斷點(diǎn)對應(yīng)位移值；sign()表示對取變量的正負(fù)號。

在阻尼非線性系統(tǒng)中，c1具有非線性特性，如圖3 所示，阻尼力計(jì)算公式為

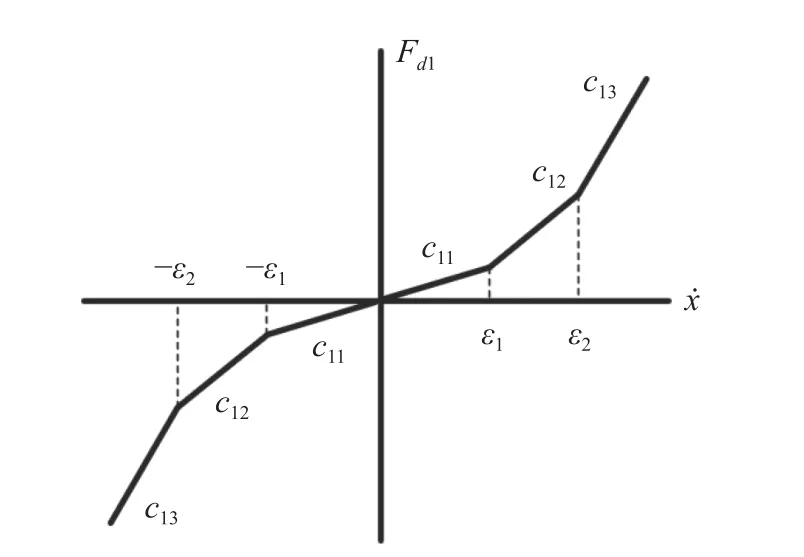
圖3 非線性阻尼特性示意圖Fig.3 Diagram of nonlinear damping characteristics

式中：c1i（i=1～3）為阻尼系數(shù)；為相對速度；εi（i=1～2）為間斷點(diǎn)對應(yīng)速度值。

1.2 SRCKF 算法識別原理

對于上述二自由度系統(tǒng)模型，其狀態(tài)變量為

式中：z1、z2分別為質(zhì)量塊m1、m2的垂向位移；、分別為質(zhì)量塊m1、m2的垂向速度。

將振動(dòng)系統(tǒng)所受動(dòng)載荷看作系統(tǒng)內(nèi)在狀態(tài)，將狀態(tài)變量擴(kuò)充為

此時(shí)振動(dòng)系統(tǒng)的狀態(tài)空間方程為：

對于系統(tǒng)的位移、速度和加速度響應(yīng)，在實(shí)際工程應(yīng)用中，加速度響應(yīng)相比位移和速度響應(yīng)更易測量，因此，選擇系統(tǒng)中各部件振動(dòng)加速度作為系統(tǒng)觀測量，為

實(shí)際上傳感器測量的數(shù)據(jù)為離散采樣，因此，將系統(tǒng)狀態(tài)方程離散化。根據(jù)固定積分步長采用四階龍格庫塔法對遞推式進(jìn)行時(shí)域積分迭代更新。

式中：xk∈Rnx為系統(tǒng)狀態(tài)變量；zk為觀測量。過程噪聲wk-1和量測噪聲vk為相互獨(dú)立的高斯分布，即wk-1～N(0,Qk-1)，vk-1～N(0,Rk-1)。

結(jié)合以上公式，采用平方根容積卡爾曼濾波算法對系統(tǒng)動(dòng)載荷的識別流程如圖4 所示。核心步驟是根據(jù)識別的第k-1 步的狀態(tài)變量xk-1遞推出第k步的狀態(tài)變量xk識別值。首先對狀態(tài)變量x0和誤差協(xié)方差矩陣P0進(jìn)行初始化，給定過程噪聲矩陣Q和測量噪聲矩陣R的初始值。然后進(jìn)行時(shí)間更新，通過xk-1計(jì)算容積點(diǎn)Xj,k-1，將容積點(diǎn)代入非線性狀態(tài)方程計(jì)算傳播后的容積點(diǎn)，再計(jì)算k時(shí)刻狀態(tài)量預(yù)測值和誤差協(xié)方差矩陣的平方根，為：

圖4 SRCKF 算法流程圖Fig.4 Algorithm flow chart of SRCKF

式中：Sk-1為Pk喬列斯基分解后得到的上三角矩陣；ξj（j=1～m）為容積點(diǎn)集；Tria()表示對矩陣進(jìn)行三角化，獲得矩陣的方陣；為中心加權(quán)矩陣，為

接著進(jìn)行測量更新，根據(jù)k時(shí)刻狀態(tài)量預(yù)測值和誤差協(xié)方差矩陣的平方根計(jì)算容積點(diǎn)Xj,k，將Xj,k代入測量方程進(jìn)行傳播，得到傳播后的容積點(diǎn)Zj,k，再計(jì)算k時(shí)刻的測量量預(yù)測值、測量誤差協(xié)方差矩陣的平方根和誤差協(xié)方差矩陣Pk，為：

式中SR,k為Rk的平方根。γk、χk定義為：

最后，計(jì)算卡爾曼增益Wk、狀態(tài)量估計(jì)值xk和誤差協(xié)方差矩陣平方根估計(jì)值Sk，完成一次狀態(tài)更新。

通過連續(xù)的狀態(tài)更新過程，就能實(shí)現(xiàn)振動(dòng)系統(tǒng)動(dòng)載荷的實(shí)時(shí)識別。

2 算法驗(yàn)證

以圖1 所示的二自由度非線性振動(dòng)系統(tǒng)為例進(jìn)行驗(yàn)證。系統(tǒng)的各部件質(zhì)量為m1=4 kg，m2=8 kg，剛度非線性系統(tǒng)參數(shù)如表1 所示，阻尼非線性系統(tǒng)參數(shù)如表2 所示。

表1 剛度非線性系統(tǒng)參數(shù)Tab.1 Stiffness parameters of nonlinear system

表2 阻尼非線性系統(tǒng)參數(shù)Tab.2 Damping parameters of nonlinear system

采用相關(guān)系數(shù)和均方根誤差值對識別結(jié)果進(jìn)行判斷。相關(guān)系數(shù)能描述識別結(jié)果的變化趨勢，均方根誤差值側(cè)重于衡量真實(shí)值與識別值之間的差異。均方根誤差計(jì)算公式為

式中：y為真實(shí)值；為預(yù)測值；m為觀測次數(shù)。

2.1 隨機(jī)激勵(lì)識別

圖5 為隨機(jī)激勵(lì)作用下剛度非線性系統(tǒng)動(dòng)載荷識別的時(shí)域圖、頻域圖和均方根誤差圖。可以看出，系統(tǒng)動(dòng)載荷的識別曲線和仿真輸入曲線十分接近，識別曲線和動(dòng)載荷曲線的相關(guān)系數(shù)達(dá)0.997。由圖5（b）可知，在動(dòng)載荷高于0.8 Hz 頻段時(shí)識別結(jié)果十分準(zhǔn)確，低于0.8 Hz 頻段識別結(jié)果存在較小誤差。由圖5（c）可知，在識別過程開始時(shí)，均方根誤差達(dá)到最大值17.553 N，隨后快速減小并穩(wěn)定在2.052 N 以下。

圖5 剛度非線性系統(tǒng)隨機(jī)激勵(lì)識別結(jié)果圖Fig.5 Results of random excitation identification for nonlinear stiffness systems

圖6 為隨機(jī)激勵(lì)作用下阻尼非線性系統(tǒng)動(dòng)載荷識別的時(shí)域圖、頻域圖和均方根誤差圖。從圖6（a）可以看出，識別曲線和真實(shí)曲線大致重合，相關(guān)系數(shù)達(dá)0.999。圖6（b）的頻域結(jié)果表明，在各個(gè)頻段識別效果都很好。圖6（c）顯示均方根誤差在識別過程開始時(shí)出現(xiàn)最大值1.258 N，隨后急劇減小并穩(wěn)定在0.033 N 以下。

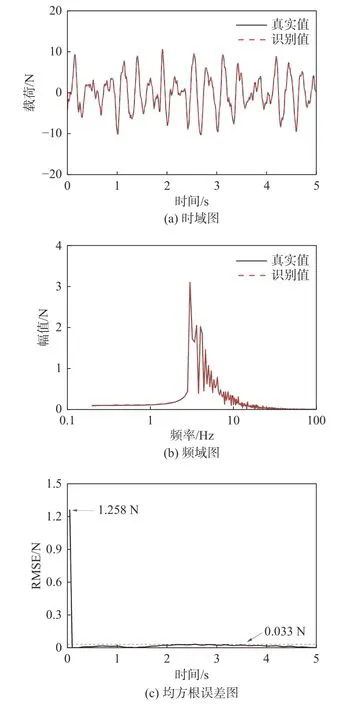
圖6 阻尼非線性系統(tǒng)隨機(jī)激勵(lì)識別結(jié)果圖Fig.6 Results of random excitation identification for nonlinear damping systems

2.2 組合諧波激勵(lì)載荷識別

圖7 為對剛度非線性系統(tǒng)施加頻率為1、2、3、5 和7 Hz 的組合諧波激勵(lì)時(shí)的動(dòng)載荷識別結(jié)果。圖7（a）的動(dòng)載荷時(shí)域識別圖表明，識別曲線和動(dòng)載荷曲線變化趨勢一致，相關(guān)系數(shù)為0.997。圖7（b）的頻域動(dòng)載荷曲線和識別曲線的對比可知，在頻率大于0.8 Hz 時(shí)識別效果較好，在小于0.8 Hz 時(shí)，隨著頻率的減小，識別誤差逐漸增大。由圖7（c）的系統(tǒng)動(dòng)載荷曲線和識別曲線的均方根誤差可知，識別過程中均方根誤差存在一定波動(dòng)，最大值為0.866 N，均方根誤差整體處于較低的水平。

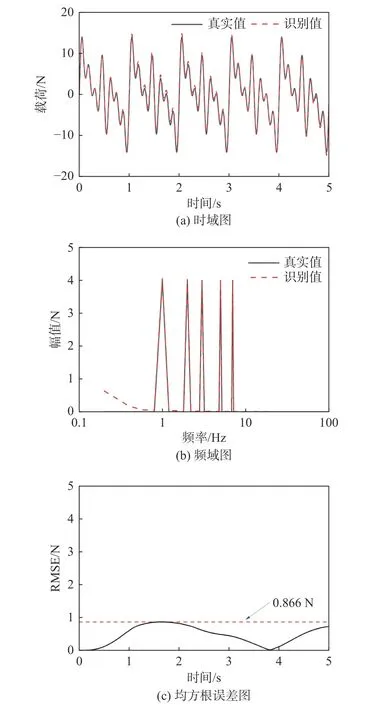
圖7 剛度非線性組合諧波激勵(lì)識別結(jié)果圖Fig.7 Results of harmonic excitation identification for nonlinear stiffness systems

圖8 為對阻尼非線性系統(tǒng)施加頻率為1、2、3、5 和7 Hz 的組合諧波激勵(lì)時(shí)的動(dòng)載荷識別結(jié)果。圖8（a）表明，識別曲線和真實(shí)曲線基本重合，二者的相關(guān)系數(shù)達(dá)0.999。由圖8（b）可以看出，在頻率大于0.8 Hz 時(shí)識別曲線和動(dòng)載荷曲線基本重合，在頻率小于0.8 Hz 時(shí)識別幅值偏大。從圖8（c）可以看出，識別值與真實(shí)值的均方根誤差隨識別過程不斷變化，其最大值為0.234 N，整體收斂在一個(gè)較低的水平。

圖8 阻尼非線性系統(tǒng)組合諧波激勵(lì)識別結(jié)果圖Fig.8 Results of harmonic excitation identification for nonlinear damping systems

3 結(jié)論

本文基于SRCKF 算法提出了一種多自由度非線性振動(dòng)系統(tǒng)動(dòng)載荷的識別方法，并通過二自由度的剛度非線性和阻尼非線性的彈簧阻尼振子系統(tǒng)對算法進(jìn)行了驗(yàn)證。

1）在剛度非線性系統(tǒng)上施加隨機(jī)激勵(lì)和組合諧波激勵(lì)時(shí)，識別曲線與輸入載荷曲線相關(guān)系數(shù)均達(dá)0.997。在阻尼非線性系統(tǒng)上施加隨機(jī)激勵(lì)和組合諧波激勵(lì)時(shí)，識別曲線與輸入載荷曲線相關(guān)系數(shù)均達(dá)0.999。

2）在頻率大于0.8 Hz 的頻段，識別結(jié)果與輸入載荷基本吻合。在小于0.8 Hz 的低頻段，識別結(jié)果存在一定誤差。

3）對于隨機(jī)激勵(lì)，識別結(jié)果的均方根誤差的最大值出現(xiàn)在識別初始時(shí)，隨著識別過程的進(jìn)行，識別的誤差逐步收斂至較低的水平；對于組合諧波激勵(lì)，識別結(jié)果的均方根誤差存在小幅波動(dòng)，整體處于較低水平。