中低速磁浮列車走行部迫導向機構轉向特性研究

張 碩，李良杰，代瑞珍，王 巖

（1.中車唐山機車車輛有限公司，高級工程師，河北 唐山 063035；2.河北省軌道車輛轉向架技術創新中心，高級工程師，河北 唐山 063000）

0 引言

2010年以來，多種形式在中國城市軌道交通領域得到迅猛發展，與此，中低速磁浮列車也實現了從無到有的突破性成就［1］，磁浮列車不同于其他軌道交通車輛，不受傳統輪軌關系的限制，具有振動噪聲低、運行平穩、曲線通過能力強、爬坡能力強等優點，越來越受到青睞［2-3］。現有運營的磁浮車輛均采用五模塊懸浮架結構，為實現前后懸浮架的聯動關系從而提高車輛曲線通過能力，故在車體與懸浮架之間設置機械式的迫導向機構，以增加車體的復位能力。但現有的五模塊懸浮架在迫導向機構作用下進入曲線時無法完成所有懸浮架實現最佳角度的轉向，懸浮架會出現橫向滑橇與F 軌接觸導致磨損嚴重、迫導向機構相關部件異常受力的問題，導致磁浮列車的運維成本的增加。

因此，有必要開展中低速磁浮列車走行部迫導向機構轉向特性研究。

1 迫導向結構主要組成

由于單節車輛采用五懸浮架結構，因此在每輛車下布置迫導向機構2套，如圖1所示，分別布置在第1、2懸浮架和第4、5懸浮架之間，連接端部滑臺和中間滑臺，縱向對稱布置，主要由長T臂、短T臂、T臂支座、T臂連桿以及導向桿等組成。

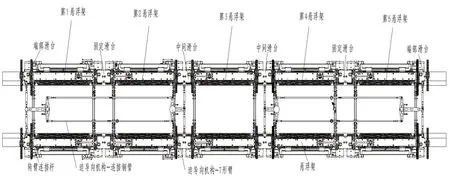
圖1 中低速磁浮列車懸浮架走行部俯視圖

長T臂和短T臂通過T臂支座安裝在車體上，T臂支座中設置有轉軸和軸承，使得T 臂可繞垂直與車體地板面的軸線旋轉。長T臂和短T臂之間通過T臂連桿連接組成平行四邊形機構，由此可使長、短T臂的轉角相等，從而在兩者之間傳遞運動關系。T 臂通過四根導向桿與滑臺連接，從而可將車體的橫向載荷傳遞到各個橫向滑臺上，再通過空簧傳遞到懸浮模塊上，迫導向機構組成如圖2所示。

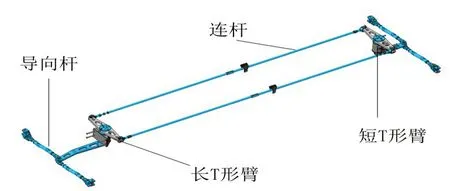
圖2 迫導向機構組成

2 理論計算

根據迫導向機構的工作原理，迫導向機構需要通過計算確定的尺寸參數主要包括：長短T 臂尾臂長度比例、導向桿受力、T臂轉軸受力。

為進一步分析迫導向機構在清遠線運動過程中的運動關系及受力，計算時對迫導向機構、滑臺等主要構件進行簡化，建立幾何參數模型，如圖3所示。

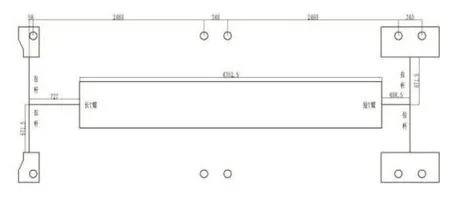
圖3 迫導向機構幾何模型

2.1 運動學計算

建立如圖4所示的直角坐標系。

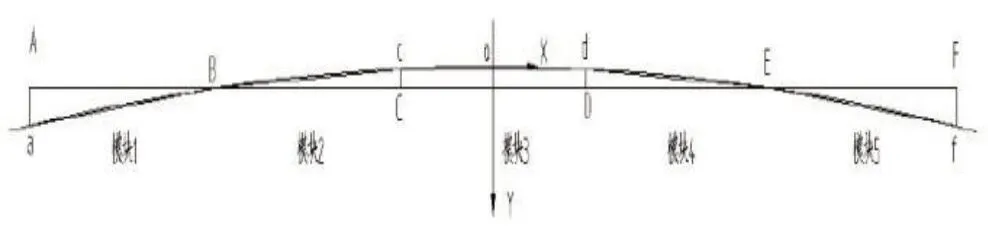
圖4 車輛通過平曲線簡圖

其中，直線AF表示車體縱向中心線，A、B、C、D、E、F 分別表示1-6 位兩側滑臺中心連線中點，曲線表示軌道中心線，a、c、d、f 表示模塊在軌道上的投影。由圖可知具體參數定義如下：

平曲線半徑為R。

由幾何關系可得，端部滑臺橫移量L1：

中間滑臺橫移量L2：

根據公式計算不同軌道半徑下端部滑臺和中間滑臺橫移量如下表1所示。

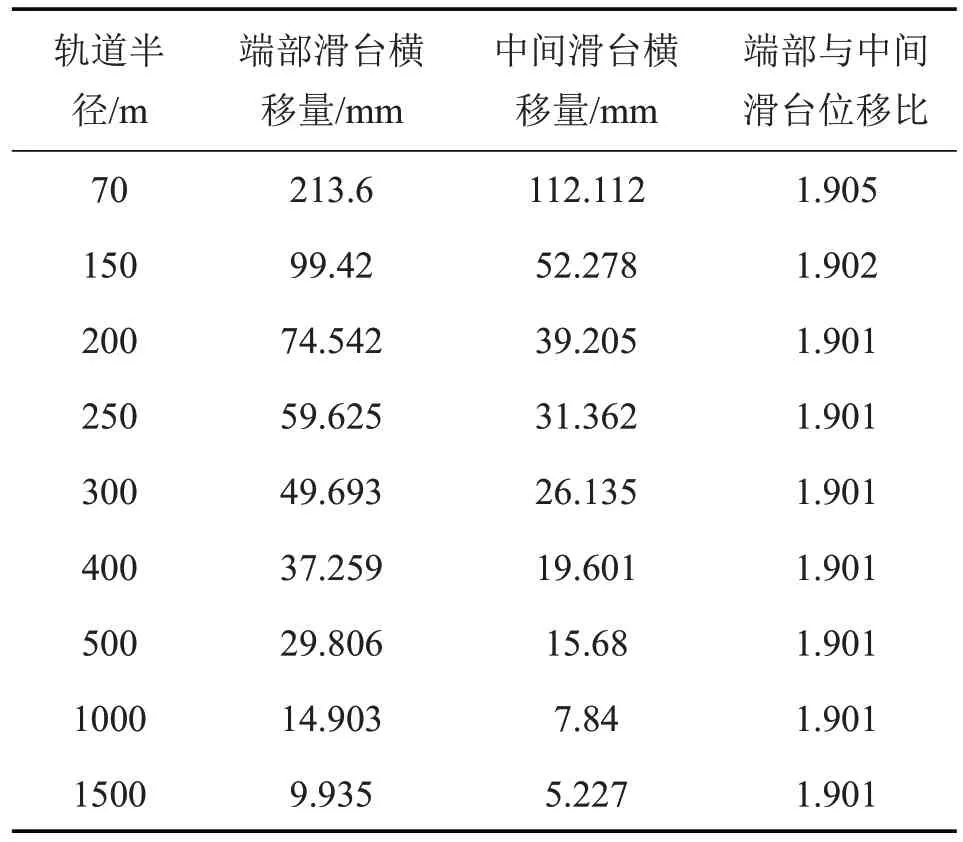
表1 不同曲線半徑對應滑臺橫向位移

從上表可以看出，不同水平曲線半徑下，端部滑臺與中間滑臺的橫向位移均不相同，且位移比也在變化，根據迫導向機構工作原理，這也意味著長短T臂尾臂長度比也應隨之變化，才能確保各懸浮模塊更好地跟蹤軌道曲線，但是實際設計過程中須確定一個固定的長短T臂尾臂長度比。

根據公式（1）和公式（2），當R遠大于a和a1時，可以得到

將模塊1長度（2688mm）和模塊2長度（2800mm）帶入公式（3），得到：

根據以上計算，將長短T 臂尾臂長度比設計為1.9，并在后續仿真驗證時進行優化。

2.2 受力計算

2.2.1 整車橫向受力分析 磁浮車輛勻速在圓曲線半徑上運動時，受力主要包括車輛重量、離心力F離、電磁鐵產生的懸浮力F懸和導向力F導，受力模型如圖5所示。

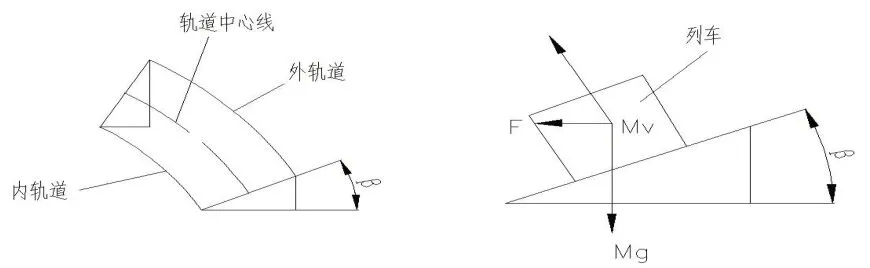
圖5 整車彎道受力分析圖

根據受力可得：

其中，V—曲線通過速度，M—車輛質量，β—軌道橫坡角。

根據清遠線線路條件可到：

車場線：半徑70m，速度10km/h，無橫坡角，車輛為空載工況。

最大超高平曲線：最大橫坡角4.63°，車輛為滿載工況。

2.2.2 車輛平曲線靜浮橫向受力分析 由于磁浮車輛導向力傳遞路徑有兩條，在靜浮狀態下，導向力分配關系并不確定，因此在設計時，須考慮導向力分別從兩條路徑獨立傳遞的極端工況。

根據公式（5）和（6）得到T臂受力：

上述受力將作為迫導向機構設計的載荷條件。

2.2.3 超速進入緩和曲線受力分析 根據清遠線線路條件可知，車輛長度15.7m，橫坡角變化為0.074°，超速20%通過，平曲線超高150mm。

導向力需求為：

由計算可得，在超速20%通過緩和曲線時，導向力需求相當于重力分量的0.57，沒有超過圓曲線靜浮工況需要的導向力。

3 仿真計算

根據計算結果，對迫導向機構三維模型進行優化，并將其主要部件進行建模。模型如圖6所示。

圖6 迫導向機構建模

為提高計算效率，根據清遠線線路條件，建立一條包括清遠線所有惡劣線路中最惡劣線路的條件，如圖7所示。

圖7 最惡劣路況復合線路模型

3.1 長短T臂臂長比對轉向特性影響

計算時，按照設計車速通過復合路線時各懸浮點橫向位移變化情況。T臂臂長比分別選用1.9、1.8、1.7，得到如圖8-圖10的仿真結果。

圖8 不同臂長比下橫向位移變化

（1）橫向位移變化對比

比較圖8（a-c）得知，T 臂比不僅影響連接導向桿的懸浮點的橫向位移，也改變了固定滑臺對應懸浮點的橫向位移，T 臂比為1.8 時，所懸浮點橫向位移分布范圍相對較小，且更為對稱。

（2）受力對比

比較圖9和圖10得知，T臂比取為理論值1.9時，在圓曲線上導向桿受力減小，說明此時導向桿對應的懸浮點橫向偏移減小。同時可以發現T臂比為1.8時，固定滑臺導向力更為對稱和均勻分布；為1.7時，則會導致固定滑臺導向力向負值方向偏移。

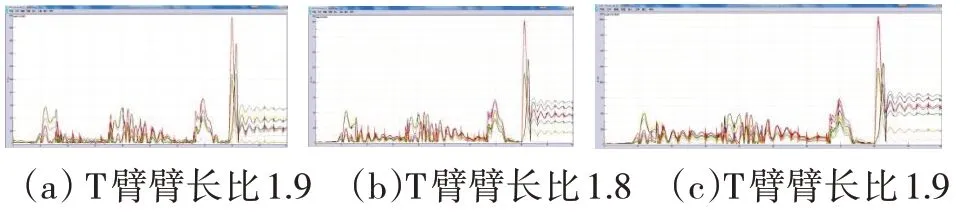
圖9 不同臂長比下導向桿受力

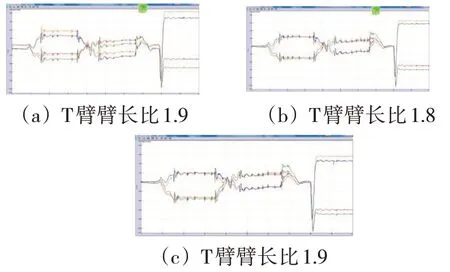
圖10 不同臂長比下固定滑臺受力

3.2 導向桿夾角比對轉向架特性影響

導向桿夾角分別設置為161.2°和180°（即滑臺導向桿鉸點長T臂尾臂導向桿鉸點三點共線），計算結果如圖11所示。

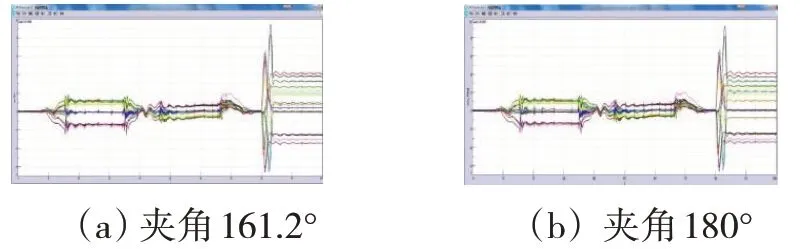
圖11 不同導向桿夾角導向桿受力

從上圖中可以看出，導向桿尖角并不能減小固定滑臺處的電磁鐵橫移量。考慮到工程化實現的建議性，可以取消導向桿夾角。

3.3 滑臺橫向位移仿真驗證

根據設計速度開展運動學仿真分析，得到如圖12的滑臺橫向位移變化曲線。

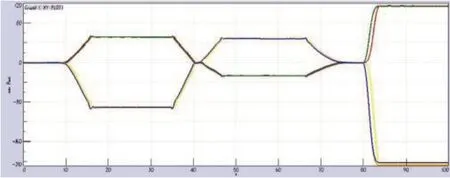
圖12 滑臺橫向位移變化曲線

從上圖可以看出，滑臺在不同半徑圓曲線上的橫向位移仿真結果與計算結果吻合較好，誤差小于3%，能夠滿足工程設計計算的需要。

4 總結

本文介紹了中低速磁浮列車特有的迫導向機構的組成和工作原理，并對主要參數進行了理論計算，在此基礎上開展仿真計算，仿真比較不同迫導向機構設計方案的轉向特性，并優化其機構設計。得到以下結論：

根據中低速磁浮列車通過平曲線的工作原理，采用折線擬合圓弧的方式推導得到各滑臺橫向位移量，并通過運動仿真驗證了理論計算的準確性。

推導得到長、短T臂尾臂長度比的計算公式，計算得到T 臂比理論值為1.9，并通過運動學仿真，將T臂比優化為1.8。利用桿系運動的位姿關系，推導得到T臂導向桿夾角理論值為161.2°，并根據仿真計算結果，在清遠磁浮旅游專線車輛中取消了夾角，優化后的迫導向機構已經裝車并通過試驗驗證，轉向性能優異。