基于灰色回歸模型廣州市果蔬類生鮮農產品冷鏈物流需求預測

劉子玲，謝如鶴*，廖晶，何佳雯，羅湖橋

綠色包裝與循環經濟

基于灰色回歸模型廣州市果蔬類生鮮農產品冷鏈物流需求預測

劉子玲1，謝如鶴1*，廖晶2，何佳雯1，羅湖橋3

（1.廣州大學，廣州 510006；2.廣州番禺職業技術學院，廣州 511483； 3.廣東亞太經濟指數研究中心，廣州 510040）

通過對不同預測方法的誤差進行對比研究，選取預測精度較高的方法，促進部門科學化決策。從農產品供給、社會經濟水平、冷鏈物流保障、居民規模與消費能力四大維度選取15個指標來構建影響因素指標體系，對影響因素與冷鏈物流需求進行灰色關聯度分析。采用GM（1，1）、GM（1，6）與主成分-多元回歸線性模型對果蔬類生鮮農產品冷鏈物流需求進行預測。GM（1，1）預測模型、GM（1，6）預測模型、主成分-多元回歸線性預測模型的預測誤差分別為2.97%、1.70%、2.53%。GM（1，6）預測模型預測精度最高，該模型適用于中短期的冷鏈物流需求預測，具有較高的應用價值。

果蔬類生鮮農產品；灰色預測模型；主成分-多元回歸線性；需求預測

隨著經濟的發展，生活水平的不斷提高，人們越來越注重生活質量，飲食結構隨之發生變化，對果蔬類生鮮農產品的需求量不斷增加。果蔬類生鮮農產品是人體所需營養元素的重要來源，包含維生素、礦物質、膳食纖維等營養物質[1]。廣東作為農業大省，2022年全省水果產量約為1 881萬t，同比增長3%。全省蔬菜總產量約3 992萬t，同比增長了4%[2]。雖然生鮮農產品每年產量都保持上升趨勢，但是果蔬冷鏈物流仍存在流通率低、腐損成本高等問題。在新冠疫情的影響下，消費者對生鮮農產品需求顯著增長。準確的生鮮農產品需求預測對合理配置物流資源、實現供需匹配和制定政策具有重要意義。

在需求預測方面，學者們一般采用定性預測或定量預測，定性預測的方法一般包括訪談法、德爾菲法等，定量預測方法包括多元線性回歸、灰色預測模型、BP神經網絡等。從預測結果的精度上看，定量預測優于定性預測，目前大多數學者采用的是定量預測方法。在多元線性回歸模型方面，孟慶龍等[3]采用多元線性回歸模型對蘋果可溶性固形物含量進行預測。Bessler等[4]構建向量自回歸預測模型來預測肉類的需求量。在灰色預測模型方面，文先明等[5]建立GM（1，）模型對湖南省農產品冷鏈物流需求進行預測。周慧等[6]利用GM（1，1）對九江市的水果、蔬菜、肉類等農產品的產量進行預測。Eksoz等[7]采用神經網絡模型和灰色模型來預測短期冷鏈物流需求。Liu等[8]運用灰色模型和灰色-BP神經網絡模型對水產品冷鏈物流需求進行預測。Ma等[9]利用灰色關系來分析各影響因素與物流需求的相關程度。Ren等[10]建立GM（1，）模型來預測農產品冷鏈物流的需求。在BP神經網絡模型方面，徐曉燕等[11]利用BP神經網絡對山東省的物流需求進行預測。劉艷利等[12]利用BP神經網絡對浙江省水產品冷鏈物流需求量進行預測。Huang等[13]采用GM（1，1）模型和BP神經網絡模型對物流需求進行了模擬預測。Yang[14]基于BP神經網絡對港口進出口物流進行了需求預測。He等[15]基于神經網絡算法和灰色預測模型對冷鏈物流需求進行預測。

目前，在預測方法的選擇上，多數學者傾向于采用單一方法，在綜合運用多種方法進行需求預測上還有所欠缺。此外，在指標體系指標選取上，多集中于宏觀經濟指標，指標針對性亟待加強。因此，有必要對預測方法以及指標體系這2個方面進行更加細致的學術探討。基于此，本文以廣州市果蔬類農產品為研究對象，對比分析了GM（1，1）、GM（1，6）、主成分-多元線性回歸分析模型，選取預測精度最高的模型，這有助于更加準確地進行需求預測，合理配置物流資源，實現供需匹配，提高相關主體決策的科學性。此外，考慮到廣州市果蔬類農產品產量大、居民喜食果蔬類農產品等現狀，本文將居民果蔬農產品消費偏好納入到影響因素指標體系之中。該指標體系能更為貼近廣州市的實際情況，具有新穎性與實用性。通過選取精度更高的預測方法以及構建需求指標體系，為果蔬類冷鏈物流需求預測研究提供一定的理論基礎。

1 果蔬類生鮮農產品冷鏈物流需求量影響因素分析

1.1 預測指標

考慮到冷鏈流通率數據獲取較困難，本文從消費端角度出發，用果蔬類生鮮農產品人均消費量乘以居民人口數量作為果蔬類生鮮農產品冷鏈物流需求的預測指標。

1.2 影響因素指標

果蔬類生鮮農產品冷鏈物流需求需綜合考慮多方面影響。結合已有研究及專家訪談，將預測指標劃分為農產品供給、社會經濟水平、冷鏈物流保障、居民規模與消費能力這四大維度，具體指標選取及來源如表1所示。

表1 指標體系

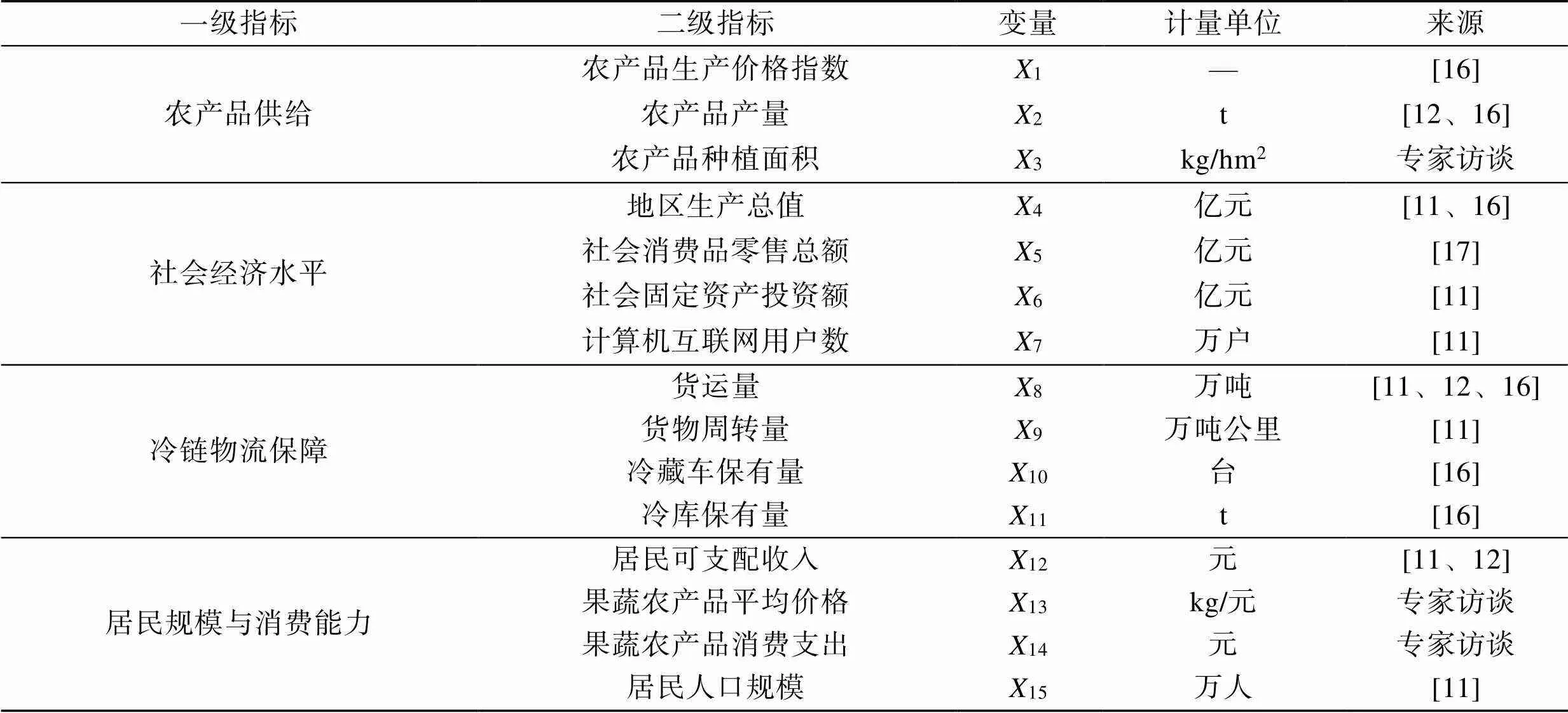
Tab.1 Indicator system

2 模型構建

2.1 灰色關聯度分析

灰色關聯度分析是一種多因素統計分析的方法。具體步驟[18]如下：首先，確立母序列與子序列；其次，對數據進行歸一化處理，接著，計算關聯系數，見式（1）。

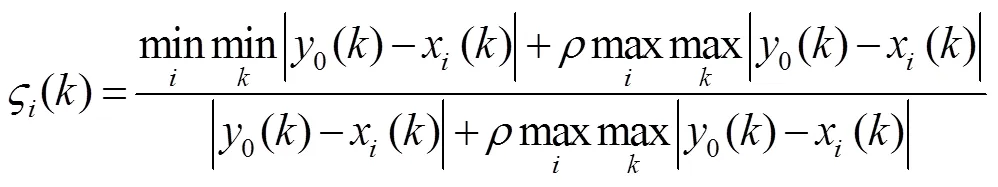
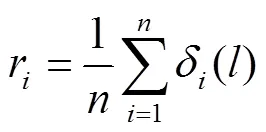
灰色關聯度的取值范圍為[0, 1]，值越大的說明灰色關聯度越大。

2.2 GM（1，1）模型

GM（1，1）是一種時間序列預測的方法，適用于中短期預測，具體預測步驟[18]：首先，將原始數作累加，設原始灰色數據：

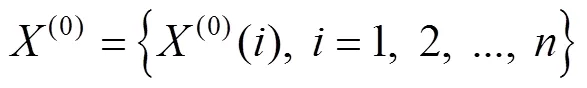
對式（3）進行一次累加得到：

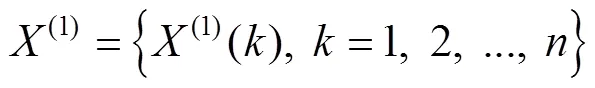
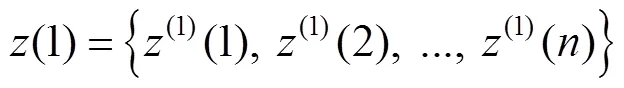
式（6）微分方程的解為：

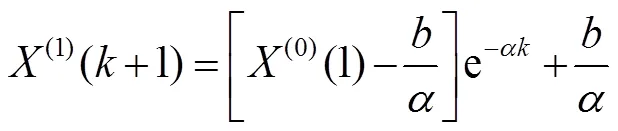
最后預測值可以還原為：

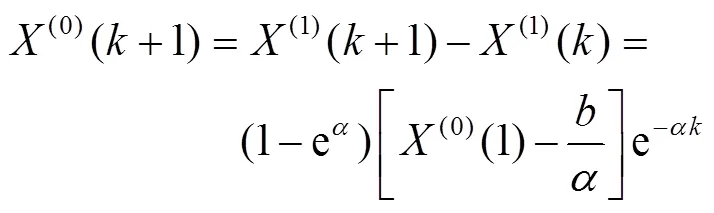
2.3 GM（1，N）模型

GM（1，）模型的預測原理與GM（1，1）類似，不同在于輸入數據變量是個。具體計算過程[16]如下。

首先，對原始數列進行級比檢驗：

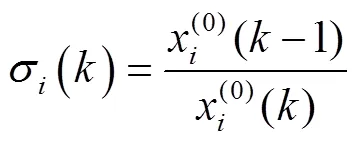
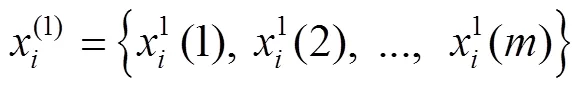
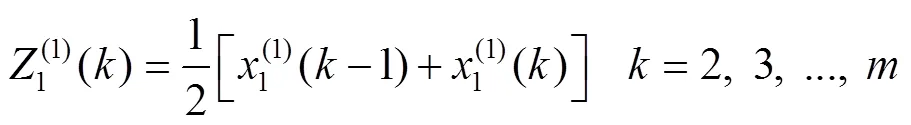
建立微分方程：

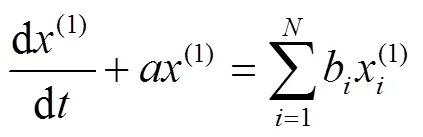
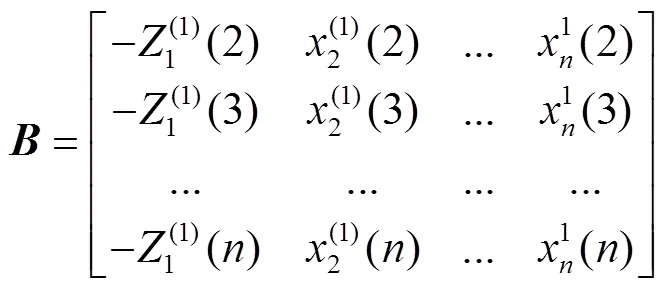
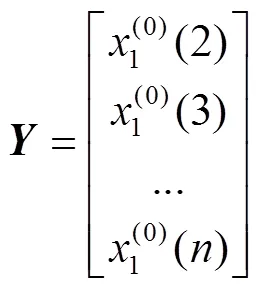
GM（1，）預測模型為：

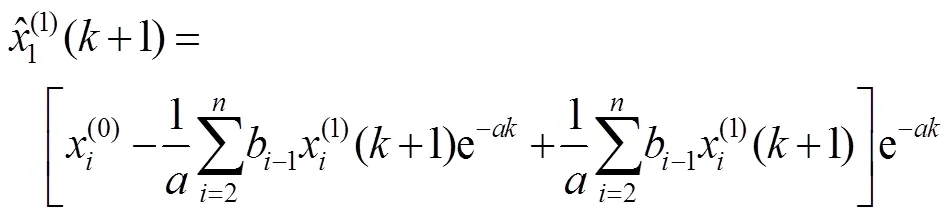
最后累減還原式為：

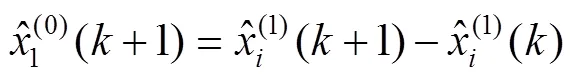
2.4 主成分-多元線性回歸預測模型

2.4.1 主成分分析

主成分分析法是通過恰當的空間變換，使新變量主成分成為原變量的線性組合，并選取少數幾個在原始總信息量中占比較大的主成分來分析事物的一種方法。具體步驟[19]如下：

首先，原始數據標準化：

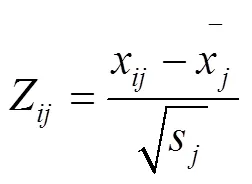
其中，

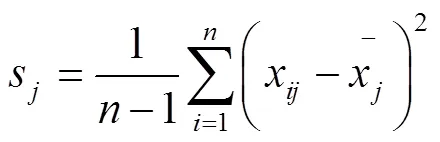
接著，分別計算相關系數矩陣、特征值及特征向量、方差貢獻率。r為原始變量x與x之間的相關系數，計算式為：

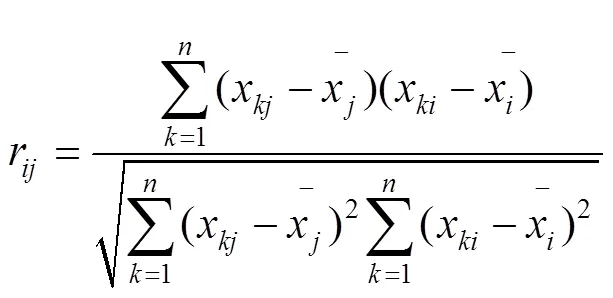
計算相關矩陣的特征值λ，并降序排列，即1≥2≥...≥0；然后，分別求出各個特征值所對應的特征向量。第個主成分y的方差貢獻率為：

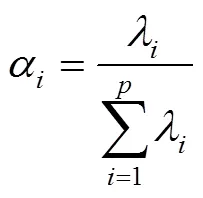
式中：α為第個主成分y在原始總方差的占比。前個主成分1,2, ...,y的累計方差貢獻率()為：

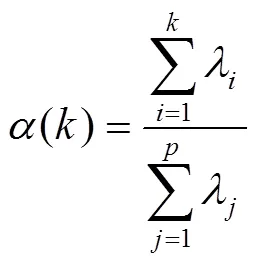
最后，確定主成分提取的個數有2個標準，即選擇特征值大于1的前個主成分；選擇前個主成分的累計貢獻率大于85%。

2.4.2 多元回歸分析

多元線性回歸指對2個及以上自變量與因變量進行相關分析，建立預測模型，見式（23）。

將式（23）進行反標準化，得到：

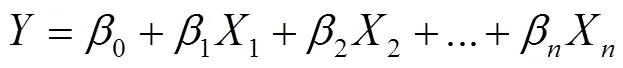
式中：為因變量；X（=1, 2, …,）為自變量；0為常數項；β（=1, 2, …,）為回歸系數。最后需要進行逆標準化計算，從而得到最終的表達式。

3 實證分析

3.1 數據獲取

本文數據來自2010—2022年《廣州市統計年鑒》《中國物流年鑒》等，如表2所示。

利用MATLAB對各影響因素灰色關聯度進行計算，各指標的灰色關聯度分別如下：2為0.942，15為0.937，14為0.927，13為0.914，7為0.885，3為0.879，1為0.877，5為0.870，6為0.846，4為0.845，12為0.842，8為0.792，11為0.773，X9為0.618，10為0.566。關聯度值介于0～1，該值越大表示相關性越強。依照灰色關聯度理論，一般灰色關聯度大于0.6的可以被接受[18]。5個指標中只有10低于0.6，故10需剔除。

3.2 實證分析

3.2.1 GM（1，1）模型分析

通過MATLAB軟件進行計算，2010—2022年的預測結果如圖1所示。

表2 廣州市果蔬類生鮮農產品需求量及影響指標數據

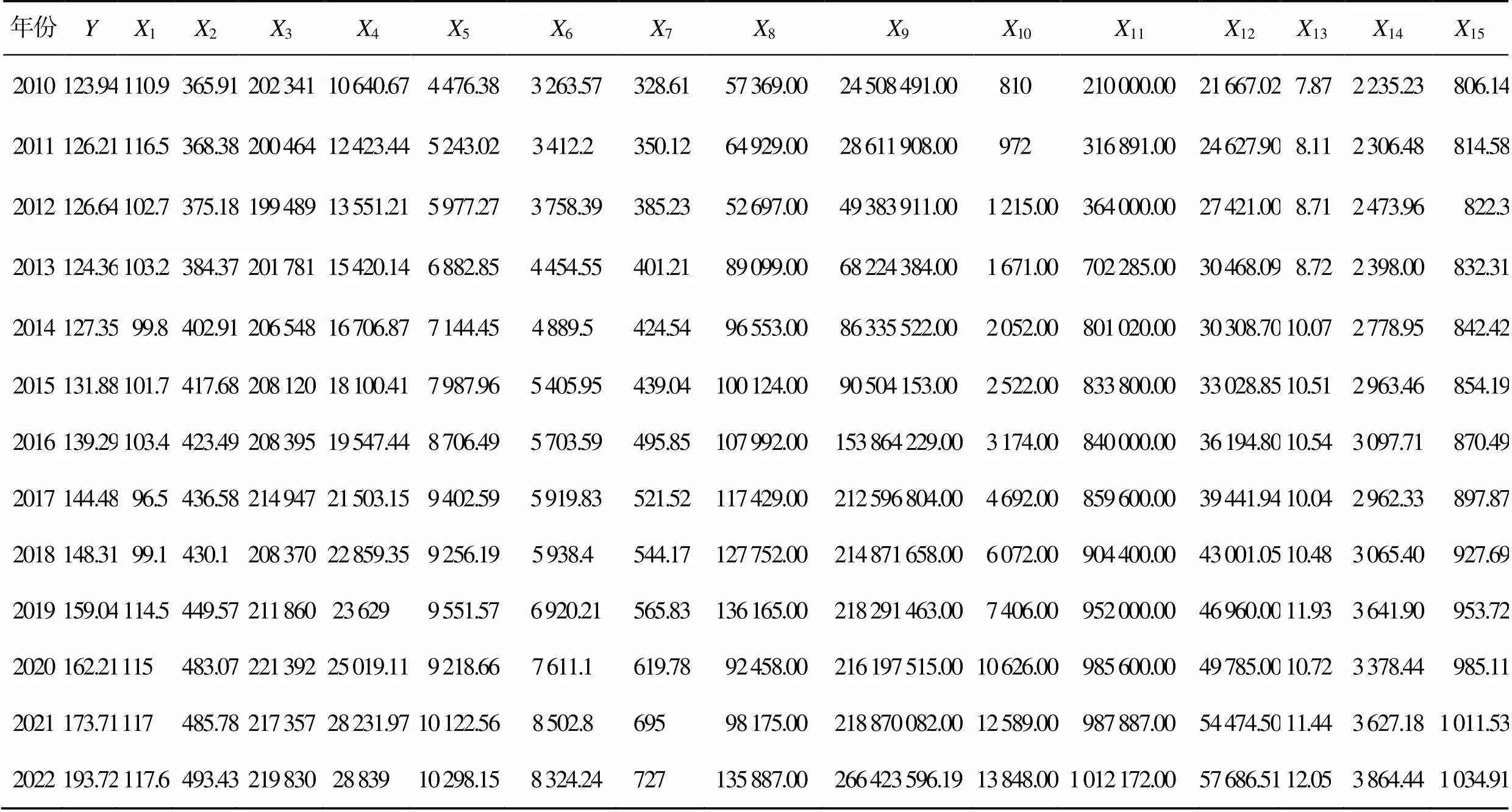
Tab.2 Demand for fresh agricultural products like fruit and vegetable in Guangzhou and data on impact indicators

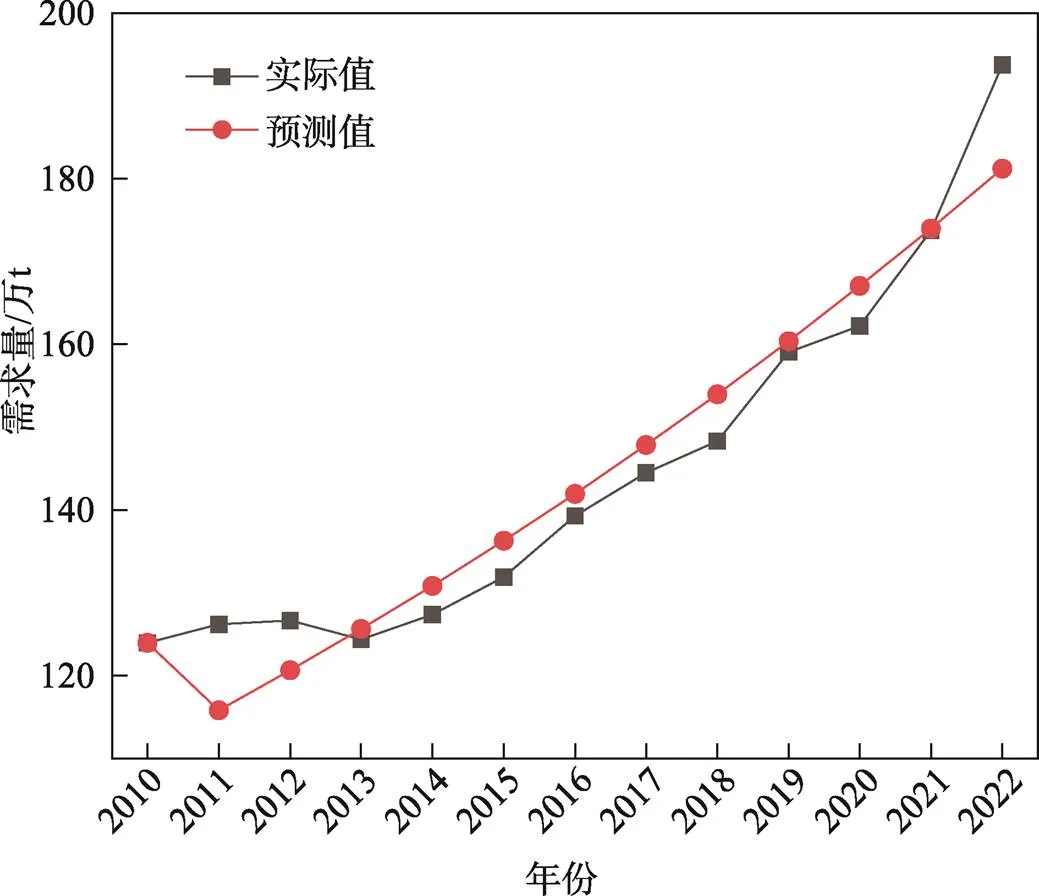
圖1 GM（1，1）模型預測結果

通過計算得出，GM（1，1）模型預測的絕對百分比誤差（MAPE）為2.97%。

3.2.2 GM（1，6）模型分析

3.1節已對本文選取的15個指標進行了灰色關聯度計算，選擇2、15、14、13、7這5個灰色關聯度排名較為靠前的指標，來構建GM（1，6）模型。通過MATLAB軟件進行計算，2010—2022年的預測結果如圖2所示。

通過計算得出，GM（1，6）模型預測的MAPE值為1.70%。

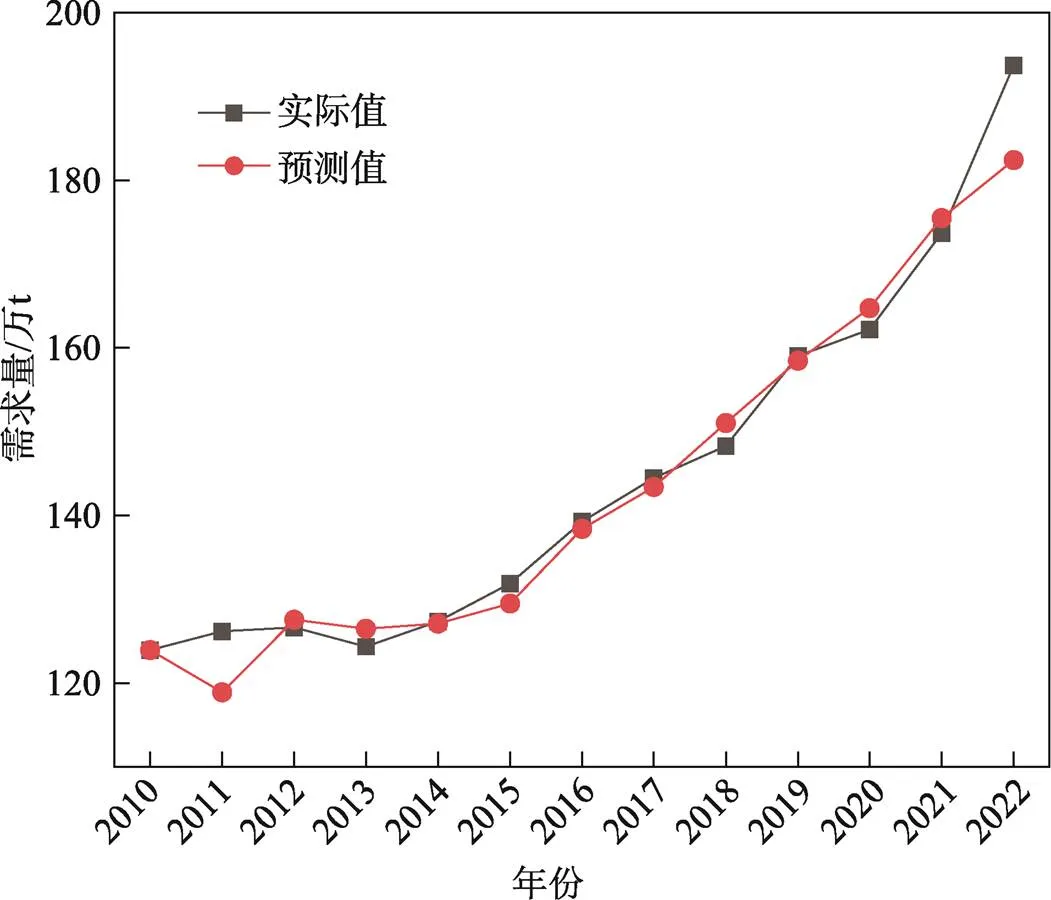
圖2 GM（1，6）模型預測結果

3.2.3 主成分-多元線性回歸模型分析

1）主成分分析。運用SPSS軟件對標準化數據進行主成分分析，各主成分特征值及累積貢獻率見表3。

通過主成分因子分析，可提取出2個特征值大于1的公因子，2個公因子的特征根分別為11.975和1.293，前2個因子的累計方差達到85.537%和94.776%，符合經濟學中成分累計貢獻率大于85%的要求。故將原始的14個指標劃分成2個主成分，通過SPSS軟件得到成分矩陣表，見表4。

表3 總方差解釋

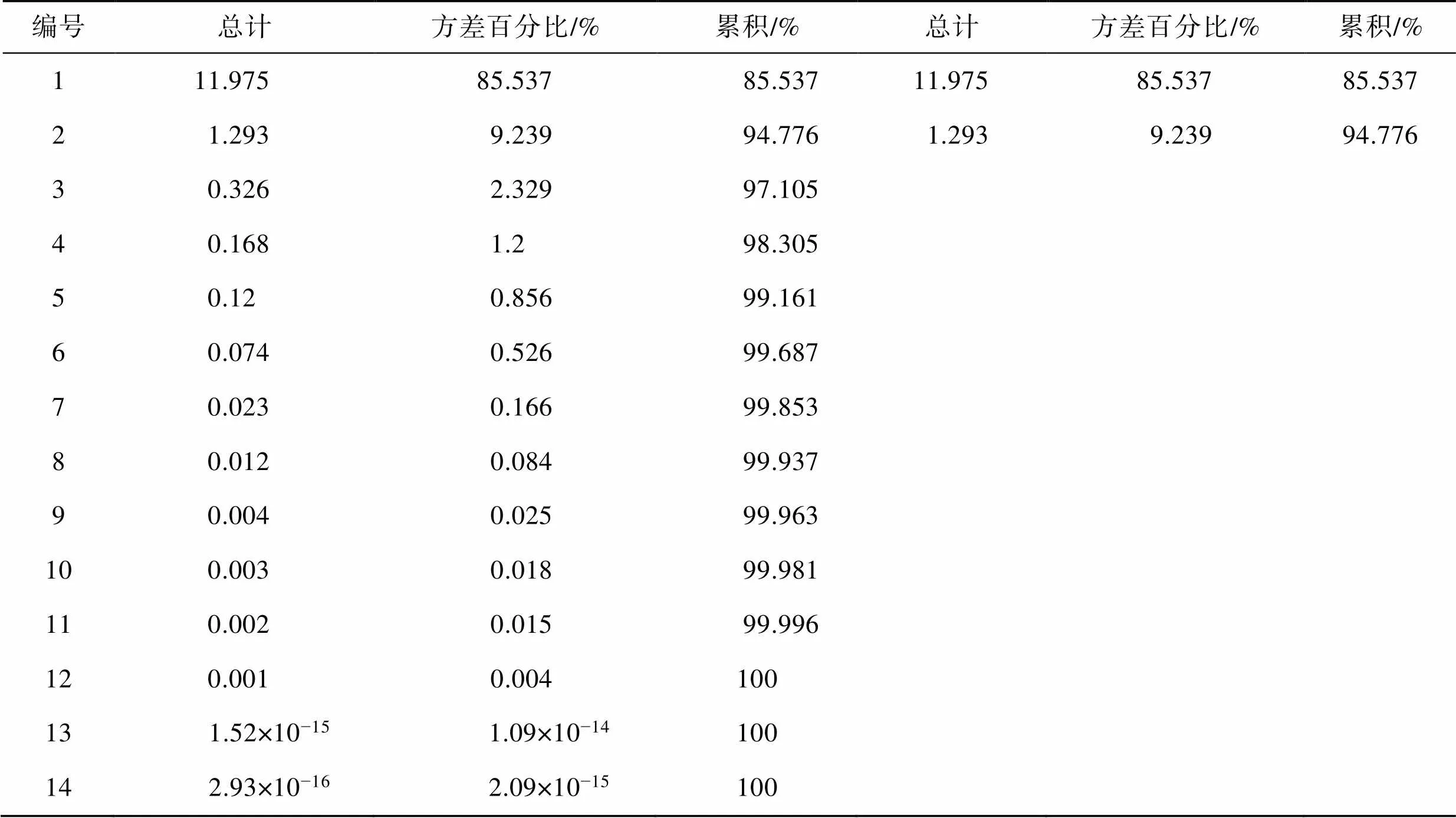
Tab.3 Total variance explanation

表4 成分矩陣

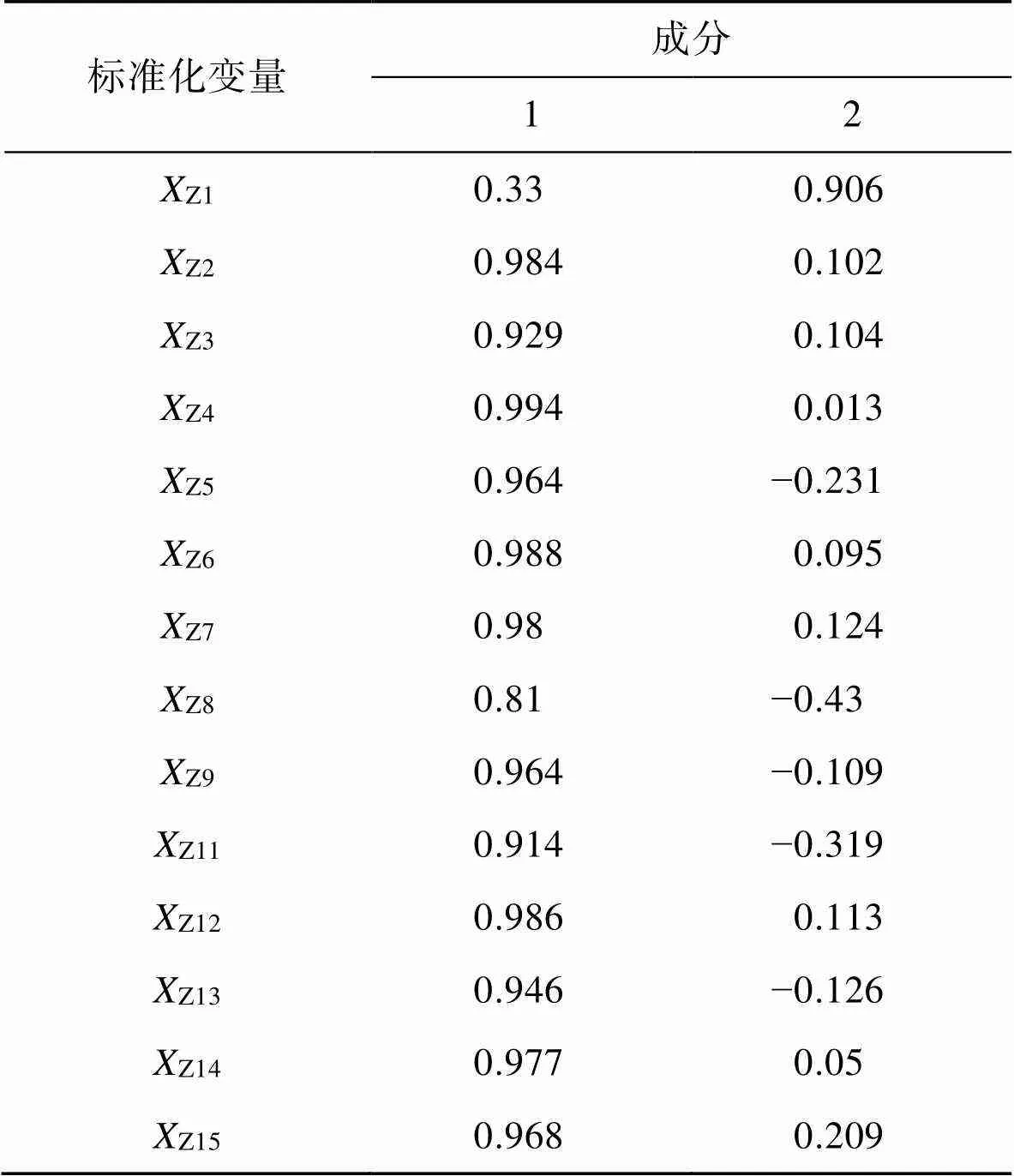
Tab.4 Component matrix

成分矩陣也稱為因子載荷，實質指每個主成分和每個原始變量的相關系數。為了得到主成分分析的系數矩陣，將載荷系數除以對應特征根的平方根，得到主成分表達式如下：

1=0.095Z1+0.284Z2+0.268Z3+0.287Z4+0.279Z5+

0.286Z6+0.283Z7+0.234Z8+0.279Z9+0.264Z11+

0.285Z12+ 0.273Z13+0.282Z14+0.280Z15

2=0.797Z1+0.090Z2+0.091Z3+0.011Z4?0.203Z5+

0.084Z6+0.109Z7?0.378Z8?0.096Z9?0.281Z11+

0.099Z12? 0.111Z13+0.044Z14+0.184Z15

2）多元線性回歸分析。通過SPSS軟件將主成分表達式1和2與進行多元線性回歸分析，得出該模型的2為0.947，回歸模型效果良好。回歸模型系數估計及顯著性檢驗如表5所示。

表5 回歸模型系數及顯著性檢驗

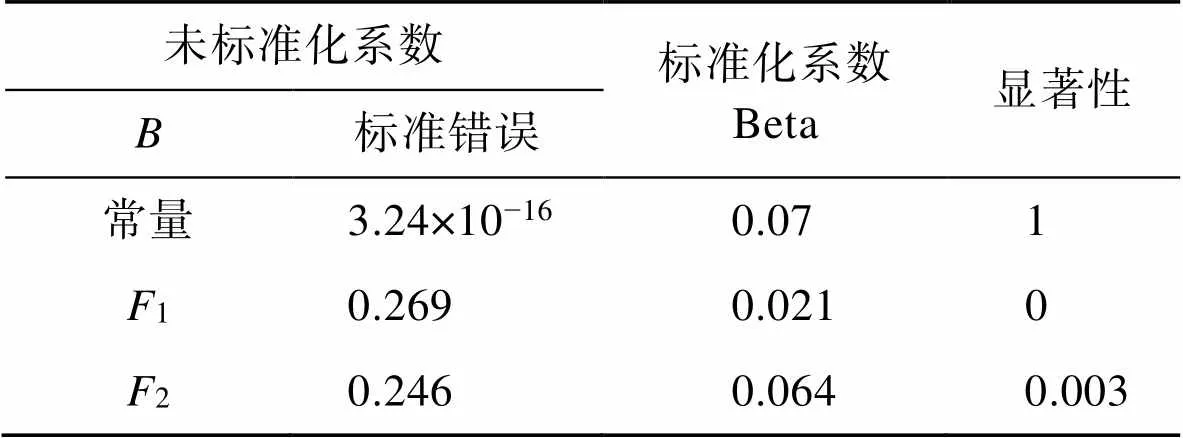
Tab.5 Regression model coefficient and significance test

得到回歸方程：

Z=0.2691+0.2462

將1、2代入上式則得到：

Z=0.222Z1+0.099Z2+0.095Z3+0.080Z4+0.025Z5+

0.097Z6+0.103XZ7?0.030XZ8+0.051XZ9+0.002Z11+

0.101Z12+ 0.046Z13+0.087Z14+1.120Z15

根據標準化公式的逆公式，得出回歸方程：

=0.6221+0.0482+0.000 33+0.000 34+0.000 35+

0.001 26+0.017 77?2×10?58+1.304 2×10?89+

1.627×10?711+0.000 212+0.74013+0.00414+

3.357 2×10?615?80.902

將2010—2022年的原始數據代入得出預測結果，結果見圖3所示。

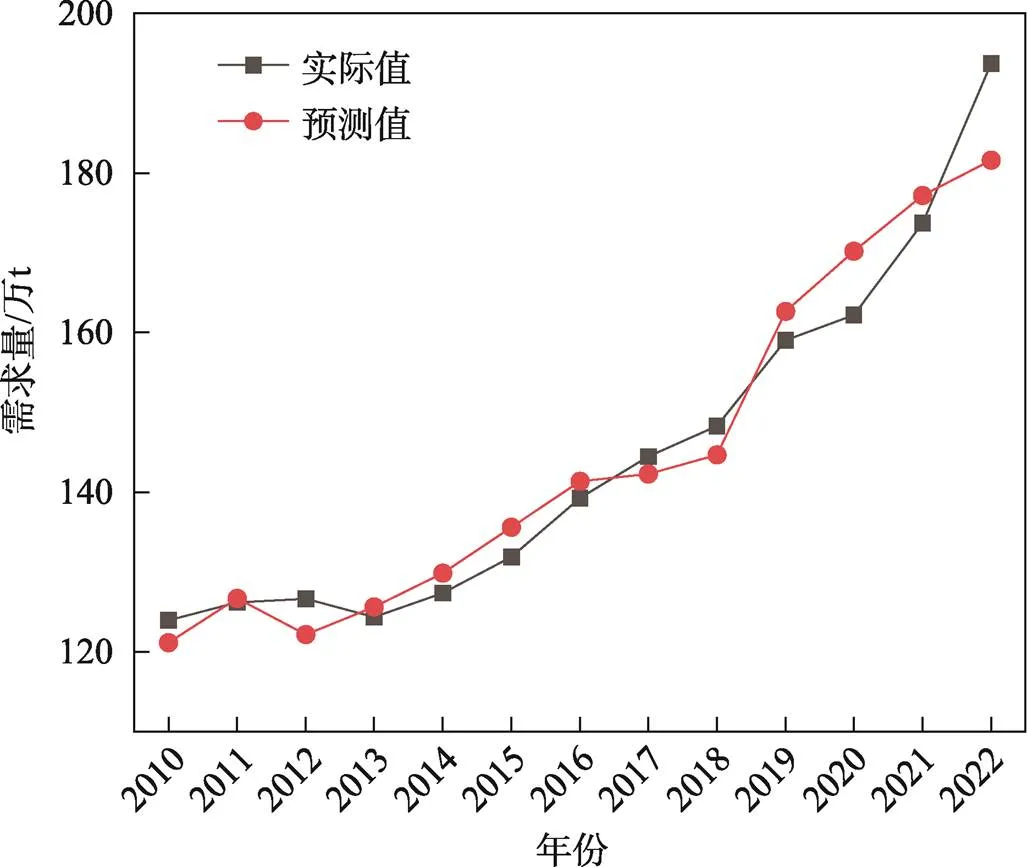
圖3 主成分-多元線性回歸模型預測結果

通過計算得出，主成分-多元線性回歸模型預測的MAPE值為2.53%。對比3種模型，GM（1，6）模型的預測精度最高，除2011年預測誤差較大之外，其余年份預測誤差都較小，由此可見，利用GM（1，6）模型來預測廣州市果蔬類冷鏈物流需求是可行的。

3.2.4 對策建議

1）加強冷鏈基礎設施建設。政府應該增加對現代化冷鏈基礎設施的投資，以保障生鮮產品的品質。據相關數據可知，中國農產品的冷鏈運輸率較低。發達國家的冷鏈運輸率已達到80%～90%的水平，然而，中國果蔬類農產品的冷鏈運輸率只有15%，腐損率卻達到了15%[20]。以1 t蘋果為例：目前廣州市場上蘋果的價格為每公斤13元，如果不采用冷鏈運輸，每1 t蘋果所造成的腐損成本可達到1 950元。盡管冷鏈基礎設施的建設需要較大的資金投入，但考慮到生鮮農產品需求呈持續增長的趨勢，增加冷鏈基礎設施的投資將能夠進一步降低生鮮農產品腐損成本。

2）加快技術升級。采用先進的溫控和追蹤技術，以實時監控冷鏈物流過程的溫度和濕度，確保產品的質量和安全。開發新型的冷鏈包裝材料和技術，以延長冷藏期限，減少產品在儲運過程中的損失。同時，可使用更加節能環保的包裝材料，有助于減少環境負擔，符合可持續發展的原則。

3）制定完備的生鮮物資儲備計劃。在突發事件發生后，居民對生鮮食品物資有著較高需求，完備的儲備計劃可滿足居民在突發事件下對生鮮食品物資的需求。此外，政府開展儲備工作時，應結合物資的特點，采取多種儲備模式，包括政府實物儲備、企業實物儲備和企業合同儲備等，以確保生鮮物資供給的可靠性和持續性。

4 結語

本文以廣州市數據為例，從農產品供給、社會經濟水平、冷鏈物流保障、居民規模與消費能力這四大維度構建了廣州市果蔬類生鮮農產品冷鏈物流需求預測指標體系，通過灰色關聯度對影響指標進行排序，剔除關聯度較低的指標，最終確定指標體系。運用GM（1，1）模型、GM（1，6）模型、主成分-多元線性回歸模型進行預測精度對比。結果表明，GM（1，6）模型的預測精度最高，適用中短期的冷鏈物流需求預測，具有較高的應用價值。

[1] 謝如鶴, 王國利. 冷鏈物流概論[M]. 北京: 中國財富出版社, 2022.

XIE R H, WANG G L. Introduction to Cold Chain Logistics[M]. Beijing: China Fortune Publishing Co., Ltd., 2022.

[2] 廣東省農業農村廳. 2022年年度廣東省蔬菜產銷形勢分析[EB/OL]. (2023-01-30) [2023-11-2]. http://dara. gd.gov.cn/ gkmlpt/content/4/4085/mpost_4085154. html# 3045.

Guangdong Provincial Department of Agriculture and Rural Development. Analysis of Vegetable Production and Marketing Situation in Guangdong Province in 2022[EB/OL]. (2023-01-30) [2023-11-2]. http://dara.gd. gov.cn/gkmlpt/content/4/4085/mpost_4085154. html#3045.

[3] 孟慶龍, 尚靜, 張艷. 蘋果可溶性固形物含量的多元線性回歸預測[J]. 包裝工程, 2020, 41(13): 26-30.

MENG Q L, SHANG J, ZHANG Y. Prediction for Soluble Solids Content of Apples Based on Multi Linear Regression[J]. Packaging Engineering, 2020, 41(13): 26-30.

[4] BESSLER D, WANG Z J. The Homogeneity Restriction and Forecasting Performance of VAR-Type Demand Systems: An Empirical Examination of US Meat Consumption[J]. Journal of Forecasting, 2002, 21(3): 193-206.

[5] 文先明, 肖錦. 基于灰色GM(1, N)模型的湖南省農產品冷鏈物流需求預測[J]. 全國流通經濟, 2021(6): 15-19.

WEN X M, XIAO J. Demand Forecast of Cold Chain Logistics of Agricultural Products in Hunan Province Based on Grey GM(1, N) Model[J]. China Circulation Economy, 2021(6): 15-19.

[6] 周慧, 曾一洲. 數字化轉型背景下九江市生鮮農產品冷鏈物流需求預測及發展建議[J]. 物流科技, 2023, 46(15): 132-137.

ZHOU H, ZENG Y Z. Demand Forecast and Development Suggestion of Cold Chain Logistics of Fresh Agricultural Products in Jiujiang City under the Background of Digital Transformation[J]. Logistics Sci-Tech, 2023, 46(15): 132-137.

[7] EKSOZ C, MANSOURI A, BOURLAKIS M, et al. Judgmental Adjustments through Supply Integration for Strategic Partnerships in Food Chains[J]. Omega, 2018, 87: 20-33.

[8] LIU S, ChANG L, WANG L. Demand Forecasting of Cold-Chain Logistics of Aquatic Products in China under the Background of the Covid-19 Post-Epidemic Era.[J]. PloS one, United States: 2023, 18(11): 0287030.

[9] MA H J, LUO X. Logistics Demand Forecasting Model Based on Improved Neural Network Algorithm[J]. Journal of Intelligent & Fuzzy Systems, 2020, 40(1): 1-11.

[10] REN X Y, TAN J, QIAO Q M, et al. Demand Forecast and Influential Factors of Cold Chain Logistics Based on a Grey Model[J]. Mathematical Biosciences and Engineering, 2022, 19(8): 7669-7686.

[11] 徐曉燕, 楊慧敏, 呂修凱, 等. 基于山東省不同模型的物流需求預測比較研究[J]. 包裝工程, 2022, 43(23): 207-215.

XU X Y, YANG H M, LYU X K, et al. Comparative Research on Forecast of Logistics Demand in Shandong Province Based on Different Models[J]. Packaging Engineering, 2022, 43(23): 207-215.

[12] 劉艷利, 伍大清. 基于改進BP神經網絡的水產品冷鏈物流需求預測研究——以浙江省為例[J]. 中國漁業經濟, 2020, 38(5): 93-101.

LIU Y L, WU D Q. Research on Cold Chain Logistics Demand Prediction of Aquatic Products Based on Improved BP Neural Network: a Case Study of Zhejiang Province[J]. China Fisheries Economy, 2020, 38(5): 93-101.

[13] HUANG L J, XIE G J, ZHAO W D, et al. Regional Logistics Demand Forecasting: A BP Neural Network Approach[J]. Complex & Intelligent Systems, 2023, 9(3): 2297-2312.

[14] YANG D N. Logistics Demand Forecast Model for Port Import and Export in Coastal Area[J]. Journal of Coastal Research, 2020, 103: 678.

[15] HE B, YIN L J. Prediction Modelling of Cold Chain Logistics Demand Based on Data Mining Algorithm[J]. Mathematical Problems in Engineering, 2021(5): 1-9.

[16] 李小玲. 基于GM(1,)模型的廣東省生鮮農產品冷鏈物流需求預測研究[J]. 物流科技, 2022, 45(7): 143-147.

LI X L. Research on Cold Chain Logistics Demand Prediction of Fresh Agricultural Products in Guangdong Province Based on GM (1,) Model[J]. logistics technology, 2022, 45(7): 143-147.

[17] 王曉平, 閆飛. 基于GA-BP模型的北京城鎮農產品冷鏈物流需求預測[J]. 數學的實踐與認識, 2019, 49(21): 17-27.

WANG X P, YAN F. Prediction of Cold Chain Logistics Demand for Agricultural Products in Beijing Based on GA-BP Model[J]. Journal of Mathematics in Practice and Theory, 2019, 49(21): 17-27.

[18] 李思聰, 葉靜. 基于灰色回歸模型的農產品冷鏈物流需求分析及預測[J]. 公路交通科技, 2022, 39(5): 166-174.

LI S C, YE J. Analysis and Forecast on Cold Chain Logistics Demand of Agricultural Products Based on Grey Regression Model[J]. Journal of Highway and Transportation Research and Development, 2022, 39(5): 166-174.

[19] 詹昕, 姚奔, 金誠, 等. 基于K-means和主成分回歸的電網線損率影響因素分析[J]. 計算機應用研究, 2020, 37(S2): 108-109.

ZHAN X, YAO B, JIN C, et al. Analysis of Factors Affecting Power Grid Line Loss Rate Based on K-Means and Principal Component Regression[J]. Computer Applications Research, 2020, 37(S2): 108-109.

[20] 中華人民共和國國家發展和改革委員會. 我國冷鏈物流發展的現狀、困境與政策建議[EB/OL]. (2021-06-11)[2023-09-11]. https://www.ndrc.gov.cn/xxgk/ jd/wsdwhfz/202106/t20210611_1283162.html.

National Development and Reform Commission of the People's Republic of China. Status Quo, Dilemmas and Policy Recommendations for the Development of Cold Chain Logistics in China[EB/OL]. (2021-06-11)[2023-09-11]. https://www.ndrc.gov.cn/xxgk/jd/wsdwhfz/202106/t20210611_1283162. html.

Cold Chain Logistics Demand Forecast for Fresh Agricultural Products like Fruit and Vegetable in Guangzhou City Based on Gray Regression Model

LIU Ziling1, XIE Ruhe1*, LIAO Jing2, HE Jiawen1, LUO Huqiao3

(1. Guangzhou University, Guangzhou 510006, China; 2. Guangzhou Panyu Polytechnic, Guangzhou 511483, China; 3. Guangdong Asia-Pacific Economic Index Research Center, Guangzhou 510040, China)

The work aims to conduct a comparative study on the errors of different forecast methods, so as to select the method with higher accuracy and promote the scientific decision-making of relevant departments. Fifteen indicators were selected from the four dimensions of agricultural supply, socio-economic level, cold chain logistics security, size of the population and consumption capacity to construct the indicator system of influencing factors, and a gray correlation analysis was carried out between each influencing factor and cold chain logistics demand. The GM(1, 1) prediction model, GM(1, 6) prediction model and principal component-multiple regression linear prediction model were used to forecast cold chain logistics demand. The prediction errors of the GM(1, 1) prediction model, GM(1, 6) prediction model and principal component-multiple regression linear prediction model were 2.97%, 1.70% and 2.53%. The GM(1, 6) prediction model has high prediction accuracy, which is suitable for short and medium term cold chain logistics demand forecast and has high application value.

fresh agricultural products like fruit and vegetable; gray prediction model; principal component-multiple regression linear; demand forecast

TB485.3；F252.21

A

1001-3563(2024)03-0243-08

10.19554/j.cnki.1001-3563.2024.03.028

2023-09-18

國家社會科學基金項目（17BJY102）；廣東省農產品保鮮物流共性關鍵技術研發創新團隊（2021KJ145）