改進(jìn)麻雀搜索算法求解多目標(biāo)低碳冷鏈物流車(chē)輛路徑問(wèn)題

楊超，張惠珍，錢(qián)隴駿

改進(jìn)麻雀搜索算法求解多目標(biāo)低碳冷鏈物流車(chē)輛路徑問(wèn)題

楊超，張惠珍*，錢(qián)隴駿

（上海理工大學(xué) 管理學(xué)院，上海 200093）

在傳統(tǒng)冷鏈物流的車(chē)輛路徑問(wèn)題模型基礎(chǔ)上，考慮服務(wù)節(jié)點(diǎn)和車(chē)輛運(yùn)輸過(guò)程中產(chǎn)生的碳排放，并加入客戶(hù)滿(mǎn)意度，在有限資源情況下最小化路徑成本和最大化客戶(hù)滿(mǎn)意度。構(gòu)建多目標(biāo)低碳冷鏈物流車(chē)輛路徑問(wèn)題模型，將爬山算法局部搜索思想應(yīng)用到麻雀搜索算法中，形成改進(jìn)麻雀搜索算法，并用其對(duì)上海市某區(qū)域內(nèi)的冷鏈物流配送路徑優(yōu)化問(wèn)題算例進(jìn)行求解。通過(guò)與改進(jìn)前及其他2種智能優(yōu)化算法運(yùn)行結(jié)果進(jìn)行對(duì)比發(fā)現(xiàn)，改進(jìn)后的麻雀搜索算法具有更快的尋優(yōu)速度和更好的尋優(yōu)能力，且改進(jìn)后的算法對(duì)模型的碳排放效用性更高。基于國(guó)家的低碳政策，設(shè)計(jì)出符合當(dāng)下實(shí)情的低碳冷鏈物流運(yùn)輸模型，通過(guò)改進(jìn)優(yōu)化算法設(shè)計(jì)運(yùn)輸方案，驗(yàn)證了爬山算法局部搜索思想對(duì)麻雀搜索算法進(jìn)行改進(jìn)的有效性及所構(gòu)建低碳冷鏈物流車(chē)輛路徑模型的合理性。

車(chē)輛路徑問(wèn)題；多目標(biāo)；低碳；爬山算法；局部搜索；麻雀搜索算法

車(chē)輛路徑問(wèn)題（Vehicle routing problem，VRP）是近年來(lái)物流運(yùn)籌規(guī)劃和智能優(yōu)化算法應(yīng)用研究的重要內(nèi)容之一。通過(guò)優(yōu)化運(yùn)輸路徑可使整個(gè)物流供應(yīng)鏈得到改善[1]，整個(gè)供應(yīng)鏈的效率更高、成本更低，同時(shí)還能提升顧客滿(mǎn)意度。

隨著各種工業(yè)技術(shù)的發(fā)展成熟，冷鏈物流運(yùn)輸網(wǎng)絡(luò)越來(lái)越完善。伴隨著冷鏈物流的發(fā)展，環(huán)境問(wèn)題成為目前發(fā)展道路上需要考慮解決的重要問(wèn)題。Kuo等[2]在對(duì)冷鏈物流配送模式研究的基礎(chǔ)上，根據(jù)不同產(chǎn)品具有不同的配送溫度，提出并構(gòu)建了多溫度冷鏈物流配送路徑優(yōu)化模型，提高了整個(gè)冷鏈配送網(wǎng)絡(luò)的響應(yīng)度。不同的車(chē)輛有著不同的配送方式，存在不同的配送成本和風(fēng)險(xiǎn)。丁艷[3]采用歸一化法對(duì)多目標(biāo)成本進(jìn)行了統(tǒng)一計(jì)算，使得優(yōu)化結(jié)果更加合理。李四蘭等[4]在模型構(gòu)建中考慮了碳排放問(wèn)題，將碳排放以碳稅成本體現(xiàn)在模型中。王淑云等[5]根據(jù)客戶(hù)需求構(gòu)建了隨機(jī)需求下的多溫共配模型，使得模型更加合理。

由于VRP屬于NP-hard問(wèn)題[6]，所以在面對(duì)大規(guī)模的此類(lèi)問(wèn)題時(shí)，無(wú)法使用精確算法對(duì)其在規(guī)定的多項(xiàng)式時(shí)間內(nèi)進(jìn)行求解。針對(duì)VRP求解，目前常用的優(yōu)化算法有遺傳算法[7]、模擬退火算法[8]和禁忌搜索算法[9]等。遺傳算法能夠較好地避免陷入局部最優(yōu)，可以適應(yīng)多樣化問(wèn)題，但其計(jì)算復(fù)雜度較高，且對(duì)問(wèn)題的編碼和參數(shù)設(shè)置較敏感。模擬退火算法能夠在一定程度上跳出局部最優(yōu)解，在搜索過(guò)程中可根據(jù)問(wèn)題的特點(diǎn)靈活地定義初始解和鄰域搜索操作，但對(duì)于復(fù)雜問(wèn)題需要合理的參數(shù)調(diào)節(jié)和退火策略。禁忌搜索算法具有較強(qiáng)的全局搜索能力，能夠適應(yīng)不同的問(wèn)題約束和目標(biāo)函數(shù)，通過(guò)調(diào)整禁忌表和禁忌規(guī)則的設(shè)置，靈活地求解問(wèn)題，但在處理大規(guī)模問(wèn)題時(shí)對(duì)計(jì)算成本和問(wèn)題參數(shù)調(diào)節(jié)的要求較高。

麻雀搜索算法（Sparrow Search Algorithm，SSA）[10]是2020年提出的新型智能優(yōu)化算法，針對(duì)每個(gè)優(yōu)化問(wèn)題的解類(lèi)似于搜索空間中的一只麻雀，每只麻雀都具有各自的能量，采用函數(shù)適應(yīng)度來(lái)表示能量。其中，將麻雀分為發(fā)現(xiàn)者和參與者，發(fā)現(xiàn)者的適應(yīng)度通常大于參與者的適應(yīng)度。SSA具有收斂速度快、參數(shù)較少且算法易實(shí)現(xiàn)等優(yōu)點(diǎn)。為了提高麻雀種群的群體多樣性，在領(lǐng)頭鳥(niǎo)初始化過(guò)程中，文獻(xiàn)[11]通過(guò)SSA和0-1規(guī)劃提出了一般生鮮倉(cāng)庫(kù)選址問(wèn)題的解決方案。阮信波等[12]通過(guò)對(duì)比SSA和粒子群算法（Particle swarm optimization，PSO），提出了SSA的缺點(diǎn)和改進(jìn)方向。馮增喜等[13]根據(jù)精英反向?qū)W習(xí)策略對(duì)SSA的運(yùn)行結(jié)果進(jìn)行了反向?qū)Ρ仍u(píng)估，確保算法的結(jié)果更優(yōu)。蘇瑩瑩、王升旭[14]針對(duì)SSA初始種群質(zhì)量問(wèn)題提出了混沌映射初始化精英種群策略，提高了初始解質(zhì)量，從而提升了算法的效率。陳登旭等[15]對(duì)比了爬山算法（Hill Climbing）和PSO，并分析了2種算法的計(jì)算收斂效率。

目前，SSA極少用于路徑優(yōu)化。Ouyang等[16]提出，SSA高度依賴(lài)種群中的最優(yōu)個(gè)體，缺乏學(xué)習(xí)能力，在求解高維復(fù)雜的優(yōu)化問(wèn)題時(shí)容易陷入局部最優(yōu)。將爬山算法對(duì)個(gè)體最優(yōu)的局部搜索思想應(yīng)用于SSA中，形成了改進(jìn)麻雀搜索算法（Improved Sparrow Search Algorithm，ISSA）。采用ISSA求解含滿(mǎn)意度的低碳冷鏈物流VRP模型案例，通過(guò)與改進(jìn)前算法運(yùn)算結(jié)果進(jìn)行對(duì)比發(fā)現(xiàn)，改進(jìn)后的算法具有更快的尋優(yōu)速度和更好的尋優(yōu)能力，通過(guò)與其他2種優(yōu)化算法的結(jié)果進(jìn)行對(duì)比發(fā)現(xiàn)該算法具有較好的有效性和模型合理性。

1 問(wèn)題描述及模型構(gòu)建

在經(jīng)典VRP模型的基礎(chǔ)上結(jié)合冷鏈物流獨(dú)有的特點(diǎn)，并考慮以下幾方面：運(yùn)輸過(guò)程中汽車(chē)燃油所產(chǎn)生的碳排放及車(chē)輛在各需求點(diǎn)裝卸貨物時(shí)產(chǎn)生的節(jié)點(diǎn)碳排放；由于需要保證冷鏈生鮮食品的新鮮度，所以存在運(yùn)輸過(guò)程中因食品新鮮程度發(fā)生變化而造成的貨損成本；根據(jù)是否在客戶(hù)期望時(shí)間內(nèi)送達(dá)而產(chǎn)生的早到或遲到懲罰成本[17]；客戶(hù)根據(jù)產(chǎn)品送達(dá)時(shí)間產(chǎn)生的滿(mǎn)意度[18]。已知每個(gè)客戶(hù)點(diǎn)的需求量和地理坐標(biāo)，已知車(chē)輛的最大載重量及滿(mǎn)載空載時(shí)的單位距離耗油量。以最小化成本和最大化客戶(hù)滿(mǎn)意度為目標(biāo)進(jìn)行優(yōu)化，計(jì)算出最優(yōu)的運(yùn)輸方案。在構(gòu)建模型時(shí)做如下假設(shè)。

1）所有客戶(hù)均由一個(gè)配送中心配送。

2） 所有車(chē)輛都為同一類(lèi)型，在同等環(huán)境下單位距離燃油量及載重能力相同。

3） 所有客戶(hù)點(diǎn)的需求均能被滿(mǎn)足，且每個(gè)客戶(hù)點(diǎn)只由1輛車(chē)服務(wù)。

4） 所有車(chē)輛在完成配送任務(wù)后必須返回配送中心，中途不考慮車(chē)輛損壞等特殊情況。

5） 車(chē)輛必須在客戶(hù)可接受時(shí)間內(nèi)服務(wù)。

6） 客戶(hù)點(diǎn)的需求量、可接受服務(wù)時(shí)間及車(chē)輛在該點(diǎn)需要提供服務(wù)的時(shí)長(zhǎng)均已知。

7） 所運(yùn)輸產(chǎn)品均為冷凍生鮮食品。

8） 配送路線上所有客戶(hù)需求量之和不能超過(guò)該路線運(yùn)輸車(chē)輛最大載重。

9） 裝卸過(guò)程的碳排放量與車(chē)輛冷庫(kù)實(shí)時(shí)溫度無(wú)關(guān)，只與開(kāi)倉(cāng)時(shí)間有關(guān)。

10）客戶(hù)滿(mǎn)意度計(jì)算原理：在顧客期望的時(shí)間內(nèi)送達(dá)，則客戶(hù)滿(mǎn)意度達(dá)到最高值，定義為1；在客戶(hù)其他可接受的時(shí)間內(nèi)送達(dá)，則根據(jù)距離期望時(shí)間段的長(zhǎng)短來(lái)判定客戶(hù)的滿(mǎn)意度。滿(mǎn)意度與時(shí)間呈線性關(guān)系[19]，如果在客戶(hù)可接受時(shí)間外送達(dá)，則客戶(hù)滿(mǎn)意度為0，如圖1所示。

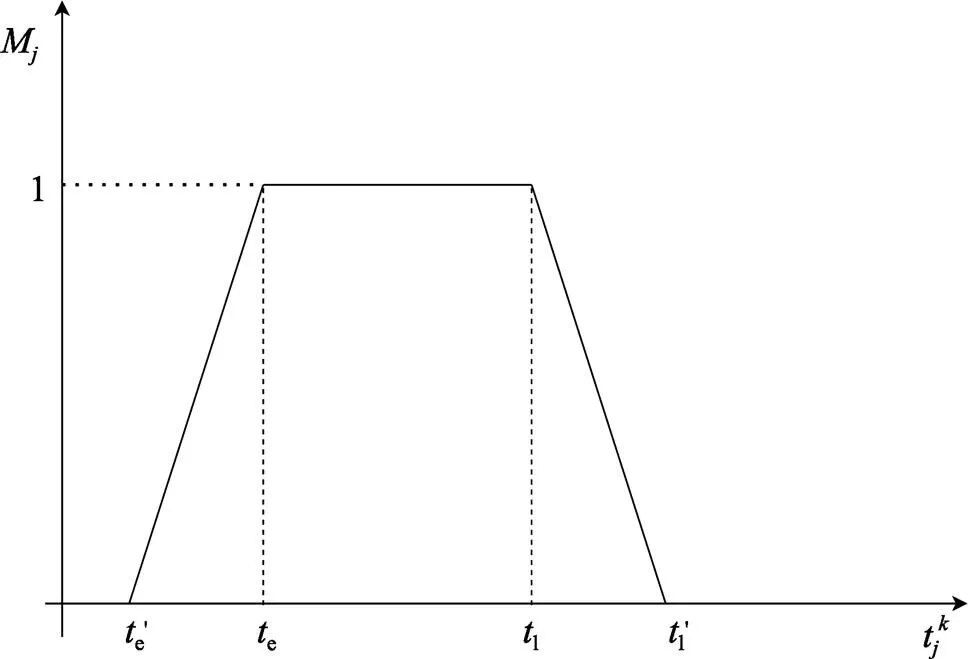
圖1 送達(dá)時(shí)間與客戶(hù)滿(mǎn)意度關(guān)系

模型參數(shù)說(shuō)明：表示配送中心和所有小區(qū)的集合，{0, 1, 2, … ,}，∈；表示車(chē)輛集合，∈；z表示車(chē)輛在需求點(diǎn)的裝卸時(shí)間；t表示從到的運(yùn)輸時(shí)間；d表示從到的歐氏距離；表示車(chē)輛到需求點(diǎn)卸貨時(shí)的單位時(shí)間碳排放量；Q表示小區(qū)的需求量；h表示車(chē)輛的啟動(dòng)成本；c表示車(chē)輛的單位距離運(yùn)輸成本；z表示裝卸貨物時(shí)單位碳排放價(jià)格；t表示車(chē)輛運(yùn)輸途中單位碳排放價(jià)格；s表示冷凍生鮮食品的單位售價(jià)；表示冷凍生鮮食品的腐敗率；表示碳排放率；max表示車(chē)輛的最大載重量；1表示車(chē)輛滿(mǎn)載時(shí)的單位距離油耗；0表示車(chē)輛空車(chē)時(shí)的單位距離油耗；H表示車(chē)輛在路徑上的單位距離油耗；Q表示車(chē)輛在到這條路徑上的實(shí)際載重量；t表示車(chē)輛到達(dá)點(diǎn)的時(shí)間；e表示車(chē)輛早到時(shí)單位時(shí)間的懲罰成本；l表示車(chē)輛晚到時(shí)單位時(shí)間的懲罰成本；[e,l]表示客戶(hù)期望的配送到達(dá)時(shí)間；[e',l']表示客戶(hù)可接受的配送到達(dá)時(shí)間；(t)表示車(chē)輛遲到或早到的懲罰函數(shù)；M表示客戶(hù)滿(mǎn)意度函數(shù)；表示車(chē)輛的行駛速度；x表示如果第輛車(chē)從小區(qū)到小區(qū)則為1，否則為0；z表示如果車(chē)輛到達(dá)點(diǎn)時(shí)發(fā)生貨損則為1，否則為0。

在以上模型假設(shè)的基礎(chǔ)上構(gòu)建低碳冷鏈物流VRP模型，見(jiàn)式（1）～（13）。

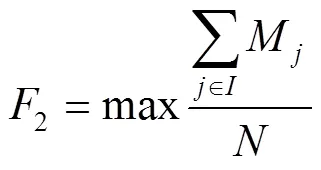
s. t.

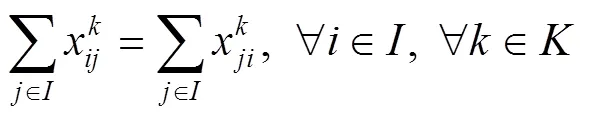
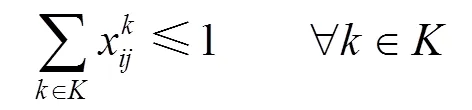
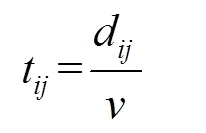
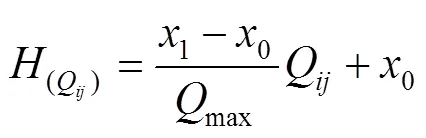
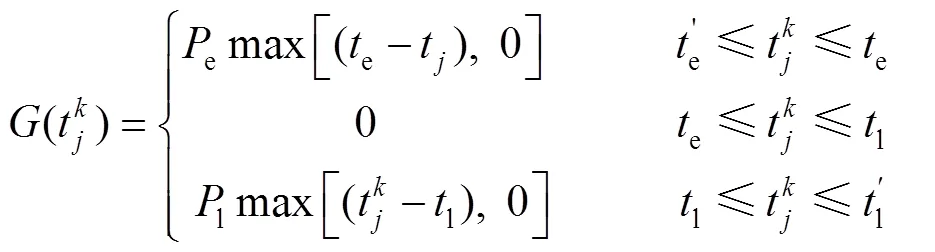
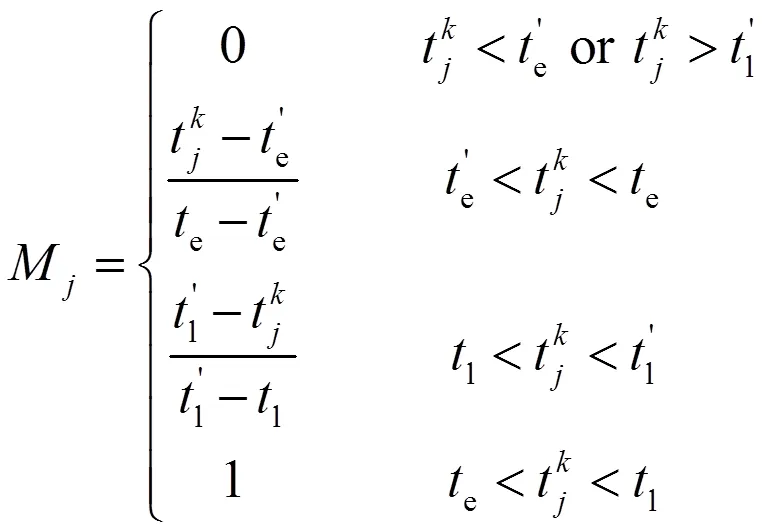
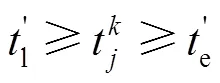
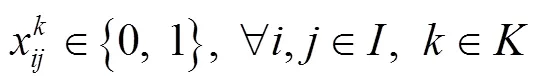
式（1）為最小化成本函數(shù)，其中，第1項(xiàng)為車(chē)輛使用成本，第2項(xiàng)為車(chē)輛運(yùn)輸成本，第3項(xiàng)為車(chē)輛在運(yùn)輸途中的碳排放成本，第4項(xiàng)為車(chē)輛在需求節(jié)點(diǎn)的碳排放成本，第5項(xiàng)為運(yùn)輸途中發(fā)生的貨損成本，第6項(xiàng)為車(chē)輛早到或遲到的懲罰成本。式（2）為最大化滿(mǎn)意度函數(shù)。式（3）表示每個(gè)需求點(diǎn)有且只有1輛車(chē)服務(wù)，式（4）表示車(chē)輛駛?cè)肽承枨簏c(diǎn)后必須駛出。式（5）表示一條路徑的總需求量不得超過(guò)車(chē)輛的最大載重量。式（6）表示每輛車(chē)的行駛路徑最多只有1條。式（7）表示行駛時(shí)間。式（8）表示車(chē)輛行駛單位距離的油耗。式（9）為車(chē)輛早到或遲到的懲罰函數(shù)。式（10）為客戶(hù)滿(mǎn)意度的計(jì)算函數(shù)。式（11）表示運(yùn)輸?shù)竭_(dá)需求點(diǎn)的時(shí)間必須在客戶(hù)可接受時(shí)間范圍內(nèi)。式（12）、（13）為決策變量約束。

2 算法描述

2.1 爬山算法局部搜索

爬山算法是一種簡(jiǎn)單的貪心搜索算法，該算法每次從當(dāng)前解的臨近解空間中選擇一個(gè)最優(yōu)解作為當(dāng)前解，通過(guò)算法迭代，直到尋出一個(gè)最優(yōu)解。具體步驟：將當(dāng)前解初始化為隨機(jī)解或預(yù)定義解；計(jì)算當(dāng)前解的評(píng)估值（目標(biāo)函數(shù)值）；在當(dāng)前解的鄰域內(nèi)搜索更優(yōu)的解；如果找到了更優(yōu)的解，則將當(dāng)前解更新為該解，并更新評(píng)估值；重復(fù)前2個(gè)步驟，直到達(dá)到一個(gè)無(wú)法改進(jìn)的局部最優(yōu)解，或滿(mǎn)足迭代停止條件。

2.2 改進(jìn)麻雀搜索算法

傳統(tǒng)的SSA針對(duì)單目標(biāo)連續(xù)優(yōu)化問(wèn)題的求解具有良好的收斂效果，但在針對(duì)多目標(biāo)離散優(yōu)化問(wèn)題時(shí)，算法在運(yùn)行時(shí)容易陷入局部最優(yōu)，且不能快速有效地選擇目標(biāo)全局最優(yōu)和個(gè)體最優(yōu)。針對(duì)個(gè)體最優(yōu)的選擇，使用爬山算法局部搜索思想對(duì)SSA進(jìn)行改進(jìn)。

在最優(yōu)非劣解集中，利用網(wǎng)格法[20]（在2.3.4節(jié)中詳解）選取最優(yōu)個(gè)體，然后利用爬山算法多目標(biāo)局部搜索的優(yōu)化思想[21]，對(duì)個(gè)體最優(yōu)進(jìn)行局部搜索操作。具體步驟：獲取最優(yōu)層級(jí)的個(gè)體0后，計(jì)算個(gè)體的適應(yīng)度；在0中以一定的概率選擇一個(gè)位置進(jìn)行變異操作，得到新個(gè)體0，并計(jì)算適應(yīng)度；比較0和0的支配關(guān)系，如果0支配0，則更新最優(yōu)個(gè)體1=0，如果0支配0，則更新最優(yōu)個(gè)體1=0，否則以0.5的概率接受1=0；對(duì)層級(jí)個(gè)體重新進(jìn)行非支配排序，并輸出結(jié)果。

麻雀搜索算法的最優(yōu)個(gè)體經(jīng)過(guò)爬山算法鄰域搜索重新選擇后，能夠保證每次迭代都得到不劣于算法改進(jìn)前的最優(yōu)個(gè)體，在一定程度上避免陷入局部最優(yōu)。

2.3 算法流程

2.3.1 編碼與解碼

由于麻雀搜索算法為連續(xù)型優(yōu)化算法[22]，而VRP所求問(wèn)題為離散型優(yōu)化，所以采用的編碼方式為排序的連續(xù)型編碼，原理如圖2所示。將每個(gè)個(gè)體進(jìn)行連續(xù)編碼后，再將其按照從小到大的順序進(jìn)行排序，并記錄編號(hào)，轉(zhuǎn)為自然數(shù)編碼，編碼長(zhǎng)度為該路徑上需要配送的客戶(hù)點(diǎn)數(shù)量。定義0為配送中心，對(duì)染色體解碼，圖2中第1輛車(chē)的配送路徑為{0，2，6，7，8，1，0}，第2輛車(chē)的配送路徑為{0，10，3，4，9，5，0}，路徑配送方案的生成均以客戶(hù)可接受到達(dá)時(shí)間和車(chē)輛最大載重為約束。最后得到該方案的完整配送路線為{0，2，6，7，8，1，0，10，3，4，9，5，0}。

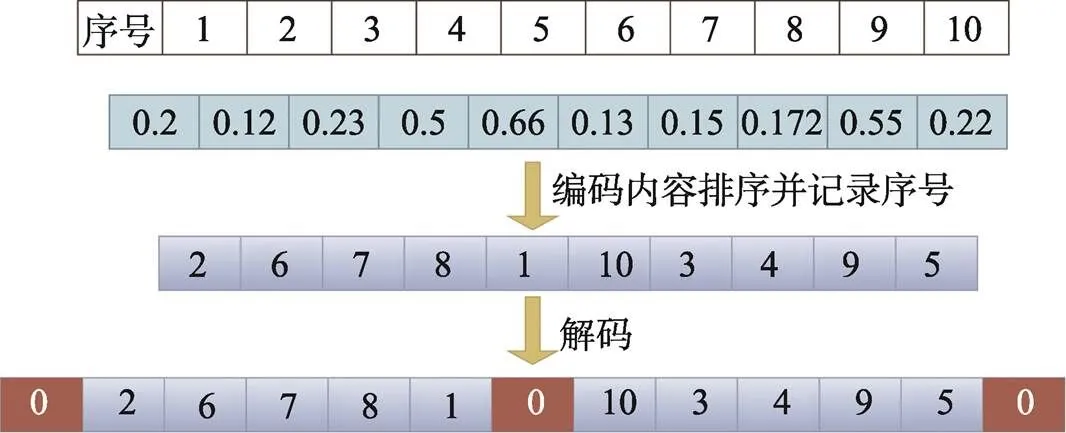
圖2 編碼與解碼

2.3.2 初始化種群

初始化麻雀種群的計(jì)算見(jiàn)式（14）。其中，為所求優(yōu)化問(wèn)題的客戶(hù)數(shù)量，為麻雀種群數(shù)量。矩陣的每行均由2.3.1節(jié)編碼方式生成。

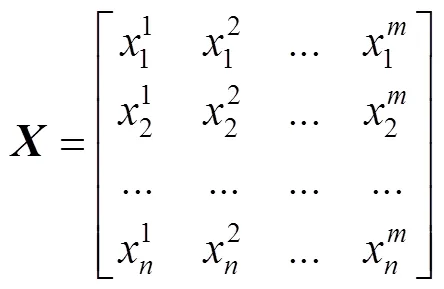
2.3.3 生成非劣解集

解碼并計(jì)算目標(biāo)函數(shù)值，包括配送路徑的總成本和滿(mǎn)意度。對(duì)解集進(jìn)行非支配排序，將非劣解拷貝到Archive集中，記為A，并外部存檔，形成pareto解集。

2.3.4 選取最優(yōu)個(gè)體

用網(wǎng)格法計(jì)算次迭代A中麻雀的密度信息：將目標(biāo)空間采用式（15）劃分成大小相等的區(qū)域，將每個(gè)區(qū)域內(nèi)包含的麻雀數(shù)量作為麻雀的密度信息。在網(wǎng)格中，麻雀的數(shù)量越多，則密度越大。實(shí)現(xiàn)過(guò)程如下。

1）計(jì)算次迭代的目標(biāo)函數(shù)邊界（min1，max1）和（min2，max2）。

2）計(jì)算網(wǎng)格的規(guī)模，見(jiàn)式（15）。

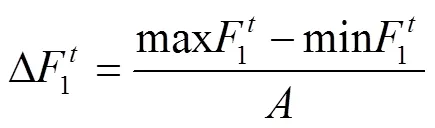
3）遍歷A中的麻雀?jìng)€(gè)體，用式（16）計(jì)算它在網(wǎng)格中的編號(hào)。

式中：為需要?jiǎng)澐值木W(wǎng)格數(shù)量；Int()為取整函數(shù)；1、2為目標(biāo)函數(shù)值。

4）記錄編號(hào)，并統(tǒng)計(jì)A中麻雀密度信息估計(jì)值。將Archive中的麻雀?jìng)€(gè)體目標(biāo)值的計(jì)算結(jié)果與初始麻雀種群目標(biāo)值進(jìn)行對(duì)比，優(yōu)于初始群體中的麻雀數(shù)量越多，說(shuō)明其搜索能力越強(qiáng)，反之則越弱。解集A用于存放A中優(yōu)秀的麻雀?jìng)€(gè)體，密度越低，被選擇的概率越大。A∈A，計(jì)算個(gè)體A的密度估計(jì)值，將最小密度的個(gè)體存于G中，g=rand{G}表示在G中隨機(jī)選擇一個(gè)最優(yōu)個(gè)體g。對(duì)于更新過(guò)的最優(yōu)個(gè)體利用2.2節(jié)中的改進(jìn)算法進(jìn)行局部搜索，然后更新非支配排序。根據(jù)支配層級(jí)順序確定麻雀種群的發(fā)現(xiàn)者、加入者和偵察者。

2.3.5 更新種群

更新了麻雀種群的發(fā)現(xiàn)者，見(jiàn)式（17）。其中，表示當(dāng)前迭代次數(shù)；X表示第個(gè)麻雀種群在第維中的位置信息（這里的遍歷發(fā)現(xiàn)者種群）；是[0, 1]之間的隨機(jī)數(shù)；max是最大迭代次數(shù)；是服從正態(tài)分布的隨機(jī)數(shù)；是元素全為1的1*維矩陣；2是麻雀種群預(yù)警值，在[0, 1]之間；T表示種群位置的安全值，在[0.5, 1]之間。當(dāng)2＜T時(shí)，預(yù)警值小于安全值，環(huán)境安全，此時(shí)發(fā)現(xiàn)者可進(jìn)行廣泛搜索操作。當(dāng)2≥T時(shí)，表示部分麻雀發(fā)現(xiàn)了捕食者，開(kāi)始向種群其他麻雀發(fā)出預(yù)警，收到警報(bào)后所有麻雀開(kāi)始飛往安全區(qū)域覓食。

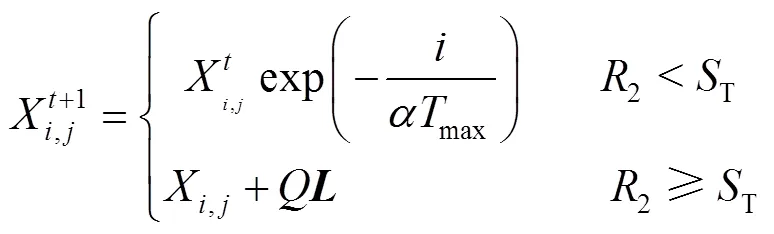
更新加入者，見(jiàn)式（18）。其中，p表示當(dāng)前發(fā)現(xiàn)者的最優(yōu)位置；worst表示全局最差位置；=TT?1，是一個(gè)1*且元素都為1或?1的矩陣；為種群數(shù)量。當(dāng)＞/2時(shí)，表示該麻雀?jìng)€(gè)體處于適應(yīng)度較差的位置。因?yàn)榭赡軙?huì)挨餓，所以需要隨機(jī)飛向其他地方覓食。

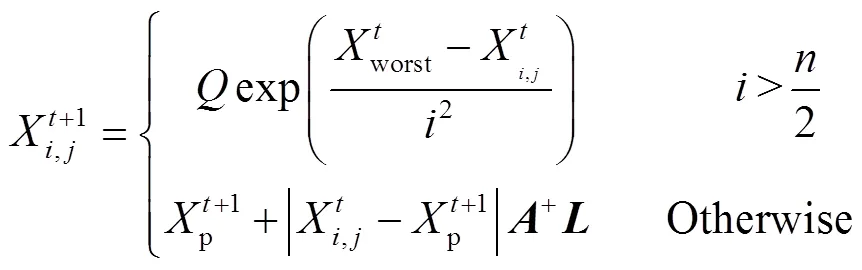
更新偵察者，見(jiàn)式（19）。其中，best是當(dāng)前全局最優(yōu)位置；是服從正態(tài)分布的隨機(jī)數(shù)，用來(lái)作為控制步長(zhǎng)的參數(shù)；是隨機(jī)數(shù)，范圍在[–1, 1]之間，同樣用來(lái)控制麻雀移動(dòng)的步長(zhǎng)參數(shù)；f是當(dāng)前麻雀?jìng)€(gè)體的適應(yīng)度值；w、g表示當(dāng)前全局最劣適應(yīng)度和全局最佳適應(yīng)度；是一個(gè)為了避免分母為0的無(wú)窮小常數(shù)。當(dāng)f＞g時(shí)，此時(shí)麻雀處在群體邊緣，容易受到捕食者的攻擊。當(dāng)f=g時(shí)，表明種群中間的麻雀意識(shí)到了危險(xiǎn)，開(kāi)始向其他麻雀靠近，從而降低被攻擊的危險(xiǎn)。

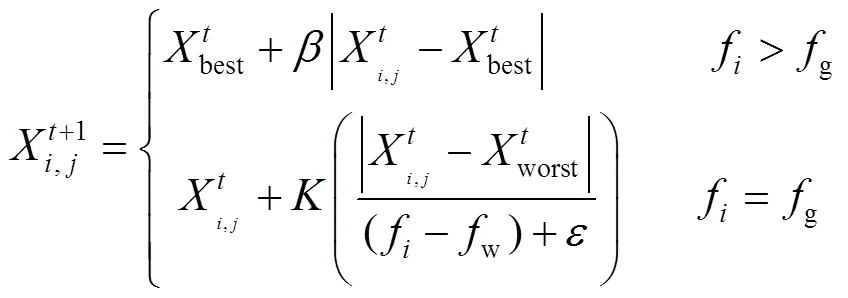
2.3.6 更新非劣解集

計(jì)算新種群P1的目標(biāo)函數(shù)值，并將最優(yōu)非劣解保存至解集Archive中，生成A1。ISSA整體實(shí)驗(yàn)流程如圖3所示，在對(duì)初始化個(gè)體的適應(yīng)度進(jìn)行非支配排序后，使用網(wǎng)格法選出最優(yōu)個(gè)體。利用爬山算法對(duì)最優(yōu)個(gè)體進(jìn)行局部搜索，產(chǎn)生新的最優(yōu)個(gè)體。對(duì)比選擇適應(yīng)度較大的最優(yōu)個(gè)體，并再次對(duì)種群進(jìn)行非支配排序。利用位置公式更新個(gè)體的位置后，計(jì)算新的種群適應(yīng)度。更新非劣解集，根據(jù)迭代次數(shù)條件判斷算法是否終止，并輸出最優(yōu)結(jié)果。

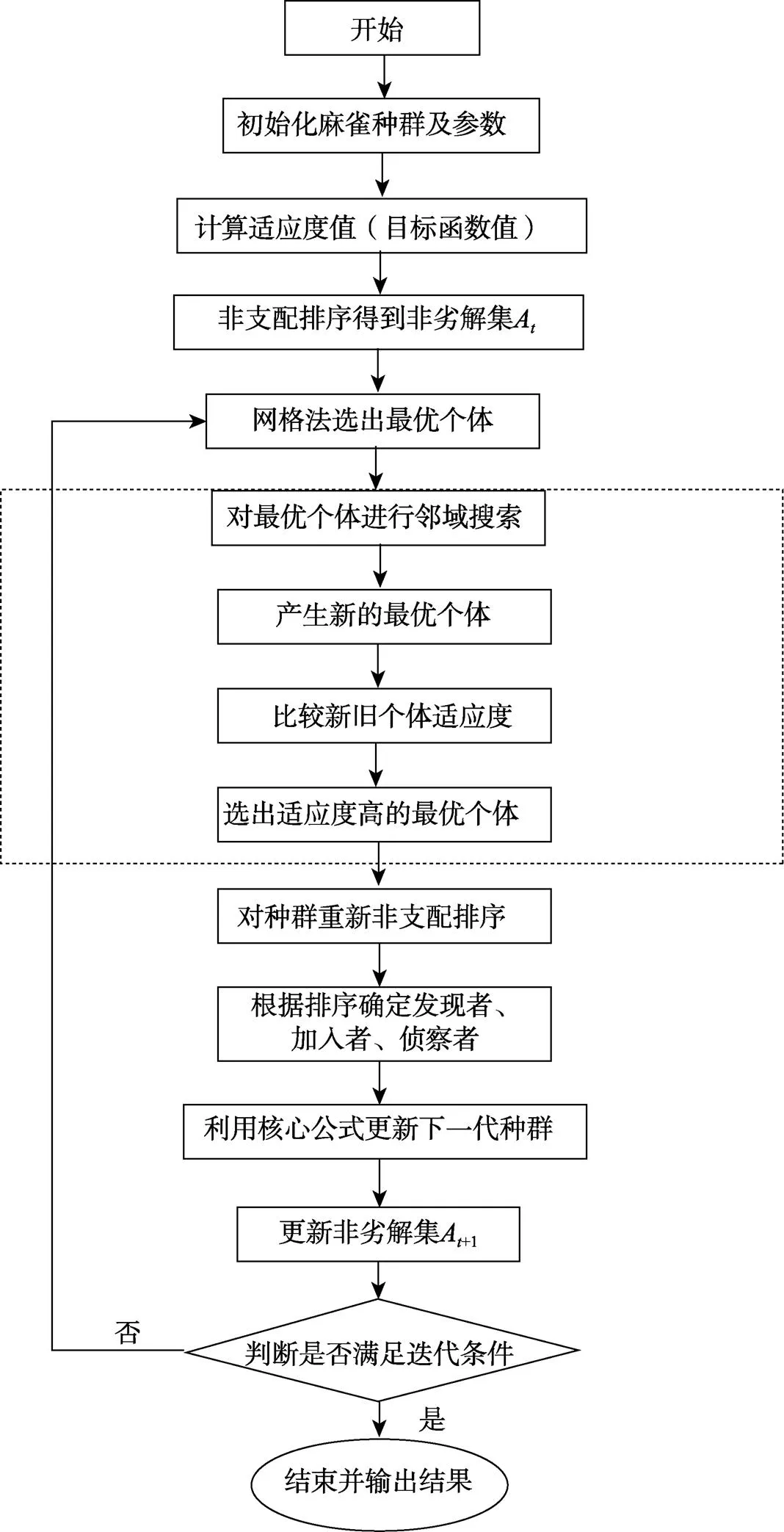
圖3 ISSA流程

3 仿真試驗(yàn)設(shè)計(jì)與分析

為了驗(yàn)證ISSA對(duì)優(yōu)化效果的提升，使用Matlab 2021a對(duì)算法進(jìn)行編程，所有程序均在一臺(tái)配置12th Gen Intel(R) Core(TM) i5-12600KF@3.70 GHz (32.0 GB)、操作系統(tǒng)為64位的Windows 10電腦上運(yùn)行。

3.1 仿真實(shí)驗(yàn)算例

為了驗(yàn)證模型的合理性和算法改進(jìn)的有效性，現(xiàn)對(duì)上海市某區(qū)域的55個(gè)需求點(diǎn)進(jìn)行冷鏈生鮮配送模擬實(shí)驗(yàn)，各點(diǎn)位置、需求量及所需時(shí)間如表1所示。結(jié)合市場(chǎng)行情及相關(guān)碳稅政策，得出模型所需參數(shù)數(shù)據(jù)，如表2所示。在表1中，編號(hào)0為配送中心，其他編號(hào)為需求點(diǎn)。

表1 小區(qū)位置、需求量及時(shí)間

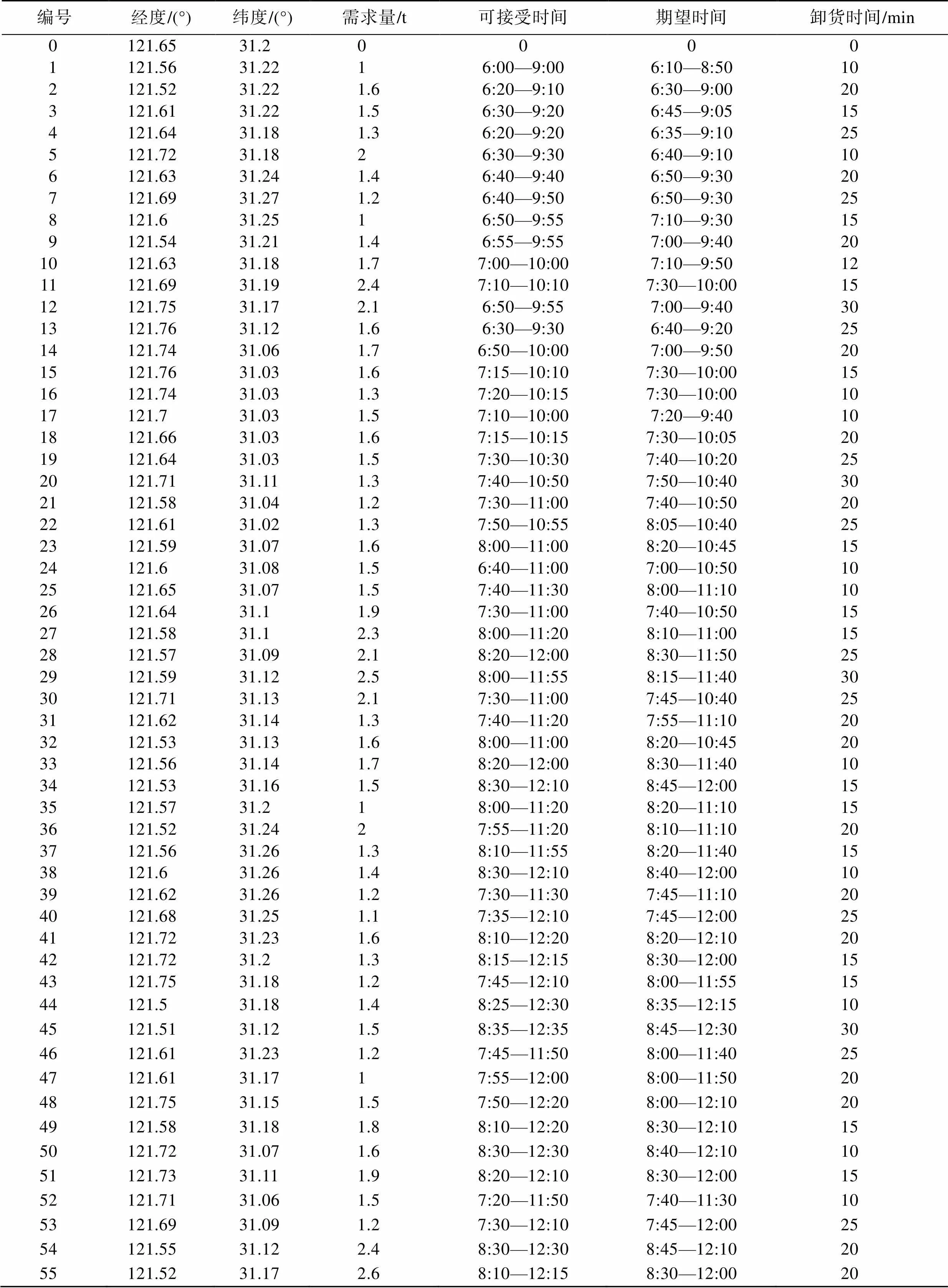
Tab.1 Community location, demand and time data

表2 模型參數(shù)取值

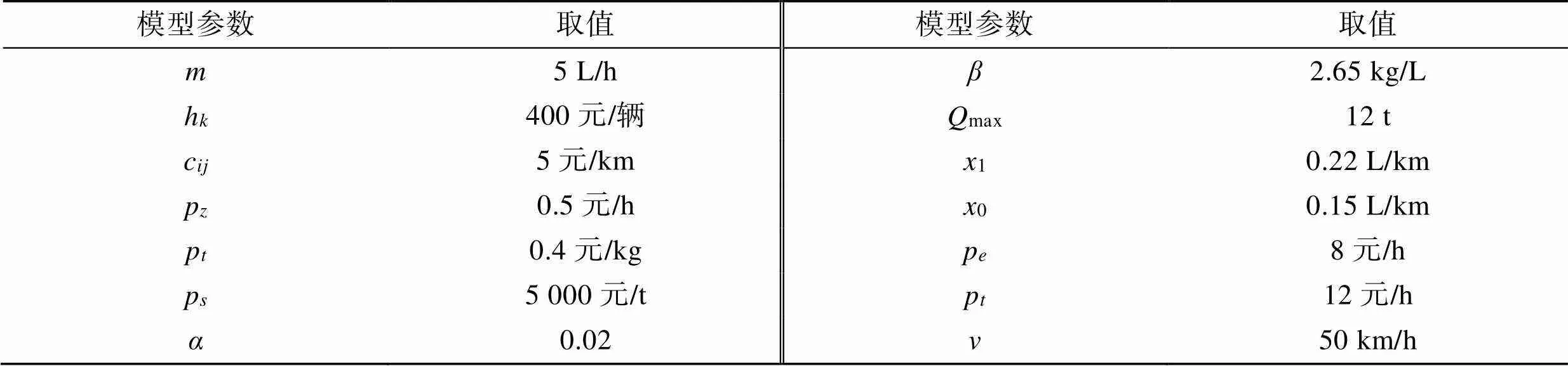
Tab.2 Model parameter value

3.2 實(shí)驗(yàn)求解結(jié)果分析

對(duì)上述算例分別使用SSA和ISSA，并借助Matlab 2021a進(jìn)行仿真求解。算法參數(shù)參考文獻(xiàn)[13]設(shè)置，麻雀發(fā)現(xiàn)者比例D=0.2，麻雀?jìng)刹煺弑壤鼶=0.1，預(yù)警值T=0.8，種群數(shù)量=80，最大迭代次數(shù)T=800。

根據(jù)表1和表2中的數(shù)據(jù)信息，對(duì)模型目標(biāo)函數(shù)進(jìn)行求解，得到最優(yōu)配送路徑，即最低成本和最大滿(mǎn)意度。使用2種算法同時(shí)對(duì)算例進(jìn)行50次求解后取均值，結(jié)果如表3所示。從表3可以看出，在相同條件下ISSA的優(yōu)化結(jié)果優(yōu)于SSA，在低成本前提下保持了較高的滿(mǎn)意度，且優(yōu)化結(jié)果標(biāo)準(zhǔn)差均小于SSA，說(shuō)明改進(jìn)后算法的運(yùn)行效果更好。

表3 ISSA與SSA實(shí)驗(yàn)結(jié)果對(duì)比

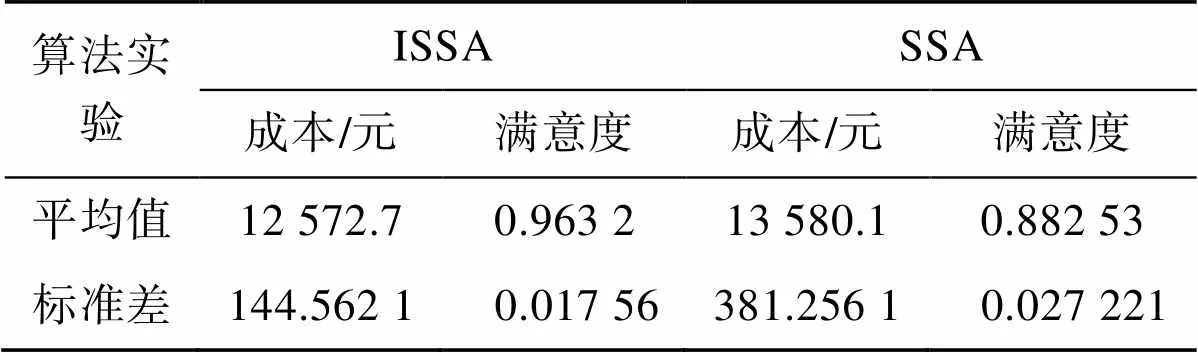
Tab.3 Comparison of ISSA and SSA experimental results

為了方便直觀地分析算法的優(yōu)化過(guò)程及結(jié)果，選取其中1次實(shí)驗(yàn)的結(jié)果。圖4和圖5分別是2個(gè)算法實(shí)驗(yàn)的成本迭代圖和滿(mǎn)意度迭代圖。可以看出，在相同的迭代次數(shù)下，ISSA相較于SSA，其收斂速度更快、效果更好；在每次算法得到最優(yōu)個(gè)體后，再對(duì)其進(jìn)行鄰域內(nèi)爬山算法搜索，這在很大程度上改善了SSA容易陷入局部最優(yōu)的缺陷，使得全局最優(yōu)結(jié)果更好。

2個(gè)算法實(shí)驗(yàn)計(jì)算結(jié)果的pareto前沿（計(jì)算結(jié)果的點(diǎn)集合不再受其他任意點(diǎn)支配）如圖6所示，總成本為軸，平均滿(mǎn)意度為軸。由于優(yōu)化要求為成本最小、平均滿(mǎn)意度最大，所以pareto前沿應(yīng)趨于左上角。從圖6中可以看出，ISSA的優(yōu)化結(jié)果pareto前沿相較于SSA更趨于左上角，所以ISSA結(jié)果整體優(yōu)于SSA。ISSA、SSA對(duì)應(yīng)的實(shí)驗(yàn)路徑優(yōu)化結(jié)果分別如圖7～8所示。

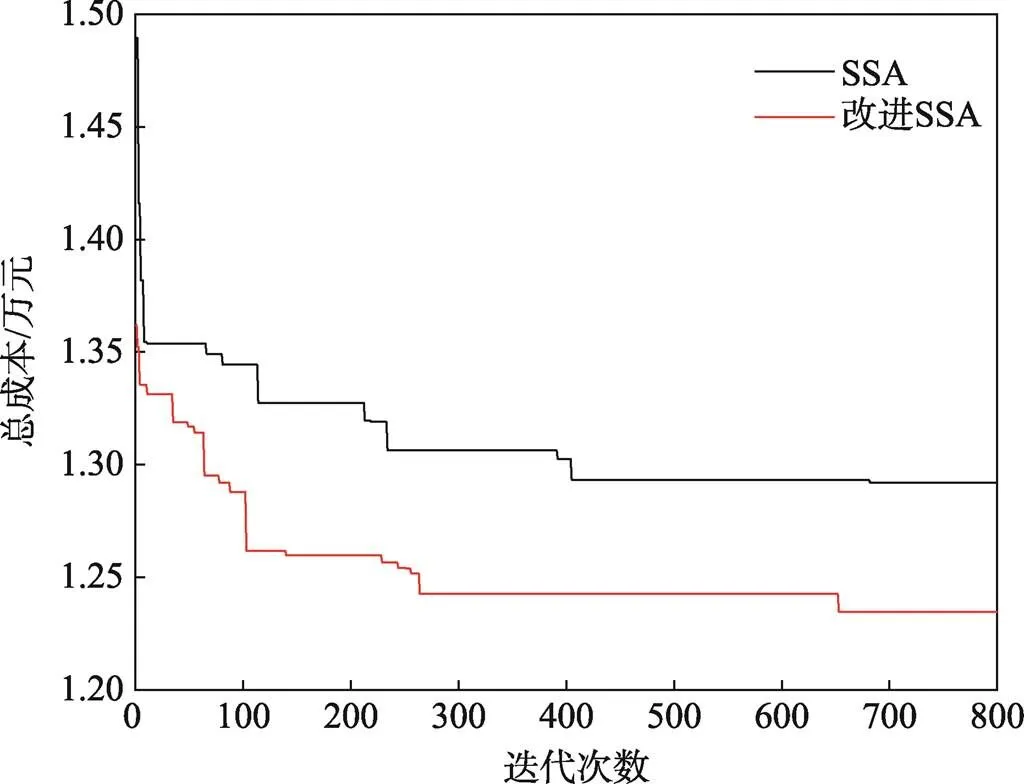
圖4 成本迭代對(duì)比

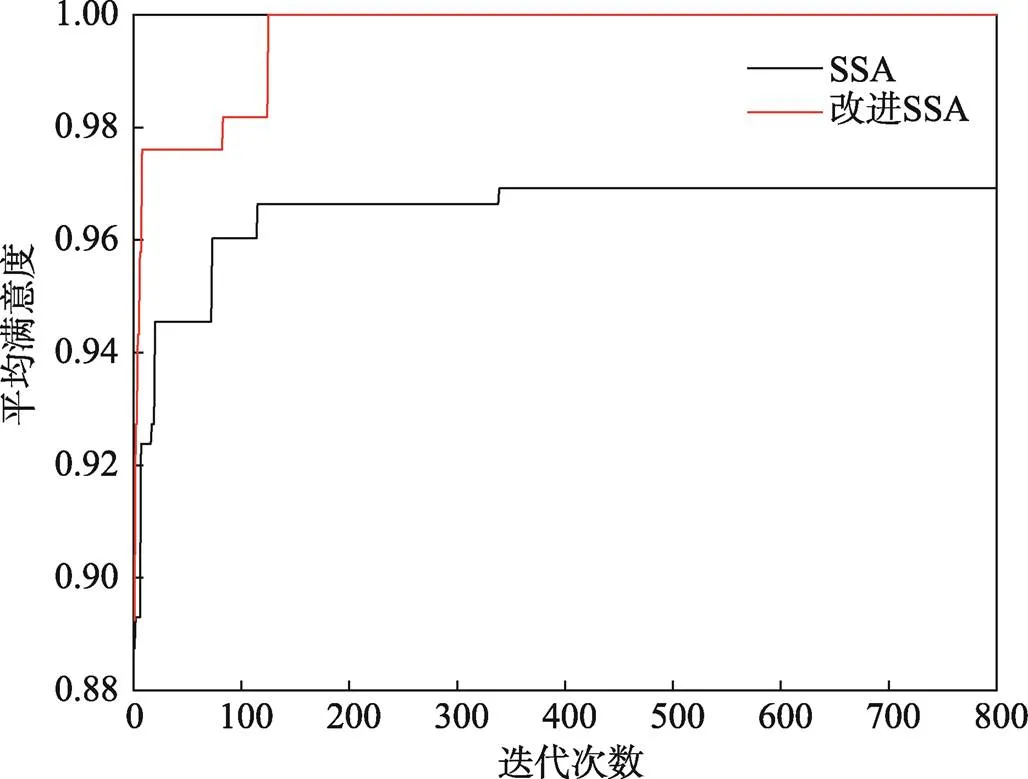
圖5 滿(mǎn)意度迭代對(duì)比

3.3 參數(shù)分析

為了驗(yàn)證算法中各參數(shù)對(duì)算法效用性的影響，需要對(duì)不同參數(shù)情況下的優(yōu)化結(jié)果進(jìn)行統(tǒng)計(jì)對(duì)比。下面主要針對(duì)不同種群規(guī)模、麻雀發(fā)現(xiàn)者比例進(jìn)行對(duì)比分析。

3.3.1 種群規(guī)模

實(shí)驗(yàn)的種群規(guī)模設(shè)置如表4所示，最大迭代次數(shù)T=800，麻雀發(fā)現(xiàn)者比例D=0.2，麻雀?jìng)刹煺弑壤鼶=0.1，預(yù)警值T=0.8，每個(gè)種群規(guī)模進(jìn)行10次實(shí)驗(yàn)，計(jì)算每個(gè)規(guī)模下10次實(shí)驗(yàn)結(jié)果的均值。

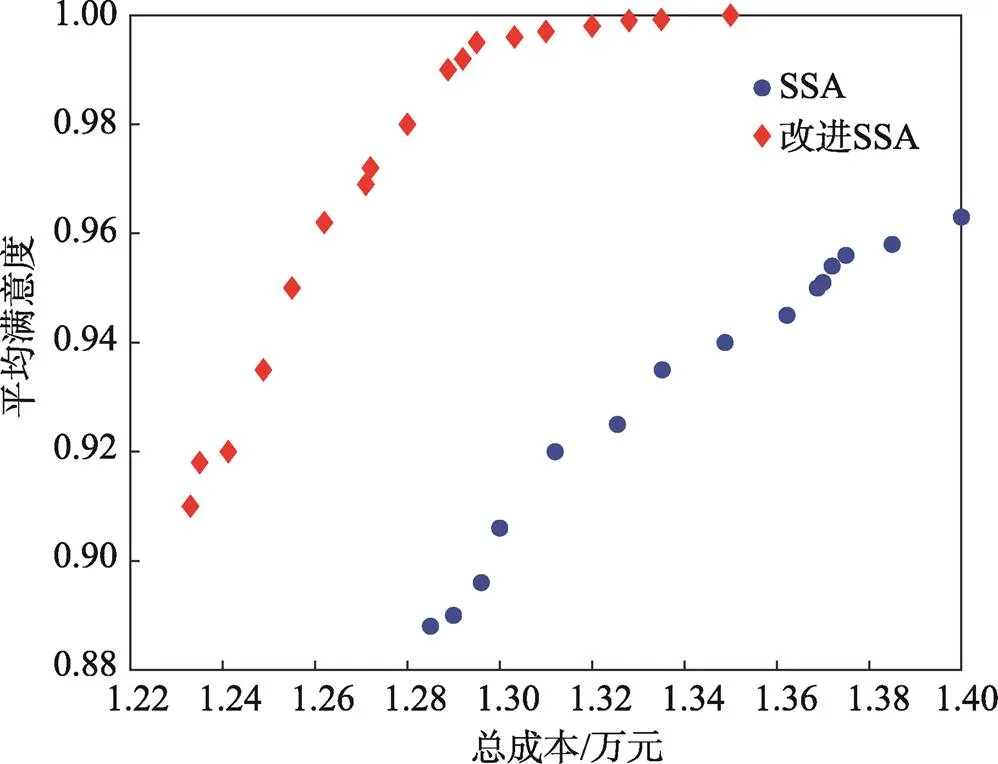
圖6 實(shí)驗(yàn)pareto前沿

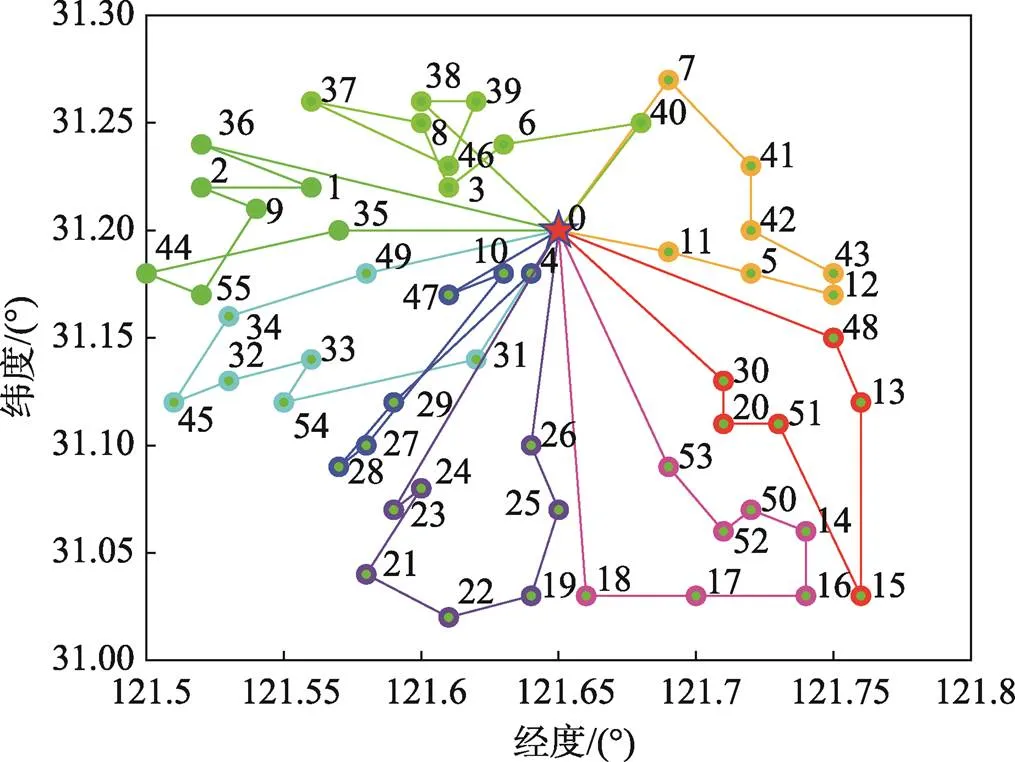
圖7 ISSA實(shí)驗(yàn)路徑

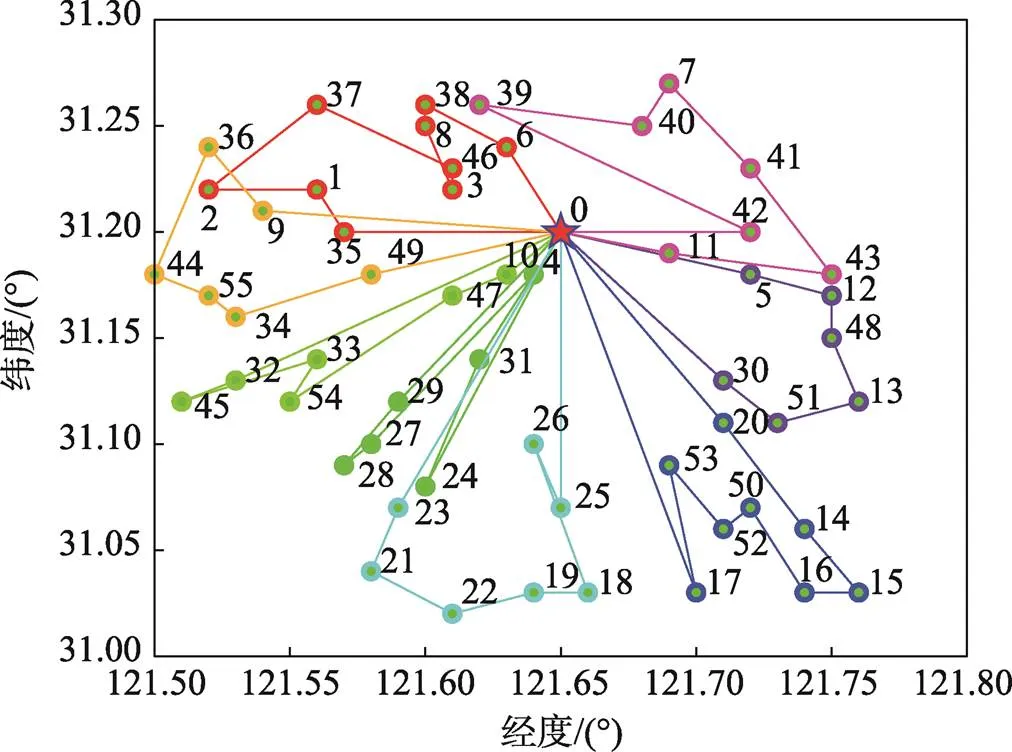
圖8 SSA實(shí)驗(yàn)路徑

由表4可知，在種群規(guī)模數(shù)量較小的情況下，ISSA不易得到最優(yōu)結(jié)果，且有一定概率出現(xiàn)優(yōu)化結(jié)果不如SSA的情況。這可能是由于種群規(guī)模較小時(shí)，麻雀種群的多樣性較低，算法缺乏局部搜索能力，導(dǎo)致全局搜索能力下降，最后陷入局部最優(yōu)解。當(dāng)種群數(shù)量在80以上時(shí)，ISSA的優(yōu)化效果較穩(wěn)定，算法優(yōu)勢(shì)也較明顯。較大的種群規(guī)模增加了種群的多樣性。在算法進(jìn)行局部搜索時(shí)，能更好地探索解空間，提高發(fā)現(xiàn)全局最優(yōu)解的機(jī)會(huì)。

表4 不同種群規(guī)模實(shí)驗(yàn)結(jié)果

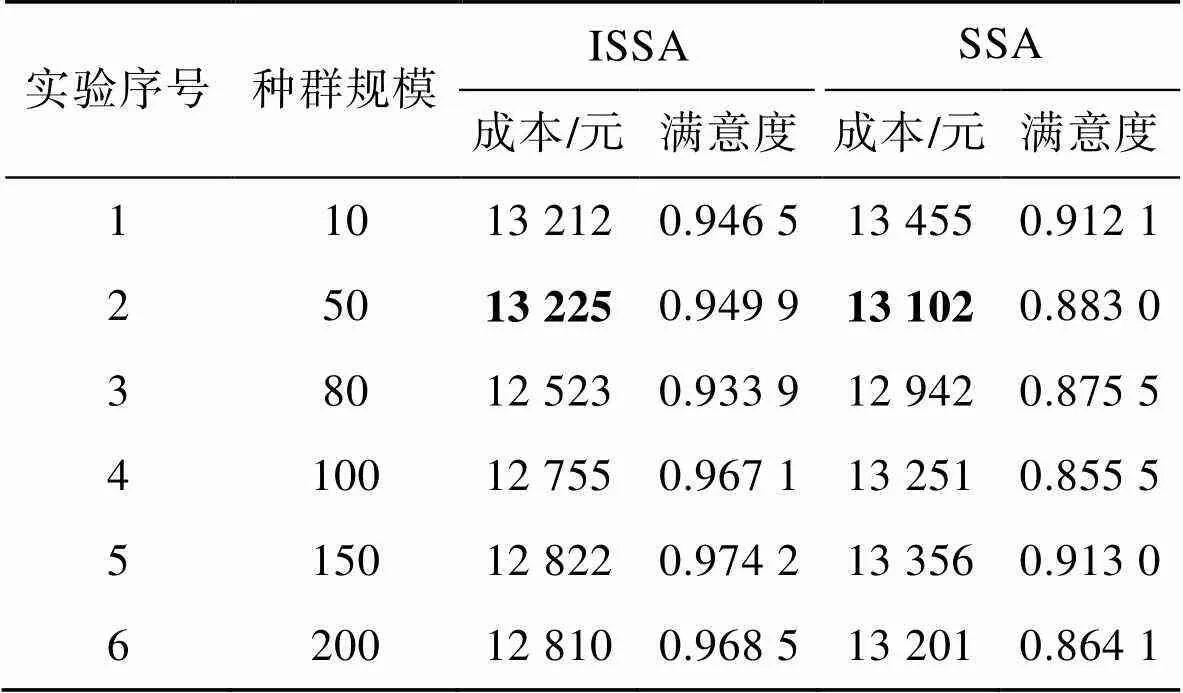
Tab.4 Experimental results of different population sizes

注：實(shí)驗(yàn)序號(hào)2加粗字體表示此次實(shí)驗(yàn)的SSA結(jié)果優(yōu)于ISSA。

3.3.2 發(fā)現(xiàn)者比例

為了驗(yàn)證麻雀發(fā)現(xiàn)者比例對(duì)優(yōu)化結(jié)果的影響，實(shí)驗(yàn)設(shè)置了不同的發(fā)現(xiàn)者比例，如表5所示，最大迭代次數(shù)T=800，麻雀?jìng)刹煺弑壤鼶=0.1，預(yù)警值T=0.8，種群規(guī)模為80。每個(gè)比例進(jìn)行10次實(shí)驗(yàn)，計(jì)算每種發(fā)現(xiàn)者比例下的10次實(shí)驗(yàn)結(jié)果的均值，并記錄算法運(yùn)行時(shí)間，如表5所示。

由表5可知，隨著發(fā)現(xiàn)者比例的增大，ISSA的優(yōu)化效果明顯改善，說(shuō)明發(fā)現(xiàn)者比例的增大可以增強(qiáng)最優(yōu)個(gè)體麻雀的搜索能力，爬山算法的融入改進(jìn)保證了每次選擇的最優(yōu)個(gè)體均不劣于原算法，提升了算法的局部搜索能力，從而提高了全局搜索的效果。SSA的效果相較于ISSA未出現(xiàn)明顯變化的趨勢(shì)，這是由于發(fā)現(xiàn)者比例過(guò)大時(shí)，SSA過(guò)分依賴(lài)全局搜索，降低了算法在局部搜索空間中的效果，符合SSA優(yōu)化效果分析得出的存在不穩(wěn)定性的結(jié)論。2種算法在發(fā)現(xiàn)者比例增大時(shí)都在一定程度上出現(xiàn)了運(yùn)算時(shí)間增加的情況，由于ISSA在每次算法流程中增加了局部搜索操作，所以相較于SSA，其花費(fèi)的時(shí)間更長(zhǎng)，但相較于優(yōu)化效果，認(rèn)為這個(gè)延長(zhǎng)的時(shí)間在可接受范圍內(nèi)。

3.4 算法效用性分析

為了進(jìn)一步分析ISSA的效用性，將ISSA與SSA、改進(jìn)鯨魚(yú)優(yōu)化算法（Improved Whale Optimization Algorithm，IWOA）[23]、改進(jìn)粒子群算法（Improved Particle Swarm Optimization，IPSO）[24]的實(shí)驗(yàn)結(jié)果進(jìn)行對(duì)比。試驗(yàn)迭代次數(shù)均為800，種群大小均為80，其余參數(shù)設(shè)置均為對(duì)應(yīng)算法的初始值。每個(gè)算法進(jìn)行20次實(shí)驗(yàn)，實(shí)驗(yàn)數(shù)據(jù)如表6。

表5 不同發(fā)現(xiàn)者比例實(shí)驗(yàn)結(jié)果

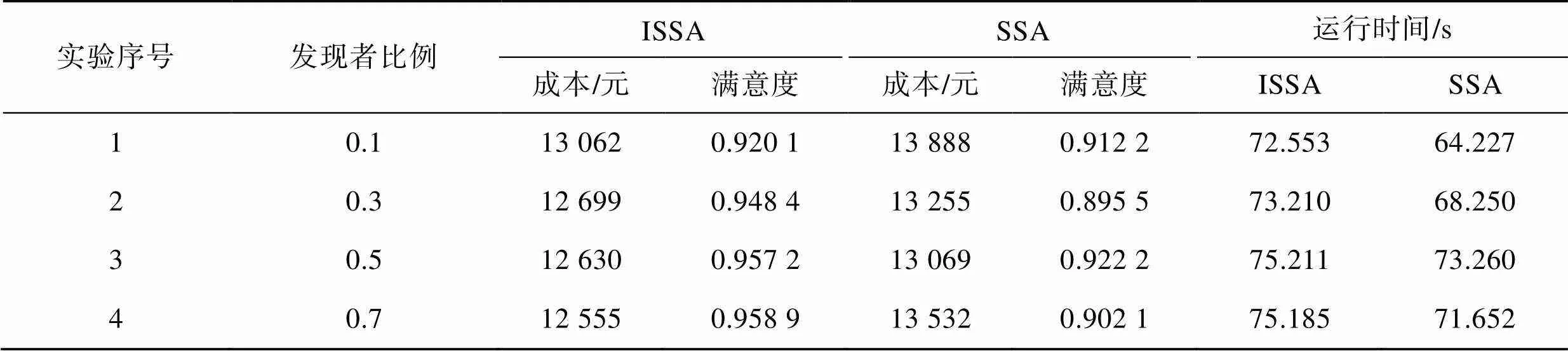
Tab.5 Experimental results of the proportion of different discoverers

表6 算法實(shí)驗(yàn)結(jié)果分析

Tab.6 Algorithm experiment result analysis

從表6可以看出，ISSA的成本和滿(mǎn)意度均值均高于其他3種算法，優(yōu)化效果最好；ISSA的標(biāo)準(zhǔn)差相對(duì)較小，算法的優(yōu)化效果較穩(wěn)定；SSA的優(yōu)化效果最差，標(biāo)準(zhǔn)差最大，優(yōu)化穩(wěn)定性較差；雖然IPSO的標(biāo)準(zhǔn)差比ISSA的標(biāo)準(zhǔn)差小，但是算法的運(yùn)行效率和優(yōu)化效果均不如ISSA，其穩(wěn)定性差距可以接受；IWOA的優(yōu)化效果和算法運(yùn)行效率接近于ISSA，但是其標(biāo)準(zhǔn)差較大、優(yōu)化穩(wěn)定性較差。為了更直觀地對(duì)比算法，取其中一次實(shí)驗(yàn)的pareto前沿圖，如圖9所示。

由圖9可知，ISSA的pareto前沿更加趨向于左上角，說(shuō)明其優(yōu)化結(jié)果更好，在相同成本的情況下可以得到更高的客戶(hù)滿(mǎn)意度。IWOA的pareto前沿有部分解跟ISSA的優(yōu)化效果近似，但是ISSA整體的pareto前沿分布相對(duì)于IWOA更穩(wěn)定。IPSO的pareto前沿分布較穩(wěn)定，且部分結(jié)果優(yōu)于IWOA，但是在成本升高時(shí)不能帶來(lái)較大滿(mǎn)意度的提升。SSA相較于其他3種算法，其優(yōu)化效果較差。

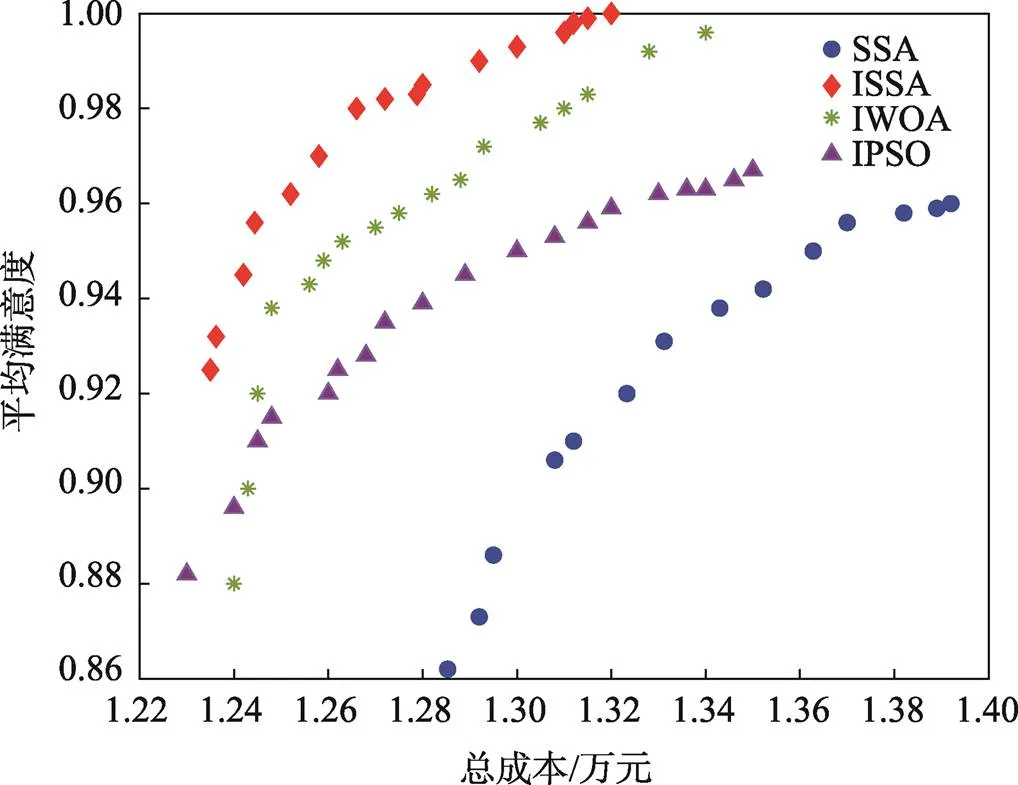
圖9 4種算法實(shí)驗(yàn)的pareto前沿

3.5 模型低碳效用性分析

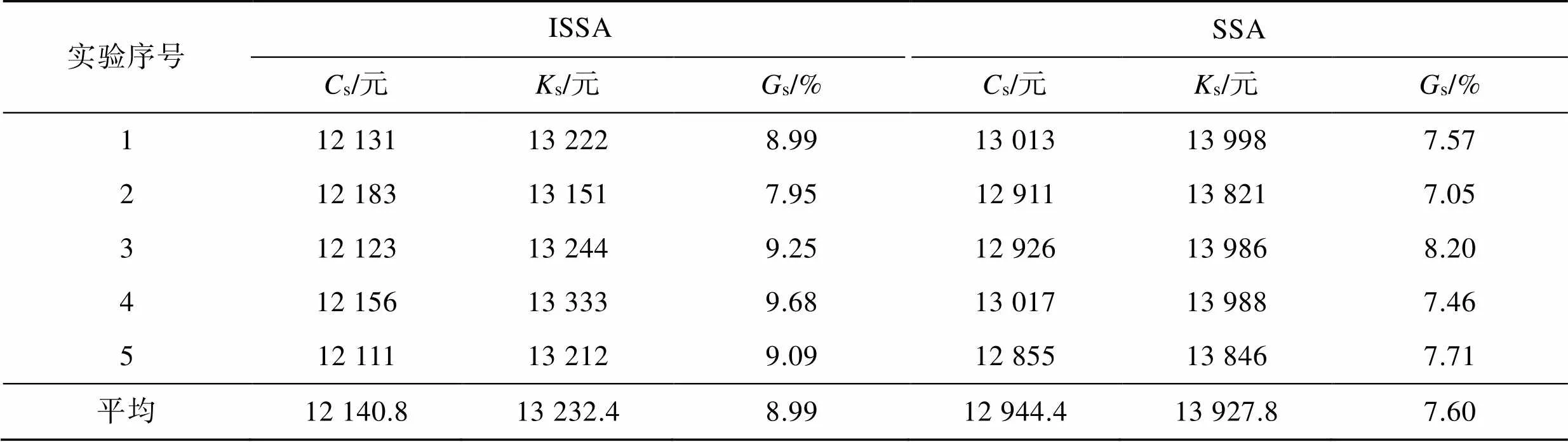
為了驗(yàn)證低碳模型能夠有效降低冷鏈物流配送的碳排放，并對(duì)整個(gè)配送網(wǎng)絡(luò)具有良好的優(yōu)化作用，將上述算例按照參考文獻(xiàn)[25]的方法進(jìn)行實(shí)驗(yàn)對(duì)比分析，將不考慮碳排放的成本結(jié)果記為s。將計(jì)算出的路徑帶入低碳優(yōu)化模型中，將結(jié)果記為s，以20次實(shí)驗(yàn)為1組，進(jìn)行5組實(shí)驗(yàn)，取每組實(shí)驗(yàn)結(jié)果的均值，再按照式（20）計(jì)算s。s通過(guò)計(jì)算計(jì)入碳稅前后的成本差占初始成本的結(jié)果比重來(lái)反映碳成本所帶來(lái)的影響，比值越大，說(shuō)明其影響越大，低碳模型的效用性越佳。

實(shí)驗(yàn)結(jié)果如表7所示，可以看出，無(wú)論采用ISSA還是SSA求解成本目標(biāo)函數(shù)，s結(jié)果平均值都達(dá)到5%以上，說(shuō)明考慮碳排放成本對(duì)ISSA和SSA優(yōu)化結(jié)果都有顯著影響，ISSA的s、s的均值均低于SSA，說(shuō)明ISSA對(duì)模型求解的效果更好；ISSA的s均值比SSA更高，說(shuō)明其模型低碳效應(yīng)性更好。

表7 低碳效用結(jié)果分析

Tab.7 Low carbon utility results analysis

4 結(jié)語(yǔ)

針對(duì)冷鏈物流的路徑問(wèn)題，結(jié)合低碳排放目標(biāo)，建立了考慮碳排放的模型，并基于傳統(tǒng)SSA對(duì)其進(jìn)行了改進(jìn)，提出了結(jié)合爬山算法局部搜索的ISSA，使得算法在原來(lái)的基礎(chǔ)上具有更好的個(gè)體最優(yōu)搜索能力，有效避免了算法陷入局部最優(yōu)的情況發(fā)生。通過(guò)ISSA、SSA、 IWOA、IPSO對(duì)實(shí)際應(yīng)用案例進(jìn)行求解，并對(duì)比分析結(jié)果，進(jìn)一步驗(yàn)證改進(jìn)算法的有效性和構(gòu)建模型的合理性。

實(shí)驗(yàn)對(duì)比結(jié)果表明，ISSA的優(yōu)化效果明顯優(yōu)于SSA，且改進(jìn)算法后運(yùn)行得更穩(wěn)定。雖然算法的改進(jìn)效果明顯，但是需要更長(zhǎng)的運(yùn)行時(shí)間，復(fù)雜度隨之略有增加。如何使算法在相同甚至更少的時(shí)間內(nèi)得到穩(wěn)定且有效的優(yōu)化還有待改進(jìn)。改進(jìn)算法使得每次迭代的麻雀最優(yōu)個(gè)體的適應(yīng)度更好，但如何針對(duì)麻雀整個(gè)種群進(jìn)行優(yōu)化，并應(yīng)用于離散優(yōu)化問(wèn)題求解，還有待研究。針對(duì)碳排放問(wèn)題建立模型，并用實(shí)際算例證明模型可以有效降低碳排放和整個(gè)配送路徑成本，未來(lái)可以進(jìn)一步將算法應(yīng)用于有特殊配送需求的VRP模型中進(jìn)行目標(biāo)優(yōu)化計(jì)算。

[1] KUEI C. Supply Chain – Logistics Management[J]. International Journal of Quality & Reliability Management, 2002, 19: 802-803.

[2] KUO J C, CHEN M C. Developing an Advanced Multi-Temperature Joint Distribution System for the Food Cold Chain[J]. Food Control, 2010, 21(4): 559-566.

[3] 丁艷. 多溫共配冷鏈物流車(chē)輛配送路徑優(yōu)化仿真[J]. 沈陽(yáng)工業(yè)大學(xué)學(xué)報(bào), 2021, 43(3): 311-316.

DING Y. Simulation of Vehicle Distribution Path Optimization for Multi-Temperature Co-Distribution Cold Chain Logistics[J]. Journal of Shenyang University of Technology, 2021, 43(3): 311-316.

[4] 李四蘭, 宋孟珂, 郭偉鈺. 基于低碳排放的冷鏈物流多溫共配路徑優(yōu)化研究[J]. 物流科技, 2021, 44(8): 152-156.

LI S L, SONG M K, GUO W Y. Study on Optimization of Multi-Temperature Co-Distribution Path of Cold Chain Logistics Based on Low Carbon Emissions[J]. Logistics Sci-Tech, 2021, 44(8): 152-156.

[5] 王淑云, 孫虹, 牟進(jìn)進(jìn). 隨機(jī)需求下蓄冷式多溫共配優(yōu)化模型[J]. 系統(tǒng)管理學(xué)報(bào), 2018, 27(4): 712-721.

WANG S Y, SUN H, MOU J J. Optimization of Cold-Storage Multi-Temperature Joint Distribution Based on Stochastic Demands[J]. Journal of Systems & Management, 2018, 27(4): 712-721.

[6] KIM G, ONG Y S, HENG C K, et al. City Vehicle Routing Problem (City VRP): A Review[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1654-1666.

[7] POTVIN J Y, BENGIO S. The Vehicle Routing Problem with Time Windows Part Ⅱ: Genetic Search[J]. INFORMS Journal on Computing, 1996, 8(2): 165-172.

[8] Br?ysy O, Gendreau M. Metaheuristics for the vehicle routing problem with time windows[J]. Report STF42 A, 2001, 1025: 3-38

[9] CORDEAU J F, LAPORTE G, MERCIER A. A Unified Tabu Search Heuristic for Vehicle Routing Problems with Time Windows[J]. Journal of the Operational Research Society, 2001, 52(8): 928-936.

[10] XUE J K, SHEN B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.

[11] 楚哲宇, 劉丹, 張蓉波, 等. 麻雀搜索算法與0-1規(guī)劃在生鮮倉(cāng)儲(chǔ)選址問(wèn)題中的應(yīng)用[J]. 自動(dòng)化應(yīng)用, 2021(9): 56-59.

CHU Z Y, LIU D, ZHANG R B, et al. Application of Sparrow Search Algorithm and 0-1 Planning in the Location of Fresh Food Storage[J]. Automation Application, 2021(9): 56-59.

[12] 阮信波, 劉麗華, 陳麗瑾. 麻雀搜索算法在物流配送中心選址的應(yīng)用[J]. 物流技術(shù), 2021, 40(12): 40-43.

RUAN X B, LIU L H, CHEN L J. Application of Sparrow Search Algorithm in Location Selection of Logistics Distribution Center[J]. Logistics Technology, 2021, 40(12): 40-43.

[13] 馮增喜, 李詩(shī)妍, 趙錦彤, 等. 基于精英反向?qū)W習(xí)策略的麻雀搜索算法[J]. 計(jì)算機(jī)仿真, 2023, 40(1): 378-381.

FENG Z X, LI S Y, ZHAO J T, et al. Sparrow Search Algorithm Based on Elite Reverse Learning Strategy[J]. Computer Simulation, 2023, 40(1): 378-381.

[14] 蘇瑩瑩, 王升旭. 自適應(yīng)混合策略麻雀搜索算法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2023, 59(9): 75-85.

SU Y Y, WANG S X. Adaptive Hybrid Strategy Sparrow Search Algorithm[J]. Computer Engineering and Applications, 2023, 59(9): 75-85.

[15] 陳登旭, 劉吉, 武錦輝, 等. 基于自閾值粒子群算法和爬山算法的DIC形變分析[J]. 國(guó)外電子測(cè)量技術(shù), 2020, 39(5): 11-16.

CHEN D X, LIU J, WU J H, et al. DIC Deformation Analysis Based on Self-Threshold Particle Swarm Optimization and Hill Climbing Algorithm[J]. Foreign Electronic Measurement Technology, 2020, 39(5): 11-16.

[16] OUYANG C T, ZHU D L, WANG F Q. A Learning Sparrow Search Algorithm[J]. Computational Intelligence and Neuroscience, 2021, 2021: 3946958.

[17] 張?zhí)烊? 劉海波. 碳稅政策下基于BFA-ACO的冷鏈物流路徑優(yōu)化[J]. 沈陽(yáng)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2022, 34(5): 363-372.

ZHANG T R, LIU H B. Cold Chain Logistics Path Optimization Based on BFA-ACO under Carbon Tax Policy[J]. Journal of Shenyang University (Natural Science), 2022, 34(5): 363-372.

[18] 曾敏剛, 王秀慧, 黎建宇. 考慮節(jié)點(diǎn)中斷與碳排放的冷鏈物流網(wǎng)絡(luò)規(guī)劃研究[J]. 華南理工大學(xué)學(xué)報(bào)(社會(huì)科學(xué)版), 2021, 23(4): 55-66.

ZENG M G, WANG X H, LI J Y. Cold Chain Logistics Network Planning Considering Node Interruption and Carbon Emissions[J]. Journal of South China University of Technology (Social Science Edition), 2021, 23(4): 55-66.

[19] 周鮮成, 蔣濤營(yíng), 賀彩虹, 等. 冷鏈物流配送的綠色車(chē)輛路徑模型及其求解算法[J]. 中國(guó)管理科學(xué),2023,31(12):203-214.

ZHOU X C, JIANG T Y, HE C H, et alGreen vehicle path model for cold chain logistics distribution and its solution algorithm[J]. Chinese Journal of Management Science:1-11.

[20] MOGHADDAM A A, SEIFI A, NIKNAM T. Multi-Operation Management of a Typical Micro-Grids Using Particle Swarm Optimization: A Comparative Study[J]. Renewable and Sustainable Energy Reviews, 2012, 16(2): 1268-1281.

[21] XI B W, LIU Z, RAGHAVACHARI M, et al. A Smart Hill-Climbing Algorithm for Application Server Configuration[C]// Proceedings of the 13th International Conference on World Wide Web, 2004: 287–296.

[22] GAO B W, SHEN W, GUAN H, et al. Research on Multistrategy Improved Evolutionary Sparrow Search Algorithm and Its Application[J]. IEEE Access, 1809, 10: 62520-62534.

[23] 陳暄, 蔡文雅. 雙目標(biāo)的冷鏈物流車(chē)輛規(guī)劃路徑的研究[J]. 現(xiàn)代信息科技, 2022, 6(23): 125-128.

CHEN X, CAI W Y. Research on the Planning Path of Cold Chain Logistics Vehicles with Dual Objectives[J]. Modern Information Technology, 2022, 6(23): 125-128.

[24] 陳智勇. 基于IPSO算法的多目標(biāo)車(chē)輛配送路徑規(guī)劃研究[J]. 山東農(nóng)業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2017, 48(2): 255-258.

CHEN Z Y. Research on Multi-Objective Vehicle Route Program Based on IPSO Algorithm[J]. Journal of Shandong Agricultural University (Natural Science Edition), 2017, 48(2): 255-258.

[25] 張坤, 張惠珍, 馬良, 等. 分布估計(jì)灰狼算法求解低碳選址路徑問(wèn)題[J]. 系統(tǒng)管理學(xué)報(bào), 2023, 32(4): 701-711.

ZHANG K, ZHANG H Z, MA L, et al. Grey Wolf Optimizer with Distribution Estimation for Low Carbon Location Routing Problem[J]. Journal of Systems & Management, 2023, 32(4): 701-711.

Improved Sparrow Search Algorithm to Solve the Routing Problem of Multi-objective Low-carbon Cold Chain Logistics Vehicle

YANG Chao, ZHANG Huizhen*,QIAN Longjun

(Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to minimize the route cost and maximize the customer satisfaction under limited resources by considering the carbon emissions generated during service nodes and vehicle transportation as well as the customer satisfaction on the basis of the traditional cold chain logistics vehicle routing problem model. A multi-objective low-carbon cold chain logistics vehicle routing problem model was constructed, and the local search idea of mountain climbing algorithm was applied to the sparrow search algorithm to form an improved sparrow search algorithm. Then, the improved algorithm was used to solve the cold chain logistics distribution path optimization problem in a certain area of Shanghai. The results were compared with the results of the other two intelligent optimization algorithms before the improvement: the improved sparrow search algorithm had faster optimization speed and better optimization ability, and the improved algorithm had higher efficiency on carbon emission of the model. Based on the national low-carbon policy, a low-carbon cold chain logistics transport model that is in line with the current situation is designed, and the transport scheme is solved by improving the optimization algorithm, which verifies the effectiveness of the local search idea of the mountain climbing algorithm on the sparrow search algorithm and the rationality of the low-carbon cold chain logistics vehicle routing model constructed.

vehicle routing problem; multi-objective;low-carbon; mountain climbing algorithm;local search; sparrow search algorithm

TP302

A

1001-3563(2024)03-0251-11

10.19554/j.cnki.1001-3563.2024.03.029

2023-04-12

國(guó)家自然科學(xué)基金（72101149）；教育部人文社會(huì)科學(xué)基金（21YJC630087）