SMA限位對鐵路自復位橋墩地震反應的影響

羅 輝，夏修身，陳琦璠，黎大瑋，張永強，馬健行

(蘭州交通大學土木工程學院,蘭州 730070)

引言

橋墩與基礎采用分離設計,在地震作用下,橋墩通過搖擺降低側向剛度,延長結構自振周期來達到隔震目的,震后靠自重實現自復位[1]。自復位橋墩強震中不會再產生塑性鉸區,避免橋墩產生嚴重破壞,可以確保震后結構的完整性,有助于快速恢復橋梁的使用功能。

最早開展結構搖擺研究的是Housner[2],Palermo等[3]開展了自復位橋梁墩柱節點的擬靜力試驗和非線性分析,并將單自由度推廣到了多自由度的整橋簡化模型。何銘華等[4]對自復位橋墩進一步完善和深化,從減小殘余應變、增加回復能力出發,提出一種新型自復位墩柱節點體系。夏修身等[5-8]先后提出兩彈簧模型和考慮限位裝置的三彈簧模型,給出了提離彈簧的恢復力模型與剛度取值方法,進行分析模型的試驗驗證,探討限位裝置對自復位橋墩搖擺反應的影響。黃麟和郭展[9-10]設計了增設高阻尼橡膠墊塊與自復位彈簧的自復位橋墩模型,進行振動臺試驗,與增設自復位彈簧的自復位橋墩相比,高阻尼墊塊降低了自復位橋墩的加速度和應力響應,有效控制墩頂水平位移。杜騫等[11]研究了自復位橋墩在近、遠場地震動高階反應,結果表明:結構第2階振型受近場地震作用的影響顯著,遠場地震動作用下墩頂水平位移更大。張哲熹等[12]研究了采用SMA拉索的搖擺自復位橋墩,討論了橋墩的滯回曲線和復位能力,研究表明:與傳統梁橋相比,采用SMA拉索橋墩可以有效降低結構殘余變形以及橋墩本身的損傷。申彥利等[13]建立了新型裝配式自復位橋墩節點的數值模型,相比傳統橋墩節點,自復位橋墩節點的承載力和耗能能力有所提升,殘余位移減小。賈俊峰等[14]建立了自復位預制拼裝RC橋墩的數值模型,探討了橋墩高寬比、預應力筋面積和初始張拉力等參數對自復位橋墩的影響。魏博等[15]研究了外置耗能器對自復位預制RC橋墩抗震性能的影響,結果表明:外置耗能器耗能段均出現明顯的高階屈曲形態,耗能作用明顯。李帆等[16]開展了外置分階段耗能阻尼器的自復位橋墩,與內置耗能鋼筋自復位橋墩相比,外置分階段耗能阻尼器自復位橋墩提高了橋墩水平承載力和橋墩初始剛度。自復位橋墩搖擺隔震效果好且穩定,但搖擺隔震可能會顯著增大墩頂位移,限位裝置可以減少墩頂位移;常規的預應力鋼筋限位會明顯增大墩底的地震彎矩,減弱自復位橋墩的隔震效果[5],且非彈性變形能力相對較弱。

SMA(形狀記憶合金)具有變形能力大、耗能能力強及自復位能力好的特點[17-18]。嘗試采用SMA進行自復位橋墩限位,并對SMA限位對自復位橋墩的影響開展系統研究。提出SMA限位單元模型,基于OpenSees建立自復位橋墩模型,探討限位位置的初始間隙和初始預加力對自復位橋墩地震反應的影響,并和預應力鋼筋限位效果進行對比。

1 基本分析數據

某單線普速鐵路橋梁,其上部采用簡支箱梁形式,橋梁計算跨徑32 m,下部結構為群樁基礎空心橋墩,其截面形式為圓端形,如圖1所示。18號墩高58 m,高墩橋梁搖擺隔震效果好且穩定,為研究SMA限位對橋墩的影響,選取18號橋墩為研究對象,墩底擴大基礎尺寸為10 m×12 m×3 m,寬度B=10 m,截面積A0=120 m2。順橋向設計時橋墩及墩底擴大基礎材料采用C30混凝土,其余參數詳見文獻[19]。

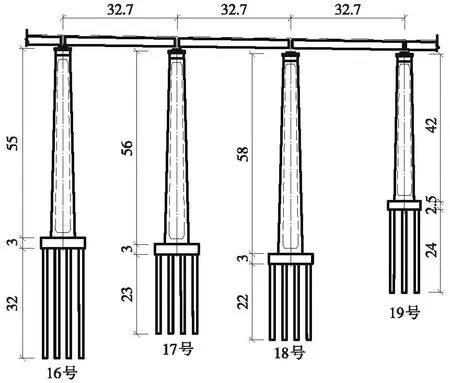
圖1 某鐵路橋墩橋梁立面布置(單位:m)Fig.1 Elevation layout of piers of a railway bridge (unit: m)

圖2中左右兩側各布置4個φ32 mm的SMA限位拉桿,每側面積A=0.003 2 m2,每根SMA拉桿長度為3 m。預應力筋限位見圖2,將SMA拉桿替換為預應力筋。

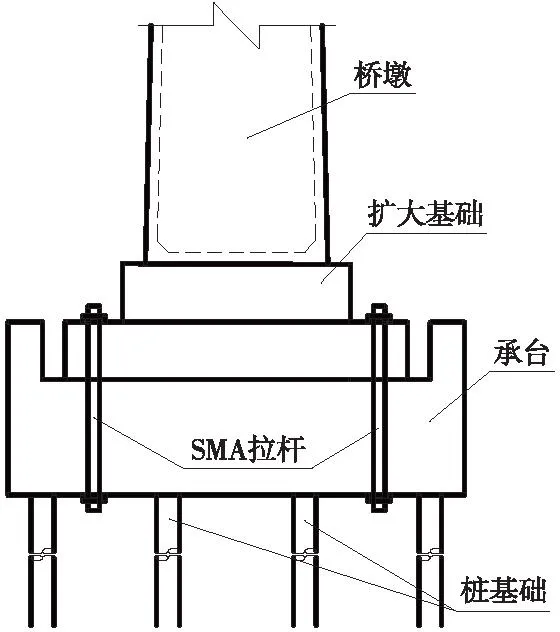
圖2 SMA限位自復位橋墩Fig.2 SMA restrainer self-centering pier

2 有限元數值分析模型

SMA限位的自復位橋墩分析模型如圖3所示。其中,墩柱、橋跨質量和橋墩的提離模擬采用文獻[6]中模擬方法。以彈性梁單元element elasticBeamColumn模擬墩柱,剛臂單元模擬墩底擴大基礎,剛臂的剛度取單元最大剛度的100倍。強震作用下,橋墩與承臺分離,發生搖擺隔震,從而墩底提離。只受壓彈簧模擬橋墩的提離,零長度單元 element zeroLength 模擬提離彈簧,模擬材料本構關系采用彈性只受壓材料uniaxialMaterial ENT,根據文獻[20],墩底提離彈簧剛度取k=2.1×108kN/m,SMA拉桿采用Self-Centering材料本構關系[21],見圖4,采用桁架單元模擬。

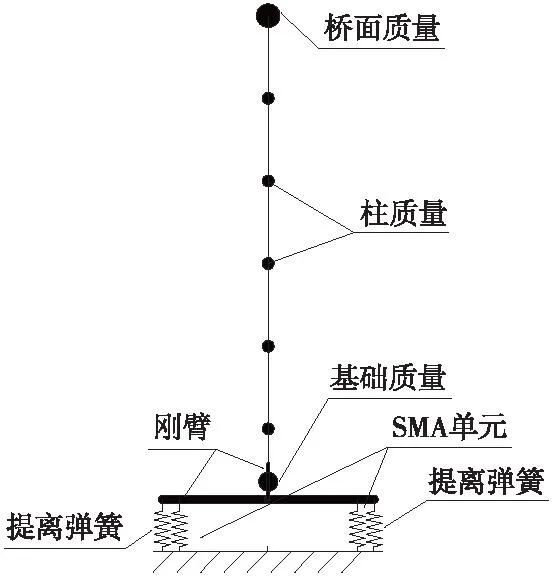
圖3 SMA限位的自復位橋墩分析模型Fig.3 Self-centering pier analysis model with SMA restrainer

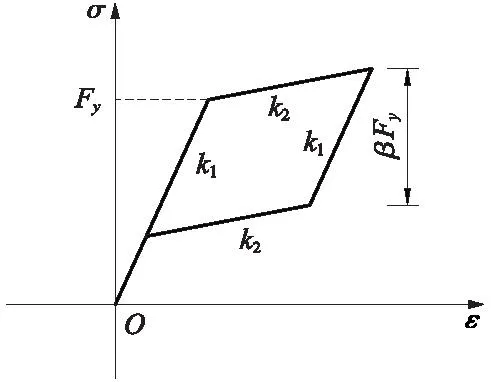
圖4 SMA材料本構關系Fig.4 Constitutive relationship of SMA material

3 初始間隙對地震反應的影響分析

為探討初始間隙δ對橋墩地震反應的影響,分別設置0,10,20,30,40 mm五組初始間隙進行分析。材料本構采用uniaxialMaterial ElasticPPGap。考慮初始間隙的SMA桿的布置、剛臂單元、零長度單元模擬方法與前文相同。

目前在OpenSees中缺少專門帶初始間隙的SMA本構模型。通過圖5和圖4的串聯實現,見圖6。圖中各參數含義為:E為彈性模量,取1.3×108kPa;δ為初始間隙;Fy為屈服應力,取3.89×107kPa;k1為材料初始剛度,取1.3×108kPa;k2為材料屈服剛度,取2.3×106kPa;β為正反向應力之比,取0.51。

圖5 uniaxialMaterial ElasticPPGap本構Fig.5 uniaxialMaterial ElasticPPGap constitutive

圖6 串聯后的SMA本構Fig.6 SMA constitutive after series

串聯后SMA本構,取k1=6.5×107kPa,k2=2.3×106kPa,Fy=3.89×105kPa,β=0.51,與文獻[21]中取值相同。

從美國太平洋地震研究中心(peer)選取3條地震波,分別為1940年El-Centro地震記錄,1994年Northridge地震記錄和1952年Taft地震記錄,見表1。

表1 地震動輸入信息Tab.1 Ground motion input information

5組初始間隙的墩頂水平位移與墩底彎矩地震反應列于表2,典型時程曲線如圖7～圖9所示。

圖7 墩頂水平位移時程曲線(El-Centro)Fig.7 Time-distance curve of horizontal displacement at the top of the pier (El-Centro)

El-Centro地震動作用下,初始間隙δ=40 mm時,由于初始間隙較大,SMA拉桿基本未起到限位作用,此時橋墩的地震反應接近沒有限位的自由搖擺。由圖7、圖8可以看出,SMA限位中的曲線與自由搖擺的曲線形狀吻合較好(這說明當前設計的限位裝置基本沒有改變自由搖擺橋墩的動力特性),再結合表2可知兩者僅在最大值處略有差異。

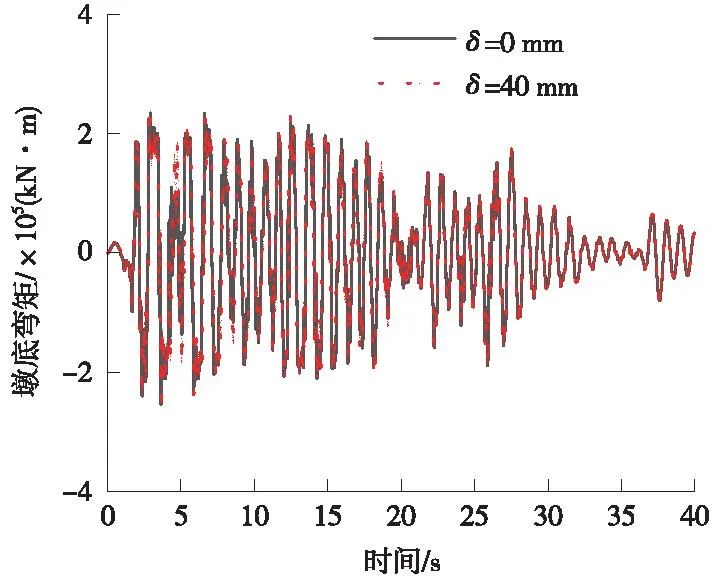
圖8 墩底彎矩時程曲線(El-Centro)Fig.8 Time-distance curve of bending moment at the base of the pier (El-Centro)

由圖9可以看出,El-Centro地震作用下,初始間隙δ=10 mm時,SMA限位拉桿已進入屈服耗能階段,但耗能能力尚未充分發揮。

圖9 SMA滯回曲線(El-Centro)Fig.9 SMA hysteresis curve (El-Centro)

由表2可知,不同初始間隙下3條地震波下的地震反應有一定離散性,其中Northridge波下的反應遠大于EL-Centro波與Taft波,這是因為Northridge波是近斷層地震動,而El-Centro波與Taft波是普通地震動。δ從30 mm 逐漸減小到0 mm,墩頂水平位移也隨之減小,這是因為初始間隙大的SMA拉桿需要更大的應變才能屈服。δ=40 mm與δ=0 mm相比,El-Centro作用下墩頂水平位移減少1%;Taft波作用下,墩頂水平位移基本沒變,這是因為初始間隙δ=40 mm時,SMA拉桿未起到限位作用,所以水平位移基本保持不變。Northridge波作用下,墩頂水平位移增大4%。

由表2還可知,δ從40 mm減小到0 mm,El-Centro作用下墩底彎矩增大3%;Taft波作用下,墩底彎矩增大1%;Northridge波作用下墩底彎矩減小3%。

4 初始預加力對地震反應的影響分析

18號墩底恒載的豎向力之和為37 599 kN。為探討初始預加力的影響,取初始預加力分別為豎向力的0%,1%,2%,3%,4%。SMA桿面積布置及長度與前文相同,采用uniaxialMaterial InitStrainMaterial命令施加初應變來實現施加初始預加力,根據文獻[20]初應變按下式計算

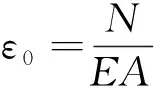
(1)

墩頂水平位移見圖10,墩底彎矩見圖11,SMA滯回曲線見圖12。

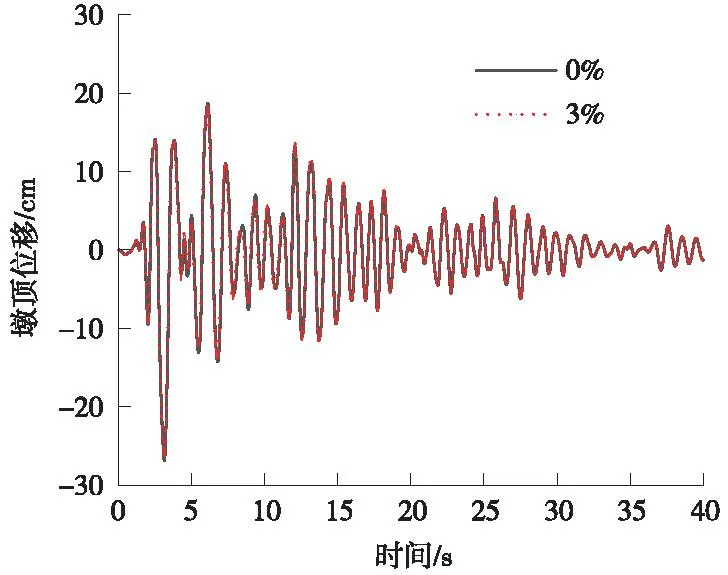
圖10 墩頂水平位移時程曲線(El-Centro)Fig.10 Time-range curve of horizontal displacement at the top of the pier (El-Centro)

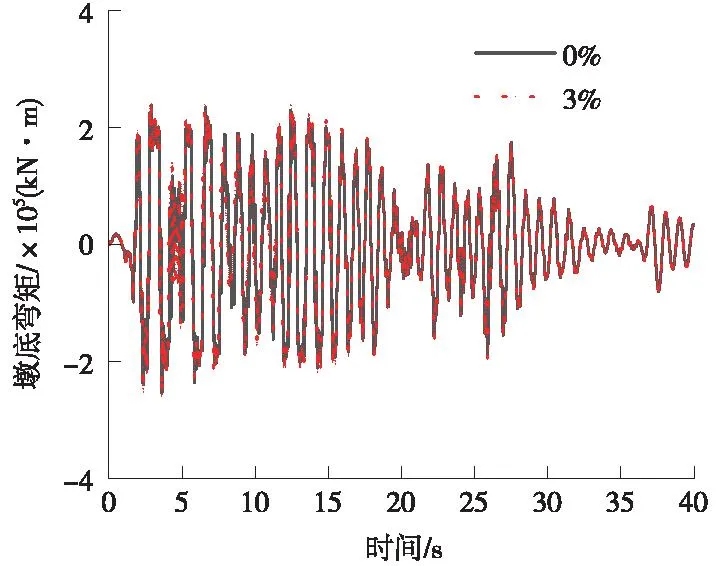
圖11 墩底彎矩時程曲線(El-Centro)Fig.11 Time-dependent curve of bending moment at the base of the pier (El-Centro)

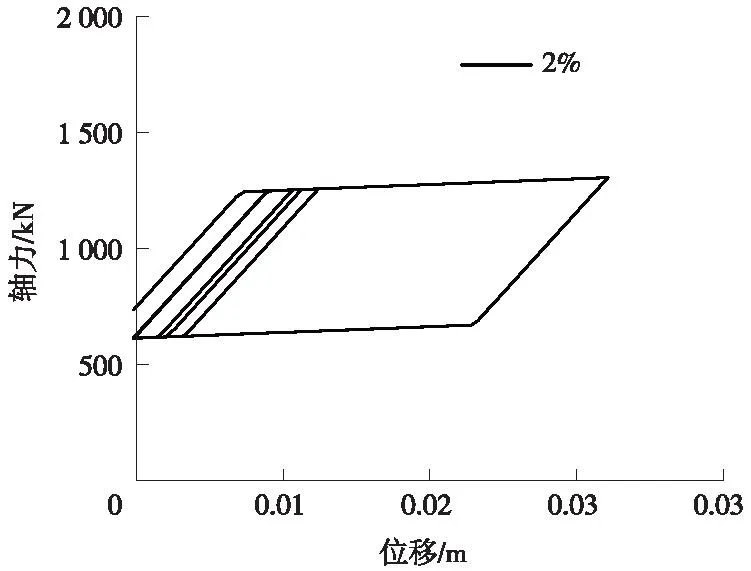
圖12 SMA 滯回曲線(El-Centro)Fig.12 SMA hysteresis curve (El-Centro)

從圖10可以看出,El-Centro波作用下,豎向力3%的初始預加力與無初始預加力的墩頂水平位移吻合較好,只有最大值有所減小。

從圖11可以看出,El-Centro波作用下,在0～5 s時間段,豎向力3%初始預加力的墩底彎矩大于無初始預加力的墩底彎矩,其他時間段吻合較好。

SMA拉桿屈服應力為3.89×105kPa,對應SMA拉桿的屈服力為1245 kN,初始預加力為豎向力的4%,初始預加力大于屈服力,此時SMA拉桿已經屈服失效。由圖12可以看出,預加力為豎向力2%,此時SMA拉桿已經屈服,發揮了耗能能力。

不同初始預加力地震反應比較見表3,可以看出,預加力減小了墩頂水平位移。隨著初始預加力增大,El-Centro波作用下墩頂水平位移減小1%。Taft波作用下位移減小6%,Northridge波作用下位移減小1%。隨著初始預加力增大,El-Centro波作用下墩底彎矩增大2%,Taft波作用下墩底彎矩增大4%,Northridge波作用下墩底彎矩增大3%。

表3 不同初始預加力地震反應比較Tab.3 Comparison of seismic responses with different initial prestress

5 SMA限位與預應力筋限位對比分析

為使SMA拉桿與預應力筋屈服,將選取的3條地震波的地震動幅值統一調整為0.57g,輸入方向為順橋向的水平方向。預應力筋剛度及面積與SMA拉桿相同,為A=0.003 2 m2,布置與前文SMA布置相同,無初始間隙和初始預加力,預應力鋼筋采用文獻[20]中的方法模擬,設置以下3種工況進行分析。工況1—自由搖擺、無限位裝置;工況2—預應力鋼筋限位的受控搖擺;工況3—SMA限位的受控搖擺。在El-Centro波下,橋墩的典型搖擺反應時程曲線如圖13～圖16所示。3種工況下墩頂水平位移、墩底彎矩以及豎向提離位移地震反應見表4。

表4 3種工況地震反應分析Tab.4 Seismic response analysis for 3 working conditions

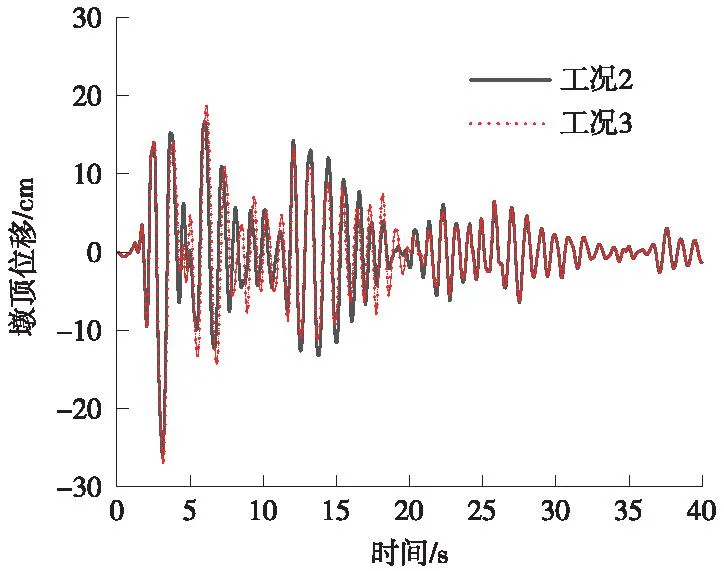
圖13 墩頂水平位移時程曲線(El-Centro)Fig.13 Time-range curve of horizontal displacement at the top of the pier (El-Centro)

由圖13可知,在0～5 s,墩頂水平位移最大,同時工況3墩頂位移大于工況2;在5～10 s時間段,工況3墩頂水平位移大于工況2,在10～20 s時間段,工況3墩頂位移小于工況2,限位裝置起到限位的作用。其他時間段工況3和工況2吻合較好,這是因為預應力鋼筋的彈性模量比SMA的彈性模量大,所以預應力筋限位的墩頂位移比SMA桿限位的小。

從圖14可以看出,0～5 s和15～20 s時間段,工況3墩底彎矩小于工況2,SMA限位相對于預應力筋限位,減小了墩底彎矩。其他時間段,工況3和工況2曲線吻合較好。

圖14 墩底彎矩時程曲線(El-Centro)Fig.14 Time-distance curve of bending moment at the base of the pier (El-Centro)

結合圖15及表4可知,SMA限位的受控搖擺與自由搖擺相比,SMA限位減少了橋墩的提離位移和提離次數;與預應力鋼筋限位相比,提離位移限位稍差。

圖15 橋墩基礎的提離位移(El-Centro)Fig.15 Lift-off displacement of pier foundation (El-Centro)

由圖16可知,El-centro波,工況3比工況2拉力小,這是因為SMA桿的屈服力小于預應力筋的屈服力。

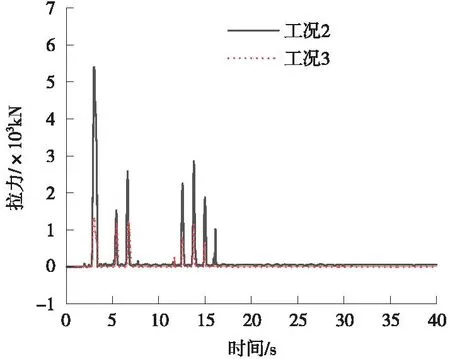
圖16 限位裝置拉力時程曲線(El-Centro)Fig.16 Restrainer device tension time curve (El-Centro)

表4可以看出,SMA限位比自由搖擺的自復位橋墩墩底彎矩大,這是因為SMA增大了橋墩的初始提離彎矩,而墩底彎矩與初始提離彎矩有關。SMA限位墩底彎矩比預應力筋限位的墩底彎矩小,這是因為SMA拉桿的耗能能力比預應力筋強。在El-centro波下,和自由搖擺相比,工況2的墩底彎矩增大6%,工況3增加3%。由圖13和表4可知,墩頂水平位移工況2減小5%,工況3減小2%。

將計算結果與文獻[5]和文獻[20]進行對比,計算結果可靠。

6 結論

(1)提出了自復位橋墩中只受拉不受壓的SMA限位裝置模擬方法,且能考慮初始間隙與施加初始預加力。

(2)在普通地震動El-Centro與Taft作用下,隨著限位裝置初始間隙減小,SMA限位的自復位橋墩墩頂位移減小,墩底彎矩增大。在近斷層地震動Northridge波下則不具有這一規律。

(3)隨著限位裝置初始預加力增大,SMA限位的自復位橋墩墩頂位移減小,墩底彎矩增大。

(4)SMA限位和自由搖擺相比可以減小橋墩頂部水平位移,減小提離位移和提離次數,但會增大墩底彎矩。與預應力鋼筋限位相比,SMA限位的墩頂位移限位效果稍差,但不會顯著增大墩底彎矩。