基于期望任務壽命的可重復運載火箭RMT參數規劃模型研究

李彩霞，彭 越，方志耕，賀元軍，劉樹仁

(1. 北京宇航系統工程研究所，北京 100076；2. 南京航空航天大學，南京 210018；3. 中國載人航天工程辦公室，北京 100083)

0 引言

為了減小火箭的發射成本，各個國家開始發展可重復使用運載器(Reusable Launch Vehicle，RLV)。RLV是指火箭完成任務后，將其箭體安全著陸到預定落點，維修后仍然可以繼續使用，從而有效地降低發射費成本，提高發射效率。自20世紀中期人類提出RLV的概念以來，RLV一直都是世界各國的研究熱點[1-12]。在可重復運載火箭的高可靠性背景下，可靠性維修性測試性(RMT)相關指標的設計與參數規劃顯得尤為重要，為此本文針對基于期望任務壽命的可重復運載火箭RMT指標進行參數規劃，通過綜合運用馬爾柯夫等多種理論，解析可重復運載火箭的發射過程，建立重復使用運載火箭RMT指標模型并進行參數設計等，為重復使用運載火箭可靠性研制提供參考。

1 基于RMT可重復運載火箭的穩態可用度解析模型設計

1.1 可重復運載火箭發射與維修過程解析

可重復運載火箭發射過程與維修過程以第一次發射為例進行解析。

(1)發射任務的可靠度變化解析

假設可重復運載火箭一次發射前可靠度為R1.0，發射任務過程中，失效率為λ1.0，由于運載火箭發射過程無法進行維修，得到發射后可靠度R1.1與發射前可靠度關系如式(1)所示

R1.1=R1.0(1-λ1.0t)R

(1)

其中t為任務時間。

(2)發射回收后的維修過程解析

可重復運載火箭第一次發射任務結束，返回并回收后，將進行故障檢測與維修，然后再發射。假設綜合故障檢測率為D*.0檢測綜，綜合檢測率D*.0檢測綜是由關鍵故障檢測率D*.0關鍵和非關鍵故障檢測率D*.0非關鍵串聯得到，其中關鍵故障的檢測率為1-1×10-7(參考飛機等相關復雜裝備的指標要求，并考慮可重復運載火箭的實際情況)，非關鍵故障檢測率為0.99(理由同D*.0關鍵暫取指標)(見圖1)，其公式如式(2)所示

D*.0檢測綜=D*.0關鍵×D*.0非關鍵

(2)

根據關鍵故障檢測率和非關鍵故障檢測率可以得到綜合檢測率為

D*.0檢測綜=D*.0關鍵×D*.0非關鍵

=(1-1×10-7)×0.99

=0.989 999 901

≈0.99

(3)

根據每次發射后維修的任務性質，對維修度參數M1.0維修綜進行設計，根據檢測率D1.0檢修綜與維修度M1.0維修在保證火箭可用性A過程中遞進的串聯邏輯關系(見圖2)，構建綜合維修度M1.0維修綜=D1.0檢測綜×M1.0維修，根據維修率與維修度的關系可以求出綜合維修率μ1.0維修綜。

可重復運載火箭之后的發射過程與第一次發射過程類似，其中維修度以及維修率會根據每次發射后維修程度(如大修和小修)等有所不同，其余基本相同，如圖3所示。

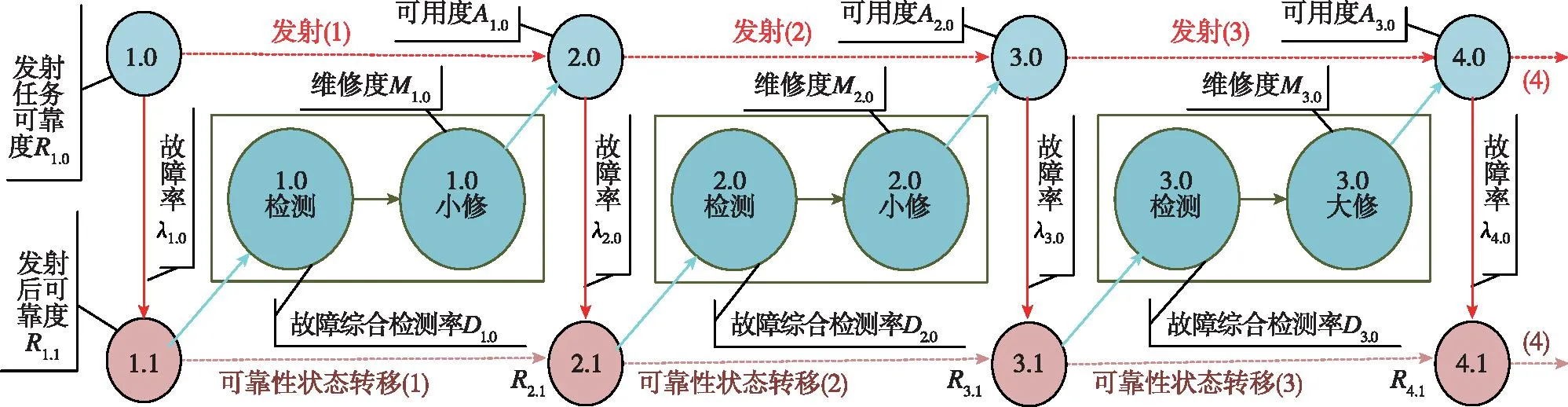
圖3 可重復運載火箭發射與維修關系示意圖Fig.3 Schematic diagram of the relationship between launch and maintenance of reusable launch vehicle

1.2 可重復運載火箭一次發射任務過程RMT模型設計

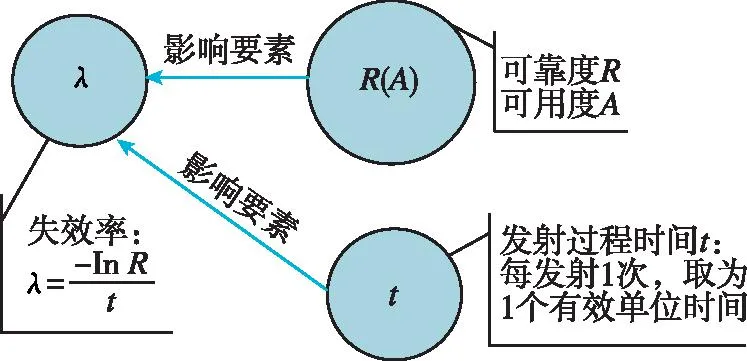
圖4 可重復運載火箭失效率要素結構關系示意圖Fig.4 Schematic diagram of structural relationship of failure rate factors of repeatable launch vehicle

根據重復發射與維修之間的相互關系，由失效率可推導出相關指標要素，它們之間的結構關系(以第一次發射過程為例)如圖5所示。發射與維修過程的指標如下。

圖5 可重復運載火箭失效率與相關指標結構關系示意圖Fig.5 Schematic diagram of structural relationship between failure rate and related index of repeatable launch vehicle

(1)發射前可靠度R1.0

以第一次發射為例，發射前可靠度R1.0由其任務飛行過程失效率λ1.0和飛行任務時間t1.0決定，關系如式(4)所示

R1.0=e-λ1.0t1.0

(4)

(2)發射后維修前的可靠度R1.1

以第一次發射為例，在發射任務要求可靠度為R1.0的情況下，經過t1.0時間后，發射后維修前的可靠度下降到R1.1，如公式(5)所示

R1.1=R1.0×(1-λ1.0t1.0)

(5)

(3)發射后維修后的可用度A1.0

以第一次發射為例，發射回收并維修后的可用度與失效率的關系如公式(6)所示

(6)

即可用度A1.0是由維修綜合維修率μ1.0維修綜和失效率λ1.0共同決定的，表明經過維修后，其可用度達到A1.0，該可用度即為第二次發射前的任務可靠度R2.0，即R2.0=A1.0。

(4)綜合維修率

發射結束、回收后進行故障檢測，其故障檢測率為D檢測綜，并對檢測到的故障進行維修，其綜合維修度為M維修綜，根據綜合維修度公式(7)

M維修綜=D檢測綜×M維修=1-e-μ維修綜t綜

(7)

其中，t綜為綜合維修時間，μ維修綜為綜合維修率μ維修綜。

1.3 一次發射過程可靠性狀態馬爾可夫穩態分析

假設：表示發射前的初始可靠性狀態，初始狀態概率矩陣為

(8)

其中，*代表是第*次發射，R*.0為第*次發射前的可靠度，1-R*.0為不可靠度。

由狀態轉移可以得到狀態轉移概率矩陣P，如圖6所示。矩陣P表示一次發射后的馬爾可夫狀態轉移矩陣，飛行過程中沒有維修過程，所以在該矩陣中，不考慮維修，即狀態2為吸收狀態，狀態轉移到2狀態(待維修狀態)后，將不再轉移到1狀態(正常工作狀態)，所以此時維修部分應取維修率為0。

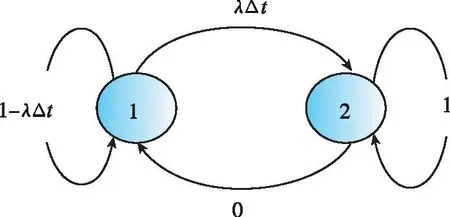
圖6 發射過程(維修前)可靠性狀態轉移圖Fig.6 Reliability state transition diagram during launch (before maintenance)

(9)

火箭發射一次后，即由初始狀態經過狀態轉化計算得到發射后狀態轉移概率矩陣

P(1)=Q(0)P

=(R*.0(1-λΔt)R*.0λΔt+1-R)

(10)

式(10)的矩陣中，R*.0(1-λΔt)表示一步轉移后(一次發射完成后，未維修時)火箭的可靠度。R*.0λΔt表示可靠度的降低值，即一次發射完成后，可靠度降低了R*.0λΔt。

發射一次后火箭的可靠度降低為

R*.1=R*.0(1-λΔt)

(11)

其中，R*.1為第*次發射后維修前的可靠度。

1.4 一次發射回收經過維修后能夠達到的穩態可用度模型構建

一次發射回收后，馬爾可夫狀態轉移表示為

(12)

其中，“1”狀態表示運載火箭的正常工作狀態，“2”狀態表示運載火箭的待維修狀態，以X(t)表示t時刻系統狀態。

圖7是狀態轉移圖，也稱馬爾可夫圖或夏農圖。由狀態轉移圖得狀態轉移矩陣

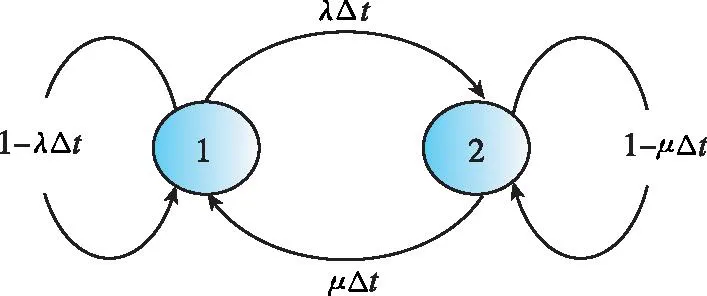
圖7 發射過程(考慮綜合維修情況)馬爾可夫狀態轉移圖Fig.7 Markov state transition diagram of launch process (considering comprehensive maintenance)

(13)

1.4.1 瞬態可用度推導

設在t時刻，系統處于正常工作狀態的概率為P1(t)，處于待維修狀態的概率為P2(t)，則系統在t+Δt處于1態(正常工作狀態)的可能狀態轉移概率是由兩個可能事件的概率組成的：

1)系統在t時刻保持在1態，即正常工作狀態，經Δt時間后，若失效率為λ，則故障概率為λΔt，保持正常工作的概率為1-λΔt。

2)系統在t時刻處于2態，即待維修狀態，經過時間Δt后，修復為1態，若維修率為μ，則轉移到正常工作的概率為μΔt。此時可得方程式

P11(Δt)=P{X(t+Δt)

=1|X(t)=1}

=1-λΔt+0(Δt)

(14)

P21(Δt)=P{X(t+Δt)=1|X(t)=2}

=μΔt+0(Δt)

(15)

所以有

P1(t+Δt)=P1(t)P11(Δt)+P2(t)P21(Δt)

(16)

取極限令Δt→0后，整理可得

(17)

同樣可得2狀態的方程為

(18)

利用拉氏變換可以解微分方程

(19)

1.4.2 穩態可用度推導

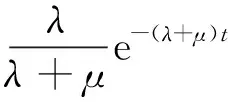
(20)

2 基于期望任務壽命的可重復運載火箭RMT指標規劃

2.1 基于RMT的可重復運載火箭發射規劃與參數設計

2.1.1 發射規劃

可重復運載火箭(特指運載火箭中的一級回收火箭(下同))執行任務過程可分為點火發射過程、正常運行過程、回收過程、測試診斷過程、維修過程、后進入再發射過程。本文暫假設期望發射次數(壽命)為10次。

若可重復運載火箭發射與回收的目標任務按照10次的期望次數(壽命)進行設計，考慮執行任務輪數可以分為3輪，每次回收后均需要進行檢測與維修后再發射，具體發射次數與維修過程初步安排見圖8。

圖8 期望發射次數(壽命)為10次的發射過程分析示意圖Fig.8 Schematic diagram of launch process analysis with expected launch times (lifetime)of 10

每一輪第一次發射后(第二次發射前)將會有一次小修，第二次發射后(第三次發射前)仍將會有一次小修，第三次發射后累積可靠度降低較多，需要進行一次大修提升運載火箭可靠度水平。修復后進行下一輪執行任務的第一次發射任務，依次執行任務到第三輪的最后一次發射前將進行最后一次大修，之后即使進行維修也可能無法達到任務可靠度的要求。

2.1.2 參數設計

通過參考飛機、衛星等的RMT指標參數，設計本文可重復使用運載火箭的RMT指標參數，具體見表1。涉及的基本參數為：可靠性R、維修性M、測試性Te以及可用度A。

表1 可重復運載火箭維修性、可靠性、可用度、可測試性指標參數設計Tab.1 Parameter design of maintainability，reliability，availability and testability of repeatable launch vehicle

2.2 基于期望任務壽命的可重復運載火箭RMT指標的分配

2.2.1 以第二次發射前可用度為基準反推第一次發射過程的可靠性、失效率指標

以第二次發射前可用度為基準反推第一次發射過程的可靠性、失效率指標思路，如圖9所示。

圖9 以第二次發射前可用度為基準反推第一次發射過程可靠性、失效率指標思路示意圖Fig.9 Schematic diagram of the idea of calculating the reliability and failure rate index of the first launch process based on the availability before the second launch

(1)第一次發射過程失效率推算

首先給定第二次發射前的可靠度R2.0=0.98，可理解為：由第一次發射、回收、測試、維修后求得的穩態解A1.0得到，其中穩態解是由第一次發射過程的失效率與回收后的維修率求得，即

(21)

其中，μ1.0小綜為第一次發射后小修的維修率，根據式(11)中結果μ1.0小綜=0.807，又已知R2.0=0.98，所以第一次發射過程的失效率為

(22)

(2)第一次發射前可靠度推算

已知任務時間為200 s，將其作為第一次發射過程的1個有效單位時間，根據第一次發射過程的失效率與其第一次發射前可靠度關系R1.0=e-λ1.0t1.0，以及式(22)得到的第一次發射過程的失效率λ1.0=0.017，可以得到第一次發射前的可靠度為

R1.0=e-λ1.0t1.0=e-0.017=0.984

(23)

(3)第一次發射后可靠度推算

第一次發射后的可靠度是由第一次發射前的可靠度與失效率的馬爾可夫狀態轉移矩陣求得，過程如下：

假設：Q1.0表示第一次發射前的可靠性狀態，

Q1.0=

(24)

其中，R1.0為第一次發射前的可靠度，根據式(23)得R1.0=0.984。

P1.0表示第一次發射任務過程的馬爾可夫狀態轉移矩陣，在該矩陣中，狀態2為吸收狀態，狀態轉移到2狀態(待維修狀態)后，將不再轉移到1狀態(正常工作狀態)，所以此時維修部分應取維修率為0，見圖10。

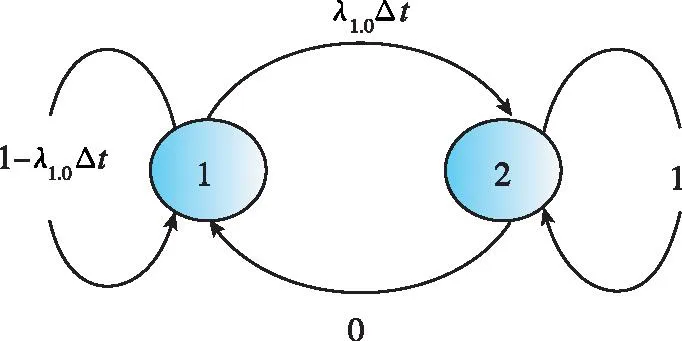
圖10 第一次發射過程(維修前)的馬爾可夫狀態轉移過程Fig.10 Markov state transition during the first launch (before maintenance)

(25)

第一次發射過程的一次可靠性狀態轉移矩陣為

PR1.1=Q1.0P1.0

(26)

其中，R1.1為第一次發射完成后，且維修之前的可靠度；PR1.1是第一次發射過程的一次可靠性狀態轉移矩陣。根據矩陣的運算可得

PR1.1=

(27)

其中，R1.0為第一次發射前的可靠度，根據式(23)得R1.0=0.984。λ1為第一次發射過程的失效率，根據式(22)得λ1.0=0.017。Δt為1個有效單位時間，所以有

(28)

此時，第一次發射后的可靠性為

R1.1=R1.0(1-λ1.0Δt)=0.967

(29)

(4)第一次發射完成，維修前可靠度下降程度

經過第一次發射后，可靠度下降了(已知R1.0=0.984，R1.1=0.967)

ΔR1=R1.0-R1.1=0.984-0.967=0.017

(30)

2.2.2 基于馬爾可夫過程的可重復運載火箭第二次發射過程解析

(1)第二次發射過程失效率的計算

第二次發射前的任務可靠度為R2.0=0.98。

假設：Q2.0表示第二次發射前的可靠性狀態，

Q2.0=

(31)

根據可靠度的計算公式

R2.0=e-λ2.0t2.0

(32)

當t2.0為第二次發射過程的1個有效單位時間時

(33)

與第一次發射的失效率λ1.0=0.017比，第二次發射的失效率λ2.0比λ1.0高了

Δλ1=λ2.0-λ1.0=0.02-0.017=0.003

(34)

(2)第二次發射過程可靠性狀態馬爾可夫穩態分析(不考慮維修)

第二次發射任務過程的狀態轉移矩陣P2.0，其中2狀態為吸收狀態，如圖11所示。

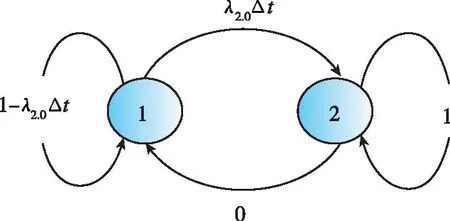
圖11 第二次發射過程(維修前)的馬爾可夫狀態轉移過程Fig.11 Markov state transition during the second launch (before maintenance)

(35)

(3)第二次發射過程可靠性狀態轉移求解

第二次發射過程的一次可靠性狀態轉移矩陣PR2.1為

PR2.1=Q2.0P2.0

(36)

其中，R2.1為第二次發射完成后，且維修之前的可靠度；PR2.1是第二次發射過程的一次可靠性狀態轉移矩陣。根據矩陣的運算可得

PR2.1=

(37)

其中，R2.0為第二次發射前的可靠度，已知R2.0=0.98。λ2.0為第二次發射過程的失效率，根據公式(33)得λ2.0=0.02。Δt為1個有效單位時間，所以有

(38)

此時，第二次發射后的可靠性為

R2.1=R2.0(1-λ2.0Δt)=0.96

(39)

(4)第二次發射過程可靠性降低程度

經過第二次發射后，的可靠度下降了(已知R2.0=0.98，R2.1=0.96)

ΔR2=R2.0-R2.1=0.98-0.96=0.02

(40)

(5)第二次發射后，考慮維修的穩態可用度求解

第二次發射狀態轉移圖如圖12所示。

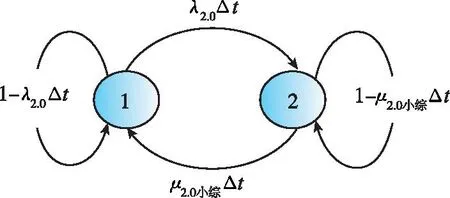
圖12 第二次發射過程(考慮綜合維修情況)的馬爾可夫狀態轉移過程Fig.12 Markov state transition process of the second launch process (considering comprehensive maintenance)

該圖表示發射過程包括發射、維修兩種狀態，所以由狀態轉移圖得狀態轉移矩陣

(41)

由式(7)可知小修維修率μ2.0小綜=0.807，由式(33)得到的第二次發射過程失效率λ2.0=0.02時，則穩態時的可用度狀態矩陣A2.0為

(42)

與第一次發射后回收并小修后的可用度A1.0(第二次發射前可靠度)相比，第二次發射后回收并小修后的可用度A2.0比A1.0=R2.0=0.98低

ΔA1=A1.0-A2.0

=0.98-0.976=0.004

(43)

注：第二次發射前的可靠度R2.0=0.98，可理解為：由第一次發射、回收、測試、維修后求得的穩態解A1.0，兩者值相等，其中穩態解是可通過第一次發射過程的失效率與回收后的維修率求得。

2.2.3 基于馬爾可夫過程的可重復運載火箭第三次發射過程解析

(1)第三次發射過程失效率的計算

第三次發射前的任務可靠度是由第二次發射后回收并小修的可用度A2.0得到，即

R3.0=A2.0=0.976

(44)

其中，Q3.0表示第三次發射前的可靠性狀態

(45)

根據可靠度的計算公式

R3.0=e-λ3.0t3.0

(46)

當t3.0為第二次發射過程1個有效單位時間時

(47)

與第二次發射的失效率λ2.0=0.02比，第三次發射的失效率λ3.0比λ2.0高了

Δλ2=λ3.0-λ2.0=0.025-0.02=0.005

(48)

(2)第三次發射過程可靠性狀態馬爾可夫穩態分析(不考慮維修)

第三次發射任務過程的狀態轉移矩陣P3.0，其中2狀態為吸收狀態，如圖13所示。

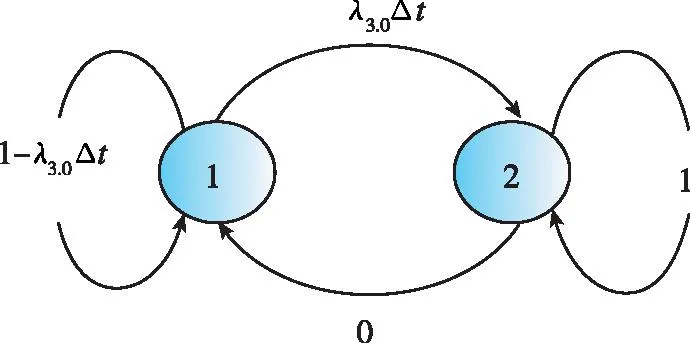
圖13 第三次發射過程(維修前)的馬爾可夫狀態轉移過程Fig.13 Markov state transition process during the third launch (before maintenance)

(49)

(3)第三次發射過程可靠性狀態轉移求解

第三次發射過程的一次可靠性狀態轉移矩陣PR3.1為

PR3.1=Q3.0P3.0

(50)

其中，R3.1為第三次發射完成后，且維修之前的可靠度；PR3.1是第三次發射過程的一次可靠性狀態轉移矩陣。根據矩陣的運算可得

PR3.1=

(51)

其中，R3.0為第三次發射前的可靠度，已知R3.0=0.976。λ3.0為第三次發射過程的失效率，根據式(47)得λ3.0=0.025。Δt為1個有效單位時間，所以有

(52)

此時，第三次發射后的可靠性為

R3.1=R3.0(1-λ3.0Δt)=0.951

(53)

(4)第三次發射過程可靠性降低程度

此時經過第三次發射后的可靠度下降了(已知R3.0=0.976，R3.1=0.951)

ΔR3=R3.0-R3.1

=0.976-0.951=0.025

(54)

(5)第三次發射后，考慮維修的穩態可用度求解

第三次發射狀態轉移圖如圖14所示。

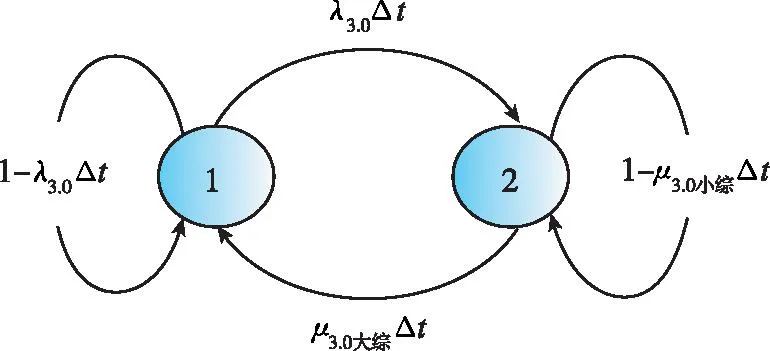
圖14 第三次發射過程(考慮綜合維修情況)的馬爾可夫狀態轉移過程Fig.14 Markov state transition process of the third launch process (considering comprehensive maintenance)

圖14表示發射過程包括發射、維修兩種狀態，所以由狀態轉移圖得狀態轉移矩陣

(55)

由式(7)可知大修維修率μ3.0大綜=0.979，以及式(47)得到的第三次發射過程失效率λ3.0=0.025，則穩態時的可用度狀態A3.0為

(56)

與第二次發射后回收并小修后的可用度A2.0=R3.0=0.976(第三次發射前可靠度)相比，第三次發射后回收并大修后的可用度A3.0比A2.0低

ΔA2=A2.0-A3.0

=0.976-0.975=0.001

(57)

2.2.4 基于期望壽命周期的可重復運載火箭RMT指標的計算分析

根據如上過程，總任務期望發射次數為10次，其中3次發射為一個任務輪次，每個任務輪次的維修水平分別設為小修、小修、大修，其中第二個任務輪次與第一次任務輪次計算過程相同，則結果如表2所示。

表2 基于期望壽命周期的可重復運載火箭RMT指標的數據分析表Tab.2 Data analysis table of RMT index of repeatable launch vehicle based on expected life cycle

3 結束語

本文綜合運用了可靠性工程理論、可用度、馬爾柯夫狀態轉移過程理論等等，設計了基于RMT的可重復運載火箭的穩態可用度解析模型，對可重復運載火箭的發射過程進行了解析。明確可重復運載火箭發射過程中的可靠性、維修性等參數，針對復雜裝備的指標要求進行研究，建立了基于期望任務壽命的可重復運載火箭RMT指標參數規劃模型，供可重復運載火箭參考。