多階段屈服U形金屬阻尼器抗震性能研究
王德斌,王英豪,趙漢濤
(1.大連交通大學 土木工程學院,遼寧 大連 116028; 2.中建一局集團建設發展有限公司,北京 100102)
現有消能減震結構往往通過附加耗能構件耗散地震輸入的大部分能量,該方法能夠有效降低主體結構的地震響應和損傷。金屬阻尼器以其力學模型簡單、滯回性能穩定、抗疲勞性能良好、制造安裝方便等優勢,在實際工程中得到廣泛應用和推廣[1]。
金屬阻尼器能夠為結構提供附加剛度和阻尼,有效降低結構在地震荷載作用下的位移響應。Zibasokhan等[2]提出了一種純彎曲變形金屬阻尼器,該阻尼器具有穩定的滯回、變形性能,耗能能力優異。Deng等[3]提出了設置加勁板的剪切型金屬阻尼器,該阻尼器能夠在低位移水平下實現剪切耗能,加勁板的設置提升了阻尼器的防屈曲能力,耗能能力得到顯著提高。王德斌等[4]基于扭轉變形機制提出了一種具有多截面屈服,應力、應變分布均勻的新型扭轉鋼管阻尼器,將其應用于支撐鋼框架,展示了較好的減震控制效果。程揚等[5]將矩形剪切鋼板與U形鋼板進行并聯組合,提出了一種具有多階段屈服特點的金屬阻尼器,該阻尼器能夠在不同強度的地震作用下實現分階段屈服的耗能目標。吳山等[6]采用不同尺寸的鋼條作為耗能構件,提出了具有多階段屈服和失效特性的金屬套管阻尼器。
目前金屬阻尼器在研究和應用中仍存在以下問題:①現有金屬阻尼器往往針對中大震進行性能設計,難以在低位移水平下的彈性狀態實現耗能[7-8];②部分剪切型金屬阻尼器雖能在低位移水平下實現屈服耗能,高位移水平下則強度退化明顯,難以達到結構更高的耗能需求;③單一破壞階段的金屬阻尼器,耗能組件發生破壞后,阻尼器迅速失效,無法滿足后續地震作用下結構的耗能需求[9]。
基于上述分析,本文提出了一種具有多階段屈服和失效特點的U形金屬阻尼器。給出了該阻尼器的基本構造、工作機理和恢復力模型,采用Abaqus軟件對其滯回性能、耗能能力和破壞過程進行了分析,通過對比有限元模擬結果和恢復力模型,驗證了恢復力模型的準確性。
1 阻尼器基本構造和理論模型
1.1 基本構造和工作機理
本文設計的多階段屈服U形金屬阻尼器構造見圖1。該阻尼器由具有不同尺寸參數的上下和前后對稱布置的U形耗能鋼板及內部加載軸桿、外部約束套筒所組成,U形鋼板中部截取部分平直段長度,采用焊接的形式固結于約束套筒和加載軸桿之上。U形鋼板在外荷載作用下發生滾動彎曲變形并進行屈服耗能,其屈服截面隨位移的變化不斷移動,形成多截面屈服的變形特點,能夠有效提升耗能鋼板的抗疲勞性能。

(a) 阻尼器整體構造
阻尼器尺寸參數見圖2。通過調整阻尼器U形鋼板A、B的尺寸,實現低位移水平下U形鋼板A率先發生屈服,此時阻尼器的受力和耗能主要由U形鋼板A承擔。在高位移水平下U形鋼板A發生破壞,承載能力和耗能能力下降,此時U形鋼板B發生屈服,并充分發揮其變形能力強、抗疲勞性能好的優勢,完成后續承載工作。

(a) 側視圖
本文共設計3種阻尼器工況,試件1僅對稱布置U形鋼板A,試件2僅對稱布置U形鋼板B,試件3則由試件1和2組合,前后和上下分別對稱布置U形鋼板A和B,進而實現多階段屈服耗能,各工況下試件的具體尺寸參數見表1。

表1 阻尼器U形鋼板尺寸參數 mm
1.2 恢復力模型
阻尼器的屈服荷載、初始剛度、屈服后剛度和極限荷載作為阻尼器的重要力學性能指標,對其理論恢復力模型的建立極其重要。本文單個雙U形阻尼器的全截面屈服荷載Fy、初始剛度K1和屈服后剛度K2、等效屈服位移δy、極限荷載Fu表達式[10]為:
(1)
(2)
K2=αK1
(3)
(4)
Fu=βFy
(5)
式中:ω為U形鋼板寬度;σy為U形鋼板材料屈服強度;t為U形鋼板厚度;d為U形鋼板圓弧段內側直徑;μ為初始剛度修正系數;E為材料彈性模量;α為雙U形鋼板屈服后剛度與初始剛度之比;β為雙U形鋼板極限荷載與屈服荷載之比。
以阻尼器受拉時的荷載-位移曲線和剛度變化為例,其在不同加載階段的力學模型見圖3。阻尼器各加載階段下兩組U形鋼板的變形相同,U形鋼板A和U形鋼板B屬并聯關系, 其力學模型是由兩者力學性能指標的線性疊加所組成。阻尼器剛度的變化主要經歷三個不同的受力階段。
OA段,阻尼器開始加載至U形鋼板A屈服前,此時0<δ≤δy1。U形鋼板B并未發生屈服,其剛度和承載力計算表達式為:
δy1=δyA,K1=2(K1A+K1B),F=K1δ
(6)
Fy1=FyA+K1BδyA
(7)
AB段,阻尼器U形鋼板A屈服后至U形鋼板B屈服前,此時δy1<δ≤δy2。阻尼器剛度和承載力計算表達式為:
δy2=δyB,K2=2(K2A+K1B),F=K2δ
(8)
Fy2=Fy1+K2(δyB-δyA)
(9)
BC段,阻尼器U形鋼板B屈服后直至加載至最大荷載Fmax之前,此時δy2<δ≤δmax。阻尼器剛度和承載力計算表達式為:
K3=2(K2A+K2B),F=K3δ
(10)
2 阻尼器有限元模型
本文基于Abaqus軟件建立阻尼器有限元模型,約束套筒在不影響阻尼器力學性能的情況下采用一體式建模,阻尼器各部件均采用八節點線性六面體減縮積分實體單元(C3D8R),U形鋼板A和B與加載軸桿、約束套筒均采用Tie綁定連接,加載軸桿受力端建立參考點RF并與其端部進行剛體耦合,位移荷載施加于參考點RF之上,初始加載幅值為5 mm,并以5 mm作為位移增量,直至加載至40 mm完成加載,各級幅值均往復循環加載兩周。約束套筒、加載軸桿單元尺寸為20 mm,U形鋼板單元尺寸細化取5 mm。阻尼器有限元模型見圖4。

圖4 阻尼器有限元模型
阻尼器有限元模型中,加載軸桿、外部約束套筒采用Q345鋼,整個加載過程中始終處于線彈性狀態。U形耗能鋼板采用Q235級鋼,屈服強度σy為235 MPa,彈性模量E為206 GPa,泊松比ν為0.3,采用隨動強化本構模型,強化階段彈性模量為0.01E。
3 模擬結果分析
3.1 滯回性能
各工況下阻尼器滯回曲線見圖5,各試件滯回曲線飽滿、穩定。從圖5可以看出,試件1和2的屈服位移和極限位移均存在一定差異,試件1屈服位移較低,隨著位移的增大其變形已由滾動彎曲屈服轉換為拉伸變形, 承載力顯著提高, 即將發生拉伸破壞,限于軟件中材料難以反映阻尼器下降段特征,依據其變形發展趨勢可判定試件1總體變形破壞過程。而試件2不論在高位移還是低位移下均展現出了穩定的變形性能,并未出現明顯的承載力提升現象,仍處于滾動彎曲屈服狀態,高位移水平下展現出穩定的變形能力和耗能能力。
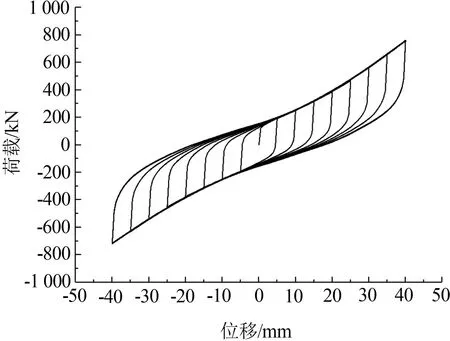
(a) 試件1
試件3滯回曲線則結合試件1和2兩者的力學性能差異,承載力值為試件1和2之和,其能夠實現低位移水平下的屈服耗能,又能確保高位移水平下具有一定的變形和耗能能力,滿足結構的大變形需求。同時從曲線可以看出,在加載后期阻尼器承載力顯著提升,可見該阻尼器不僅能夠滿足高位移水平下的耗能需求,又能依靠基于彎曲變形向拉伸變形轉換的U形耗能鋼板滿足大震下結構更高的承載力需求。
3.2 耗能性能
等效黏滯阻尼比是構件耗能能力的重要評價指標,圖6給出了不同工況下試件的等效阻尼比隨位移幅值的變化曲線。可以看出,各試件的等效黏滯阻尼比在加載初期迅速增大,加載后期則展現出不同的變化特征。試件1在加載后期等效黏滯阻尼比迅速下降,耗能能力明顯降低,其原因主要是隨著變形的增大U形鋼板變形由彎曲向拉伸轉換進而受拉破壞,耗能能力顯著降低。而試件2具有較強的變形能力,在加載后期并未發生明顯破壞,其等效黏滯阻尼比下降速度平穩,仍能有效吸收外部能量。試件3的等效黏滯阻尼比變化特征介于試件1和2之間,同時具備兩者的變形、耗能優勢,既能在低位移水平下完成高耗能,又能確保在大位移下仍具備良好的耗能能力。

圖6 不同工況下試件的等效阻尼比隨位移幅值的變化曲線
3.3 破壞過程
圖7給出了試件3在位移幅值下U形鋼板的等效塑性應變云圖。可以看出,塑性應變主要發生在U形鋼板平直段和圓弧過渡段。在加載至δ=5 mm幅值時,U形鋼板A已展現出顯著的塑性變形,而U形鋼板B屈服區域極其有限,等效塑性應變值較低。隨著位移幅值的進一步增大,U形鋼板A的屈服區域明顯向弧形板一側延伸,塑性變形區域明顯增加,多個截面均處于高塑性變形區,此時U形鋼板B塑性變形區域同樣進一步擴展。在δ=20 mm時,U形鋼板A已出現由彎曲屈服向受拉變形轉換,形成整截面屈服的變化趨勢,而U形鋼板B仍具有顯著變形能力,其U形板上下表面并未發生屈服,可見其能夠滿足結構的大變形需求,進而使阻尼器能夠實現多階段屈服耗能。

(a) δ=5 mm
4 恢復力模型驗證
圖8給出了試件3數值模擬和理論力學模型的荷載-位移滯回曲線和骨架曲線的對比結果。可以看出,理論力學模型給出的三折線模型與數值模擬得到的荷載-位移滯回曲線基本吻合,驗證了理論力學模型的準確性。阻尼器設計過程中,可以針對不同結構的抗震設計需求,依據本文給出的不同加載階段的直線表達式實現不同地震強度下阻尼器的承載力、剛度和變形設計要求。

圖8 阻尼器模擬和理論模型結果對比
5 結論
本文基于U形鋼板的力學性能特點提出了一種多階段屈服金屬阻尼器,給出了其三折線力學模型,通過數值模擬研究了阻尼器的主要力學性能,得到以下結論:
(1)該多階段屈服金屬阻尼器由2種不同尺寸參數的雙U形鋼板并聯而成,能夠在不同強度下進行分階段屈服耗能,實現多級設防水準下的結構抗震理念;阻尼器滯回曲線飽滿,具有良好的耗能能力。
(2)低位移水平下高承載力U形鋼板率先發生屈服并進行耗能,其塑性變形區域擴展迅速,高位移水平下其變形機制由彎曲轉變為拉伸并發生破壞,此時低承載力U形鋼板作為主要耗能部件進行耗能。
(3)兩類U形鋼板在低位移水平下等效黏滯阻尼比均迅速增大,隨著位移的增大低承載力U形鋼板等效黏滯阻尼比迅速減小,耗能能力降低,而高承載力U形鋼板的等效黏滯阻尼比平穩下降,具有更加穩定的耗能能力。
(4)基于Abaqus軟件建立了阻尼器有限元模型,模擬得到滯回曲線與給出的分階段三折線力學模型基本吻合,該力學模型能夠很好地反映阻尼器的主要性能指標,可依據結構的不同強度設計要求完成阻尼器的尺寸參數設計。

