基于足間距信息輔助的行人三維慣性定位算法

路永樂,蘇 勝,楊 杰,羅 毅,粟 萍,惠嘉威

(重慶郵電大學(xué)智能傳感技術(shù)與微系統(tǒng)重慶市高校工程研究中心,重慶 400065)

0 引言

導(dǎo)航系統(tǒng)指為行人提供位置信息服務(wù)的系統(tǒng),通常利用衛(wèi)星定位系統(tǒng)實(shí)現(xiàn)室外導(dǎo)航定位[1],但人類大部分的活動(dòng)都發(fā)生在室內(nèi)環(huán)境中,衛(wèi)星信號(hào)會(huì)受建筑物墻壁遮擋,導(dǎo)致信號(hào)衰弱嚴(yán)重,進(jìn)而無法提供可靠的室內(nèi)導(dǎo)航服務(wù)[2]。而慣性導(dǎo)航系統(tǒng)(inertial navigation system, INS)以慣性測(cè)量單元(inertial measurement unit, IMU)提供的加速度和角速度信息為基礎(chǔ),利用捷聯(lián)慣導(dǎo)算法解算得到位姿信息,實(shí)現(xiàn)導(dǎo)航定位[3]。由于INS不需要外界信息輔助,具有自主性強(qiáng)、抗干擾能力強(qiáng)等優(yōu)勢(shì),在單兵作戰(zhàn)、火場(chǎng)救援及室內(nèi)導(dǎo)航等領(lǐng)域成為了主要研究方向[4-5]。

但是IMU存在不可避免的誤差,導(dǎo)致INS定位結(jié)果出現(xiàn)嚴(yán)重漂移,無法提供準(zhǔn)確的定位服務(wù)[6]。為抑制行人INS累積誤差,Foxlin等[7]采用零速修正(zero velocity update, ZUPT)算法,在靜止區(qū)間內(nèi)利用零速條件修正系統(tǒng)誤差。但ZUPT算法無法解決航向角誤差漂移的問題,長航時(shí)定位結(jié)果仍會(huì)偏離真實(shí)情況[8]。

基于以上問題,研究人員對(duì)行人INS誤差修正進(jìn)行了以下三方面的研究:1)利用多傳感器融合抑制航向漂移。孫猛等[9]利用磁力計(jì)測(cè)量磁場(chǎng)信息,并利用擴(kuò)展卡爾曼濾波構(gòu)建基于磁定位和行人航跡推算(pedestrian dead reckoning,PDR)的融合系統(tǒng),實(shí)現(xiàn)室內(nèi)定位;何成陽等[10]利用超寬帶(ultra wide band,UWB)無線通信技術(shù)輔助IMU定位,并利用聯(lián)邦導(dǎo)數(shù)容積卡爾曼濾波器對(duì)航向誤差進(jìn)行修正。2)部署多IMU約束誤差。李興等[11]利用IMU陣列實(shí)現(xiàn)位置解算,并根據(jù)漂移誤差情況自適應(yīng)融合陣列數(shù)據(jù),提高行人導(dǎo)航精度;李曉東等[12]在行人雙腿關(guān)節(jié)處部署6個(gè)IMU,利用人體關(guān)節(jié)信息構(gòu)建雙足約束模型來抑制航向誤差。3)利用外界信息實(shí)現(xiàn)高度解算。陸傳華等[13]利用氣壓計(jì)更新高度信息,并利用地圖信息限制高度更新的區(qū)域,最終實(shí)現(xiàn)行人高度解算;俞敏杰等[14]在大樓內(nèi)部署信號(hào)源,根據(jù)接收來自各樓層信號(hào)強(qiáng)度差值的分布情況,確定行人所在樓層。

上述方法可以有效修正系統(tǒng)誤差,但引入其他傳感器增加了系統(tǒng)的復(fù)雜性和成本,并且導(dǎo)航系統(tǒng)只能在特定場(chǎng)景內(nèi)工作,不具有普遍適用性。基于以上問題,本文提出了一種基于足間距離信息輔助的行人慣性定位算法。該算法利用隨機(jī)森林算法對(duì)行人的動(dòng)作模式進(jìn)行識(shí)別,并采用基于時(shí)間因子修正的自適應(yīng)零速檢測(cè)算法,實(shí)現(xiàn)了對(duì)零速區(qū)間的高精度劃分;在平面運(yùn)動(dòng)中,通過利用超聲測(cè)距的足間距約束模型修正導(dǎo)航誤差,有效限制了航向誤差的發(fā)散;而在樓梯運(yùn)動(dòng)情況下,采用基于臺(tái)階高度和足間距信息的高度解算算法,實(shí)現(xiàn)了對(duì)高度信息的準(zhǔn)確解算,有效避免了高度的發(fā)散。在保證系統(tǒng)自主性、便攜性和普遍適用性的同時(shí),可以有效提高雙足IMU導(dǎo)航系統(tǒng)的定位精度。

1 基于足間距信息的位置解算

1.1 基于超聲測(cè)距的足間距約束模型

INS根據(jù)IMU采集的行人運(yùn)動(dòng)數(shù)據(jù),建立“東北天”導(dǎo)航坐標(biāo)系(n系)和“右前上”載體坐標(biāo)系(b系),利用捷聯(lián)慣導(dǎo)解算獲得行人導(dǎo)航信息,導(dǎo)航信息解算方程如下[15]

(1)

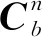
將根據(jù)式(1)得到的任意時(shí)刻行人左右腳導(dǎo)航狀態(tài)表示為

(2)

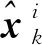
(3)

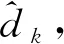
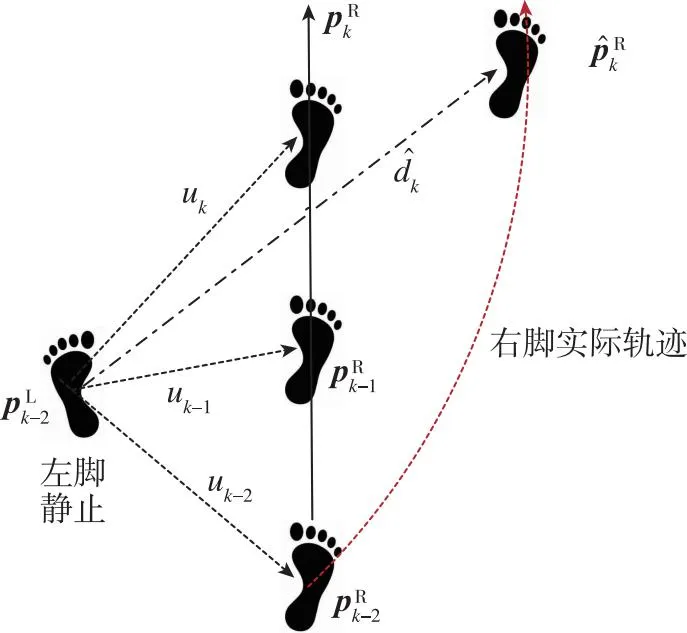
圖1 行人單次邁步足部示意圖

(4)

(5)

(6)

(7)

當(dāng)任意時(shí)刻左右腳位置關(guān)系不滿足足間距約束模型時(shí),利用式(7)可以得到雙足位置誤差為

(8)

考慮到行人運(yùn)動(dòng)的每個(gè)步態(tài)周期中都存在一只靜止腳與一只擺動(dòng)腳,利用零速修正算法修正靜止腳所處的導(dǎo)航子系統(tǒng),并將靜止腳作為參考基準(zhǔn),利用足間距約束模型對(duì)擺動(dòng)腳所處的導(dǎo)航子系統(tǒng)進(jìn)行修正。在行人行走過程中雙足交替進(jìn)行擺動(dòng),雙足IMU導(dǎo)航系統(tǒng)將不斷地對(duì)行人雙腳導(dǎo)航子系統(tǒng)交替進(jìn)行零速修正和足間距約束修正,最終提高雙足IMU導(dǎo)航系統(tǒng)的定位精度。基于卡爾曼濾波的雙足導(dǎo)航子系統(tǒng)的誤差修正模型如下

(9)

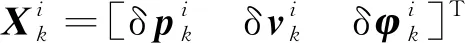
(10)

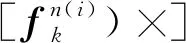
(11)

其中,an表示n系下的加速度。

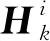
(12)

(13)

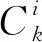
1.2 基于臺(tái)階高度與足間距的高度解算算法

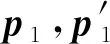
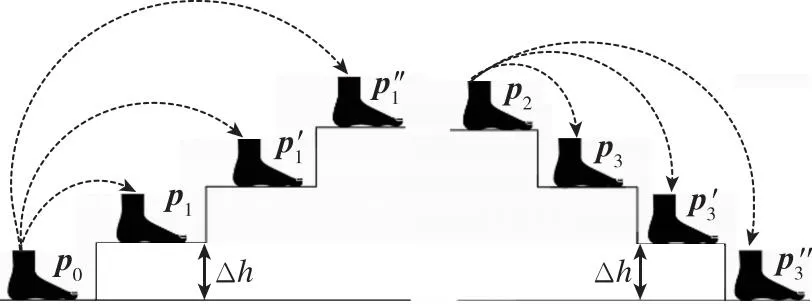
圖2 行人上下樓梯運(yùn)動(dòng)示意圖

在已知臺(tái)階高度信息的情況下,利用單次邁步中初始位置與終點(diǎn)位置間的足間距信息,求取單次邁步跨越臺(tái)階數(shù),便可以實(shí)現(xiàn)行人的高度解算。設(shè)單次邁步的起點(diǎn)和終點(diǎn)平面位置坐標(biāo)分別如式(14)所示

(14)

由行人單次邁步的前后零速區(qū)間平面位置,可以計(jì)算出單次邁步跨越臺(tái)階數(shù)為

(15)

其中,N為單次邁步跨越臺(tái)階數(shù);thstair為跨越臺(tái)階數(shù)判斷閾值;floor(·)為向下取整函數(shù)。當(dāng)行人處于上樓運(yùn)動(dòng)時(shí),N值為式(16)計(jì)算值;當(dāng)行人處于下樓運(yùn)動(dòng)時(shí),N值為式(16)計(jì)算值的相反數(shù),具體表達(dá)式為

(16)

利用單次邁步跨越臺(tái)階數(shù)、臺(tái)階高度信息以及邁步總數(shù)便可以得到行人的高度信息

(17)

其中,hk為行人當(dāng)前高度信息;i為邁步序號(hào);n為總邁步數(shù);Ni為第i次邁步跨越的臺(tái)階數(shù)。

2 足間距輔助IMU行人定位系統(tǒng)

2.1 總體框架

本研究在行人雙腳腳跟位置安裝IMU與超聲測(cè)距模塊,采集行人運(yùn)動(dòng)數(shù)據(jù),利用捷聯(lián)慣導(dǎo)算法解算行人導(dǎo)航信息。由于行人在建筑物內(nèi)存在平面運(yùn)動(dòng)與上下樓運(yùn)動(dòng),因此首先利用隨機(jī)森林算法對(duì)行人運(yùn)動(dòng)模式進(jìn)行識(shí)別,當(dāng)行人處于平面運(yùn)動(dòng)時(shí),根據(jù)超聲測(cè)距模塊測(cè)得的雙足相對(duì)距離信息,建立足間距約束模型,并結(jié)合零速修正算法,利用卡爾曼濾波修正雙足導(dǎo)航誤差;當(dāng)行人處于上下樓運(yùn)動(dòng)時(shí),利用臺(tái)階高度信息進(jìn)行高度解算,最終實(shí)現(xiàn)三維導(dǎo)航定位。超聲測(cè)距輔助雙足IMU行人定位系統(tǒng)的總體框架如圖3所示,其中γ為零速修正閾值,ΔT為時(shí)間因子。

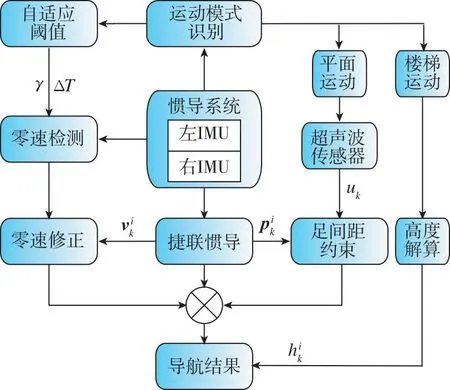
圖3 總體框架

2.2 零速檢測(cè)

如圖4所示,行人行走過程中足部特征由運(yùn)動(dòng)區(qū)間和靜止區(qū)間交替構(gòu)成,在靜止區(qū)間中,足部完全接觸地面,此時(shí)足部理論速度為零,直到再次進(jìn)入運(yùn)動(dòng)區(qū)間[16]。

圖4 足部運(yùn)動(dòng)特征

零速修正算法將靜止時(shí)捷聯(lián)慣導(dǎo)解算速度作為誤差觀測(cè)量,利用卡爾曼濾波修正導(dǎo)航誤差[17]。而使用零速修正算法的前提是正確地劃分足部運(yùn)動(dòng)狀態(tài),本文采用廣義似然比檢測(cè)法(generalized likelihood ratio test, GLRT)對(duì)足部運(yùn)動(dòng)狀態(tài)進(jìn)行劃分[18]

(18)

(19)

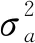
本文提出基于時(shí)間因子修正的零速檢測(cè)算法,用來消除初步劃分中的誤判情況。具體步驟為:

1)根據(jù)運(yùn)動(dòng)模式選擇γ閾值和時(shí)間因子ΔT,利用GLRT零速檢測(cè)算法對(duì)行人足部狀態(tài)進(jìn)行初步劃分。將運(yùn)動(dòng)區(qū)間和靜止區(qū)間分別定義為Cmove,i和Cstatic,i,其中Cmove,i表示第i個(gè)運(yùn)動(dòng)區(qū)間內(nèi)包含的數(shù)據(jù)數(shù)量,Cstatic,i表示第i個(gè)靜止區(qū)間內(nèi)包含的數(shù)據(jù)數(shù)量。

2)將各區(qū)間的數(shù)據(jù)數(shù)量與時(shí)間因子ΔT進(jìn)行比較。若區(qū)間的數(shù)據(jù)數(shù)量均大于時(shí)間因子,則表示區(qū)間劃分正確,反之,若某一區(qū)間的數(shù)據(jù)數(shù)量小于時(shí)間因子,則表明該區(qū)間劃分錯(cuò)誤。

3)劃分錯(cuò)誤區(qū)間進(jìn)行狀態(tài)翻轉(zhuǎn),即將偽靜止區(qū)間轉(zhuǎn)換為運(yùn)動(dòng)區(qū)間,偽運(yùn)動(dòng)區(qū)間轉(zhuǎn)換為靜止區(qū)間。對(duì)行人各步態(tài)區(qū)間狀態(tài)都進(jìn)行時(shí)間因子檢測(cè),減小誤判和漏判出現(xiàn)的次數(shù),提高零速區(qū)間檢測(cè)精度。

2.3 運(yùn)動(dòng)模式識(shí)別

行人在室內(nèi)運(yùn)動(dòng)時(shí),主要運(yùn)動(dòng)模式包括靜止、行走、跑步及上下樓等。為實(shí)現(xiàn)不同運(yùn)動(dòng)場(chǎng)景算法以及零速檢測(cè)閾值的動(dòng)態(tài)調(diào)整,引入隨機(jī)森林算法對(duì)行人運(yùn)動(dòng)模式進(jìn)行識(shí)別。隨機(jī)森林算法是以決策樹為基礎(chǔ)的集成學(xué)習(xí)模型,其原理為利用boots-trap技術(shù)獲得多個(gè)樣本子集,并使用不同樣本子集構(gòu)建決策樹,當(dāng)輸入待分類數(shù)據(jù)時(shí),各決策樹共同投票實(shí)現(xiàn)隨機(jī)森林分類的算法[19]。分類示意圖如圖5所示,圖中數(shù)字為各動(dòng)作模式的類別標(biāo)簽。

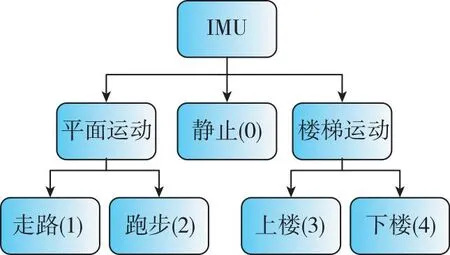
圖5 運(yùn)動(dòng)模式分類示意圖

本文使用的IMU數(shù)據(jù)輸出頻率為200 Hz,采集的原始數(shù)據(jù)表達(dá)式為

(20)

其中,Sorig表示原始運(yùn)動(dòng)數(shù)據(jù);ax,ay,az分別為x軸,y軸,z軸的加速度數(shù)據(jù);ωx,ωy,ωz分別為x軸,y軸,z軸的角速度數(shù)據(jù)。

在采集完測(cè)試人員的運(yùn)動(dòng)數(shù)據(jù)后,采用加窗法對(duì)數(shù)據(jù)進(jìn)行分割,窗口寬度為140,重疊率為50%,并提取三軸加速度和三軸角速度的數(shù)據(jù)特征值,降低識(shí)別和分類的復(fù)雜性,提高效率,由此得到數(shù)據(jù)集D,數(shù)據(jù)集D的表達(dá)式為

D=(F,Y)={(fi,yi)},i=1,2,…,m

(21)

其中,m為樣本個(gè)數(shù);Y表示樣本對(duì)應(yīng)的運(yùn)動(dòng)類型,yi表示樣本i的類型;F表示運(yùn)動(dòng)數(shù)據(jù)的特征矩陣,具體表示為

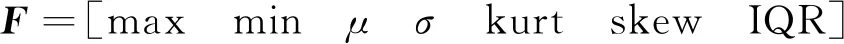
(22)

其中,F為樣本的特征向量,共7組運(yùn)動(dòng)數(shù)據(jù)時(shí)域特征;max,min分別為最大值和最小值;μ,σ分別為均值和方差;kurt,skew分別為峰度和偏度;IQR為四分位距。利用樣本的特征向量對(duì)隨機(jī)森林模型進(jìn)行訓(xùn)練,實(shí)現(xiàn)行人運(yùn)動(dòng)模式分類。

根據(jù)運(yùn)動(dòng)模式分類情況,選取相應(yīng)的算法進(jìn)行導(dǎo)航解算。針對(duì)平面運(yùn)動(dòng),采用1.1節(jié)提出的基于超聲測(cè)距的足間距約束模型,并結(jié)合零速修正算法,抑制INS誤差;針對(duì)上下樓運(yùn)動(dòng),采用1.2節(jié)提出的基于臺(tái)階高度與足間距的高度解算算法,計(jì)算行人高度信息,最終實(shí)現(xiàn)高精度行人三維慣性定位系統(tǒng)。

3 實(shí)驗(yàn)驗(yàn)證

3.1 實(shí)驗(yàn)平臺(tái)搭建

本文選擇大樓室內(nèi)平面和樓梯走道作為算法驗(yàn)證環(huán)境,實(shí)驗(yàn)人員裝備本文搭建的超聲輔助雙足IMU定位系統(tǒng),按照規(guī)劃路線行進(jìn),雙足IMU定位系統(tǒng)示意圖如圖6所示。

圖6 雙足IMU定位系統(tǒng)

系統(tǒng)中IMU為實(shí)驗(yàn)室自研的慣性測(cè)量單元,輸出頻率為200 Hz,主要性能參數(shù)如表1所示;超聲測(cè)距模塊為逐飛科技公司的“有來有去”超聲模塊,對(duì)于短距測(cè)距的誤差情況如表2所示。

表1 IMU主要性能參數(shù)

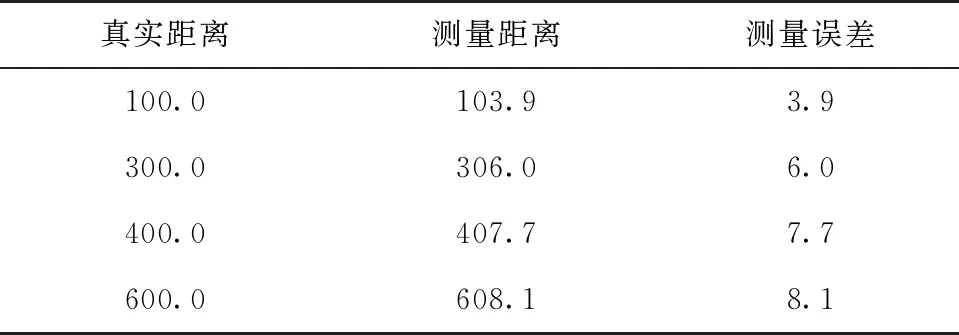
表2 超聲測(cè)距誤差結(jié)果

雙足IMU和超聲測(cè)距傳感器利用AT32F4單片機(jī)實(shí)現(xiàn)數(shù)據(jù)采集與存儲(chǔ)。超聲波測(cè)距模塊進(jìn)行短距測(cè)量時(shí),平均測(cè)量誤差為6.4 mm,測(cè)距精度誤差為2.3%,該誤差能夠滿足本文搭建系統(tǒng)的精度需求。

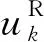
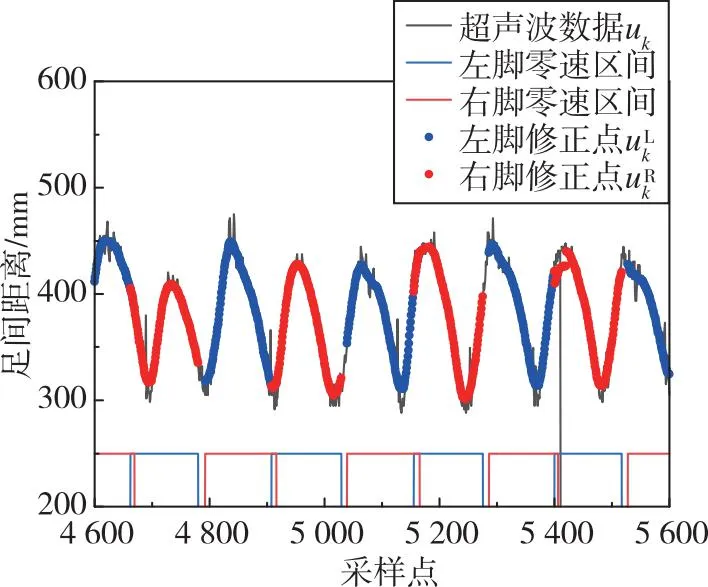
圖7 足間距離測(cè)量結(jié)果

3.2 實(shí)驗(yàn)驗(yàn)證與分析

設(shè)定實(shí)驗(yàn)人員所處的起點(diǎn)坐標(biāo)為(0,0),行走路線的起點(diǎn)與終點(diǎn)坐標(biāo)重合,使用閉環(huán)誤差(起點(diǎn)和終點(diǎn)的歐式距離)和閉環(huán)誤差占比(閉環(huán)誤差占總路程的百分比)作為衡量算法效果的依據(jù),實(shí)驗(yàn)場(chǎng)地如圖8所示。

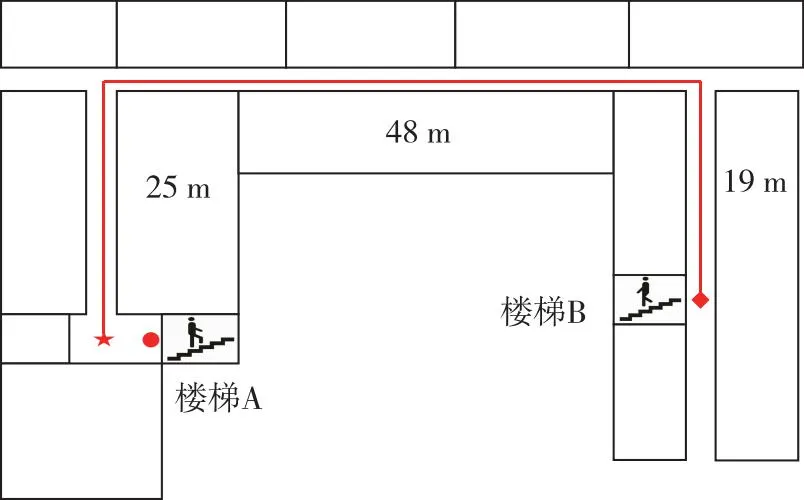
圖8 實(shí)驗(yàn)路線

實(shí)驗(yàn)1:平面閉環(huán)行走實(shí)驗(yàn)。為驗(yàn)證本文超聲波足間距約束算法的有效性,選擇折返路線作為實(shí)驗(yàn)的基準(zhǔn)路線,以星形點(diǎn)作為起點(diǎn),以棱形點(diǎn)為折返點(diǎn),返回起點(diǎn),行進(jìn)距離總計(jì)184.00 m,實(shí)驗(yàn)結(jié)果如圖9所示,軌跡誤差如表3所示。

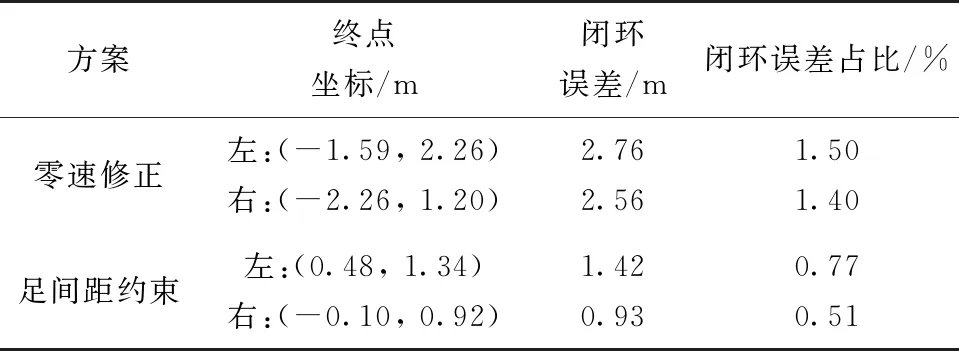
表3 平面定位誤差比較

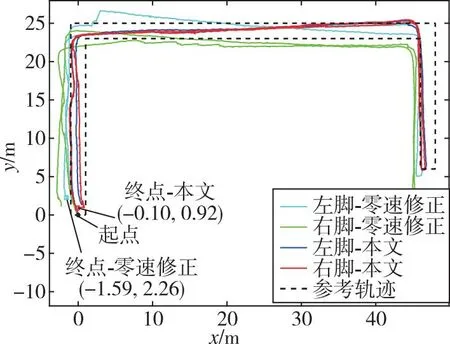
圖9 實(shí)驗(yàn)1運(yùn)動(dòng)軌跡

圖9中淺藍(lán)色線與綠色線為零速修正后的左腳與右腳軌跡,在終點(diǎn)位置雙腳平均閉環(huán)誤差為2.66 m,誤差占比為1.44%。藍(lán)色線與紅色線為經(jīng)本文提出的超聲波足間距約束算法修正后得到的左腳與右腳軌跡,在終點(diǎn)位置雙腳平均閉環(huán)誤差為1.17 m,誤差占比為0.64%,導(dǎo)航誤差與零速修正算法相比下降了55.56%。

實(shí)驗(yàn)2:上下樓實(shí)驗(yàn)。為驗(yàn)證基于臺(tái)階高度與足間距的高度解算算法的有效性,選擇實(shí)驗(yàn)1中的折返路線作為基準(zhǔn)路線,實(shí)驗(yàn)人員以樓梯A圓形點(diǎn)作為起點(diǎn),經(jīng)過樓梯A從二層到達(dá)四層,沿路線到達(dá)樓梯B,經(jīng)過樓梯B從四層達(dá)到二層折返點(diǎn),最后沿路線回到起點(diǎn),該路線二層到四層總高度為7.52 m。高度解算結(jié)果如圖10所示,高度誤差結(jié)果如表4所示,三維軌跡如圖11所示,三維定位誤差如表5所示。

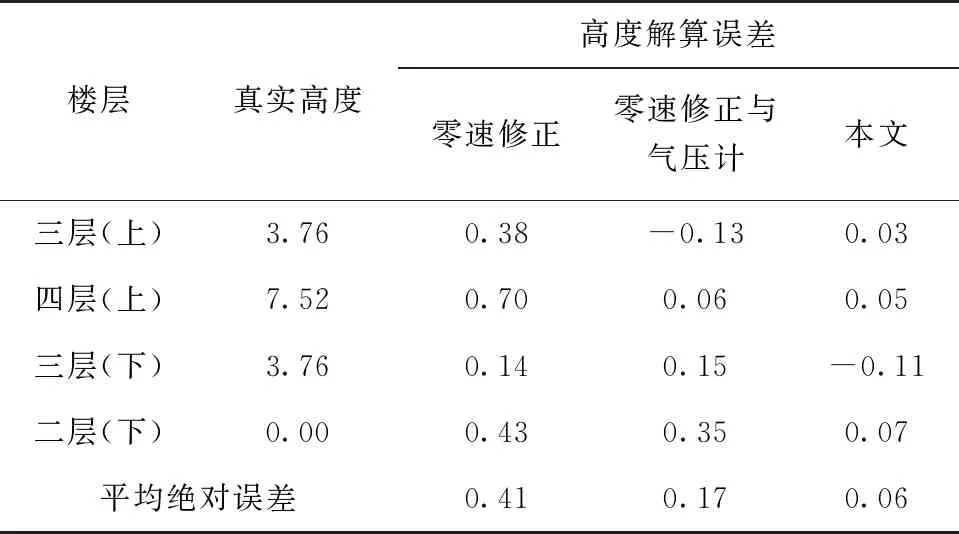
表4 高度解算誤差比較

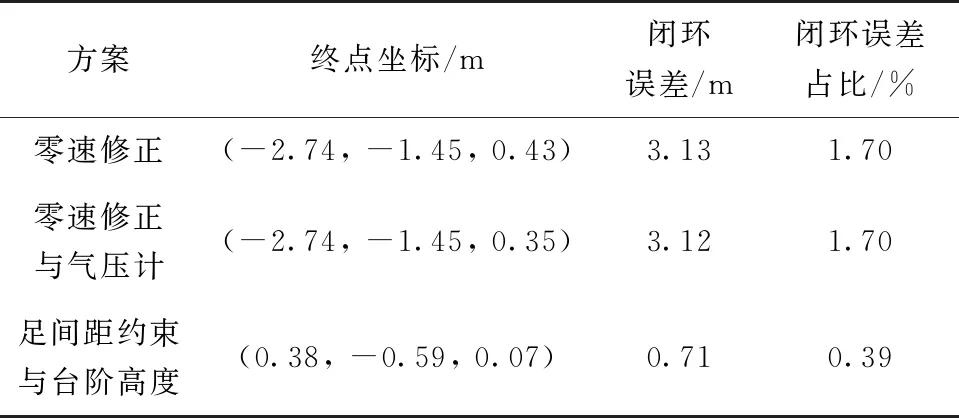
表5 三維定位誤差比較

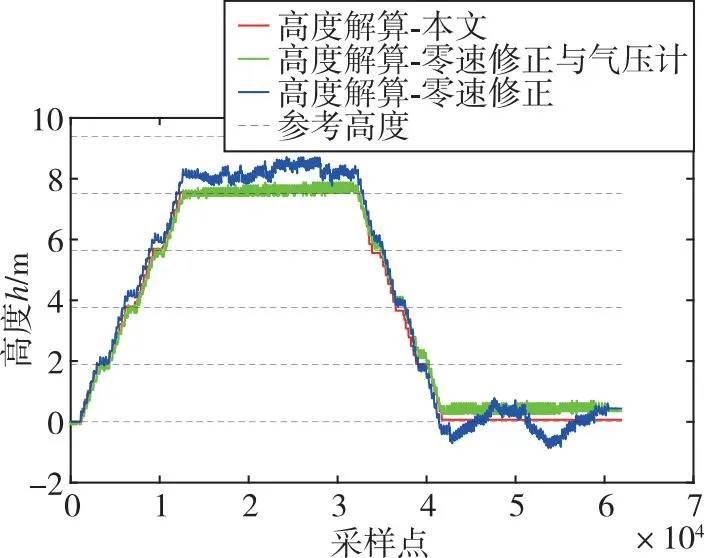
圖10 高度解算結(jié)果

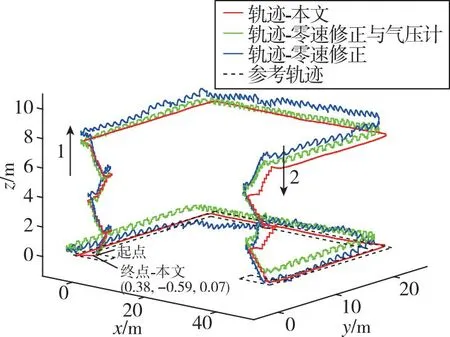
圖11 實(shí)驗(yàn)2三維運(yùn)動(dòng)軌跡

圖10中紅色線為本文的高度解算算法得到的高度結(jié)果,其終點(diǎn)高度為0.07 m,高度解算平均絕對(duì)誤差為0.06 m,每層樓的高度解算誤差比較穩(wěn)定;藍(lán)色線為利用零速修正解算算法得到的高度結(jié)果,由于加速度計(jì)數(shù)據(jù)積分存在累計(jì)誤差,導(dǎo)致高度漂移,從第三層到達(dá)第四層解算高度誤差達(dá)到最大,由第四層到達(dá)第三層時(shí),累計(jì)誤差正負(fù)抵消,高度誤差達(dá)到最小,其終點(diǎn)高度為0.43 m,高度解算平均絕對(duì)誤差為0.41 m。綠色線為利用氣壓計(jì)相對(duì)高度信息和零速修正進(jìn)行解算得到的高度結(jié)果,由于氣壓計(jì)易受到外界環(huán)境因素影響,導(dǎo)致高度解算出現(xiàn)誤差,每層樓的高度解算誤差相差較大,其終點(diǎn)高度為0.35 m,高度解算平均絕對(duì)誤差為0.17 m。基于臺(tái)階高度與足間距的高度解算算法相較于零速修正和零速修正與氣壓計(jì)聯(lián)合算法高度解算平均絕對(duì)誤差分別下降了85.37%和64.70%。

圖11中紅色軌跡為本文算法得到的三維定位結(jié)果,三維定位誤差占總路程的0.39%,相較于零速修正與氣壓計(jì)聯(lián)合算法,誤差下降了77.06%,行人在大樓內(nèi)的運(yùn)動(dòng)軌跡,航向穩(wěn)定,軌跡高度誤差小,表明該算法可以有效修正航向誤差,提高行人在大樓內(nèi)的高度計(jì)算精度,實(shí)現(xiàn)高精度行人室內(nèi)三維定位。

4 結(jié)論

本文針對(duì)基于純慣性器件的行人導(dǎo)航系統(tǒng)誤差隨時(shí)間累積致使定位精度嚴(yán)重下降的問題,提出基于足間距信息輔助的行人三維慣性定位算法。在平面運(yùn)動(dòng)和上下樓運(yùn)動(dòng)分別進(jìn)行對(duì)比實(shí)驗(yàn),實(shí)驗(yàn)數(shù)據(jù)顯示:

1)行人圍繞平面閉環(huán)路徑行走,本文算法解算的雙足導(dǎo)航系統(tǒng)閉環(huán)誤差占比平均值為0.64%,閉環(huán)誤差占比與零速修正算法相比下降55. 56%,證明足間約束模型能有效減小航向誤差。

2)在上下樓高度實(shí)驗(yàn)中,本文算法解算的高度信息絕對(duì)平均誤差為0.06 m,與零速修正算法和零速修正與氣壓計(jì)聯(lián)合算法解算高度信息相比,平均絕對(duì)誤差分別下降了85.37%和64.70%,證明通過臺(tái)階高度與足間距信息解算高度能有效減少高度漂移。

3)本文提出的算法能在保證系統(tǒng)自主性與適用性的同時(shí),有效提升足綁式IMU三維INS定位精度,能夠?qū)崿F(xiàn)導(dǎo)航誤差在總路程的0.50%以內(nèi)的三維定位,具有良好的工程應(yīng)用價(jià)值。