載人月面上升動力重構方案研究

侯振東， 劉 揚， 孫興亮， 田 林， 黃克武， 黃 震

（北京空間飛行器總體設計部， 北京 100094）

1 引言

在典型的載人月球探測模式中，航天員完成月面任務后需搭乘載人登月艙從月面起飛上升，與停泊在環月軌道的目標飛行器交會對接。 在阿波羅計劃［1］和星座計劃［2］中，載人飛船為目標飛行器。 近期美國提出重返月球的阿爾特密斯計劃［3－4］，部署月球軌道空間站以拓展任務能力，登月艙從月面上升后與月球軌道空間站交會對接。

月面動力上升過程是影響航天員安全的關鍵環節。 張磊［5］基于Gauss 偽譜法和序列二次規劃優化了月面上升過程中的燃料消耗，并針對提前與推遲條件下非共面起飛的問題，提出了上升偏航、升交點調整、傾角調整3 種方案，并分析了其適用性；李桃取等［6］針對月球大角度異面動力上升入軌問題，提出了一種基于顯式制導律和軌道機動原理，實現大角度異面上升；鞏慶海等［7］針對迭代制導在月面上升段的應用開展研究，從工程可實現性以及燃料最優角度，給出了迭代制導方案；班煥恒等［8］基于序列二階錐規劃方法，求解了直接上升交會軌跡凸優化算法，并通過包括內點法熱啟動等手段提升了求解效率。

月面動力上升過程具有執行時間短、高動態的特點，一旦發生故障導致無法繼續上升，很難在地面支持下進行故障處置，導致航天員傷亡［9－10］。為加強月面動力上升過程的應急救生能力，可設計多臺軌控發動機并聯的動力系統方案，在1 臺或多臺軌控發動機發生故障時，通過動力重構利用剩余動力系統能力繼續上升入軌。

理論上，在剩余動力系統推力超過登月艙重力時即可完成上升入軌，但在實際任務中會面臨一些問題。 Sostaric 等［11］研究表明，月面上升推進劑消耗與登月艙推重比關系密切，若動力重構后的推重比特別低，則會導致推進劑消耗急劇增加。 另外，動力重構后的上升軌跡會發生變化，進而導致入軌條件偏離標稱工況。 由于后續的交會對接過程對自主性和快速性要求較高［12－14］，需要登月艙能夠快速調整交會變軌策略，在規定時間內將航天員送返目標飛行器。

本文對載人登月艙月面上升過程的動力重構方案進行研究，通過對動力重構可靠性、應急上升推進劑消耗和飛行軌跡、應急交會對接等方面的分析，得出動力重構方案的設計要求。

2 動力重構方案設計

2.1 動力重構下的應急飛行方案

登月艙配置多臺軌控發動機，上升過程中若1 臺或多臺軌控發動機發生故障時，重新調整軌控發動機使用策略，利用剩余可用動力系統繼續上升入軌。 軌控發動機可能出現的故障模式包括閥門故障導致的發動機無法開機、燃燒室結構破壞導致的推力喪失等。

1 臺軌控發動機故障時，其余軌控發動機的推力矢量方向可能會偏離質心，引起較大的姿態干擾力矩。 為保證動力重構后姿態控制的穩定性，多臺軌控發動機應對稱布局，在1 臺發生故障后及時關閉對稱布局的軌控發動機，重新將推力矢量調整到質心附近。

動力重構下的月面上升流程如圖1 所示。 由于動力重構后登月艙的推重比發生改變，登月艙月面上升軌跡也會偏離標稱工況，關鍵參數如飛行時長、航程等均有所變化。 同時，推重比和飛行時間的變化還會導致上升過程的推進劑消耗量發生偏離。 為保證月面上升動力重構方案的可實施性，登月艙推進劑預算時需考慮這種應急工況。

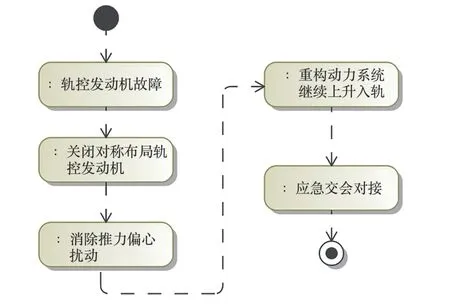
圖1 動力重構下的月面上升流程Fig.1 Lunar ascent process under propulsion recon?struction

在載人月球探測任務規劃中，登月艙從月面上升入軌后一般需盡快與駐留在環月軌道的目標飛行器完成交會對接，將航天員安全送回月軌。動力重構后，由于月面上升軌跡發生變化，交會對接初始軌道條件也區別于標稱工況。 因此，入軌后，登月艙需調整交會變軌策略，修正初始軌道偏差。

2.2 動力重構下的發動機使用策略

動力上升采用的并聯發動機配置數量需綜合考慮發動機推力偏斜、重量代價、可靠性提升程度等確定，具體分析如下：

1）發動機故障進行重構后應保證剩余發動機推力合力方向仍在登月艙質心附近，避免推力偏斜產生的干擾力矩引起登月艙失穩。 因此，發動機配置數量至少應有3 臺，若僅有2 臺，則難以保證單臺發動機故障后的姿態穩定性。

2）登月艙月面上升任務處于整個載人月球探測任務的末端，返回月軌的干重對推進劑需求量影響顯著，可達1 ∶10［15］。 因此，發動機配置數量不宜過多，降低多發動機及管路閥門等設備干重代價。 因此，發動機配置數量建議不超過5 臺。

3）發動機配置數量增加到一定程度后，不會引起系統可靠性的顯著改善，計算分析結果詳見后文。

綜上，動力重構方案采用的發動機配置數量采用3～5 臺。

登月艙軌控發動機布局方案如圖2 所示，不同數量的軌控發動機動力重構策略如下：

圖2 登月艙3～5 臺軌控發動機布局方案Fig.2 Layout of 3 to 5 orbit control thrusters for lu?nar lander

1）3 臺軌控發動機方案。 若A1故障，則登月艙發送指令關閉A1，由A2＋A3上升入軌；若A2／A3故障，則登月艙發送指令關閉A2和A3，由A1上升入軌。

2）4 臺軌控發動機方案。 若A1／A3故障，則登月艙發送指令關閉A1和A3，由A2＋A4上升入軌；若A2／A4故障，則登月艙發送指令關閉A2和A4，由A1＋A3上升入軌。

3）5 臺軌控發動機方案。 若A1故障，則登月艙發送指令關閉A1，由A2＋A3＋A4＋A5上升入軌；若A2／A4故障，則登月艙發送指令關閉A2和A4，由A1＋A3＋A5上升入軌；若A3／A5故障，則登月艙發送指令關閉A3和A5，由A1＋A2＋A4上升入軌；若A2／A4和A1均故障，則登月艙發送指令關閉A1、A2、A4，由A3＋A5上升入軌；若A3／A5和A1均故障，則登月艙發送指令關閉A1、A3、A5，由A2＋A4上升入軌；若A2～A5均故障，則登月艙發送指令關閉A2～A5，采用A1上升入軌。

需要注意的是，上述動力重構策略未考慮推進劑消耗等約束。 若重構后推重比下降較為嚴重，動力重構策略可能還需付出額外的代價。

3 動力重構可靠性評估

假設發動機不可搖擺且無推力調節能力，針對2.2 節給出的發動機配置方案進行系統可靠性建模與評估。

3.1 3 臺軌控發動機方案

記單臺軌控發動機可靠性為η，則不考慮動力重構策略時，軌控發動機系統正常工作的可靠性為η3，若考慮動力重構策略，軌控發動機系統正常工作的可靠性ηR3為式（1）：

其中右式3 項分別為A1～A3均正常工作、A1或A2或A3故障、A2和A3均故障的概率。 采用動力重構，對軌控發動機系統可靠性的提升主要通過右式第2～3 項實現。

3.2 4 臺軌控發動機方案

不考慮動力重構策略時，軌控發動機系統正常工作的可靠性為η4，若考慮動力重構策略，軌控發動機系統正常工作的可靠性ηR4為式（2）：

其中右式3 項分別為A1～A4均正常工作、A1～A4任一故障、A1和A3均故障或A2和A4均故障的概率。 采用動力重構，對軌控發動機系統可靠性的提升主要通過右式第2～3 項實現。

3.3 5 臺軌控發動機方案

不考慮動力重構策略時，軌控發動機系統正常工作的可靠性為η5，若考慮動力重構策略，軌控發動機系統正常工作的可靠性ηR5為式（3）：

其中右式4 項分別為A1～A5均正常工作、A2～A5任一故障、A2和A4均故障或A3和A5均故障或A1和A2～A5任一臺均故障、A1和A2和A4均故障或A1和A3和A5均故障、A2～A5均故障的概率。 采用動力重構，對軌控發動機系統可靠性的提升主要通過右式第2～5 項實現。

3.4 多方案對比分析

3～5 臺軌控發動機配置下，采用動力重構方案對發動機系統可靠性的貢獻見圖3。 圖例中，多機并聯是指未考慮動力重構方案，即要求所有發動機均正常工作；多機重構是指考慮動力重構方案。

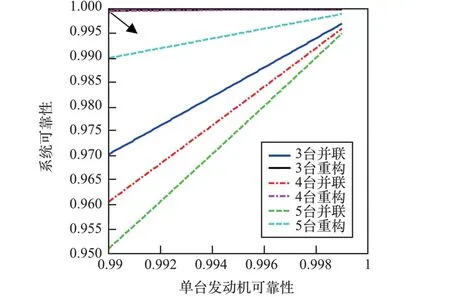
圖3 登月艙3～5 臺軌控發動機組合系統可靠性Fig.3 Reliability of thrust combination with 3 to 5 thrusters for lunar lander

由結果可見，在單臺發動機可靠性相同時，并聯工作的發動機越多，系統可靠性越低，但通過動力重構方案可大幅提高系統可靠性，特別是對于發動機配置為3 ～4 臺的方案。 在單機可靠性為0.99 時，系統可靠性可達0.9996。 5 臺發動機的動力重構方案下，系統可靠性相對較低，主要是因為5 臺發動機并聯的基礎可靠性較低，實際上根據式（2）和（3）可知，5 臺發動機的動力重構方案與4 臺發動機對系統可靠性提升的作用基本相當。 圖4 為動力重構方案對發動機系統可靠性的增幅，即動力重構方案的系統可靠性與多機并聯方案系統可靠性的差值。

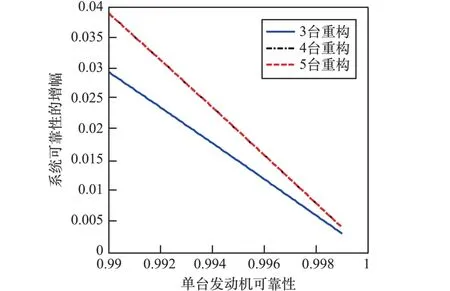
圖4 動力重構方案對多機并聯發動機組合系統可靠性的提升作用Fig.4 Reliability improvement of power reconstruc?tion for multiple engine combination

考慮到5 臺軌控發動機并聯方案的系統可靠性相對較低，且重構方案較為復雜，后續分析主要針對3 臺和4 臺軌控發動機組合方案。

4 應急上升性能分析

4.1 月面上升制導方案

登月艙在月面上升過程中，在航天員承受力學載荷范圍內一般采用最大推力飛行，以降低推進劑消耗。 月面上升一般可分為3 個階段：第1階段為垂直上升，目的是達到調姿飛行的安全高度；第2 階段為上升調姿，目標姿態為下一階段入口條件；第3 階段為軌道入射，根據制導律調整飛行姿態，以同時提高飛行速度和高度，直至達到目標入軌條件后，軌控發動機關機。

垂直上升和上升調姿飛行時間短，對月面上升特性影響較小。 為盡量降低推進劑消耗，軌道入射段采用一種最優制導律［16］，具體如下。

最短上升時間對應最優指標為J＝tf，常值推力下等價于推進劑消耗最少。 首先定義Hamilto?nian 函數如式（4）所示。

式中，λ?為協態變量，u、v、w為三軸速度，gm、rm分別為月球引力和半徑，τ為推力特性參數，θ和ψ表示待求解的最優俯仰角和偏航角。進而使用小角度假設，求解得到式（5）、（6）：

4.2 推進劑消耗分析

在上升初始推重比（地球重力）＜0.4 時，推進劑消耗隨著初始推重比降低急劇增加；初始推重比在0.5～0.6 時，上升能量最優。 理論上推重比越大，飛行時間越短，有利于減少重力損耗，從而節約推進劑消耗，但常推力上升制導需要同時保證面內終端高度與速度，但是控制量僅有俯仰角一個。 當推重比過大時，目標高度和速度不能同時滿足，反而會造成推力損耗，需要額外的推力來消除先前推力產生的多余加速度。 因而初始推重比＞0.7 時，推進劑消耗隨著初始推重比增大而緩慢上升［11］。 標稱工況設計時，選取初始推重比為0.4～0.6。

載人登月艙的重量一般要顯著高于無人探測器。 本文算例中軌控發動機選取中國嫦娥探月工程的7500 N 發動機［17］，通過多機并聯提供合適的推重比。

參考阿波羅登月艙月面上升任務，入軌目標軌道設定為15 km×80 km，入軌點為近月點。 當發生單臺或多臺軌控發動機故障時，通過動力重構繼續飛行。 由于采用能量最優制導，動力重構后沿用當前制導律，但由于推力條件發生變化，得到的制導指令與標稱工況有所區別。

設定月面上升初始時刻即發生動力系統故障，對于3 臺軌控發動機組合方案，不同初始推重比和不同重構方案下的推進劑消耗情況如圖5 所示。 圖中，橫坐標為3 臺發動機的標稱工況推重比（地球重力），對應登月艙起飛重量約3820 ～7320 kg。

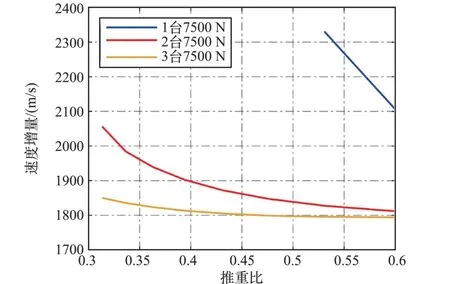
圖5 3 臺發動機動力重構方案的上升速度增量Fig.5 Ascent velocity increment for propulsion re?construction with 3 thrusters

由結果可見，1 臺發動機發生故障進行動力重構飛行時，等效速度增量高于標稱工況，但隨著初始推重比增加，等效速度增量增幅從206 m／s降至18 m／s，在初始推重比超過0.4 時，等效速度增量增幅在90 m／s 以下。 2 臺發動機發生故障進行動力重構飛行時，推力損失嚴重，在初始推重比較小時無法起飛，直至初始推重比超過0.5 時，才具備起飛能力，且等效速度增量增幅至少300 m／s，對應推進劑消耗至少200 kg（起飛重量3820 kg）。 考慮到推進劑消耗代價過大，且對起飛重量的適應能力有限，動力重構時可不考慮1臺軌控發動機起飛方案。 實際上，根據前面可靠性評估公式（1），這種重構工況對系統可靠性提升作用較小，基本不影響系統可靠性評估結果。

對于4 臺軌控發動機組合方案，不同初始推重比和不同重構方案下的推進劑消耗情況如圖6所示。 圖中，橫坐標為4 臺發動機的標稱工況推重比（地球重力），對應登月艙起飛重量約5100 ～10 200 kg。

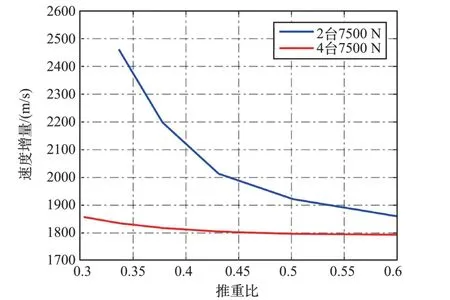
圖6 4 臺發動機動力重構方案的上升速度增量Fig.6 Ascent velocity increment for propulsion re?construction with 4 thrusters

由結果可見，1 臺發動機發生故障進行動力重構飛行時，相對于4 臺發動機標稱工況的等效速度增量增幅隨初始推重比的增加從993 m／s 降至67 m／s。 當在初始推重比超過0.4 時，等效速度增量增幅在210 m／s 以下，對應推進劑消耗約280 kg（起飛重量7650 kg）。

綜上，3 臺軌控發動機方案在動力重構時的推進劑消耗要低于4 臺軌控發動機方案，且二者的動力系統可靠性相當，但3 臺軌控發動機方案能夠適應的月面起飛重量較低。 若月面起飛重量控制在5100～7320 kg，則3 臺軌控發動機方案在推進劑消耗方面更具優勢。

4.3 飛行軌跡分析

月面動力上升過程發生動力重構后，由于推重比顯著降低，飛行時間和飛行軌跡對應的月心角均增加，主要影響后續的交會對接策略。

由于軌道入射段的制導目標未改變，入軌軌道高度和速度仍與標稱工況一致，因此交會對接初始狀態的變化主要是與目標飛行器的相位差。

參考阿波羅登月任務，目標飛行器軌道設定為100 km×100 km。 動力重構方案下，登月艙與目標飛行器的交會對接初始相位差變化情況為式（7）：

其中ΔθE－N為動力重構應急飛行與正常飛行交會對接初始相位差的偏差， ΔθE－N＞0 表明應急飛行的初始相位差更大，即更滯后于目標飛行器，ΔθE－N＜0 則表明更接近目標飛行器。tE和tN分別為應急飛行和正常飛行的上升入軌時間，ωt為目標飛行器軌道角速度，φE和φN分別為應急飛行和正常飛行的飛行軌跡月心角。

設定月面上升初始時刻即發生動力系統故障，對于3 臺軌控發動機組合方案，不同初始推重比和不同重構方案下ΔθE－N的變化情況如圖7所示。

圖7 3 臺發動機動力重構方案的入軌相位差偏差Fig.7 Error of injection phase error for propulsion reconstruction with 3 thrusters

由結果可見，動力重構應急飛行的入軌相位差均比標稱工況大。 1 臺發動機發生故障時，隨著初始推重比的增加， ΔθE－N從8.8°降至3.3°；2 臺發動機發生故障時，在滿足上升條件時，ΔθE－N從22.8°降至16.5°。

設定月面上升初始時刻即發生動力系統故障，對于4 臺軌控發動機組合方案，不同初始推重比和不同重構方案下ΔθE－N的變化情況如圖8所示。

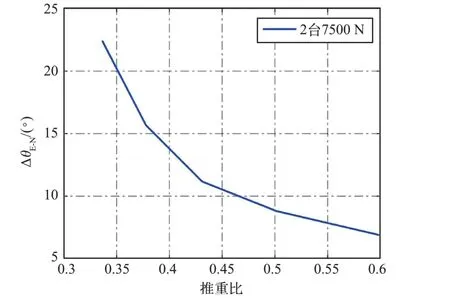
圖8 4 臺發動機動力重構方案的入軌相位差偏差Fig.8 Error of injection phase error for propulsion reconstruction with 4 thrusters

由結果可見，動力重構應急飛行的入軌相位差均比標稱工況大。 隨著初始推重比的增加，ΔθE－N從22.4°降至6.9°，相位滯后程度要大于3臺軌控發動機方案。

5 應急交會對接策略分析

月面上升入軌后，交會對接策略一般是先抬高近月點高度，再逐步調整登月艙飛行軌道，在軌道差與相位差縮小至一定范圍時，采用蘭伯特交會或霍曼轉移到達目標飛行器附近，最后再完成近距離控制和對接［11－13］。

為解決動力重構應急入軌后相位差滯后的問題，盡量減少對標稱交會對接策略的改變，設計2種應急交會對接策略，分析時設定目標飛行器駐留軌道為100 km 圓軌道。

5.1 低軌追及策略

低軌追及策略是利用與目標飛行器的高低軌角速度差，通過延長交會對接時長實現，優點是對標稱變軌策略的改動較小，缺點是飛行時間較長，航天員消耗物資會增加。

設定登月艙在15 km×80 km 的入軌軌道進行相位補償。 對于3 臺軌控發動機方案，不考慮1 臺發動機工作的重構模式，根據圖7 的仿真結果分析可知，登月艙在入軌軌道多飛行0.4 ～1.08 h 后即可實現相位補償。 由于登月艙位于橢圓軌道，若飛行時間增量不是軌道周期的整數倍，則登月艙的絕對相位也會發生變化，后續交會變軌策略也需調整。

為此設定在登月艙進入80 km×80 km 的調相軌道后進行相位補償，則對于3 臺軌控發動機方案，不考慮1 臺發動機工作的重構模式，需要在調相軌道多飛行1.09 ～2.90 h，約為0.5 ～1.5 個軌道周期。 對于4 臺軌控發動機方案，需要在調相軌道多飛行2.27 ～7.38 h，約為1 ～3.5 個軌道周期。

綜上，若采用低軌追及策略，對于3 臺軌控發動機方案，飛行時間增加不多；對于4 臺軌控發動機方案，在起飛重量較大時，飛行時間增加較多，導致物資消耗代價較大。 除上述低軌追及策略外，也可增加1 次軌控將近月點抬升至15 ～80 km，以調整相位補償時間為軌道周期整數倍，之后再抬升近月點高度至80 km 的調相軌道，可縮短相位補償時間。

5.2 蘭伯特交會策略

蘭伯特交會策略是在交會變軌末期，利用蘭伯特交會策略補償相位差，優點是基本不改變飛行時長，缺點是變軌速度增量較大。

設定在登月艙進入80 km×80 km 的調相軌道后進行蘭伯特交會。 設定標稱工況下末段變軌采用霍曼轉移策略從80 km 圓軌道轉移至100 km 圓軌道，則霍曼轉移初始時刻登月艙相位滯后于目標飛行器1.5°，所需速度增量9.0 m／s。

對于3 臺軌控發動機方案，采用蘭伯特交會策略時，變軌初始時刻登月艙相位滯后4.8°～10.3°，所需速度增量49.9 ～134.0 m／s。 對于4 臺軌控發動機方案，采用蘭伯特交會策略時，變軌初始時刻登月艙相位滯后8.4°～23.9°，所需速度增量104.0 ～366.5 m／s。

綜上，單獨采用蘭伯特變軌策略的速度增量需求較大。 實際應用時，可結合低軌追及策略和蘭伯特變軌策略實施，以權衡速度增量和飛行時間需求。

5.3 飛船應急交會

當登月艙由于敏感器故障或推進系統故障不具備主動交會能力時，也可以有飛船進行應急交會。 其變軌策略為通過霍曼變軌在1 個軌道周期完成圓軌道向低軌圓軌道調整的過程，期間完成面外第一次修正，低軌軌道高度確定依據與著陸器初始相位差、應急任務時間約束和燃料約束進行選擇。 到達登月艙后下方約50 km 位置，隨后轉入近距離自主控制段。

考慮初始條件飛船位于登月艙后方的100 km×100 km 近圓軌道，登月艙位于15 km×80 km 軌道，相位差20°，則在第一個拱點處將半長軸調整至約1780 km，通過1 ～1.5 個軌道周期滿足近距離交會的初始條件，總的速度增量為27 m／s。

6 結論

1）對于多臺軌控發動機方案，動力重構可提供動力系統可靠性。 對于3 ～4 臺軌控發動機方案，在單機可靠性為0.99 時，系統可靠性可達0.9996。

2）動力重構應急飛行的推進劑消耗會有所增加，3 臺軌控發動機方案要優于4 臺，但可適應的月面起飛重量較低。 若單機選用7500 N 發動機，則月面起飛重量在5100 ～7320 kg 范圍時，優選3 臺軌控發動機方案。

3）動力重構應急飛行會導致登月艙入軌相位與目標飛行器的滯后幅度增大，可綜合低軌追及策略和蘭伯特交會策略進行相位補償。

4）在進行登月艙動力重構設計時，還可考慮采用大推力姿控發動機輔助方式進一步降低應急上升推進劑消耗，同時大推力姿控發動機還可兼顧克服多臺軌控發動機開機干擾力矩。