不確定性中的確定性?
——中國經(jīng)濟風險識別

隋建利 呂文強 劉金全

一、引言

近年來，伴隨著中美貿(mào)易摩擦、新冠肺炎疫情等一系列極端風險事件的發(fā)生，中國經(jīng)濟穩(wěn)增長壓力日益增加。國家統(tǒng)計局發(fā)布的數(shù)據(jù)顯示，2023 年第三季度中國GDP 同比增長4.9%，增速較2023 年第二季度回落1.4%，意味著現(xiàn)階段中國經(jīng)濟的增長壓力及增長風險仍在進一步上升。面對世界經(jīng)濟復(fù)蘇緩慢、全球疫情持續(xù)演變、外部環(huán)境紛繁復(fù)雜的現(xiàn)實，如何抵御風險的滲透沖擊，保持經(jīng)濟平穩(wěn)健康的發(fā)展態(tài)勢，關(guān)乎當下的國計民生。2023 年《政府工作報告》明確指出，目前中國經(jīng)濟正面臨需求收縮、供給沖擊、預(yù)期轉(zhuǎn)弱“三重壓力” 的嚴峻形勢，必須正視外部與內(nèi)部不確定性的交織，在不確定性中謀求確定性，從而有效應(yīng)對各種風險挑戰(zhàn)，保持經(jīng)濟在合理區(qū)間運行。2023 年12 月，習近平總書記在中央經(jīng)濟工作會議上再次強調(diào)，要以經(jīng)濟安全為基礎(chǔ)，堅持“穩(wěn)” 字當頭、穩(wěn)中求進的工作總基調(diào)，著力防范和化解重大經(jīng)濟風險，進而實現(xiàn)“穩(wěn)增長” 與“防風險” 的雙重目標。可以看出，有關(guān)不確定性與經(jīng)濟風險之間關(guān)系的討論，已然成為國家和政府各部門關(guān)注的重要議題。在此背景下，探究不確定性對經(jīng)濟風險的潛在影響，對于深入貫徹黨的二十大精神，強化風險監(jiān)管與預(yù)期管理，促進經(jīng)濟高質(zhì)量發(fā)展與高水平安全良性互動，實現(xiàn)中國式現(xiàn)代化具有重要的指導(dǎo)意義。

不確定性能夠?qū)?jīng)濟主體的投資與消費決策產(chǎn)生重要影響，繼而與經(jīng)濟增長存在顯著關(guān)聯(lián)(Bloom 等，2018)，因此不少研究聚焦于探索不確定性影響經(jīng)濟增長的理論機制。其中，不確定性對經(jīng)濟增長的傳導(dǎo)途徑存在四種不同的理論邏輯，分別為具有促進作用的Hartman-Abel 效應(yīng)理論和增長期權(quán)理論，以及具有抑制作用的實物期權(quán)理論和風險規(guī)避理論。具體而言，Hartman-Abel 效應(yīng)理論是指，在企業(yè)能夠根據(jù)經(jīng)濟形勢靈活調(diào)整生產(chǎn)規(guī)模的情況下，伴隨著不確定性的升高，企業(yè)會更加關(guān)注隨之而來的投資機會與潛在利潤，這使得企業(yè)的期望邊際收益得以增加，從而對經(jīng)濟增長產(chǎn)生積極影響(Hartman，2006)。增長期權(quán)理論是指，未來前景不確定性使得企業(yè)為了實現(xiàn)長期生產(chǎn)經(jīng)營，不斷加大研發(fā)投入，以期保證產(chǎn)品或服務(wù)的持續(xù)創(chuàng)新，這可視為增長期權(quán)的積累過程，可以為企業(yè)帶來較高的預(yù)期利潤，進而促進經(jīng)濟增長(Smit 等，2017；顧夏銘等，2018)。實物期權(quán)理論是指，經(jīng)濟主體的投資與消費機會可被視作一系列實物期權(quán)，不確定性的增加會使經(jīng)濟主體看跌期權(quán)價值，從而延遲投資與消費，最終引致經(jīng)濟增速下降(劉貫春等，2022)。風險規(guī)避理論是指，對于投資者而言，不確定性使得投資者要求更高的風險補償，導(dǎo)致企業(yè)融資約束及成本提高，進而引發(fā)金融市場收緊(Lhuissier 和Tripier，2021；Di Maggio 等，2022；譚小芬等，2022)；對于消費者而言，不確定性能夠誘發(fā)消費者的預(yù)防性儲蓄和風險厭惡偏好，降低消費者投資、消費意愿，繼而抑制經(jīng)濟增長(Mumtaz 和Theodoridis，2018；Angelini 等，2019)。然而，盡管上述理論研究成果豐碩，但是都無一例外地將不確定性視為獨立于經(jīng)濟主體的外生變量，鮮有研究從企業(yè)行為等微觀視角出發(fā)，探究經(jīng)濟系統(tǒng)中不確定性的生成機制，以及其影響經(jīng)濟增長的微觀機理。

在探究不確定性影響經(jīng)濟增長的相關(guān)研究中，不確定性指標的選取至關(guān)重要。部分學者通過計算單一宏觀變量的波動性來衡量不確定性，例如采用股票市場指數(shù)、通貨膨脹以及GDP 等變量的波動率作為經(jīng)濟不確定性的代理指標(Chen 等，2020；王曉宇和楊云紅，2021)。盡管計算簡單方便，但是基于波動性的測度方法沒有剔除宏觀變量的可預(yù)期成分，這與不確定性的本質(zhì)，即經(jīng)濟系統(tǒng)中無法預(yù)期的部分并不相符。為了克服上述局限，國內(nèi)外學者從不確定性的定義出發(fā)，利用GARCH 以及VAR 族等計量模型對宏觀變量的預(yù)測誤差進行估計，并將預(yù)測誤差作為不確定性的代理指標。具體地，已有研究使用股票收益率、利率以及工業(yè)增加值等變量的條件波動率來反映不確定性水平(王義中和宋敏，2014；Scotti，2016)。盡管預(yù)測誤差能夠充分體現(xiàn)不確定性中的“非預(yù)期性”，但是具體的預(yù)測誤差可能過度依賴于特定的經(jīng)濟指標，因此這種度量方式難以表征經(jīng)濟系統(tǒng)整體的不確定性水平。有鑒于此，Jurado 等(2015)基于高維因子模型對大規(guī)模經(jīng)濟變量的非預(yù)期條件波動率進行估計，并測度經(jīng)濟系統(tǒng)中不可預(yù)測成分的共同波動，即經(jīng)濟不確定性。此后，相關(guān)研究運用高維因子模型分別衡量了中國的經(jīng)濟不確定性水平(Huang 等，2018；趙文佳和梁燚焱，2020)與金融不確定性水平(黃卓等，2018)。然而，通過梳理能夠發(fā)現(xiàn)，已有研究多聚焦于經(jīng)濟不確定性的度量，而對金融不確定性的測度分析明顯偏少。事實上，無論是就產(chǎn)生機理、波動特征還是經(jīng)濟效應(yīng)而言，經(jīng)濟不確定性與金融不確定性都存在著顯著差異(Alessandri 和Mumtaz，2019；Ludvigson 等，2021)，但是，國內(nèi)文獻目前對此明顯探究不足。

隨著不確定性對宏觀經(jīng)濟的影響日趨復(fù)雜，基于不同視角探究不確定性影響經(jīng)濟增長的實證研究不斷涌現(xiàn)。國內(nèi)外學者運用傳統(tǒng)計量模型以及動態(tài)隨機一般均衡(DSGE)模型等方法，分析了不確定性對經(jīng)濟增長的沖擊效應(yīng)。結(jié)果發(fā)現(xiàn)，不確定性對實體經(jīng)濟表現(xiàn)出明顯的逆周期性，能夠?qū)?jīng)濟增速產(chǎn)生顯著的負向影響(Hristov 和Roth，2022；王博和徐飄洋，2022)。然而，相關(guān)研究均是從點估計的視角出發(fā)，在本質(zhì)上揭示的是不確定性對經(jīng)濟增長“期望值” 的影響，而忽略了從區(qū)間估計的視角探究不確定性對經(jīng)濟增長“風險值” 的潛在影響。事實上，伴隨著外部環(huán)境的深刻變化，全球經(jīng)濟形勢愈加復(fù)雜。在此背景下，刻畫不同風險水平下經(jīng)濟增長的運行狀況，揭示經(jīng)濟增長的潛在風險變得極為重要。有鑒于此，國際貨幣基金組織(IMF)根據(jù)在險價值(value at risk，VaR)的概念提出了在險增長(growth at risk，GaR)，即將經(jīng)濟增長視為一種概率分布形式，并利用相應(yīng)的條件變量來預(yù)測未來經(jīng)濟增長的概率分布曲線，旨在衡量宏觀金融形勢對經(jīng)濟風險的潛在影響(IMF，2017)。Adrian 等(2019)從經(jīng)濟增長概率分布出發(fā)，運用條件分位數(shù)回歸模型，分析了經(jīng)濟和金融狀況對經(jīng)濟風險的相關(guān)影響。隨后，國外學者基于概率分布的視角，探究了不同宏觀變量對經(jīng)濟風險的影響作用(Adams 等，2021；Jovanovic 和Ma，2022)。反觀國內(nèi)的研究領(lǐng)域，目前僅有張曉晶和劉磊(2020)從概率分布的視角，探討了金融風險對經(jīng)濟增長特定“風險值” 的影響，而現(xiàn)有文獻缺乏對經(jīng)濟風險的系統(tǒng)性分析，亦缺少探究不確定性對經(jīng)濟風險的影響研究。

通過梳理已有文獻能夠發(fā)現(xiàn)，現(xiàn)有研究仍存在一定的局限性。首先，以往研究大多將不確定性視為獨立于經(jīng)濟系統(tǒng)的外生沖擊，未能從經(jīng)濟主體層面探究不確定性的生成機制，因而無法將不確定性與經(jīng)濟增長置于統(tǒng)一的內(nèi)生框架分析其內(nèi)在機理。其次，已有研究多采用經(jīng)濟不確定性及其代理指標檢驗不確定性的經(jīng)濟效應(yīng)，鮮有文獻在大數(shù)據(jù)估計的基礎(chǔ)上，基于中國經(jīng)濟不確定性與金融不確定性的分離測度視角，探究其對經(jīng)濟風險的異質(zhì)性影響。最后，既有研究多基于傳統(tǒng)計量模型展開，從點估計的視角出發(fā)，分析不確定性對經(jīng)濟增長“期望值” 的沖擊效應(yīng)，鮮有研究基于區(qū)間估計的視角，將經(jīng)濟增長視作一種概率分布形式，探究不確定性對經(jīng)濟風險的潛在影響。

鑒于上述分析，本文具有如下可能的創(chuàng)新:第一，提出內(nèi)生不確定性的概念，并將經(jīng)濟增長視為一種概率分布形式，基于不確定性與經(jīng)濟增長的統(tǒng)一分析框架，闡明不確定性影響預(yù)期經(jīng)濟增速分布的理論機制。第二，基于高維因子模型，構(gòu)建中國經(jīng)濟不確定性與金融不確定性指數(shù)，進而辨析經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險的異質(zhì)性影響。第三，運用條件分位數(shù)回歸模型，分別將經(jīng)濟不確定性與金融不確定性作為預(yù)期經(jīng)濟增速分布的條件變量，繼而通過在險增長、相對熵值以及期望損失等模型，揭示不確定性沖擊下經(jīng)濟風險的確定性特征。第四，基于理論模型與經(jīng)驗事實的綜合分析，探究不確定性對經(jīng)濟風險的時變沖擊效應(yīng)，刻畫不確定性對經(jīng)濟風險的驅(qū)動機制。因此，本文研究具有如下的貢獻與價值:在理論意義層面，引入內(nèi)生不確定性概念以及經(jīng)濟增長的概率分布形式，豐富不確定性影響經(jīng)濟增長的微觀理論基礎(chǔ)，拓寬相關(guān)領(lǐng)域的研究視角和研究思路；在現(xiàn)實意義層面，分離構(gòu)建并探究經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險的潛在影響，不僅有助于中國應(yīng)對“三重壓力”，防范和化解重大經(jīng)濟金融風險，保障經(jīng)濟運行在合理區(qū)間，而且能夠為中國各部門推出有利于經(jīng)濟穩(wěn)定的政策提供重要的理論依據(jù)與經(jīng)驗支持。

二、理論模型

為了從理論上刻畫不確定性的產(chǎn)生及其對經(jīng)濟增長的影響，本文參考Jovanovic 和Ma(2022)，將不確定性與經(jīng)濟增長置于統(tǒng)一框架下，構(gòu)建涵括內(nèi)生不確定性的經(jīng)濟增長模型。其中，理論模型具有一個重要特征，即不確定性與經(jīng)濟增長均為內(nèi)生變量，不確定性來源于經(jīng)濟系統(tǒng)中技術(shù)水平的更新過程。

(一)代表性廠商

考慮一個具有消費偏好的代表性廠商，其目標是最大化終生效用，目標函數(shù)可表示為:

在此，E0代表期望算子；β為跨期貼現(xiàn)率，以反映未來效用與當期效用之間的替代彈性；ct表示廠商在第t期的實際消費。假定廠商只生產(chǎn)一種商品，產(chǎn)出水平取決于技術(shù)水平A和技能組合h。其中，技能組合在本質(zhì)上強調(diào)的是技術(shù)水平與投入要素(包括勞動和資本投入)之間的匹配程度，匹配程度越高，技能組合越優(yōu)，產(chǎn)出水平越高。因此，潛在產(chǎn)出yp能夠表示為:

其中，sA表示與技術(shù)水平A相匹配的最優(yōu)技能組合，具體表示能夠在技術(shù)水平A下實現(xiàn)最大產(chǎn)出的技能組合。λ代表懲罰系數(shù)，h′為當期技術(shù)水平的實際技能組合，λ(sAh′)2/2 刻畫了廠商實際技能組合與最優(yōu)技能組合間存在的“技能缺口” 導(dǎo)致的損耗產(chǎn)出。廠商能夠選擇以x(x≥0)的速度提高其技術(shù)水平，從當期的技術(shù)水平A開始，下一期的技術(shù)水平A′可以表示為:

在此，考慮到更新后的技術(shù)水平與廠商現(xiàn)有投入要素的稟賦匹配程度是不可預(yù)測的，即更新后的新技術(shù)與先前投入要素的匹配程度既可能升高又可能降低，并且只有在廠商采用新技術(shù)之后，技術(shù)對投入要素的需求才會清晰展現(xiàn)。因此，本文假定更新的技術(shù)水平A′對最優(yōu)技能組合的影響是隨機的，即sA′服從隨機游走分布:

其中，ε～F(ε)，服從均值為0、方差為σ2的獨立同分布。廠商在觀察到ε前選擇是否更新技術(shù)，一旦更新到技術(shù)水平A′，廠商就無法再采用上一期的技術(shù)水平A。因此，假定廠商以技能組合h開始進行生產(chǎn)，進一步地，廠商可以選擇調(diào)整技能組合至h′。在此過程中，h′＝h＋Δ，假定廠商更新技術(shù)水平以及技能組合存在投入成本C(yp，Δ)，并且投入成本與潛在產(chǎn)出水平以及更新技能組合的變化幅度密切相關(guān)，其能夠表示為:

因此，廠商的凈產(chǎn)出可以表示為:

其中，u＝SA－h(huán)是最優(yōu)技能組合與實際技能組合之間的差值(以下簡稱“技能缺口”)。

(二)內(nèi)生不確定性

廠商的狀態(tài)可以利用技能缺口u與技術(shù)水平A表示，廠商的決策為(x，Δ)。此外，廠商沒有任何形式的資產(chǎn)，其消費與產(chǎn)出水平相等。因此，廠商的最優(yōu)動態(tài)方程為:

進一步地，可以得到:

并且，φ＝(λα2＋θ(1－α)2)/2。

廠商以不變速度x更新技術(shù)水平，其中，更新技術(shù)水平與技能組合的直接成本Δ與當期的技能缺口u成正比。根據(jù)式(4)，技能缺口u服從AR(1)過程:

由于廠商的狀態(tài)可以利用技能缺口u與技術(shù)水平A表示，廠商的決策為(x，Δ)。對于技能缺口u＝sA－h(huán)而言，最優(yōu)技能組合sA的變化取決于廠商決策x，而實際技能組合h則取決于廠商選擇的投入成本決策Δ。能夠發(fā)現(xiàn)，技能缺口u是經(jīng)濟系統(tǒng)中的內(nèi)生變量。因此，本文利用內(nèi)生技能缺口u的方差對不確定性進行刻畫。由于α介于0 至1 之間，技能缺口ut是平穩(wěn)的，其方差為:

其中，式(13)中的第三個等式由式(8)推導(dǎo)得到。直觀而言，σ減小能夠?qū)е聏增加，使得廠商技術(shù)水平的更新速度加快。同時，技術(shù)更新加速會導(dǎo)致技能組合SA′更加難以預(yù)測，從而致使技能缺口的方差增加。需要注意的是，正是由于廠商的行為，尤其是廠商更新技術(shù)的投資決策(x，Δ)，使得技能缺口存在波動，進而導(dǎo)致經(jīng)濟運行產(chǎn)生相應(yīng)的不確定性。不難發(fā)現(xiàn)，不確定性來源于經(jīng)濟系統(tǒng)內(nèi)部廠商的技術(shù)更迭。進一步地，考慮將經(jīng)濟中的代表性廠商擴展為無限個，全部廠商起始時都處于相同狀態(tài)(u，A)，假定所有廠商都進行相同決策，均衡將完全對稱，此時經(jīng)濟中只存在總體風險。而在每個時點上，對于全部廠商而言，x的選擇和ε的觀測值將完全一致，調(diào)整技能組合h將無法使其獲利。

(三)預(yù)期經(jīng)濟增速分布

假定C(yp，Δ)完全由技術(shù)水平與技能組合調(diào)整引致的產(chǎn)出損耗構(gòu)成，能夠得到總產(chǎn)出的對數(shù)值:

其中，φ＝(λα2＋θ(1－α)2)/2。式(14)表明，產(chǎn)出水平取決于常數(shù)項A0、時間趨勢項t以及技能缺口。因此，本文可以利用包含常數(shù)項和時間趨勢項的回歸模型估計lnyt。式(14)中，技能缺口的平方項可以解釋為預(yù)測誤差。由于ut是平穩(wěn)的，因此lnyt同樣趨勢平穩(wěn)，其趨勢為產(chǎn)出水平的長期增長率x。進一步地，經(jīng)濟增長可以表示為:

式(15)表明，經(jīng)濟增長不僅取決于技術(shù)水平的更新速度x，而且還會受到技能缺口平方項變動的影響。不難發(fā)現(xiàn)，技能缺口的減小能夠促進經(jīng)濟增長，然而，調(diào)整技能組合需要付出成本，特別是當下一期的技能組合出現(xiàn)意外降低時，產(chǎn)出水平將明顯下降。因此可以推斷，當參數(shù)θ較大時，經(jīng)濟增速分布具有負向偏斜傾向。具體地，在初始產(chǎn)出水平y(tǒng)0與技術(shù)水平A0的條件下，εt服從正態(tài)分布N(0，σ2)，預(yù)期經(jīng)濟增速分布gt可以表示為:

其中，ξt～N(0，1)，并且考慮到φ>0，ξt服從正態(tài)分布，服從自由度為1的卡方分布，因此，預(yù)期經(jīng)濟增速分布gt負向偏斜，并且服從非中心化的卡方分布。本文使用非中心化卡方分布中不同分位數(shù)的估計值，能夠得到預(yù)期經(jīng)濟增速分布的相關(guān)表達式，具體包括5%分位數(shù)的預(yù)期經(jīng)濟增速χt、預(yù)期經(jīng)濟增速均值E(gt＋1)、預(yù)期經(jīng)濟增速波動率V(gt＋1)以及預(yù)期經(jīng)濟增速分布的4 分位距IQR(gt＋1)。需要說明的是，遵循Adrian 等(2019)，本文將t期的在險經(jīng)濟增長率χt定義為t＋1 期預(yù)期經(jīng)濟增速分布的下5%分位數(shù)(即5%分位數(shù)的預(yù)期經(jīng)濟增速)，以表征經(jīng)濟下行風險。因此，在均衡狀態(tài)下，預(yù)期經(jīng)濟增速的相關(guān)分布滿足:

因此，根據(jù)式(17)至式(20)可知，5%分位數(shù)和均值預(yù)期經(jīng)濟增速伴隨著不確定性的升高而下降，預(yù)期經(jīng)濟增速分布的波動率和4 分位距則伴隨著不確定性的升高而增加，即:

當時間趨于無窮時，即在長期的預(yù)期經(jīng)濟增速分布gt中，經(jīng)濟增速不取決于初值u0，而是滿足:

其中，當且僅當α<1 時，上述預(yù)期經(jīng)濟增速的相關(guān)分布有界，能夠表示為:

lim

三、中國經(jīng)濟不確定性與金融不確定性的指數(shù)構(gòu)建

(一)不確定性指數(shù)的構(gòu)建方法

為構(gòu)建中國經(jīng)濟不確定性與金融不確定性指數(shù)，本文參考Jurado 等(2015)的研究，通過建立高維因子模型，實現(xiàn)對經(jīng)濟不確定性與金融不確定性水平的分離測度。具體而言，對于一個經(jīng)濟或金融變量序列yit，其未來n期的不確定性Uy jt(n)可以表示為只包含變量yit非預(yù)期成分的條件波動率:

其中，yit∈Rt，F(xiàn)t，而Rt和Ft分別表示經(jīng)濟和金融層面的變量信息集，E[?｜It]表示基于t時期預(yù)測信息集It的條件期望。具體地，預(yù)測信息集It由Xt＝(X1t，…，XNt)構(gòu)成。因此，條件期望E[?｜It]和yit＋n的值可以通過高維因子模型和擴散指數(shù)預(yù)測進行估計:

其中，Xit為預(yù)測信息集，ft為潛在的共同因子，表示系數(shù)矩陣，表示誤差項。對于式(29)而言，yjt為每個經(jīng)濟或金融變量序列。為了控制非線性效應(yīng)，模型中同時控制了共同因子ft的平方項kt，為預(yù)測誤差。以及(L)分別為滯后L期的系數(shù)矩陣的有限多項式，在此，本文選取滯后期L＝6 進行估計。隨后，通過對經(jīng)濟變量和金融變量的非預(yù)期條件波動率(n)進行等權(quán)平均(wj＝1/Ny)加總，即可構(gòu)建經(jīng)濟不確定性指數(shù)和金融不確定性指數(shù):

根據(jù)上述內(nèi)容不難發(fā)現(xiàn)，不確定性指數(shù)的合成方法在考慮變量波動時剔除了相應(yīng)的預(yù)期成分。事實上，這種測度方式與理論模型中不確定性τ的構(gòu)造(即“技能缺口” 的方差)在本質(zhì)上完全一致，進而有效地實現(xiàn)了理論模型與實證數(shù)據(jù)的有機銜接。

(二)數(shù)據(jù)選擇與處理

對于經(jīng)濟不確定性與金融不確定性的測度，本文參考黃卓等(2018)以及趙文佳和梁燚焱(2020)的指標構(gòu)成，選取90 維經(jīng)濟變量信息集(Rt)，170 維金融變量信息集(Ft)，以及291 維預(yù)測變量信息集(Xt)(見表1)。其中，預(yù)測變量信息除包括經(jīng)濟變量信息集和金融變量信息集外，還包括31 維經(jīng)濟政策變量信息集。本文所使用的變量選用2002 年1 月至2022 年9 月間的月度數(shù)據(jù)。不確定性指數(shù)的原始變量數(shù)據(jù)來源于中經(jīng)網(wǎng)統(tǒng)計數(shù)據(jù)庫、Wind 數(shù)據(jù)庫以及銳思數(shù)據(jù)庫。

表1 中國經(jīng)濟不確定性與金融不確定性的指標構(gòu)建

就數(shù)據(jù)處理而言，本文首先對上述291 維預(yù)測變量信息集中的274 維中國經(jīng)濟金融變量進行了新年效應(yīng)處理，使得各變量從前一年12 月至當年1 月的增長率等于當年1 月至2 月的增長率。其次，對產(chǎn)出、消費以及投資等具有趨勢性的變量進行了物價平減和X－12 季節(jié)調(diào)整，消除了價格因素和季節(jié)因素。再次，為了滿足時間序列的平穩(wěn)性要求，本文基于單位根檢驗結(jié)果，對非平穩(wěn)變量進行一階差分處理后轉(zhuǎn)換為平穩(wěn)序列。最后，為了消除量綱的影響，本文對所有序列均進行標準化處理。

(三)中國經(jīng)濟不確定性與金融不確定性的波動態(tài)勢分析

在上述不確定性指數(shù)構(gòu)造方法的基礎(chǔ)上，考慮到隨著預(yù)測步長的增加，不確定性的平均水平將逐漸提高，而其變異程度則將有所下降。因此，本文選取預(yù)測步長n為6 期(即計算未來6 個月的不確定性指數(shù))，以此構(gòu)建中國經(jīng)濟不確定性與金融不確定性指數(shù)。需要說明的是，為了探究不確定性與經(jīng)濟增長的深層次關(guān)系，本文對月度頻率的不確定性指數(shù)進行了加權(quán)處理，將其轉(zhuǎn)換為2002 年第一季度至2022 年第三季度的季度不確定性指數(shù)，結(jié)果如圖1 所示。

圖1 中國經(jīng)濟不確定性與金融不確定性指數(shù)

圖1 展示出中國經(jīng)濟不確定性與金融不確定性的時變動態(tài)，總體而言，經(jīng)濟不確定性與金融不確定性的變動趨勢較為一致。其中，不確定性自2002 年開始持續(xù)降低，直至2006年附近接近波谷。隨后，不確定性日漸增加，于全球金融危機期間達到階段峰值。伴隨著金融危機的結(jié)束，不確定性逐漸下降，進而長期處于低水平的震蕩區(qū)間。2018 年伊始，受中美貿(mào)易摩擦深化影響，不確定性呈現(xiàn)出螺旋式上升趨勢。此后，疊加新冠肺炎疫情等極端風險事件，不確定性水平屢創(chuàng)新高。

此外，觀察經(jīng)濟不確定性與金融不確定性的演化軌跡不難發(fā)現(xiàn)，盡管二者的總體波動趨勢十分相似，但具體的波動過程不盡相同。例如，2015 年，受中國股票市場劇烈波動影響，金融不確定性水平大幅上升，而同期基于實體經(jīng)濟層面的經(jīng)濟不確定性則無任何明顯波動。進一步地，比較二者的波動特征還能夠發(fā)現(xiàn)，金融不確定性的波動更為頻繁、劇烈，并且當經(jīng)濟系統(tǒng)中的不確定性水平出現(xiàn)大幅波動時，金融不確定性的變動通常領(lǐng)先于經(jīng)濟不確定性。這意味著，相較于經(jīng)濟不確定性，金融不確定性能夠作為更好的經(jīng)濟預(yù)測先行指標，更加敏銳地捕捉經(jīng)濟發(fā)展狀況的階段性趨勢與動向。

四、不確定性視閾下中國經(jīng)濟風險的確定性識別

為了揭示預(yù)期經(jīng)濟增長的時變運行區(qū)間，識別不確定性視閾下中國經(jīng)濟風險的波動特征，進而探究經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險的潛在影響，本文擬通過構(gòu)建基于不確定性條件的預(yù)期經(jīng)濟增速分布，從在險增長、相對熵值以及期望損失模型等多維視角，實現(xiàn)對經(jīng)濟風險的有效識別與測度，刻畫不確定性沖擊下經(jīng)濟風險的確定性規(guī)律。

(一)基于在險增長模型的中國經(jīng)濟風險識別

與衡量金融風險的在險價值模型相類似，在險增長模型旨在衡量未來經(jīng)濟增長的風險值。具體地，在險增長采用經(jīng)濟增長概率分布中分位數(shù)的值，即預(yù)期經(jīng)濟增速分布中不同分位數(shù)對應(yīng)的經(jīng)濟增速水平予以度量。不同風險概率下的在險增長水平(即不同分位數(shù)的預(yù)期經(jīng)濟增速水平)能夠反映不同的經(jīng)濟含義，進而實現(xiàn)對經(jīng)濟風險的有效測度。例如，5%分位數(shù)的預(yù)期經(jīng)濟增速為a，表示未來經(jīng)濟增速有5%的概率低于a，即有95%的概率高于a；同理，95%分位數(shù)的預(yù)期經(jīng)濟增速為b，表示未來經(jīng)濟增速有95%的概率低于b。因此，低分位數(shù)與高分位數(shù)的預(yù)期經(jīng)濟增速本質(zhì)上反映的是，在一定風險(置信)水平下，未來經(jīng)濟增速的下限值與上限值，即經(jīng)濟下行風險與經(jīng)濟上行風險。

為了估計基于不確定性條件的預(yù)期經(jīng)濟增速分布，通常需要進行兩步計算。第一步是通過分位數(shù)回歸獲取一些重要分位點的回歸結(jié)果，即估計出預(yù)期經(jīng)濟增速分布的部分結(jié)果；第二步是將得到的部分回歸結(jié)果共同映射到偏態(tài)t分布中，進而擬合形成完整的預(yù)期經(jīng)濟增速分布。因此，本文首先構(gòu)建如下條件分位數(shù)回歸模型:

其中，xt為解釋變量，包括常數(shù)項、當期實際經(jīng)濟增速①本文選取2002 第一季度至2022 第三季度的GDP 同比實際增速作為當期實際經(jīng)濟增速。(控制變量)以及不確定性指數(shù)。為辨析中國經(jīng)濟不確定性和金融不確定性對預(yù)期經(jīng)濟增速分布的異質(zhì)性影響，本文分別以經(jīng)濟不確定性和金融不確定性為條件變量構(gòu)建分位數(shù)回歸模型。yqt＋m為未來m期的預(yù)期經(jīng)濟增速，具體可劃分為不同的分位數(shù)q。δq為系數(shù)矩陣，其行和列分別表示不同分位數(shù)和不同解釋變量的回歸系數(shù)。m為預(yù)測期數(shù)，本文采用季度數(shù)據(jù)，選取預(yù)測期m＝4(即四個季度)，以期探究不確定性沖擊的潛在影響。在分位數(shù)回歸模型中，δq的估計值應(yīng)使得殘差的分位數(shù)加權(quán)絕對值最小:

其中，Π(?)為指示函數(shù)，若括號內(nèi)邏輯關(guān)系成立，指示函數(shù)為1，反之則為0。式(32)使得殘差絕對值能夠根據(jù)殘差項的大小被賦予不同權(quán)重。由此，可以得到xt對yt＋m的條件分位數(shù):

1.預(yù)期經(jīng)濟增速與不確定性的相關(guān)性檢驗

為了直觀地刻畫不同分位數(shù)預(yù)期經(jīng)濟增速與不確定性的關(guān)系，本文初步描繪了預(yù)期經(jīng)濟增速與不確定性的散點圖。進一步地，運用條件分位數(shù)回歸模型分別擬合出5%、50% (即中位數(shù))以及95%分位數(shù)預(yù)期經(jīng)濟增速對不確定性的回歸擬合直線。此外，為了與不同分位數(shù)的擬合直線進行對比，本文還刻畫了預(yù)期經(jīng)濟增速對不確定性的OLS 估計結(jié)果。其中，圖2 展示出預(yù)期經(jīng)濟增速與經(jīng)濟不確定性的散點圖，圖3 繪制出預(yù)期經(jīng)濟增速與金融不確定性的散點圖。

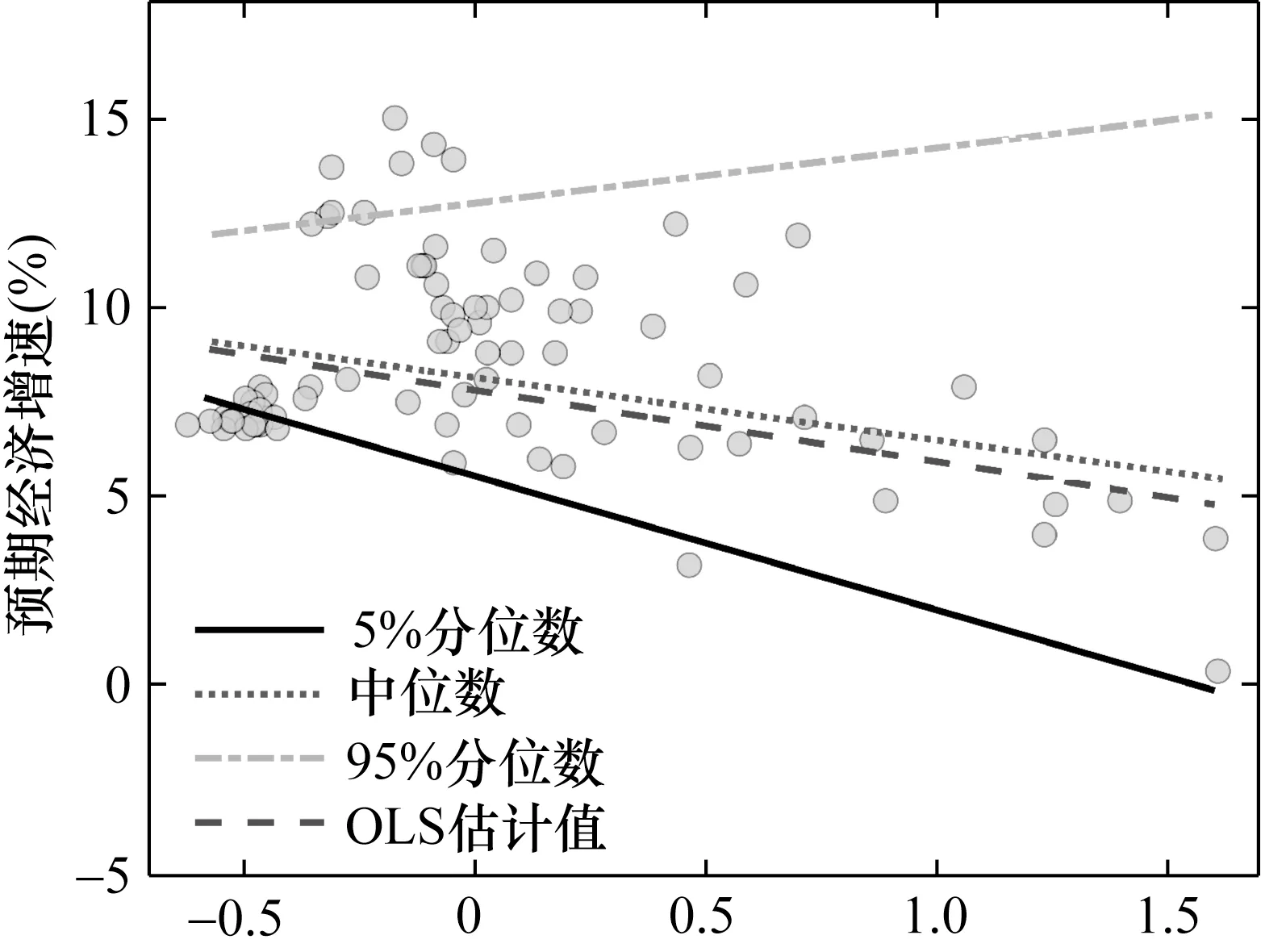
圖2 預(yù)期經(jīng)濟增速與經(jīng)濟不確定性散點圖

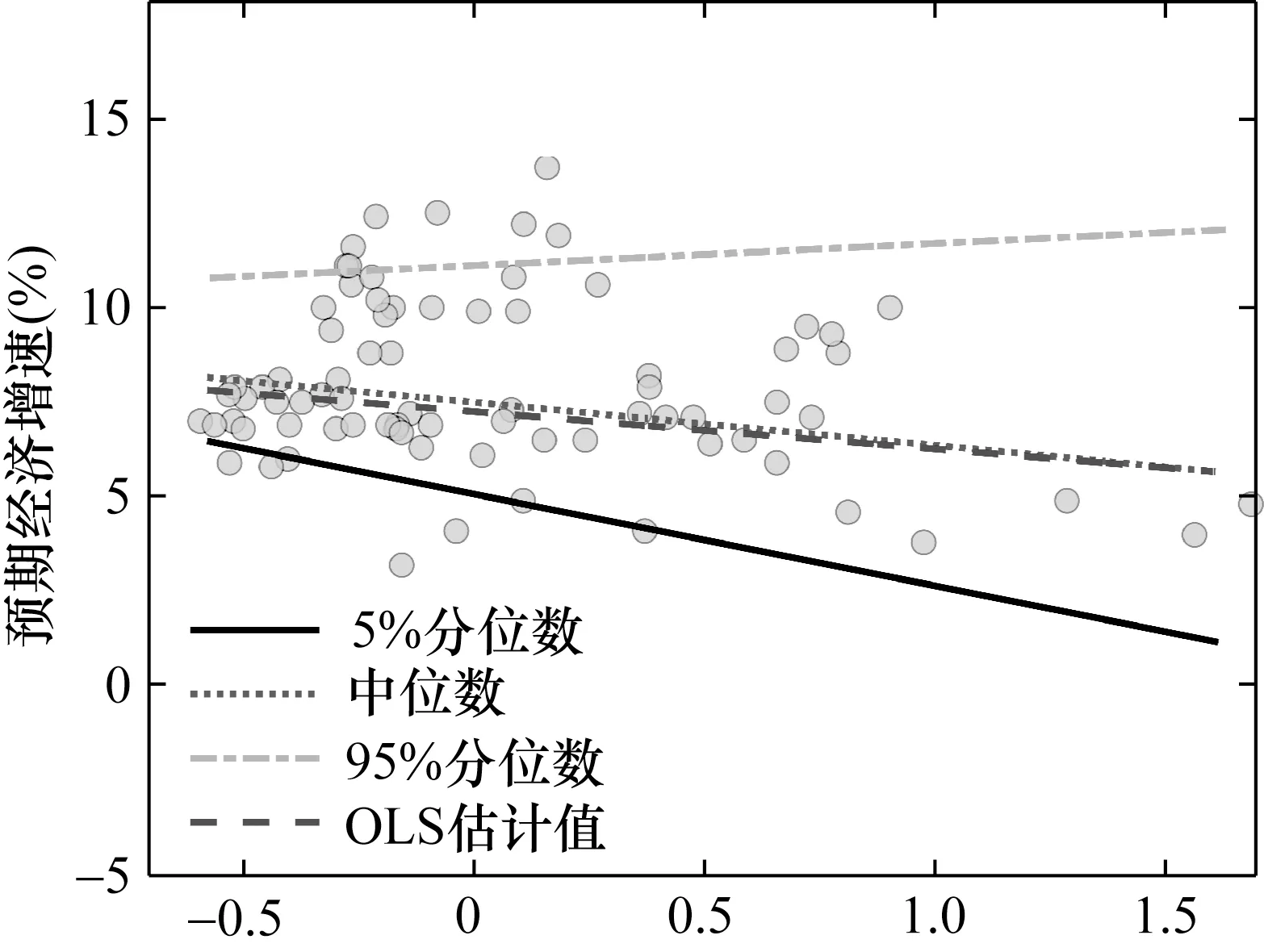
圖3 預(yù)期經(jīng)濟增速與金融不確定性散點圖

觀察圖2 與圖3 不難發(fā)現(xiàn)，一方面，預(yù)期經(jīng)濟增速對經(jīng)濟不確定性與金融不確定性的回歸擬合直線具有明顯的共性特征。具體而言，95%分位數(shù)預(yù)期經(jīng)濟增速的回歸斜率顯著為正，而5%分位數(shù)、中位數(shù)以及OLS 回歸的擬合斜率則顯著為負。這意味著，不同分位數(shù)預(yù)期經(jīng)濟增速與不確定性的相關(guān)關(guān)系明顯不同。其中，不確定性的升高使得高分位數(shù)的預(yù)期經(jīng)濟增速有所增加，同時引致低分位數(shù)的預(yù)期經(jīng)濟增速不斷下滑。另一方面，基于經(jīng)濟不確定性與金融不確定性的回歸擬合結(jié)果存在顯著的異質(zhì)性特征。從5%分位數(shù)、中位數(shù)以及95%分位數(shù)預(yù)期經(jīng)濟增速的回歸斜率來看，相較于金融不確定性，經(jīng)濟不確定性的影響相對更大。這表明，經(jīng)濟不確定性能夠更為顯著地升高預(yù)期經(jīng)濟增速的上限值，同時還可以更為明顯地降低預(yù)期經(jīng)濟增速的下限值。此外，從預(yù)期經(jīng)濟增速對不確定性的OLS 估計結(jié)果來看，經(jīng)濟不確定性的負向影響同樣更為顯著。因此，可以判斷，與金融不確定性相比，經(jīng)濟不確定性的經(jīng)濟效應(yīng)明顯較大，能夠造成更為劇烈的經(jīng)濟波動。

2.預(yù)期經(jīng)濟增速的分位數(shù)回歸估計

根據(jù)條件分位數(shù)回歸模型，本文能夠進一步估計出預(yù)期經(jīng)濟增速對當期經(jīng)濟增速和不確定性的回歸系數(shù)。圖4 與圖5 分別展示出基于經(jīng)濟不確定性與金融不確定性條件的分位數(shù)回歸結(jié)果。具體而言，圖4(a)與圖5(a)描繪了當期經(jīng)濟增速對預(yù)期經(jīng)濟增速的影響，圖4(b)與圖5(b)刻畫了不確定性對預(yù)期經(jīng)濟增速的影響。其中，X軸表示不同分位數(shù)，Y軸為分位數(shù)回歸的系數(shù)估計結(jié)果，OLS 估計值反映解釋變量對預(yù)期經(jīng)濟增速均值的回歸系數(shù)結(jié)果，深色陰影部分面積為系數(shù)估計結(jié)果的置信區(qū)間。①圖中陰影面積為零假設(shè)的95%置信區(qū)間，零假設(shè)假定不確定性與經(jīng)濟增長之間符合線性關(guān)系。特別地，本文使用不確定性和實際經(jīng)濟增速的全樣本演化來估計具有四階滯后、高斯分布和一個常數(shù)的向量自回歸(VAR)，并利用1 000 個樣本進行bootstrap 計算不同置信水平下的邊界。

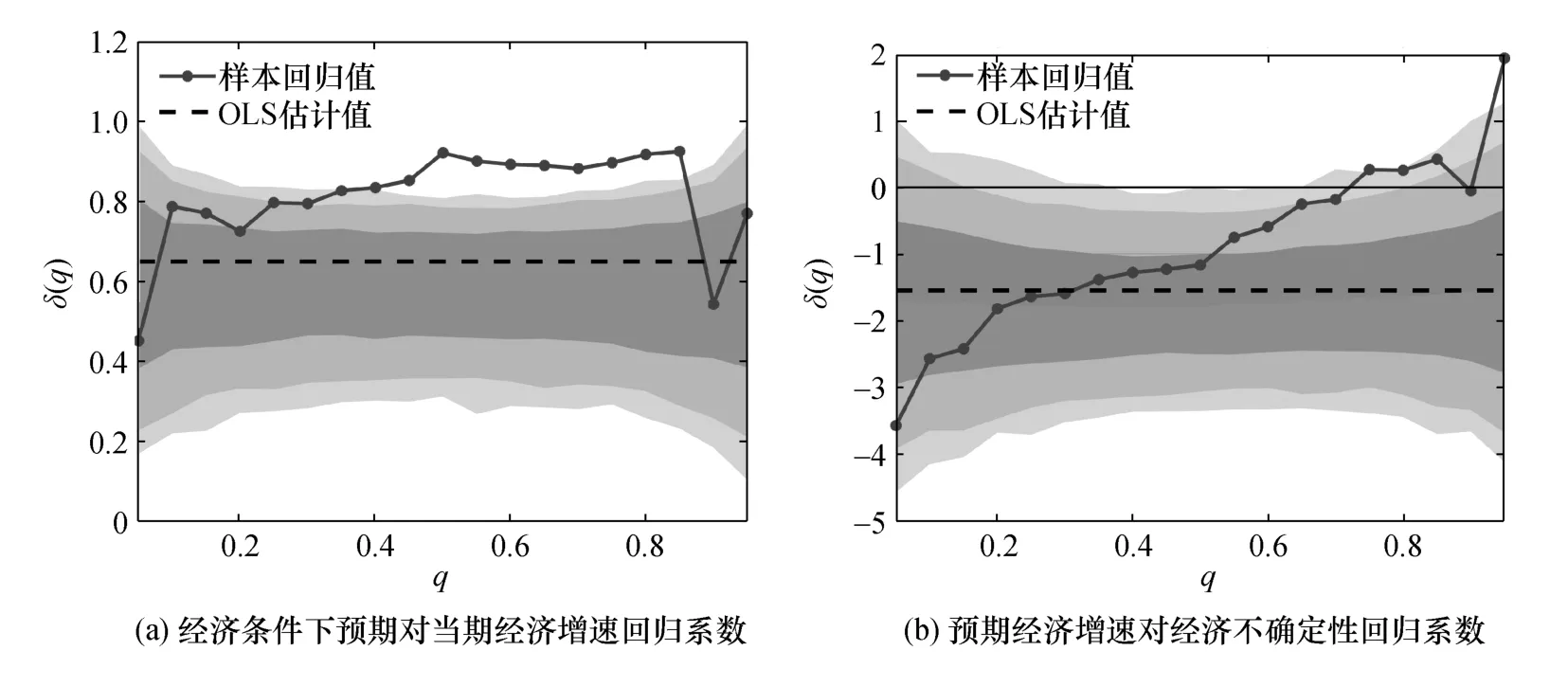
圖4 基于經(jīng)濟不確定性條件的分位數(shù)回歸系數(shù)結(jié)果

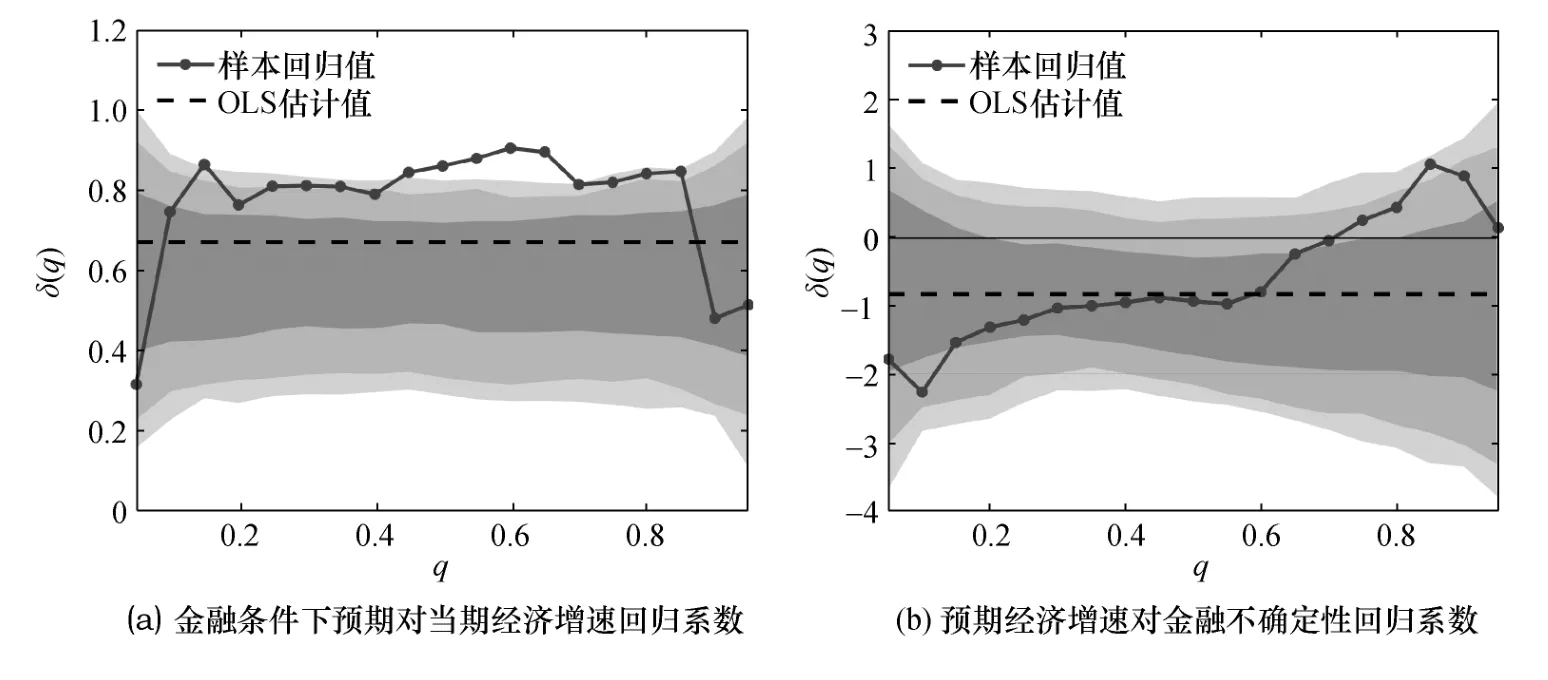
圖5 基于金融不確定性條件的分位數(shù)回歸系數(shù)結(jié)果

觀察圖4(a)與圖5(a)中的樣本回歸系數(shù)能夠發(fā)現(xiàn)，無論是以經(jīng)濟不確定性還是金融不確定性為條件變量，當期經(jīng)濟增速對不同分位數(shù)預(yù)期經(jīng)濟增速的影響均較為穩(wěn)定，始終圍繞在0.6 的回歸系數(shù)值附近。形成鮮明對比的是，根據(jù)圖4(b)與圖5(b)可知，低分位數(shù)至高分位數(shù)向上傾斜的回歸系數(shù)走勢表明，與高分位數(shù)的預(yù)期經(jīng)濟增速相比較，不確定性對低分位數(shù)預(yù)期經(jīng)濟增速具有更大的負向作用。這意味著，不確定性對經(jīng)濟風險具有明顯的非對稱性影響。其中，不確定性能夠?qū)ξ磥斫?jīng)濟增速的下限值產(chǎn)生更為顯著的負向沖擊，從而引致更大的經(jīng)濟下行風險。

對比圖4(b)與圖5(b)的樣本回歸系數(shù)不難看出，經(jīng)濟不確定性對低分位數(shù)預(yù)期經(jīng)濟增速的回歸系數(shù)接近－4，約是金融不確定性影響系數(shù)的二倍。這表明，相較于金融不確定性，經(jīng)濟不確定性能夠?qū)ξ磥斫?jīng)濟增速的下限值產(chǎn)生更強的驅(qū)動力，致使經(jīng)濟潛存更大的下行風險。此外，從圖中的OLS 估計值來看，經(jīng)濟不確定性對預(yù)期經(jīng)濟增速均值的負向影響同樣更為劇烈。追根溯源，經(jīng)濟不確定性能夠通過實物期權(quán)效應(yīng)和風險規(guī)避效應(yīng)，對經(jīng)濟主體的投資與消費意愿產(chǎn)生明顯的抑制作用，從而對宏觀基本面的投資、消費、進出口以及就業(yè)等方面造成顯著的負面沖擊，引致經(jīng)濟增速迅速下降。同時，經(jīng)濟增速的下降與經(jīng)濟不確定性的增加之間還存在著明顯的“自我強化” 機制，即經(jīng)濟不確定性的提高會導(dǎo)致經(jīng)濟增速的下降，而經(jīng)濟增速下降又會反過來進一步推升經(jīng)濟不確定性，從而造成經(jīng)濟不確定性對經(jīng)濟增速的二次沖擊，由此加劇經(jīng)濟不確定性的負向影響。就金融不確定性對經(jīng)濟增速的影響而言，一方面，根據(jù)金融摩擦機制，金融不確定性能夠顯著降低金融部門的風險承擔能力以及風險承擔意愿，進而通過融資風險溢價的波動對信貸規(guī)模造成負向影響，沖擊企業(yè)層面的生產(chǎn)經(jīng)營，最終導(dǎo)致經(jīng)濟活動相應(yīng)收縮；另一方面，金融不確定性可以通過金融市場傳導(dǎo)至實體經(jīng)濟層面，推動經(jīng)濟不確定性水平的提高，繼而間接影響經(jīng)濟增速變動。因此，分析上述影響機制可以發(fā)現(xiàn)，經(jīng)濟不確定性與經(jīng)濟增速更為密切相關(guān)，能夠?qū)?jīng)濟增速產(chǎn)生更加顯著的負向沖擊。

3.基于在險增長模型的中國經(jīng)濟風險走勢判斷

正如前文所述，不確定性對經(jīng)濟風險具有明顯的非對稱影響。那么，經(jīng)濟上行及下行風險是否會因此呈現(xiàn)出相似的非對稱性特征? 鑒于此，本文基于在險增長模型，在圖6 與圖7 中分別描繪經(jīng)濟不確定性與金融不確定性條件下預(yù)期經(jīng)濟增速的時變走勢，從而直觀地體現(xiàn)中國經(jīng)濟風險的波動路徑。圖中虛線(即陰影部分邊緣)從下至上分別刻畫了預(yù)期經(jīng)濟增速的條件5%、10%、25%、75%、90%以及95%分位數(shù)走勢，實線描繪了預(yù)期經(jīng)濟增速的條件中位數(shù)走勢。

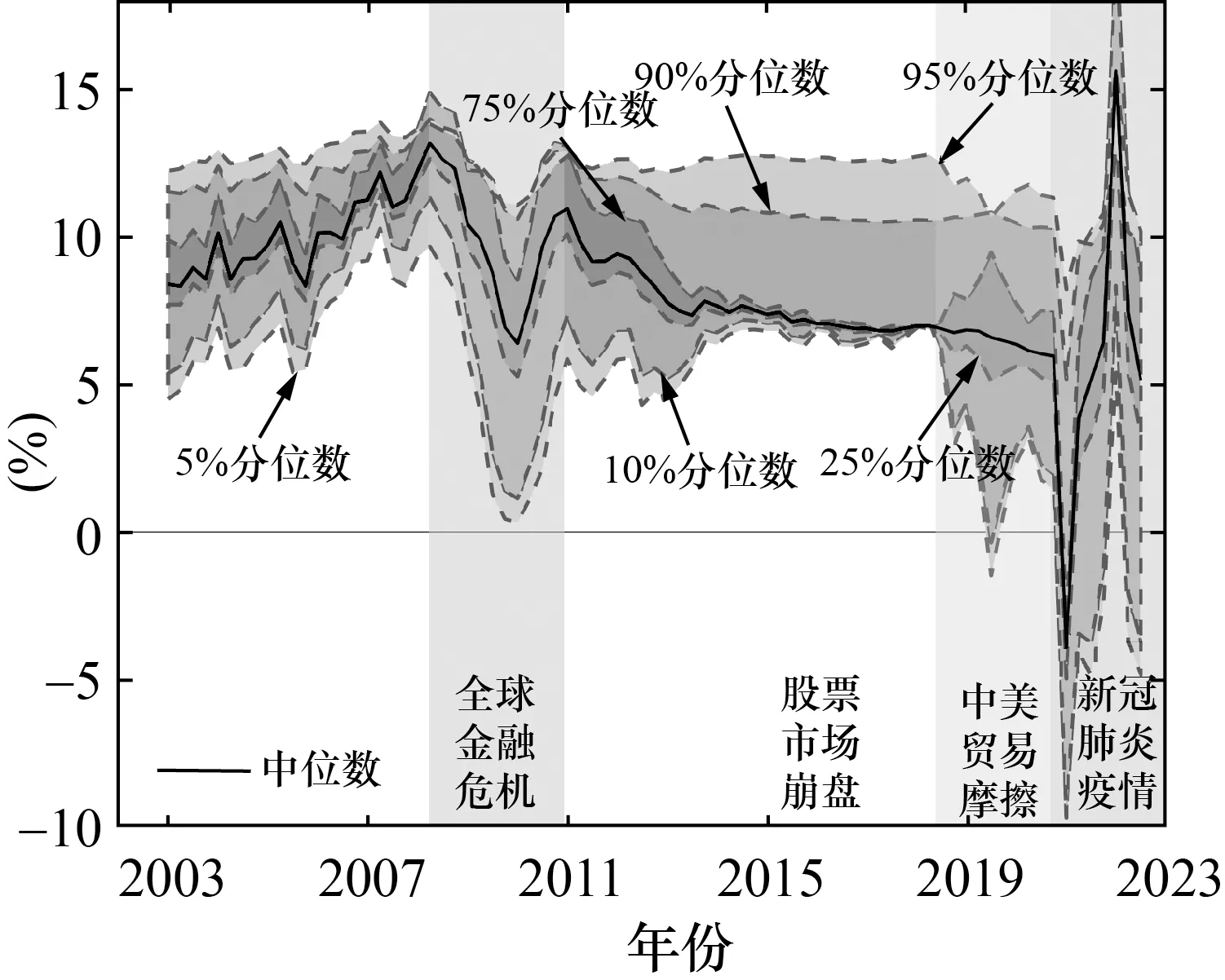
圖6 經(jīng)濟不確定性條件下預(yù)期經(jīng)濟增速走勢

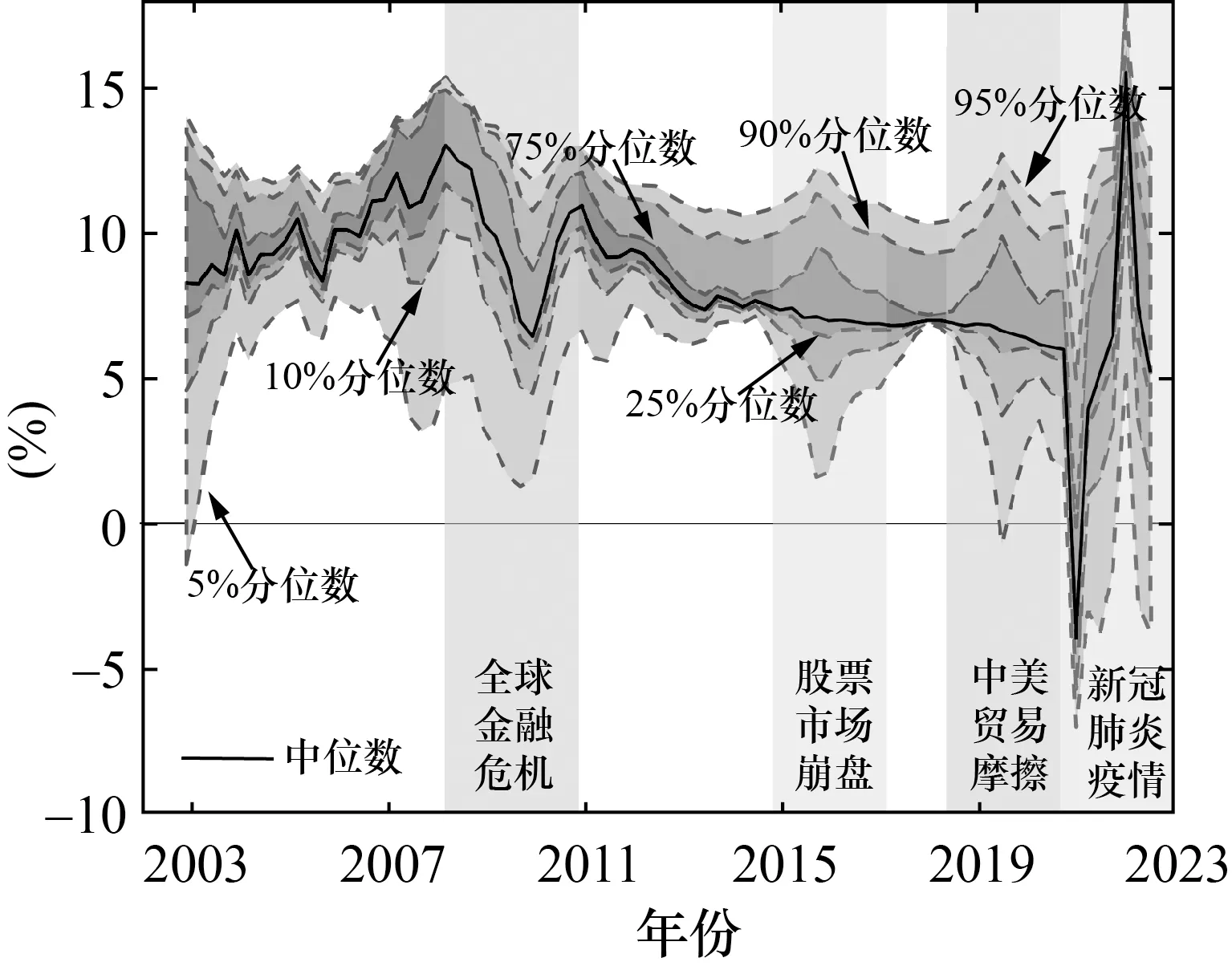
圖7 金融不確定性條件下預(yù)期經(jīng)濟增速走勢

觀察圖6 能夠發(fā)現(xiàn)，不同分位數(shù)預(yù)期經(jīng)濟增速的總體趨勢基本一致，但是波動幅度明顯不同。具體而言，在全球金融危機以及新冠肺炎疫情期間，低分位數(shù)的預(yù)期經(jīng)濟增速出現(xiàn)了巨幅下跌，而高分位數(shù)預(yù)期經(jīng)濟增速則僅呈現(xiàn)相應(yīng)的微幅下降。此外，在中美貿(mào)易摩擦期間，低分位數(shù)的預(yù)期經(jīng)濟增速快速滑落至零水平附近，而高分位數(shù)的預(yù)期經(jīng)濟增速卻表現(xiàn)出較小幅度的上漲。從圖7 可以看出，金融不確定性與經(jīng)濟不確定性條件下的預(yù)期經(jīng)濟增速走勢總體上較為相似；不同的是，基于金融不確定性條件的預(yù)期經(jīng)濟增速除了在全球金融危機、中美貿(mào)易摩擦以及新冠肺炎疫情期間呈現(xiàn)顯著的非對稱波動，還對2015 年的股市崩盤產(chǎn)生了明顯響應(yīng)。彼時，低分位數(shù)的預(yù)期經(jīng)濟增速大幅下降，接近金融危機時期的極低水平，而高分位數(shù)預(yù)期經(jīng)濟增速則表現(xiàn)出不同程度的意外上升。

綜觀圖6 與圖7 不難發(fā)現(xiàn)，預(yù)期經(jīng)濟增速分布走勢呈現(xiàn)出明顯的非對稱性特征，即低分位數(shù)的預(yù)期經(jīng)濟增速隨著時間的推移變動異常劇烈，而高分位數(shù)的預(yù)期經(jīng)濟增速則相對平穩(wěn)，并且當經(jīng)濟處于極端風險階段時，這種非對稱性特征更為明顯。事實上，這完全可以根據(jù)圖4(b)與圖5(b)中的分位數(shù)回歸結(jié)果予以解釋，即不確定性能夠?qū)Φ头治粩?shù)的預(yù)期經(jīng)濟增速產(chǎn)生更為顯著的負向影響。因此，這意味著，伴隨著不確定性水平的升高，經(jīng)濟上行及下行風險會呈現(xiàn)出異質(zhì)性的響應(yīng)過程，致使經(jīng)濟風險具有明顯的非對稱性特征。并且，當經(jīng)濟步入風險階段時，劇烈增加的不確定性會驅(qū)使非對稱性特征更為顯著。需要注意的是，從中美貿(mào)易摩擦以及股市崩盤的時點來看，伴隨著低分位數(shù)預(yù)期經(jīng)濟增速的大幅降低，高分位數(shù)預(yù)期經(jīng)濟增速還可能出現(xiàn)小幅上漲。這意味著，不確定性沖擊在顯著降低未來經(jīng)濟增速下限值的同時，還可能引致經(jīng)濟增速的上限值微幅上升，這同樣與前文中不確定性對部分高分位數(shù)預(yù)期經(jīng)濟增速的回歸系數(shù)為正的結(jié)果相符。究其原因，不確定性沖擊一方面可以抑制經(jīng)濟行為主體的投資和消費意愿，另一方面還可以激發(fā)企業(yè)層面探索性研究的創(chuàng)新活力，從而產(chǎn)生促進經(jīng)濟發(fā)展的增長期權(quán)效應(yīng)。因此，不確定性可能兼具正向影響和負向影響，能夠?qū)?jīng)濟增長產(chǎn)生極為復(fù)雜的交互作用，進而引致不同分位數(shù)預(yù)期經(jīng)濟增速的異質(zhì)性響應(yīng)。此外，對比圖6 與圖7 可知，基于經(jīng)濟不確定性條件的低分位數(shù)預(yù)期經(jīng)濟增速波動得更為劇烈。例如，2020 年新冠肺炎疫情期間，基于經(jīng)濟不確定性的低分位數(shù)預(yù)期經(jīng)濟增速大幅降至－10%，而基于金融不確定性的低分位數(shù)預(yù)期經(jīng)濟增速則保持在－5%的水平附近。這進一步印證了經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險的異質(zhì)性影響，即經(jīng)濟不確定性能夠引致更大的經(jīng)濟下行風險，致使經(jīng)濟表現(xiàn)出更為悲觀的增速預(yù)期。

(二)中國經(jīng)濟風險中的確定性特征識別

基于在險增長模型的結(jié)果表明，不確定性對經(jīng)濟風險具有明顯的非對稱影響。其中，伴隨著不確定性水平的升高，經(jīng)濟下行風險顯著增加，而經(jīng)濟上行風險則較為穩(wěn)定，從而致使經(jīng)濟風險表現(xiàn)出明顯的非對稱性特征。然而，在險增長模型僅是基于未來經(jīng)濟增長風險值的視角，實現(xiàn)對經(jīng)濟風險的衡量。事實上，經(jīng)濟風險還可以利用預(yù)期經(jīng)濟增速分布尾部區(qū)域的脆弱性進行測度。因此，本文將根據(jù)分位數(shù)回歸結(jié)果，擬合形成完整的預(yù)期經(jīng)濟增速分布，以期進一步量化經(jīng)濟上行及下行風險，繼而識別不確定性沖擊下經(jīng)濟風險的確定性特征，具體過程如下。

首先，將分位數(shù)回歸得到的系數(shù)矩陣代入式(33)，可以得到分位數(shù)的近似估計和累積分布函數(shù)。此后，為使用概率密度函數(shù)擬合分位數(shù)回歸的估計結(jié)果，本文引入Azzalini和Capitanio (2003)提出的偏態(tài)t分布，其概率密度函數(shù)可以表示為:

其中，t(?)和T(?)分別表示偏態(tài)t分布的概率密度函數(shù)和累積分布函數(shù)。偏態(tài)t分布包含四個參數(shù)，分別為分布的期望μ、標準差ω、偏度η以及自由度υ。事實上，偏態(tài)t分布本質(zhì)上就是在t分布的基礎(chǔ)上引入了表示偏度的參數(shù)η。當η＝0 時，偏態(tài)t分布能夠退化為傳統(tǒng)t分布；當η＝0 且υ＝∞時，偏態(tài)t分布可以進一步退化為正態(tài)分布；當η≠0 且υ＝∞時，偏態(tài)t分布可以轉(zhuǎn)變?yōu)槠龖B(tài)分布。接下來，令條件分位數(shù)xt)與偏態(tài)t分布累積分布函數(shù)的反函數(shù)F－1(q；μ，ω，η，υ)之間的距離平方和最小，能夠估計出偏態(tài)t分布的四個參數(shù):

1.預(yù)期經(jīng)濟增速的時變運行區(qū)間刻畫

根據(jù)估計出的偏態(tài)t分布參數(shù)，本文可以在圖8 與圖9 中描繪出基于不確定性條件的時變預(yù)期經(jīng)濟增速分布結(jié)果。其中，X軸表示預(yù)期經(jīng)濟增速，Y軸為時間，Z軸為預(yù)期經(jīng)濟增速分布的概率密度函數(shù)。不難發(fā)現(xiàn)，預(yù)期經(jīng)濟增速的分布結(jié)果與圖6 及圖7 中的預(yù)期經(jīng)濟增速走勢在總體上較為相似。事實上，圖8 與圖9 能夠更為直觀地反映未來經(jīng)濟增速的區(qū)間變動。其中，經(jīng)濟不確定性條件下的經(jīng)濟增速區(qū)間跨度相對較大，并且具有明顯的時變特征；而金融不確定性條件下的經(jīng)濟增速區(qū)間則相對集中，并且表現(xiàn)出較強的穩(wěn)定性。

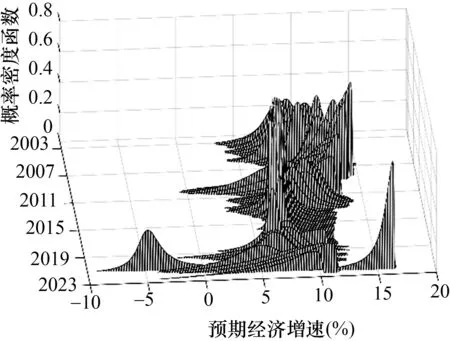
圖8 經(jīng)濟不確定性條件下預(yù)期經(jīng)濟增速分布

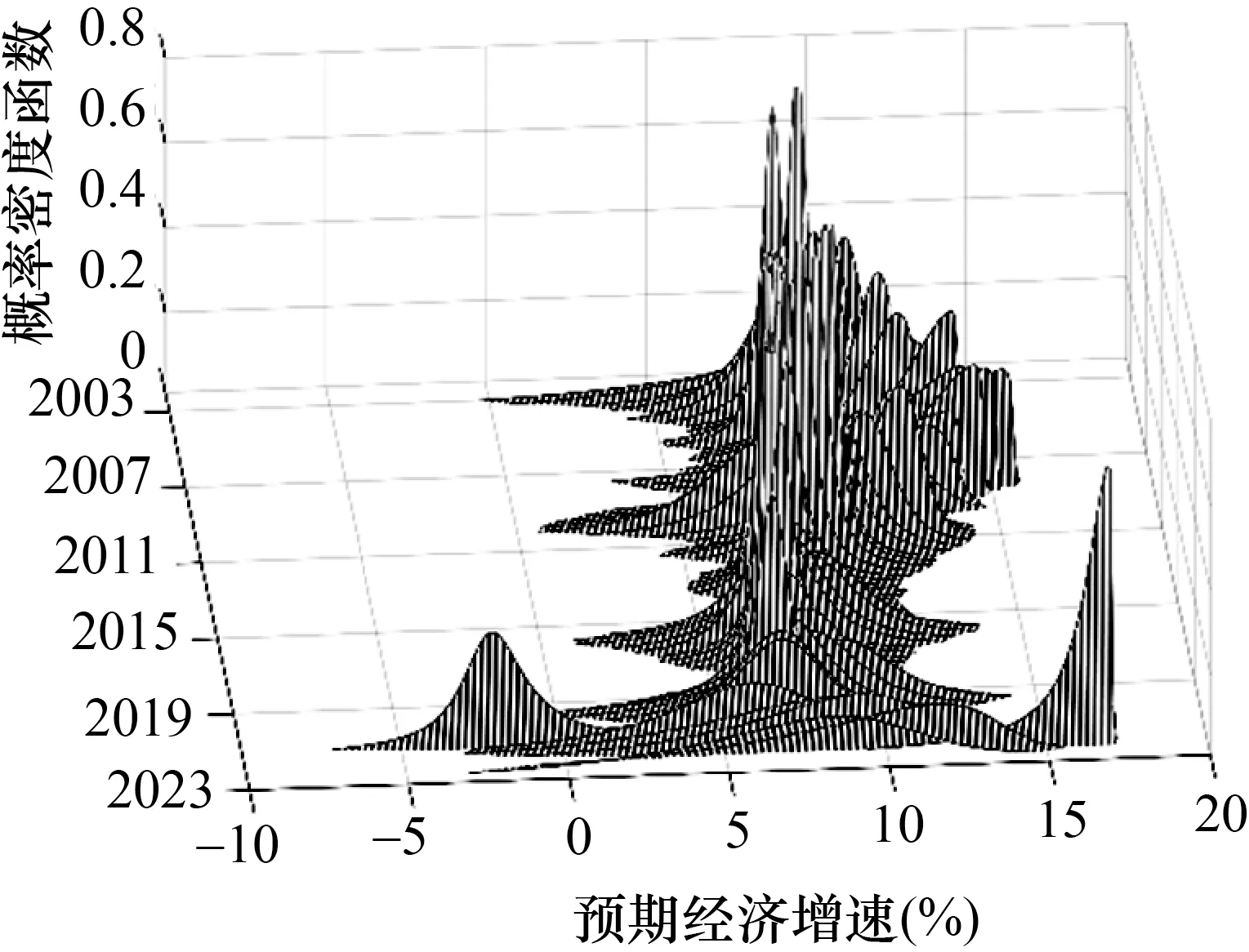
圖9 金融不確定性條件下預(yù)期經(jīng)濟增速分布

綜觀圖8 與圖9 能夠發(fā)現(xiàn)，經(jīng)濟不確定性與金融不確定性條件下的經(jīng)濟增速區(qū)間存在著明顯的共性特征。一方面，就時間變化趨勢而言，2002 年至2007 年期間，經(jīng)濟增速區(qū)間明顯右移；而在全球金融危機后，經(jīng)濟增速區(qū)間開始緩慢左移，這與中國過去二十年經(jīng)濟增長的階段轉(zhuǎn)換密切相關(guān)，也意味著中國經(jīng)濟已經(jīng)實現(xiàn)由高速增長階段轉(zhuǎn)向高質(zhì)量發(fā)展階段。另一方面，就不同時點上經(jīng)濟增速的區(qū)間特征而言，在不確定性較低的繁榮時期(例如2006 年、2012 年)，經(jīng)濟增速區(qū)間相對較短，經(jīng)濟預(yù)期較為確定；在不確定性較高的衰退時期(例如2008 年、2020 年)，經(jīng)濟增速區(qū)間明顯較長，經(jīng)濟預(yù)期存在較大的潛在波動空間。顯然，這從經(jīng)驗事實的視角進一步印證了不確定性對預(yù)期經(jīng)濟增速分布的沖擊存在非對稱性，表明前文的分位數(shù)回歸結(jié)果具有較強的穩(wěn)健性。事實上，分位數(shù)回歸的結(jié)果還表明，與金融不確定性相比較，經(jīng)濟不確定性蘊含更多引發(fā)經(jīng)濟增速變動的信息，能夠?qū)?jīng)濟增速產(chǎn)生更為強勁的驅(qū)動力。這也導(dǎo)致了圖8 與圖9 的顯著差異，即無論從經(jīng)濟增速的區(qū)間跨度抑或從概率分布的偏斜程度來看，基于經(jīng)濟不確定性條件的預(yù)期經(jīng)濟增速分布的波動都更為劇烈。

2.基于相對熵值和期望損失指標的中國經(jīng)濟風險確定性特征分析

本文運用偏態(tài)t分布擬合形成了具體的預(yù)期經(jīng)濟增速分布，其中預(yù)期經(jīng)濟增速分布即為分別考慮經(jīng)濟不確定性以及金融不確定性的條件經(jīng)濟增速分布。接下來，本文將從預(yù)期經(jīng)濟增速分布尾部區(qū)域的脆弱性(即不確定性)對預(yù)期經(jīng)濟增速分布尾部區(qū)域影響程度的視角出發(fā)，利用相對熵值和期望損失兩種指標，進一步量化經(jīng)濟上行風險與下行風險，從而印證不確定性對經(jīng)濟風險的非對稱影響，探析不確定性沖擊下經(jīng)濟風險的確定性特征。

相比于無條件經(jīng)濟增速分布，條件經(jīng)濟增速分布給右尾和左尾區(qū)域帶來的超額概率質(zhì)量能夠有效表征經(jīng)濟上行及下行風險。因此，本文采用gyt＋m表示無條件經(jīng)濟增速分布的概率密度函數(shù)，表示條件經(jīng)濟增速分布的概率密度函數(shù)，根據(jù)條件經(jīng)濟增速分布與無條件增速分布的尾部概率差異，將預(yù)期經(jīng)濟增速的上行熵值與下行熵值分別定義為與:

其中，是的累積分布函數(shù)，是條件經(jīng)濟增速分布的中位數(shù)。事實上，下行熵值衡量的是條件中位數(shù)以下條件概率和無條件概率的差異，因此當下行熵值較高時，條件經(jīng)濟增速分布的左尾區(qū)域相較于無條件增速分布具有更大概率，經(jīng)濟具有更高的下行風險。類似地，上行熵值衡量的是條件中位數(shù)以上條件概率和無條件概率的差異，因此當上行熵值較高時，條件經(jīng)濟增速分布的右尾區(qū)域相較于無條件增速分布具有更大概率，經(jīng)濟具有更高的上行風險。

此外，另一種衡量方法是利用期望損失(expected shortfall)模型測算條件經(jīng)濟增速分布尾部區(qū)域的平均經(jīng)濟增速，并以此量化經(jīng)濟上行及下行風險。其中，期望損失能夠有效測度經(jīng)濟的下行風險，而期望損失的上尾對應(yīng)值則可以清晰地展現(xiàn)經(jīng)濟的上行風險。具體地，對于一個給定的目標概率π，期望損失及其上尾對應(yīng)值可被分別定義為SFt＋m和LRt＋m:

事實上，IMF 明確提出將5%分位數(shù)的預(yù)期經(jīng)濟增速定義為在險經(jīng)濟增長率(以下簡稱“在險增長率”)，并以此衡量經(jīng)濟的下行風險(IMF，2017)。因此，在尾部風險的置信水平選擇上，為了與在險增長率的定義相匹配，本文將期望損失模型的目標概率設(shè)定為5%。此外，比較期望損失和相對熵值的定義能夠發(fā)現(xiàn)，盡管這兩種方式均衡量了預(yù)期經(jīng)濟增速的上行及下行風險，但是期望損失和相對熵值測度的信息含量明顯不同。其中，期望損失及其上尾對應(yīng)值僅從條件經(jīng)濟增速分布的視角刻畫了絕對尾部行為；而相對熵值則綜合考慮了條件和無條件兩種經(jīng)濟增速分布，描繪了條件經(jīng)濟增速分布與無條件經(jīng)濟增速分布的尾部概率差異，即相對尾部行為。

在描述了經(jīng)濟風險的衡量方法后，本文在圖10 中分別利用相對熵值和期望損失指標，清晰地量化了經(jīng)濟不確定性與金融不確定性條件下的經(jīng)濟上行及下行風險。其中，圖10(a)與圖10(b)描繪了預(yù)期經(jīng)濟增速上行熵值和下行熵值的動態(tài)軌跡，圖10(c)與圖10(d)刻畫了期望損失及其上尾對應(yīng)值的時變波動。綜觀圖10，盡管相對熵值和期望損失兩種指標在度量經(jīng)濟風險時存在一定的信息差異，但是卻展現(xiàn)出極為相似的預(yù)測結(jié)果。

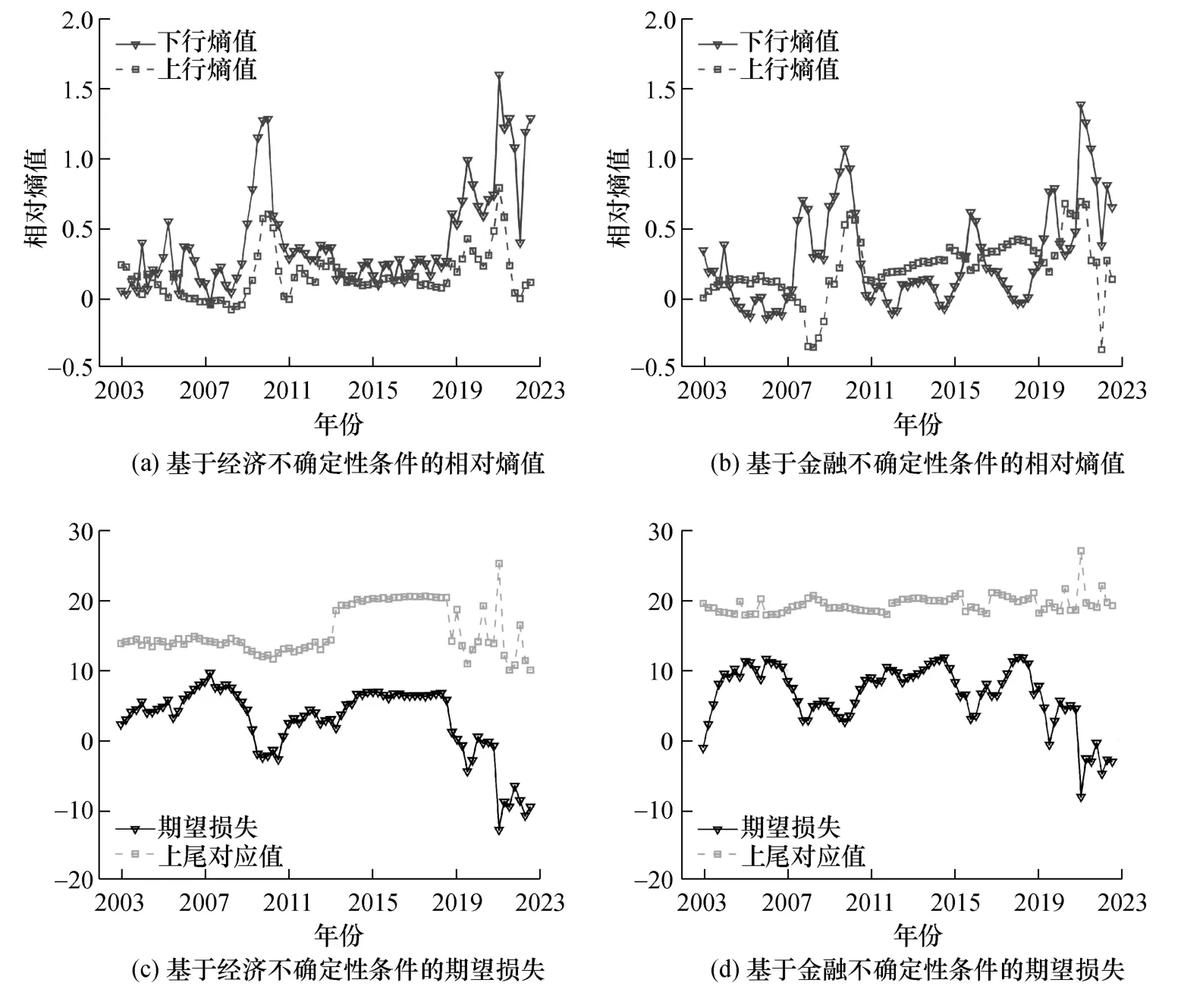
圖10 基于相對熵值和期望損失指標的經(jīng)濟風險走勢

一方面，觀察圖10(a)與圖10(b)不難看出，預(yù)期經(jīng)濟增速的上行熵值與下行熵值均呈現(xiàn)出明顯的波動態(tài)勢。其中，在全球金融危機以及新冠肺炎疫情期間(2008 年以及2020 年)，下行熵值大幅增加繼而顯著高于上行熵值。這表明，與無條件經(jīng)濟增速分布相比，預(yù)期經(jīng)濟增速分布的左尾具有更大的概率質(zhì)量，意味著不確定性沖擊使得經(jīng)濟具有更高的下行風險。這與前文強調(diào)的不確定性能夠造成非對稱影響的結(jié)論一致，進一步說明了不確定性沖擊中的確定性特征。需要注意的是，下行熵值在2010 年以后迅速降低，追根溯源，金融危機時期，為應(yīng)對經(jīng)濟增速快速回落以及出口負增長等嚴峻形勢，中國通過擴大政府投資和銀行信貸等方式，采取了一系列大規(guī)模的刺激政策，旨在保障經(jīng)濟平穩(wěn)較快增長，這些宏觀調(diào)控舉措使得預(yù)期經(jīng)濟增速的下行熵值顯著下降，最終接近于同期的上行熵值。類似地，2020 年后，伴隨著新冠肺炎疫情形勢的逐漸好轉(zhuǎn)，下行熵值同樣表現(xiàn)出快速下降的波動趨勢。這表明，中國經(jīng)濟具有較好的恢復(fù)能力，能夠從新冠肺炎疫情的泥淖中迅速復(fù)蘇，意味著中國具有較強的經(jīng)濟韌性與發(fā)展?jié)摿Α?/p>

另一方面，觀察圖10(c)與圖10(d)能夠發(fā)現(xiàn)，期望損失和上尾對應(yīng)值的波動路徑，與圖6 及圖7 中低分位數(shù)和高分位數(shù)預(yù)期經(jīng)濟增速的動態(tài)軌跡較為相似。具體而言，期望損失及其上尾對應(yīng)值同時呈現(xiàn)出明顯的波動態(tài)勢，但是，期望損失的波動顯然更為劇烈。例如，在全球金融危機、中美貿(mào)易摩擦以及新冠肺炎疫情等極端事件期間，期望損失表現(xiàn)出大幅下降的態(tài)勢，而上尾對應(yīng)值則僅有相應(yīng)的微幅震蕩。上述發(fā)現(xiàn)意味著，預(yù)期經(jīng)濟增速分布的尾部風險存在著顯著差異，與經(jīng)濟上行風險相比較，經(jīng)濟下行風險相對更大，波動也更為劇烈。因此，綜觀相對熵值與期望損失的模型測度結(jié)果能夠發(fā)現(xiàn)，不確定性沖擊對經(jīng)濟風險具有明顯的非對稱影響，伴隨著不確定性的升高，經(jīng)濟下行風險顯著增加，而經(jīng)濟上行風險則明顯較為穩(wěn)定。這與在險增長模型中低分位數(shù)和高分位數(shù)預(yù)期經(jīng)濟增速走勢的非對稱性特征相呼應(yīng)，繼而有效印證了不確定性沖擊下經(jīng)濟風險的確定性特征。

此外，綜觀圖10 能夠發(fā)現(xiàn)，無論是從相對熵值還是期望損失來看，經(jīng)濟不確定性均具有更為明顯的下行驅(qū)動作用。一方面，就相對熵值而言，在全球金融危機、中美貿(mào)易摩擦以及新冠肺炎疫情期間，基于經(jīng)濟不確定性條件的下行熵值的波峰始終相對更高。另一方面，就期望損失而言，在上述極端風險事件期間，基于經(jīng)濟不確定性條件的期望損失的波動幅度同樣更為劇烈，例如，新冠肺炎疫情時期，經(jīng)濟不確定性條件下的期望損失大幅降低(－13%)，而金融不確定性條件下的期望損失最終停留在相對較高的增速水平(－9%)。因此，本文從經(jīng)濟風險的多維度視角，進一步展示了經(jīng)濟不確定性與金融不確定性影響的異質(zhì)性。需要注意的是，觀察經(jīng)濟風險指標的時變走勢不難看出，盡管目前經(jīng)濟下行風險水平已從峰值回落，但中國仍處于不確定性較高的發(fā)展階段，潛存一定的經(jīng)濟下行風險。

五、中國經(jīng)濟風險的時變路徑識別與驅(qū)動機制分析

本文基于在險增長模型，描繪了預(yù)期經(jīng)濟增速的分布特征，刻畫了不確定性對經(jīng)濟風險的非對稱影響；隨后又利用相對熵值、期望損失等測度方法，進一步印證了不確定性沖擊下經(jīng)濟風險的確定性特征。然而，前文僅從經(jīng)濟風險的識別視角，揭示了不確定性視閾下經(jīng)濟風險的波動特征，并未對不確定性沖擊的動態(tài)影響進行深入探究。因此，為了實現(xiàn)不確定性沖擊下經(jīng)濟風險的時變路徑識別與驅(qū)動機制分析，本文將綜合考量經(jīng)驗證據(jù)和理論模型的預(yù)期結(jié)果，以期對不確定性的沖擊效應(yīng)進行系統(tǒng)性分析。

為了將經(jīng)驗證據(jù)與理論模型相匹配，我們選取季節(jié)調(diào)整后的實際GDP 季度值以及未經(jīng)過標準化處理的季度不確定性指數(shù)進行研究。需要說明的是，為了便于敏銳地捕捉不確定性對經(jīng)濟增速的動態(tài)影響，本文根據(jù)理論分析中預(yù)期經(jīng)濟增速的定義gt＋1＝lnyt＋1－lnyt，采用環(huán)比經(jīng)濟增速作為經(jīng)濟增速指標。具體地，本文首先計算實際GDP 季度值的迭代變化得到環(huán)比經(jīng)濟增速，隨后又對環(huán)比經(jīng)濟增速進行年化處理，最終采用年化環(huán)比經(jīng)濟增速指標展開進一步研究。①本部分的預(yù)期經(jīng)濟增速為采用實際GDP 季度值計算得到的季度年化環(huán)比增長率。

(一)不確定性的經(jīng)濟增長效應(yīng)分析

為了探究不確定性的經(jīng)濟增長效應(yīng)，驗證理論分析中不確定性對經(jīng)濟增速均值、波動率等分布特征的影響，本文分別在圖11 和圖12 中展示經(jīng)濟不確定性和金融不確定性與經(jīng)濟增速特征的相關(guān)性。其中，經(jīng)濟增速的分布特征由經(jīng)濟增長率及其高階矩構(gòu)成，具體以八期滾動窗測算的經(jīng)濟平均增速、經(jīng)濟增速波動率以及經(jīng)濟增速分布偏度三方面度量。

圖11 經(jīng)濟不確定性與經(jīng)濟增速特征的相關(guān)性

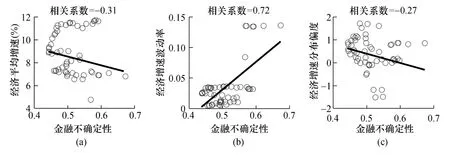
圖12 金融不確定性與經(jīng)濟增速特征的相關(guān)性

綜觀圖11 與圖12 不難看出，經(jīng)濟不確定性與金融不確定性對經(jīng)濟增速分布特征的影響較為一致。首先，觀察圖11(a)與圖12(a)可知，不確定性與經(jīng)濟平均增速呈現(xiàn)明顯的負相關(guān)關(guān)系。這是由于，無論是經(jīng)濟不確定性還是金融不確定性，在微觀層面均會影響居民的資產(chǎn)配置及企業(yè)投資，而在宏觀層面又會導(dǎo)致產(chǎn)出和消費的明顯下降，弱化宏觀經(jīng)濟政策的調(diào)控效果，即不確定性能夠引致經(jīng)濟活動減緩，從而使經(jīng)濟增長產(chǎn)生收縮效應(yīng)。其次，根據(jù)圖11(b)與圖12(b)可知，不確定性與經(jīng)濟增速波動率的相關(guān)系數(shù)顯著為正。事實上，不確定性的增加能夠?qū)е陆?jīng)濟增速分布的方差(即波動率)顯著上升，致使經(jīng)濟增速具有更大的波動空間，而經(jīng)濟增速的波動會再度反饋至不確定性，形成明顯的動態(tài)交互效應(yīng)，進而使得不確定性與增速波動率具有高度的相關(guān)性。最后，由圖11(c)與圖12(c)可知，不確定性與經(jīng)濟增速分布偏度具有負相關(guān)關(guān)系，表明不確定性會導(dǎo)致經(jīng)濟增長概率分布曲線趨于負向偏斜，從而引致更大的經(jīng)濟下行空間。有鑒于此，本文從經(jīng)驗證據(jù)的視角印證了理論分析中不確定性對經(jīng)濟增速相關(guān)特征的影響，即不確定性的增加會導(dǎo)致經(jīng)濟平均增速明顯下降，引發(fā)經(jīng)濟增速劇烈波動，并促使經(jīng)濟增長概率分布負向偏斜。

對比圖11 和圖12 所示的相關(guān)系數(shù)能夠發(fā)現(xiàn)，經(jīng)濟不確定性和金融不確定性與經(jīng)濟增速分布特征的相關(guān)性存在一定差異。其中，無論是就經(jīng)濟平均增速、經(jīng)濟增速波動率還是經(jīng)濟增速分布偏度而言，經(jīng)濟增速分布特征與經(jīng)濟不確定性的相關(guān)系數(shù)均明顯更大。這意味著，與金融不確定性相比，經(jīng)濟不確定性能夠引致更為顯著的經(jīng)濟下行風險。究其原因，金融不確定性作為經(jīng)濟景氣預(yù)測的先行指標，能夠更為靈敏地捕捉經(jīng)濟波動，而經(jīng)濟不確定性更多表現(xiàn)為宏觀經(jīng)濟波動的同步指標。因此，當經(jīng)濟不確定性顯著升高時，實體經(jīng)濟層面勢必呈現(xiàn)出明顯的實質(zhì)性波動，即經(jīng)濟不確定性對經(jīng)濟增速分布的影響相對更大。鑒于此，本文在印證理論分析中不確定性影響經(jīng)濟增長分布特征的同時，也進一步說明相較于金融不確定性，經(jīng)濟不確定性對于經(jīng)濟風險的影響更為顯著。

(二)不確定性對中國經(jīng)濟風險的時變沖擊路徑識別

在初步驗證不確定性的經(jīng)濟增長效應(yīng)后，本文將從理論分析與經(jīng)驗證據(jù)兩個視角刻畫不確定性對中國經(jīng)濟風險的時變沖擊路徑。其中，對于在險增長模型中的預(yù)期經(jīng)濟增速分布而言，不確定性對經(jīng)濟風險的沖擊路徑可以從以下兩個方面進行深入探討:一是不確定性對預(yù)期經(jīng)濟增速分布的時變沖擊效應(yīng)，二是不確定性對預(yù)期經(jīng)濟增速分布的實際沖擊效應(yīng)。

1.不確定性對預(yù)期經(jīng)濟增速分布的時變沖擊效應(yīng)分析

一方面，根據(jù)理論模型中的構(gòu)造，σ2為刻畫不確定性的唯一參數(shù)。因此，為便于計算不確定性對預(yù)期經(jīng)濟增速分布的沖擊效應(yīng)，本文首先設(shè)定σ＝1。現(xiàn)有文獻中的常見取值，如王立勇和徐曉莉(2018)，將中國的效用貼現(xiàn)率β設(shè)為0.98。接下來，根據(jù)式(12)，改變σ值使得不確定性τ增加10%①根據(jù)不確定性指數(shù)的實際數(shù)據(jù)，不確定性增加1 單位標準偏差沖擊對應(yīng)于不確定性τ 增加10%。，以期得到不確定性對預(yù)期經(jīng)濟增速分布沖擊的理論預(yù)期結(jié)果。另一方面，利用不確定性指數(shù)與經(jīng)濟增速數(shù)據(jù)，可以構(gòu)建如式(31)所示的條件分位數(shù)回歸模型。需要說明的是，本文根據(jù)Jorda(2005)的局部投影估計方法，利用不同預(yù)測期m＝1，2，…，12 (季度)回歸系數(shù)的變化路徑，表征不確定性沖擊對預(yù)期經(jīng)濟增速的動態(tài)影響。在此基礎(chǔ)上，給定經(jīng)濟不確定性與金融不確定性1 單位標準差沖擊，即可得到不同分位數(shù)預(yù)期經(jīng)濟增速的脈沖響應(yīng)。因此，本文在圖13 中描繪出不確定性對預(yù)期經(jīng)濟增速分布的沖擊路徑。其中，圖13(a)展示了理論模型預(yù)期的脈沖響應(yīng)結(jié)果，圖13(b)與圖13(c)則分別刻畫了經(jīng)濟不確定性與金融不確定性沖擊的脈沖響應(yīng)結(jié)果。

圖13 預(yù)期經(jīng)濟增速分布對不確定性沖擊的脈沖響應(yīng)軌跡

圖13 中理論分析與經(jīng)驗證據(jù)的結(jié)果一致表明，不確定性對低分位數(shù)與高分位數(shù)預(yù)期經(jīng)濟增速的沖擊具有明顯的非對稱性，這與前文的研究結(jié)論完全相符。具體地，就理論模型的預(yù)期結(jié)果圖13(a)而言，不確定性沖擊增加1 單位，會立刻引致預(yù)期經(jīng)濟增速的5%分位數(shù)下降3%，95%分位數(shù)上漲2%；就經(jīng)驗證據(jù)圖13(b)與圖13(c)而言，經(jīng)濟不確定性與金融不確定性沖擊增加1 單位，會立刻引致預(yù)期經(jīng)濟增速的5%分位數(shù)下降5%，95%分位數(shù)上漲2%。這意味著，不確定性沖擊會迅速使得未來經(jīng)濟增速的下限值大幅度下降，經(jīng)濟增速上限值小幅度上升，從而顯著增加經(jīng)濟下行風險，同時較小地增加經(jīng)濟上行風險。

比較圖13(b)與圖13(c)中的脈沖響應(yīng)軌跡不難發(fā)現(xiàn)，經(jīng)濟不確定性與金融不確定性的沖擊效應(yīng)存在著明顯差異。一方面，從沖擊效應(yīng)的持續(xù)時間來看，經(jīng)濟不確定性的影響周期相對更長。其中，經(jīng)濟不確定性對低分位數(shù)預(yù)期經(jīng)濟增速的影響存在一定的滯后效應(yīng)，致使低分位數(shù)預(yù)期經(jīng)濟增速于第2 期實現(xiàn)最大負向響應(yīng)。然而，金融不確定性對低分位數(shù)預(yù)期經(jīng)濟增速的沖擊則在第1 期達到峰值，隨后，脈沖響應(yīng)軌跡呈現(xiàn)穩(wěn)定的收斂趨勢。另一方面，從沖擊效應(yīng)的影響程度來看，盡管低分位數(shù)預(yù)期經(jīng)濟增速對兩種不確定性沖擊的脈沖響應(yīng)在第12 期均為－1%，但是經(jīng)濟不確定性對5%分位數(shù)預(yù)期經(jīng)濟增速的最大沖擊接近－6%，而同期(第2 期)金融不確定性沖擊僅為－3%，意味著經(jīng)濟不確定性具有更大的下行驅(qū)動力。

綜上所述，理論模型的預(yù)期結(jié)果與實際沖擊的時變路徑在總體上較為相似，表明不確定性沖擊下經(jīng)濟風險具有確定性響應(yīng)路徑的同時，也進一步印證了理論分析框架的合理性。根據(jù)預(yù)期經(jīng)濟增速分布的脈沖軌跡，相比于金融不確定性，經(jīng)濟不確定性沖擊不僅持續(xù)時間更久，而且影響程度更大，能夠引致更大的經(jīng)濟下行風險。此外，理論分析與經(jīng)驗證據(jù)的結(jié)果還表明，不確定性的沖擊效應(yīng)隨著時間的推移逐漸收斂。這意味著，即使沒有外生宏觀調(diào)控政策的對沖，不確定性沖擊的負面影響也會逐漸減弱，體現(xiàn)了經(jīng)濟具有恢復(fù)增長的內(nèi)在韌性。但是，12 期(三年)后的沖擊效應(yīng)仍未減弱至零，表明不確定性沖擊需要較長的消化周期，能夠?qū)?jīng)濟增長產(chǎn)生長遠的負向影響。

2.不確定性對預(yù)期經(jīng)濟增速分布的實際沖擊效應(yīng)檢驗

為了深入探究不確定性對經(jīng)濟風險的實際沖擊效應(yīng)，本文基于預(yù)期經(jīng)濟增速分布特征中分散程度以及在險增長率(5%分位數(shù)的預(yù)期經(jīng)濟增速)的脈沖響應(yīng)軌跡，揭示不確定性沖擊對未來經(jīng)濟增速的區(qū)間范圍以及經(jīng)濟下行風險的時變影響。進一步地，為了模擬更大規(guī)模不確定性沖擊的預(yù)期影響，本文再度調(diào)整理論模型中的參數(shù)σ，使得不確定性水平增加20%，繼而實現(xiàn)不同規(guī)模理論沖擊與實證沖擊的對比分析，刻畫不確定性的實際沖擊效應(yīng)。圖14 展示了預(yù)期經(jīng)濟增速分布對不同規(guī)模不確定性沖擊的脈沖響應(yīng)結(jié)果。其中，圖14 (a)與圖14 (c)描繪了不確定性對預(yù)期經(jīng)濟增速分布分散程度的沖擊效應(yīng)，圖14 (b)與圖14 (d)則刻畫了不確定性對在險增長率的沖擊效應(yīng)，虛線表示經(jīng)濟不確定性或金融不確定性增加1 單位標準差沖擊后產(chǎn)生的脈沖響應(yīng)軌跡。需要說明的是，分散程度利用預(yù)期經(jīng)濟增速分布的上4 分位數(shù)(75%分位數(shù))與下4 分位數(shù)(25%分位數(shù))之差，即4 分位距予以衡量。4 分位距將預(yù)期經(jīng)濟增速分布的尾部風險值排除在外，能夠在反映未來經(jīng)濟增速區(qū)間主體范圍的同時，更清晰地展現(xiàn)經(jīng)濟增長“期望值”(即未來經(jīng)濟增速預(yù)測值)的運行區(qū)間。

圖14 預(yù)期經(jīng)濟增速分布對不同規(guī)模不確定性沖擊的脈沖響應(yīng)

一方面，就圖14 中理論模型的預(yù)期結(jié)果而言，不確定性增加10%會立刻導(dǎo)致預(yù)期經(jīng)濟增速分布的分散程度增加2%，在險增長率下降4%；而不確定性增加20%則會引致分散程度增加4%，在險增長率降低6%。另一方面，就圖14 中的實證結(jié)果而言，1 單位經(jīng)濟不確定性與金融不確定性沖擊能夠使得分散程度立刻增加2.5%，在險增長率下降5%。因此，結(jié)合圖13 中不同分位數(shù)預(yù)期經(jīng)濟增速對不確定性沖擊的脈沖響應(yīng)軌跡可以判斷，不確定性沖擊能夠引致未來經(jīng)濟增速的運行區(qū)間范圍迅速擴張。其中，區(qū)間上限會小幅下降，而區(qū)間下限會大幅降低，這意味著不確定性在驅(qū)動經(jīng)濟下行的同時也顯著擴大了經(jīng)濟增速的下行空間。

此外，無論是從預(yù)期經(jīng)濟增速分布分散程度還是在險增長率的脈沖響應(yīng)來看，經(jīng)濟不確定性造成的沖擊效應(yīng)都更為劇烈，十分接近大規(guī)模沖擊的影響程度。具體而言，觀察圖14(a)與圖14(c)可知，經(jīng)濟不確定性對分散程度的沖擊效應(yīng)在前兩期相等且最大，隨后呈現(xiàn)出緩慢的波浪式下降趨勢。但是，第7 期后的沖擊不再減弱，始終停留在1.5%的水平附近；金融不確定性對分散程度的沖擊在第1 期實現(xiàn)最大值后隨即收斂，最終減弱至零。這意味著，經(jīng)濟不確定性能夠?qū)ξ磥斫?jīng)濟增速造成一定規(guī)模的永久性沖擊，即1 單位經(jīng)濟不確定性沖擊會使得經(jīng)濟增速的區(qū)間范圍擴大1.5%，這也印證了基于經(jīng)濟不確定性條件的預(yù)期經(jīng)濟增速更為分散的分布特征。類似地，比較圖14(b)與圖14(d)可以發(fā)現(xiàn)，經(jīng)濟不確定性對在險增長率的沖擊效應(yīng)始終圍繞在大規(guī)模沖擊附近，而金融不確定性對在險增長率的影響相對較小且衰減較快。因此，本文從預(yù)期經(jīng)濟增速分布特征的視角，進一步說明了經(jīng)濟不確定性沖擊的影響程度更大、持續(xù)時間更久。

需要注意的是，比較圖14 中實證數(shù)據(jù)與理論模擬的脈沖結(jié)果不難發(fā)現(xiàn)，無論是就經(jīng)濟不確定性還是金融不確定性而言，不確定性的實際沖擊效應(yīng)均介于理論模型預(yù)期的小規(guī)模沖擊與大規(guī)模沖擊之間。這意味著，不確定性對預(yù)期經(jīng)濟增速的實際影響明顯大于理論分析中同等規(guī)模的沖擊效應(yīng)。究其原因，相比于理論模型擬合的預(yù)期沖擊，不確定性除了能夠通過產(chǎn)生恐慌情緒等難以量化的微觀渠道放大其實際沖擊效應(yīng)，更為重要的是，在不確定性降低經(jīng)濟增速的同時，經(jīng)濟增速的下降還會引致不確定性水平的進一步增加，即不確定性對經(jīng)濟增長的影響存在“雙向反饋” 的動態(tài)溢出循環(huán)。這使得不確定性沖擊在現(xiàn)實情境下表現(xiàn)出更為復(fù)雜的經(jīng)濟效應(yīng)，能夠加劇不確定性對經(jīng)濟風險的實際沖擊作用。

(三)基于理論框架的中國經(jīng)濟風險驅(qū)動機制分析

本文通過綜合分析理論模型預(yù)期與實證檢驗的脈沖響應(yīng)結(jié)果，有效揭示了不確定性沖擊下經(jīng)濟風險具有確定性的時變響應(yīng)路徑，驗證了理論模型構(gòu)建的合理性。然而，這也衍生出一系列問題:何為“技能缺口”? 為何“技能缺口” 的波動能夠定義不確定性?不確定性又如何驅(qū)動經(jīng)濟風險?

所謂技能缺口，其在理論模型中等價于企業(yè)現(xiàn)有技能組合與最優(yōu)技能組合之差，而在本質(zhì)上反映的是經(jīng)濟投入要素(包括勞動和資本投入)無法滿足企業(yè)技術(shù)要求的比例。不難發(fā)現(xiàn)，技能缺口充分體現(xiàn)了企業(yè)技術(shù)水平與投入要素之間的矛盾關(guān)系，技能缺口越大，表明企業(yè)的技術(shù)水平與投入要素越不匹配。從企業(yè)的實際生產(chǎn)經(jīng)營決策來看，技術(shù)水平以及投入要素的動態(tài)調(diào)整，正是企業(yè)應(yīng)對外部環(huán)境不確定的內(nèi)在表現(xiàn)，因此本文利用技能缺口的波動刻畫不確定性。事實上，企業(yè)動態(tài)調(diào)整技術(shù)以及投入要素這一過程，能夠根據(jù)企業(yè)實際產(chǎn)出與潛在產(chǎn)出的比例波動進行清晰刻畫。而在實踐中，產(chǎn)能利用率作為總產(chǎn)出對生產(chǎn)設(shè)備的比率，可以有效地反映實際產(chǎn)出對潛在產(chǎn)出的比例。有鑒于此，本文將產(chǎn)能利用率與技能缺口聯(lián)系起來，利用產(chǎn)能利用率的波動對不確定性的概念進行量化，繼而從實際生產(chǎn)的視角闡釋不確定性的經(jīng)濟含義，分析理論框架中不確定性對經(jīng)濟風險的驅(qū)動機制。

圖15 展示了產(chǎn)能利用率波動與經(jīng)濟下行風險的相關(guān)性。其中，圖15(a)描繪了產(chǎn)能利用率波動與經(jīng)濟不確定性條件下在險增長率的相關(guān)性，圖15(b)則刻畫了產(chǎn)能利用率波動與金融不確定性條件下在險增長率的相關(guān)性。不難發(fā)現(xiàn)，產(chǎn)能利用率波動與在險增長率呈現(xiàn)出明顯的負相關(guān)關(guān)系。究其原因，當經(jīng)濟景氣繁榮時，廠商往往過度樂觀，盈利能力的提高會強化其對未來看好的預(yù)期，廠商會擴大投資并提高產(chǎn)能利用率；一旦經(jīng)濟景氣發(fā)生逆轉(zhuǎn)，市場需求會迅速下降，此時產(chǎn)能過剩不可避免，進而經(jīng)濟主體產(chǎn)能利用率降低，這在一定程度上會加劇經(jīng)濟波動。因此，產(chǎn)能利用率的大幅波動意味著外部環(huán)境具有強烈的不確定性，故與更大的經(jīng)濟下行風險密切相關(guān)。

圖15 產(chǎn)能利用率波動與經(jīng)濟下行風險的相關(guān)性

此外，比較圖15(a)與圖15(b)可知，與金融不確定性條件下的在險增長率相比，產(chǎn)能利用率波動與經(jīng)濟不確定性條件下的在險增長率相關(guān)系數(shù)明顯更大。追根溯源，產(chǎn)能利用率作為衡量生產(chǎn)部門尤其是第二產(chǎn)業(yè)生產(chǎn)經(jīng)營狀況的重要指標，與基于實體經(jīng)濟層面的經(jīng)濟不確定性關(guān)系更為密切，而與金融市場的不確定性關(guān)聯(lián)程度則相對較小。因此，產(chǎn)能利用率波動與經(jīng)濟不確定性引致的下行風險相關(guān)性更為顯著。本文基于產(chǎn)能利用率的視角，運用實際數(shù)據(jù)刻畫了理論框架中技能缺口的概念，繼而在分析產(chǎn)能利用率波動與經(jīng)濟下行風險相關(guān)性的同時，闡釋了內(nèi)生不確定性的經(jīng)濟含義，進而有效印證了技能缺口—內(nèi)生不確定性—經(jīng)濟風險的驅(qū)動機制。

六、結(jié)論與政策啟示

首先，本文利用高維因子模型，實現(xiàn)經(jīng)濟不確定性與金融不確定性的分離測度。其次，基于經(jīng)濟增長概率分布的視角，本文將經(jīng)濟增長與不確定性納入在險增長的統(tǒng)一框架，繼而識別不確定性視閾下經(jīng)濟風險的確定性特征。最后，本文綜合考量經(jīng)驗證據(jù)與理論模型的預(yù)期結(jié)果，實現(xiàn)不確定性沖擊下經(jīng)濟風險的時變路徑識別與驅(qū)動機制分析。本文得出如下結(jié)論。第一，預(yù)期經(jīng)濟增速的條件分位數(shù)回歸結(jié)果表明，不確定性對經(jīng)濟風險具有明顯的非對稱影響。相比于經(jīng)濟上行風險，不確定性對經(jīng)濟下行風險具有更為顯著的影響，從而能夠引致更大的經(jīng)濟下行風險。隨后，基于在險增長、相對熵值以及期望損失等模型的測度結(jié)果，有效印證不確定性對經(jīng)濟風險的非對稱影響，進一步揭示不確定性沖擊下經(jīng)濟風險的確定性特征，即伴隨著不確定性的升高，經(jīng)濟下行風險顯著增加，而經(jīng)濟上行風險則較為穩(wěn)定，并且當經(jīng)濟處于不確定性較高的風險階段時，這種非對稱性特征會更加明顯。第二，預(yù)期經(jīng)濟增速分布的時變路徑表明:一方面，就預(yù)期經(jīng)濟增速的變化趨勢而言，2002 年至2007 年間，經(jīng)濟增速持續(xù)升高，而在全球金融危機后，經(jīng)濟增速開始逐漸放緩，證實中國經(jīng)濟已經(jīng)實現(xiàn)由高速增長階段轉(zhuǎn)向高質(zhì)量發(fā)展階段。另一方面，就預(yù)期經(jīng)濟增速的區(qū)間特征而言，當不確定性較低時，未來經(jīng)濟增速的潛在波動空間相對較小，經(jīng)濟預(yù)期較為明確；而當不確定性較高時，未來經(jīng)濟增速通常具有較大的波動空間。這意味著，不確定性沖擊不僅能夠引致經(jīng)濟增速大幅下降，而且會致使經(jīng)濟增速下行空間顯著擴張。第三，從不確定性的時變沖擊路徑來看，不確定性沖擊下的預(yù)期經(jīng)濟增速分布呈現(xiàn)出非對稱性的脈沖響應(yīng)軌跡，并且不確定性沖擊的消化周期相對較長，能夠?qū)?jīng)濟增長產(chǎn)生長遠的負向影響。從不確定性的實際沖擊效應(yīng)來看，經(jīng)驗證據(jù)與理論分析的預(yù)期結(jié)果表明，不確定性對經(jīng)濟增長的實際影響明顯大于理論分析中同等規(guī)模沖擊的沖擊效應(yīng)。這意味著，不確定性對經(jīng)濟增長的影響具有“雙向反饋” 的動態(tài)溢出循環(huán)，使得不確定性在現(xiàn)實情境下表現(xiàn)出更為復(fù)雜的經(jīng)濟效應(yīng)，能夠加劇不確定性對經(jīng)濟風險的實際沖擊作用。第四，根據(jù)預(yù)期經(jīng)濟增速的條件分位數(shù)回歸結(jié)果、經(jīng)濟風險的測度指標以及不確定性沖擊的脈沖響應(yīng)軌跡等一系列經(jīng)驗證據(jù)，經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險具有明顯的異質(zhì)性影響。其中，無論是就不確定性沖擊的影響程度還是持續(xù)周期而言，經(jīng)濟不確定性的影響均更為顯著。這意味著，與金融不確定性相比較，經(jīng)濟不確定性包含更多引發(fā)經(jīng)濟增速波動的信息，能夠引致更大的經(jīng)濟下行風險，致使經(jīng)濟表現(xiàn)出悲觀的增速預(yù)期。

基于上述結(jié)論，本文提出如下政策建議:第一，要充分認識不確定性沖擊中的確定性規(guī)律，重視不確定性對經(jīng)濟風險的非對稱沖擊效應(yīng)，選擇更具針對性的監(jiān)管目標和政策工具。當不確定性水平較高時，不僅應(yīng)當關(guān)注未來經(jīng)濟增長的預(yù)期值，更要重點監(jiān)控和防范不確定性沖擊引致的巨大經(jīng)濟下行風險，進一步強化風險監(jiān)管與預(yù)期管理，保障經(jīng)濟運行在合理區(qū)間。第二，要創(chuàng)新與優(yōu)化宏觀經(jīng)濟調(diào)控，將在險增長、相對熵值、期望損失等參考指標納入宏觀調(diào)控范疇，健全風險監(jiān)測預(yù)警和早期干預(yù)機制，加強宏觀經(jīng)濟政策與審慎監(jiān)管措施的協(xié)調(diào)配合。第三，在應(yīng)對不確定性沖擊的負面影響時，要加強與經(jīng)濟主體的溝通交流，引入前瞻性指引等政策工具，強化公眾的預(yù)期管理，避免產(chǎn)生夸大“壞消息”、忽視“好消息” 的市場恐慌情緒。同時，要積極制定和實施宏觀調(diào)控政策，提高宏觀調(diào)控有效性，優(yōu)化完善沖擊處理機制，主動防范和化解由不確定性的內(nèi)生放大機制形成的疊加沖擊。第四，考慮到經(jīng)濟不確定性與金融不確定性的同期水平存在顯著差異，并且經(jīng)濟不確定性與金融不確定性對經(jīng)濟風險具有明顯的異質(zhì)性影響，監(jiān)管當局應(yīng)密切關(guān)注經(jīng)濟和金融狀況及其不確定性因素，充分意識到金融不確定性的先導(dǎo)性特征，重點關(guān)注經(jīng)濟不確定性的劇烈變化，在努力實現(xiàn)“穩(wěn)增長” 與“防風險” 雙重目標的背景下，為經(jīng)濟平穩(wěn)健康發(fā)展營造良好的外部環(huán)境。

目前，中國正處于全面貫徹黨的二十大精神的關(guān)鍵之年，在這重要的歷史節(jié)點上，面對紛繁復(fù)雜的外部環(huán)境，國內(nèi)經(jīng)濟“穩(wěn)增長” 承受著空前壓力。在此背景下，識別不確定性與經(jīng)濟風險之間的關(guān)系，揭示不確定性中的確定性規(guī)律，對于國民經(jīng)濟健康發(fā)展至關(guān)重要。唯有強化風險監(jiān)管與預(yù)期管理，創(chuàng)新宏觀經(jīng)濟調(diào)控體系，方能防范化解經(jīng)濟金融風險，保持經(jīng)濟運行在合理區(qū)間，進而有利于加快構(gòu)建新發(fā)展格局，實現(xiàn)第二個百年奮斗目標，以中國式現(xiàn)代化全面推進中華民族偉大復(fù)興。