土壤中有機質鎘的同位素組成特征:來自第一性原理計算的約束

張田迪,邢樂才,2,趙浩男,李 英,谷一帆,楊 陽,何洪濤,2*

(1.河北工程大學 地球科學與工程學院,河北 邯鄲 056038;2.河北工程大學 河北省資源調查與研究重點實驗室,河北 邯鄲 056038)

鎘(Cd)是銀白色帶藍色光澤的金屬元素,位于周期表的第五周期第二副族中。它的偶次原子結構決定了它易失掉最外層電子,成為對稱結構的鈀型穩定離子[1]。因此,在表生環境下Cd主要以+2價形式存在。重金屬Cd主要通過鉛鋅礦石的開采和冶煉、工業制造和濫用化學肥料等人為活動排放到土壤中,已成為全球土壤主要重金屬污染物之一[2]。大多數地質及環境樣品中Cd含量極低,痕量、超痕量Cd元素含量的準確測定及高精度的同位素分析仍是一項具有挑戰性的研究工作[3]。然而,當環境中的某些物理化學過程能夠導致較大的金屬同位素分餾時,示蹤工作變得復雜,需要識別和量化單個過程中的同位素分餾程度。例如,有機質表面吸附及螯合過程在表生條件下普遍存在,是影響Cd同位素分餾的重要過程,但該過程中的同位素分餾尚未得到有效的限定。有機質作為土壤的重要組成部分,占土壤固體部分的5%。而有機質中85%是腐殖質。腐殖質作為環境中許多必需和有毒微量元素的吸附劑,在控制其在土壤、沉積物和水生系統中的流動性和生物有效性中發揮著重要的作用[4]。

確定分餾特征(程度)的方法主要有三種,分別是理論計算、實驗測定、野外半定量評估[5]。迄今為止,只有少數實驗室對吸附和絡合過程中鎘同位素分餾進行了量化[6]。然而,同位素交換平衡所需的時間尺度不同于元素平衡,很難判斷同位素交換反應是否達到真正意義上的平衡。因此,將實驗結果外推到自然條件時必須謹慎。如今,基于密度泛函數理論(DFT)的第一性原理計算方法已成為實驗研究的重要補充[7]。它可以提供同位素交換反應中關鍵步驟的詳細信息。該技術的主要原理是分子的各種熱力學性質(反應吉布斯自由能變化、IR活性、化學位移等)與其電子密度具有緊密的函數關系。通過求解分子的Schr?dinger方程,可以得到對應于最穩定的化學結構的電子能和體系波函數。作為同位素分餾因子計算中的關鍵參數,諧波振動頻率即為電子能對原子坐標的二階偏導。

1 理論與方法

本研究采用第一性原理計算方法對分子團簇進行幾何構型優化。使用BP86作為交換相關函數,采用混合基組描述體系的波函數,即Cd選擇LanL2MB贗勢基組[8],H,O,N, 和 S原子選擇6-311G(d)全電子基組[9]。幾何優化完成后,我們檢查每一組構型的諧振動頻率中是否存在虛頻,以確認該構型是否對應勢能面上的局部極小值。體系電子能和諧振動頻率計算均通過Gaussian09/ Gaussian16軟件[10-11]完成。

1.1 平衡分餾系數計算

Urey 等[12-13]描述了化合物和單原子理想氣體之間同位素交換的場景。他們提出了一個重要的參數,即約化配分函數(Reduced Partition Function Ratio, RPFR),來量化化合物相對富集重同位素的程度。該參數值大小主要取決于同位素替換前后的化合物的諧振動頻率。RPFR值越大于1,表明該物質中的重同位素富集程度越大。

對于化合物和單原子理想氣體之間的同位素交換反應:

AX+X'AX'+X

(1)

式中,X'代表含有重同位素的單原子理想氣體,X代表含有輕同位素的單原子理想氣體,AX代表具有輕同位素的化合物,AX'代表具有重同位素的化合物。該反應的平衡常數可表示為

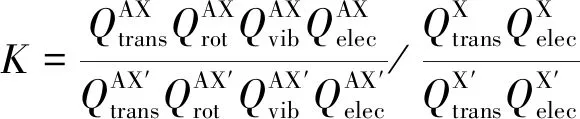
(2)

其中Qtrans、Qrot、Qvib、Qelec分別表示平動配分函數、轉動配分函數、振動配分函數、電子配分函數。對于輕元素來說,同位素替換前后的化合物的基態電子能差異基本上是無法區分的,因此可以忽略電子配分函數對RPFR值的貢獻。具體而言,平動配分函數、轉動配分函數和振動配分函數可以表示成:

(3)

(4)

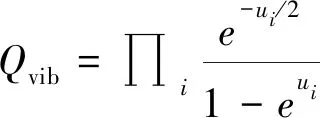
(5)

其中V是分子體積,M是分子質量,IA是轉動軸A的轉動慣量,σ是分子的對稱數。ui=hcωi/kT,h為普朗克常數,k為玻爾茲曼常數,T為絕對溫度(K),c是光速,ω為諧振動頻率(cm-1)。使用Teller-Redlich[14]公式進一步近似,可以得到:

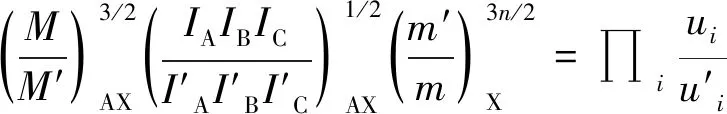
(6)

最終,平動配分函數比和轉動配分函數比可以使用振動頻率來表示。通過一系列數學變換,約化配分函數比(RPFR(AX/AX’))定義如下:

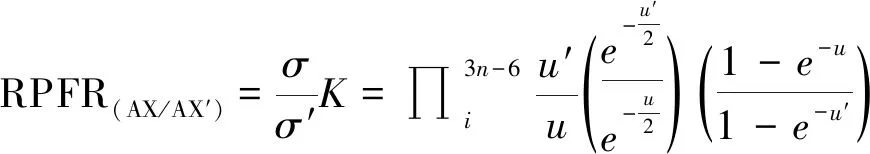
(7)

RPFR值等價于化學領域常用的β因子,即化合物與單原子理想氣體的同位素分餾因子[15]。當平衡共存的A、B兩相的RPFR已知時,則同位素分餾系數α可以由它們的RPFR(或β因子)的比值來表示:

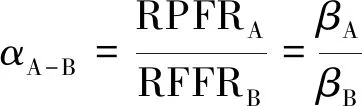
(8)

兩相之間的同位素平衡分餾值由公式:ΔA-B=δA-δB≈1 000(lnβA-lnβB)=1 000lnαA-B計算得到。該公式將同位素理論計算與實驗測定工作聯系起來,便于同位素分餾數據的對比。

同時,本文利用最小均方根偏差法[16]來確定每個含Cd物種RPFR值的平臺值:

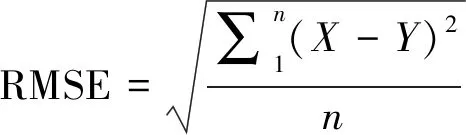
(9)

其中X代表我們計算出的每一個RPFR值,Y為預期的平臺值。RMSE值隨Y值的變化而變化,RMSE值取得最小值時對應的Y值,即為某含Cd物種的平臺值。

1.2 分子簇模型構建

腐殖酸的具體結構尚不清楚且分子量較大,其復雜程度超過了現階段的計算模擬能力,但是已知腐殖酸的各吸附點位上能夠絡合金屬離子的結構主要為含氧官能團,如羧基和酚羥基等。因此,我們使用小分子有機酸來代替腐殖酸,以此構建OSCs和MOFs的初始構型。OSCs初始構型優化結束后,在優化好的構型上繼續添加水分子,搭建下一組吸附態的初始構型。每次加6～7個水分子,建立下一組吸附Cd的初始構型。添加的水分子放置在氫鍵的成鍵范圍內(1.8～2.1 ?),并且使水分子中的氧原子(或者氫原子)盡可能與其他水分子的氫原子(或者氧原子)形成氫鍵。每完成一組構型優化,提取諧振動頻率,計算RPFR值。隨著添加水分子數量的增加,RPFR值逐漸收斂于平臺值。同時,腐殖酸中的N、S也可作為供體原子與金屬絡合。根據CCDC晶體數據庫中心提供的構型數據,對其構型進行修改來構建MOFs構型。OSCs和MOFs之間的區別在于,OSCs構型模擬Cd吸附在有機質表面,周圍有較多的水分子,而MOFs構型模擬Cd脫水進入有機質內部,配體中無水或水分子較少。在MOFs構型中我們還考慮了具有羥基、羧基、N原子和S原子不同組合的有機配體情形。

2 結果與討論

2.1 OSCs和MOFs的幾何構型

優化完成的OSCs和MOFs構型見圖1。同位素平衡分餾主要受到局部結構的控制[17],一般為距離目標原子3～5 ?范圍內的化學作用。因此,對Cd原子周圍化學環境模擬的準確性主要決定了同位素分餾系數計算的準確性。從圖1、圖2中,可以看出OSCs和MOFs均保留住了Cd-O八面體的初始構型。在OSCs中Cd-O平均鍵長為2.33 ?,在MOFs中Cd-O平均鍵長為2.40 ?。同時,Cd與N或S配位,將會增大Cd與第一配位層的原子間距。計算的Cd-O鍵長與公開發表的數據(表1)吻合較好,在一定程度上保證了1 000 lnβ的正確性。

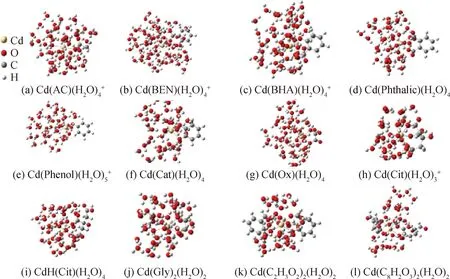
圖1 Cd OSCs幾何構型

表1 含Cd 物種與水溶液之間的平衡同位素分餾

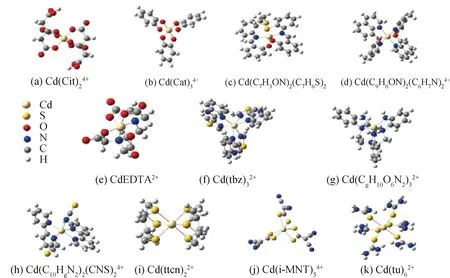
圖2 Cd MOFs幾何構型

2.2 同位素平衡分餾

基于水溶液的RPFR值(1.002 887)[7],計算出25 ℃下OSCs和MOFs與水溶液之間的Cd同位素平衡分餾值(圖3)。發現,OSCs溶劑效應模擬的準確性直接影響到Cd同位素平衡分餾值的選取。隨著水化層中水分子數的逐漸增加,分餾值由波動狀態逐漸收斂,直到達到平臺值。

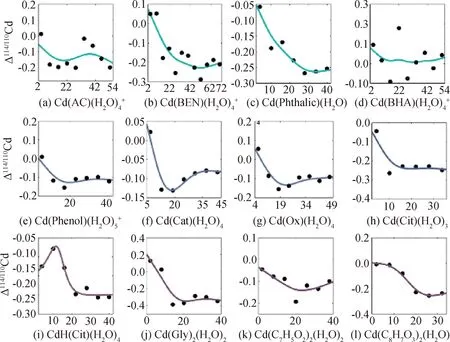
圖3 溶劑效應對OSCs與溶液間Cd同位素分餾的影響

最終,獲得了OCSs與溶液之間的Cd同位素平衡分餾為-0.34‰～0.02‰,最大值為0.02‰,最小值為-0.34‰,平均值為-0.17‰。同樣地,我們獲得了MOFs與溶液之間的Cd同位素平衡分餾為-1.92‰～-0.29‰,最大值為-0.29‰,最小值為-1.92‰,平均值為-0.87‰。明顯地,當Cd與N或S配位,同位素分餾更為顯著。

計算結果與土壤剖面的測試結果是一致的(圖3)。由于土壤礦物表面吸附過程產生的Cd同位素分餾在分餾方向和分餾程度上與有機質表面吸附過程相當,其中鐵(氫氧)氧化物分餾值為(-0.53±0.04)‰[25],錳氫氧化物分餾值為(-0.24±0.12)‰～(-0.54±0.14)‰[26],粘土礦物分餾值為-0.13‰[22],這使得土壤體系Cd同位素組成的解釋變得復雜。

目前,可用的有機質與水溶液之間的Cd同位素分餾只有Zhao等人[21]的計算和Ratié等人[6]的實驗。Zhao等人[21]計算的Cd同位素分餾為正值,表明有機質更傾向富集重Cd同位素,這與我們的結果相反(圖4),這是因為他們的計算中使用的是隱式溶劑模型,而不是顯示溶劑模型。這可能導致Cd原子周圍局部結構的不精確表達,這對同位素平衡分餾計算是極為重要的。Ratié等[27]認為當Cd與腐殖酸的羧基位點形成配合物時,Cd同位素分餾為(-0.15±0.01)‰,這與我們關于乙酸和苯甲酸體系的計算是一致的。

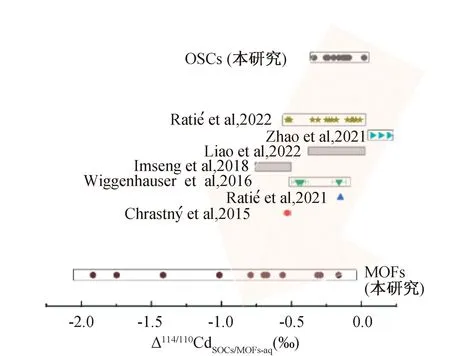
圖4 含Cd有機物-溶液之間同位素平衡分餾

3 結論

25 ℃以下,有機質表面配合物(OSCs)與水溶液之間的Cd同位素平衡分餾較小且不敏感,即Δ114/110CdOSCs-aq=-0.34‰～0.02‰。相比之下,金屬-有機框架(MOFs)的形成產生了顯著的Cd同位素分餾,即Δ114/110CdMOFs-aq=-1.92‰～}。當將OSCs和MOFs視為兩個端元時,OSCs和MOFs信號的二元混合模型可以合理地解釋已發表的有機質土壤的Cd同位素組成測定結果。