火箭儀器艙結構模型的熱振耦合模擬方法

薛景天，董龍雷*，劉 振，趙建平，丁鎮軍，王瀟屹

（1.西安交通大學 復雜服役環境重大裝備結構強度與壽命全國重點實驗室，西安 710049；2.北京強度環境研究所，北京 100076； 3.火箭軍某部，西安 710407）

0 引言

在火箭飛行過程中，其機體結構表面與高速氣流摩擦會產生氣動加熱現象。氣動加熱環境對火箭的影響主要體現在兩方面：一是可能改變火箭結構本身的動力學特性；二是向內傳熱使結構內部的儀器或元器件升溫甚至受損失效，從而影響火箭的可靠性。目前，針對火箭本體結構的氣動加熱防護已有相對成熟有效的措施[1]。而熱環境對航天器結構的動力學特性影響主要體現在對結構固有頻率的影響，Heeg 等[2]對典型的航天飛機真實飛行狀態進行研究并發現，航天飛機表面溫度可以從常溫升至2700 ℃以上，相應地，結構固有頻率及阻尼也可劇烈變化高達30%以上。工程中常利用數值仿真與試驗相結合的方法對結構進行熱振分析[3-10]，但在有關研究中普遍存在的問題是：進行傳熱分析時將結構材料的熱特性參數視為常量，但實際上材料的熱特性參數（如熱導率和比熱容）在傳熱過程中并非恒定不變，而是會隨溫度的變化發生改變；即使考慮到此影響而將這些材料參數設為變量，依然無法保證真實反映材料參數的變化，導致熱振耦合特性預示出現偏差。

本文提出一種材料熱特性參數與振動動態耦合的分析方法，在進行結構傳熱分析中考慮材料熱特性隨溫度的變化，同時結合振動方程，對某火箭儀器艙氣動過程進行熱振耦合機理分析。

1 熱振耦合機理分析

在火箭的飛行過程中，針對熱環境對火箭結構的影響：一方面要關注固有頻率對結構動力學特性的影響；另一方面要關注結構傳熱過程，從而對結構內部元器件和部件的溫度變化做出預示。常規的結構動力學分析是從振動方程出發[7]。然而，本文所討論的是結構的固有特性，與外力無關，并且為簡化模型而忽略結構自身的阻尼項，因此振動方程中的阻尼和激勵項為0，對結構的模態分析可以圍繞公式

展開，其中：K為結構的總剛度矩陣；M為結構的質量矩陣。

加入溫度場變化的主要影響體現在改變振動方程中的剛度項：一方面，溫度的改變使材料的彈性模量發生改變，進而影響結構的剛度，即

式中：B為幾何矩陣；DT為與材料彈性模量ET和泊松比μ有關的彈性矩陣。

另外一方面，當結構的溫度變化時會產生熱應力并影響結構的剛度，即

式中：G為形函數矩陣；Γ為結構熱應力矩陣。

在實際試驗過程中，溫度場和應力場是同時存在的，故通過模態疊加后結構的剛度可以表示為

或

對于某確定結構而言，其泊松比μ是不變的，而彈性模量ET以及結構熱應力Γ均隨著結構溫度T的變化而發生改變，因此掌握結構溫度的變化規律是研究熱振耦合機理的關鍵。

在飛行過程中，飛行器結構表面與氣體摩擦產生的熱量是通過熱傳導的方式傳遞到結構內部的。熱傳導方程是典型的拋物線型二階偏微分方程（見式(6)），

式中：λ為材料的熱導率；ρ為材料的密度；cp為材料的比熱容。式(6)為笛卡兒坐標下的非穩態導熱方程，反映的是三維非穩態熱傳導的傳熱情況。由式(6)可推導出

式中：T為結構某點的溫度；x,y,z為該點的坐標位置；τ為傳熱時間。式(7)揭示了溫度與位置和傳熱時間的關系，可以得到某一時刻結構的熱分布以及在傳熱過程中結構某點的溫度變化。

溫度T與彈性模量ET間存在映射關系，而材料的熱特性參數（如熱導率λ和比熱容cp）會隨溫度的變化而發生改變。根據溫度-彈性模量以及溫度-熱特性參數這2 組對應關系，可以建立材料的彈性模量和熱特性參數之間的對應關系，

綜上，熱振耦合機理的研究是從熱環境對結構的剛度影響出發，關注影響結構剛度參數中隨溫度的變化而發生改變的量，從而對熱環境下結構的振動特性做出預示。因此，考慮熱特性參數變化的仿真計算更加真實、可靠性更高。

2 閃光瞬態法測量材料熱特性

為在熱振耦合分析中引入材料熱特性的變化，需要得到材料熱特性與溫度之間的對應關系。目前，主要利用穩態法和瞬態法測量材料的熱導率[11]。穩態法根據Fourie 方程直接測量熱導率，但該方法適用的溫度和熱導率范圍均較窄，主要是在中等溫度下測量中低熱導率材料。瞬態法則應用范圍較為寬廣，尤其適合于高熱導率材料在高溫下的測試。閃光瞬態法測量原理見圖1[12]。

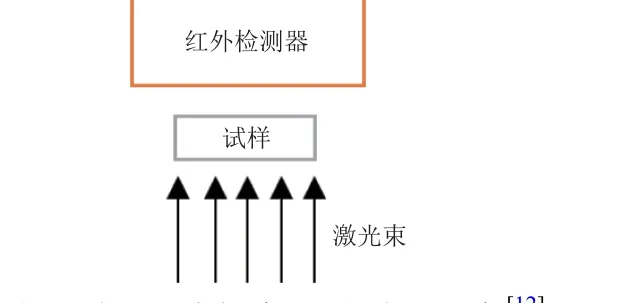
圖1 閃光瞬態法測量原理示意[12]Fig.1 Measurement principle schematic of flash transient method[12]

如圖1 所示，通過儀器向待測試樣底部發出激光束，由試樣上方的紅外檢測器跟蹤監測試樣的升溫過程，得到電信號與升溫時間的關系曲線，通過轉化得到試樣材料熱擴散系數與升溫時間的關系曲線。

式中：α為試樣材料的熱擴散系數；d為試樣厚度；t0為半升溫時間，即試樣溫度達到設定溫度一半所用的時間。

得到材料熱擴散系數后，根據熱擴散系數與熱導率及比熱容的關系，利用已知材料參數的標樣共同進行測試，可推導得到待測試樣材料的熱導率及比熱容。具體方法為：使用一個與待測試樣截面形狀相同、厚度相近、熱物性相近、表面光滑程度相同且比熱容值已知的參比標樣，與待測試樣同時進行表面涂覆；在理想的絕熱條件下，依次進行測量得到2 條測試曲線。由于2 試樣加熱時間相同，因此吸收的熱量可以認為是相同的，故可通過公式(10)得到待測試樣的比熱容。

計算出材料的熱導率λ。

3 數值分析

熱振耦合機理的研究通常包括以下步驟：1）設計模型并進行數值分析；2）設計試驗裝置及夾具，并制定試驗條件；3）完成熱振試驗；4）對試驗結果進行數據處理，包括材料的熱振耦合特性預示。本文詳述開展模型設計并進行數值分析的過程，其余步驟會在之后的文章中進行論述。

3.1 試驗模型設計

以某型號火箭儀器艙為研究對象，建立其幾何模型，如圖2 所示。

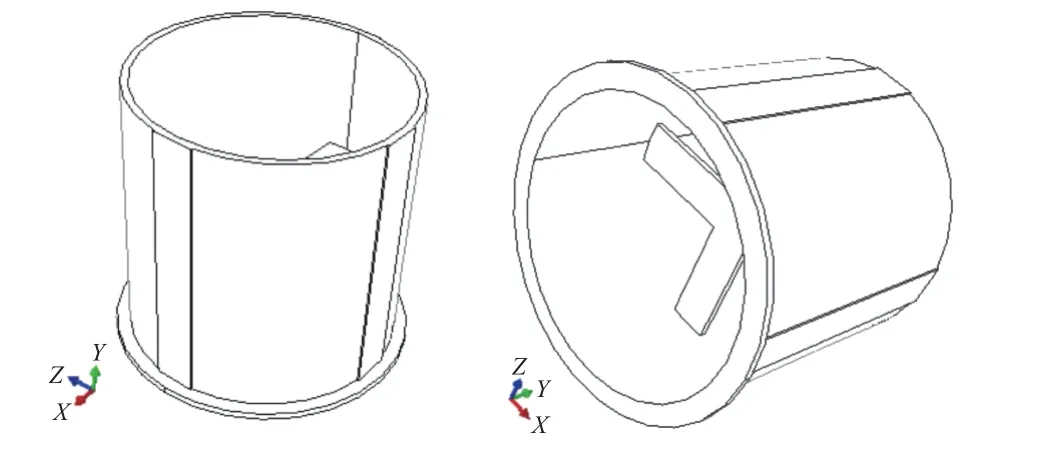
圖2 火箭儀器艙筒形艙段三維模型Fig.2 Three-dimensional model of the rocket cylindrical instrument cabin

筒形艙段由筒與十字梁2 部分結構組成，其中十字梁用來安裝火箭內部部件及其他元器件。對該模型進行數值仿真計算，筒的材料為鋼，通過閃光瞬態法測得的結構材料參數如表1 所示。

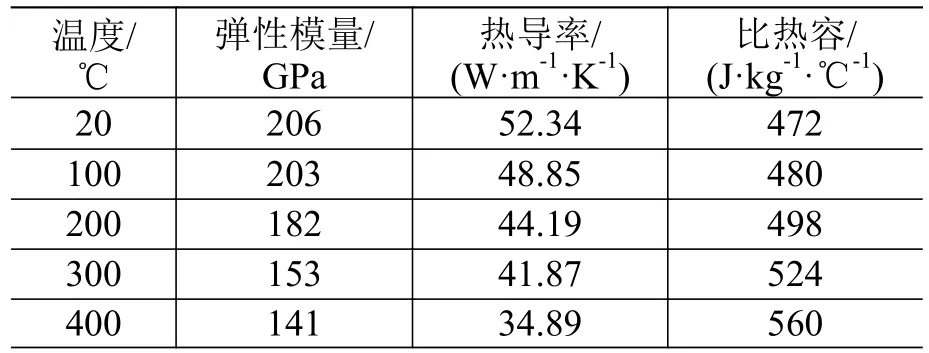
表1 火箭儀器艙筒形艙段的材料參數Table 1 Material parameters of the rocket cylindrical instrument cabin

3.2 數值計算

3.2.1 傳熱計算

本文對筒形艙段模型的處理作出以下假設：

1）筒外側受到均勻溫度場的影響，即結構縱向不存在溫度梯度，可簡化為二維平面；

2）筒的厚度遠小于艙段的長度，即可忽略筒的厚度，將艙段簡化為薄壁殼結構；

3）艙段結構為對稱結構，在傳熱過程中十字梁結構的溫度分布具有對稱性，可簡化為矩形平板。

經上述簡化的筒形艙段傳熱模型如圖3 所示，傳熱過程被簡化為第一類邊界條件的一維熱傳導問題：給定模型外側固定溫度值，分析中間矩形結構部分的溫度與傳熱時間的關系，得到

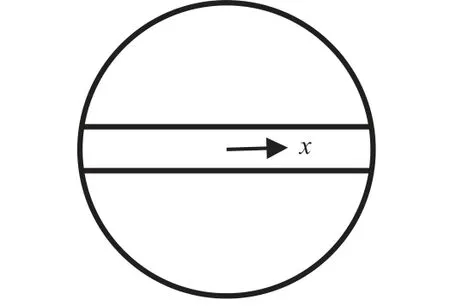
圖3 筒形艙段簡化傳熱模型Fig.3 Simplified heat transfer model of the cylindrical cabin

式中：T為結構某點的溫度；x為該點的坐標位置；τ為傳熱時間。

在實際傳熱過程中，筒外側邊界條件為恒溫400 ℃，結構其他部分的初始溫度為20 ℃，即傳熱的邊界條件為

式中u(x,τ)為與位置和時間相關的傳熱方程，l為筒縱向長度。

采用分離變量法求解該傳熱模型的偏微分方程得到

通過式(14)可以得到模型上各點的溫度變化，即結構上任意位置、任意時刻的溫度值。

在熱振耦合試驗中，通常使用石英燈陣對試件進行溫度加載來模擬飛行器在飛行過程中所受到的氣動加熱。因此需要對所使用的石英燈的個數、功率以及加熱時間等進行傳熱仿真分析。同時，需要通過仿真模態分析對試驗結果的可靠性進行驗證。本研究中，將由閃光瞬態法得到的材料熱特性參數代入有限元計算軟件ABAQUS 進行仿真計算得到結構的溫度分布。熱量以熱傳導方式從筒外側傳遞到結構內部，在十字梁上選取3 個位置的特征點與理論模型計算的結果進行對比，特征點（T1～T3）的位置及結構網格如圖4 所示。在考慮及不考慮材料熱特性（即材料的熱導率和比熱容）隨溫度變化而改變的情況下，計算得到50 000 s 傳熱時間內3 個位置點的溫度變化曲線，如圖5～圖7 所示。

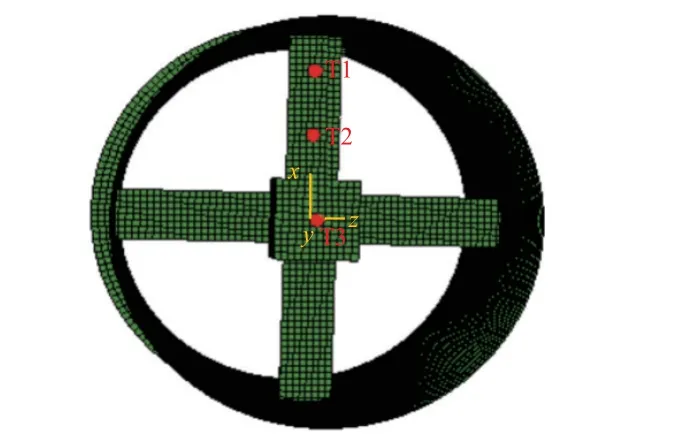
圖4 模型中的特征測點位置Fig.4 Positions of characteristic measuring points on the model

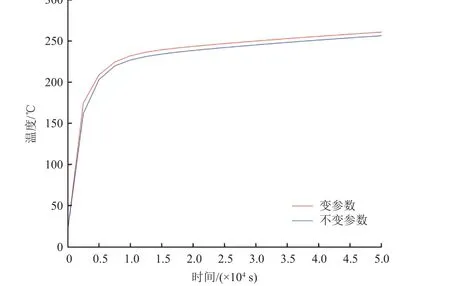
圖5 T1 位置的溫度曲線Fig.5 Temperature curve for T1

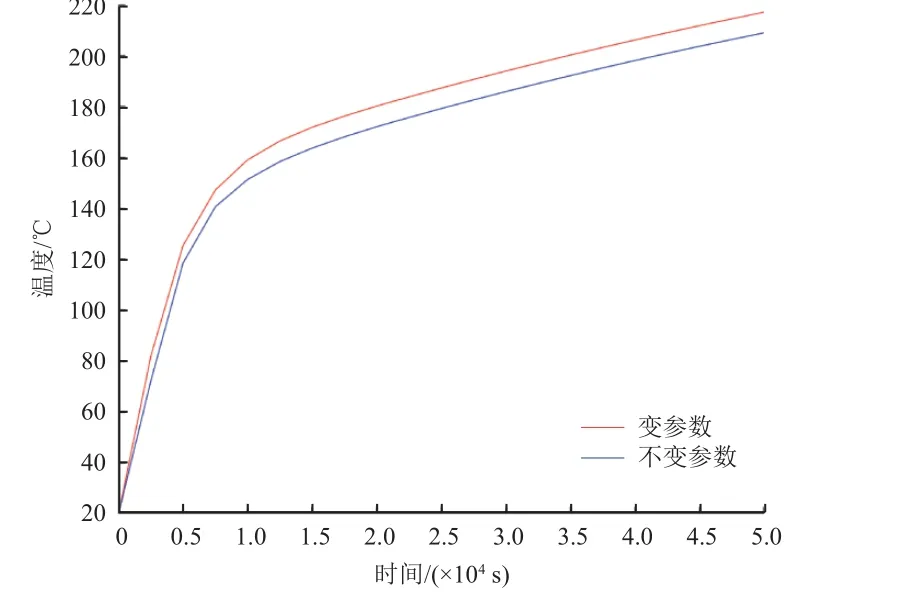
圖6 T2 位置的溫度曲線Fig.6 Temperature curve for T2

圖7 T3 位置的溫度曲線Fig.7 Temperature curve for T3

可以看出，是否考慮材料參數隨溫度的變化對傳熱過程的仿真計算結果有很大的影響，并且越靠近結構中心（即實際安裝儀器位置）的誤差越大。

3.2.2 熱振耦合仿真計算

熱環境對結構模態的影響主要體現在對結構剛度的影響，因此結構剛度在熱環境中的變化規律能夠反映出結構的熱振耦合作用機理。用有限元方法對結構進行模態分析時會對結構的剛度矩陣和質量矩陣進行計算，對比不同溫度場下輸出的結構剛度矩陣可得到結構在熱環境中的剛度變化。由于輸出矩陣的單元數過多，選出前50 個單元的剛度矩陣大小繪制曲線，如圖8 所示。

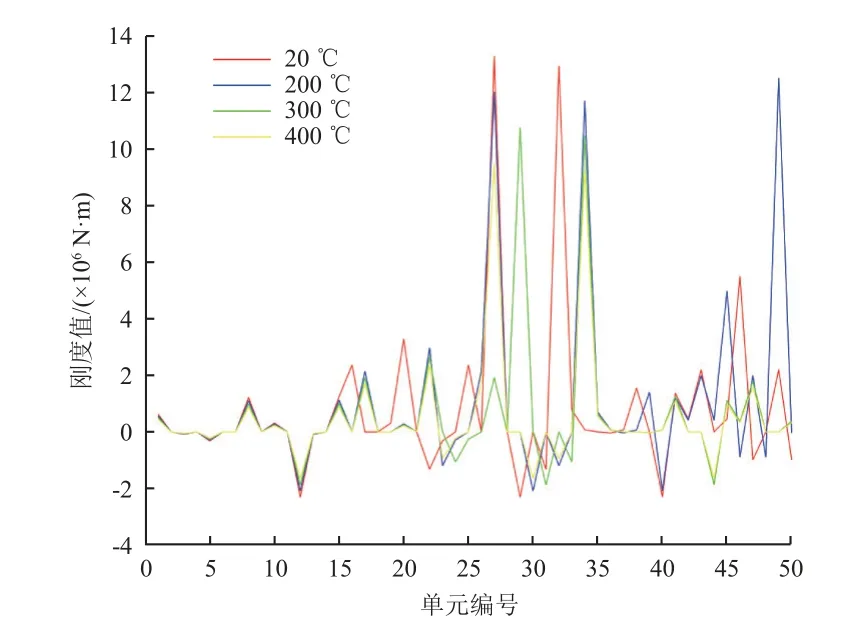
圖8 不同溫度下的結構單元剛度曲線Fig.8 Stiffness curves of structural units at different temperatures

從圖8 可以看到，典型結構的前50 個單元的剛度隨溫度變化發生明顯改變：一方面，剛度曲線的峰值發生了改變，總體表現在隨著溫度的升高，剛度的峰值降低，符合仿真分析計算結果；另一方面，剛度曲線峰值的位置發生了改變，甚至有峰值缺失或者增大現象。由此可見，溫度對結構剛度的影響不僅僅體現在數值大小的變化上，還會改變結構剛度的最值位置。因此，在實際結構設計中，通過剛度計算可以預示在不同溫度場下的結構剛度薄弱位置，為更深層次的熱振耦合機理研究奠定基礎。

將計算的溫度場結果作為預定義場導入熱應力計算中，在溫度場和熱應力場疊加作用下進行模態計算，得到結構的振型和固有頻率。在進行網格無關性檢驗后得到的網格數計算結果收斂性良好。設定4 種溫度工況（20 ℃、200 ℃、300 ℃和400 ℃），得到溫度場、應力場以及2 個場共同作用對結構固有頻率的影響，結果表明模態振型沒有明顯變化，不同溫度下結構的前6 階固有頻率如表2 所示。

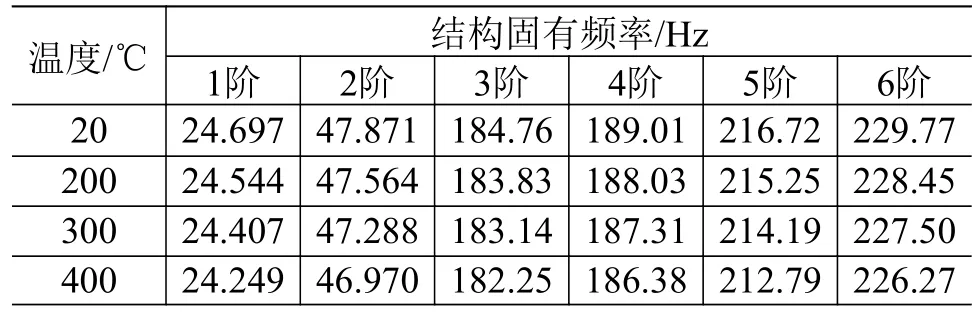
表2 不同溫度下結構的前6 階固有頻率Table 2 The first six natural frequencies of the structure at different temperatures

4 結束語

本文提出一種材料熱特性參數與振動動態耦合的分析方法，用來提高傳熱分析的精度以及獲取熱環境下結構的振動特性。針對某火箭筒形儀器艙段結構進行建模以及仿真計算，首先進行傳熱計算，得到溫度分布后計算結構的熱應力，然后在溫度場和應力場疊加情況下進行結構模態分析，并對比不同熱環境下的計算結果。結果顯示：

1）針對該結構，在計算過程中考慮材料的熱特性參數隨溫度的變化可提高結構傳熱仿真精度，繼而提高結構熱振耦合分析的溫度場加載準確性。

2）熱環境對火箭儀器艙結構的影響主要體現在結構固有頻率隨溫度升高小幅降低，對結構的振型基本沒有影響。溫度場升高使材料熱退化導致結構的固有頻率下降，由于溫度場產生的熱應力導致結構的固有頻率上升，而對火箭儀器艙的熱振耦合分析顯示溫度導致的材料熱退化占主導地位。

綜上，考慮材料熱特性隨溫度變化的動態熱振耦合方程可提高傳熱仿真分析的精度和可靠度，可為建立熱振耦合試驗裝置提供參考，并可推廣到火箭儀器艙在熱環境中的動力學特性變化的預測中。