深海無人系統大長徑比環肋圓柱殼結構設計與試驗研究

陳沙古，高 原，吳智睿，郁 偉，周 成，劉 成

（1.中國船舶科學研究中心，江蘇 無錫 214082；2.深海技術科學太湖實驗室，江蘇 無錫 214082）

耐壓結構是水下裝備系統的關重件，用來集成搭載設備單元、電子元器件及傳感器等，為其提供常壓環境，保證其不受海水壓力和腐蝕的影響，因此耐壓結構需要具備足夠的強度和可靠的密封［1-4］。環肋圓柱殼是一種最為典型的耐壓結構，也是深海無人系統廣泛采用的耐壓結構形式。

受靜水壓力的閉合環肋圓柱殼應力一般是采用基于薄殼理論的軸對稱圓柱殼彎曲微分方程［5-7］來研究。典型的簡化力學模型有兩種：一種是不考慮肋骨布置和形狀差異，將環肋視為圓柱殼梁的彈性支座，假定環肋的形心與圓柱殼殼板形心重合，環肋的作用以肋骨橫剖面面積的方式折算到殼板中曲面上；另一種是將環肋圓柱殼分解為肋骨腹板（二維環板）、肋骨翼板（一維圓環）和圓柱殼3 部分進行聯立求解［8］。目前中國現行的潛艇、潛水器等耐壓結構設計標準基本是基于上述兩類簡化力學模型建立的［9-10］。關于環肋圓柱殼耐壓結構的應用設計研究，針對潛艇或潛水器結構，其長徑比（L/D）通常較小，往往不大于3［11-12］。隨著深海耐壓結構的應用需求，環肋圓柱殼艙段長度有不斷增加的趨勢，長艙段環肋圓柱殼艙段的穩定性問題將更為突出。長艙段環肋圓柱殼主要應用于較大深度的水下環境，其結構力學特性的計算方法可以參考普通環肋圓柱殼；然而長艙段與普通環肋圓柱殼結構參數的不同，所受外部壓力亦較普通環肋圓柱殼有較大的增加，造成普通環肋圓柱殼結構力學特性計算方法不完全適用于長艙段耐壓結構設計［13］。

這里以一種超長型深海無人系統耐壓結構設計為例，圍繞大長徑比環肋圓柱殼的結構形式、設計計算、仿真分析、模型驗證等開展研究，為該型深海無人系統結構設計提供技術支撐，也為其他類似耐壓結構設計提供參考。

1 結構設計要求

為滿足該型深海無人系統內部單元、元器件等設備的安裝空間和接口要求，環肋圓柱殼耐壓結構的主要設計指標如下［14］：

1）圓柱殼內直徑1.0 m，耐壓結構長度不小于11.0 m，長徑比L/D大于11；

2）最大外徑不超過1.4 m。

2 結構形式

這里的圓柱殼艙段長度L與其直徑D之比（L/D）很大，是超長型圓柱殼結構，為提高圓柱殼結構的強度與穩定性，利用間隔布置環形肋骨的方式對其進行加強。肋骨加強有2 種，如圖1 所示：一是采用特大肋骨與普通肋骨組合的加強方式；二是大肋骨的加強方式。為適應深海無人系統整體外形的約束要求（最大外徑不超過1.4 m），并兼顧耐壓結構外部浮力材料、電纜的敷設需要，圓柱殼結構布局上不宜采用特大肋骨形式。因此，這里圓柱殼結構確定采取大肋骨加強形式。

圖1 圓柱殼結構肋骨加強形式示意Fig.1 The rib type of cylindrical shell structures

3 結構設計

該深海無人系統耐壓結構的材質為某高強度鋼材料，材料彈性模量取1.96×105MPa，泊松比為0.3。

根據相關方法［7-10］，圓柱殼結構的殼板厚度t應滿足關系式：

式中：pc為計算壓力；σs為材料屈服強度；R為圓柱殼內半徑；K2，0為應力系數。

當R=500 mm、pc取15 MPa時，按系數K2，0=1.1進行殼板厚度估算，代入參數可得：

當圓柱殼半徑R=500 mm，彈性模量E=1.96×105MPa，泊松比μ=0.3，殼板厚度t=14 mm 時，肋骨間距l滿足關系式：

根據現行相關標準［9］方法分析肋骨慣性矩的取值要求，為保證環肋圓柱殼艙段不發生總體失穩，有

因此可以得出計及殼板帶寬的肋骨慣性矩I應滿足：

顯然，肋骨間距l越大，肋骨慣性矩要求越大。

這里圓柱殼結構肋骨之間的耐壓殼板上需要開設一定數量的開孔圍壁，用于保障耐壓結構內外的電纜穿艙。結合式（6），并兼顧考慮開孔圍壁的設計與工藝需求，肋骨間距取為l=400 mm。當肋骨型材取時（分子為T型肋骨面板的寬度×厚度；分母為T型肋骨腹板的高度×厚度），可以滿足式（10）慣性矩的要求。因此，可以得到環肋圓柱殼結構方案如圖2所示，設計參數匯總如表1所示。

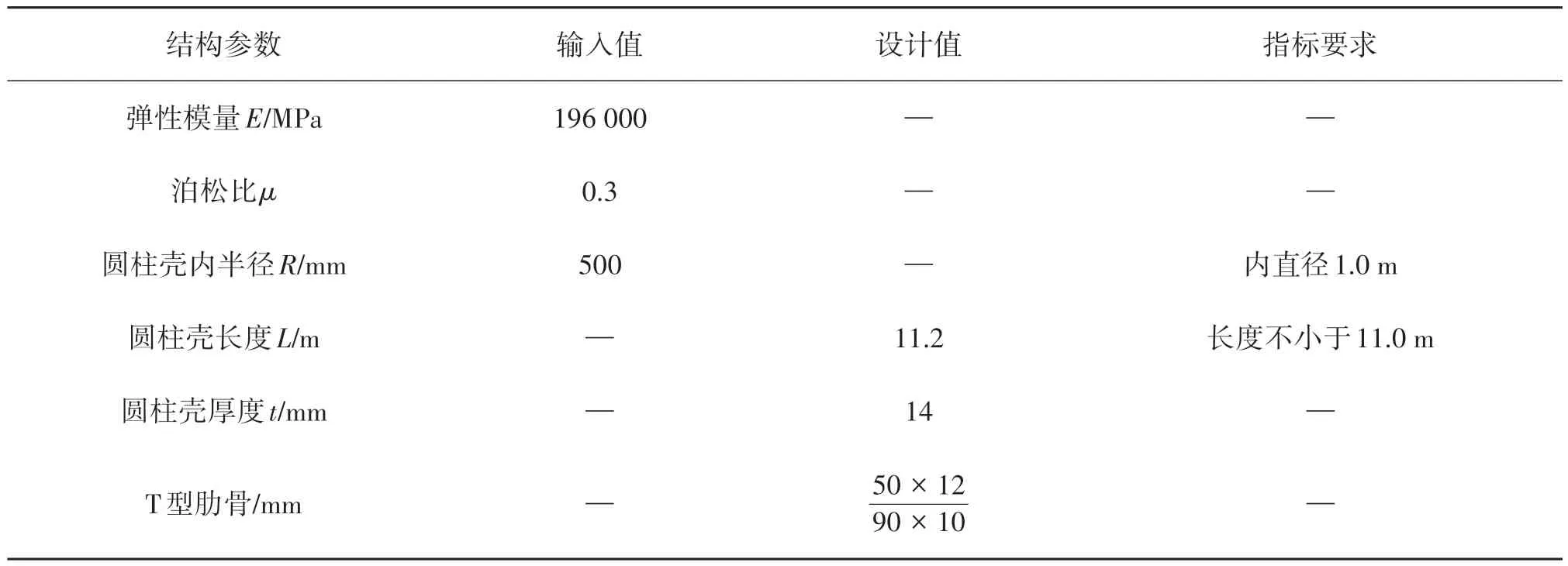
表1 環肋圓柱殼結構設計參數匯總Tab.1 Structural design parameters of the ring-stiffened cylindrical shell

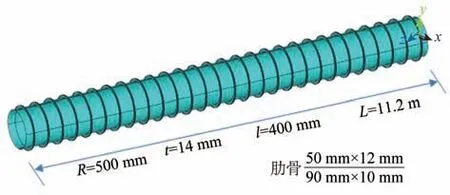
圖2 環肋圓柱殼結構設計方案Fig.2 The design scheme of the ring-stiffened cylindrical shell

4 結構強度與穩定性計算

參考現行相關標準方法［9-10］，對環肋圓柱殼結構的典型應力強度和穩定性進行計算，該大長徑比環肋圓柱殼結構的計算結果見表2（表中的負值表示為壓應力，材料屈服強度σs取為785 MPa），結果表明其應力強度和穩定性滿足相關強度標準要求。

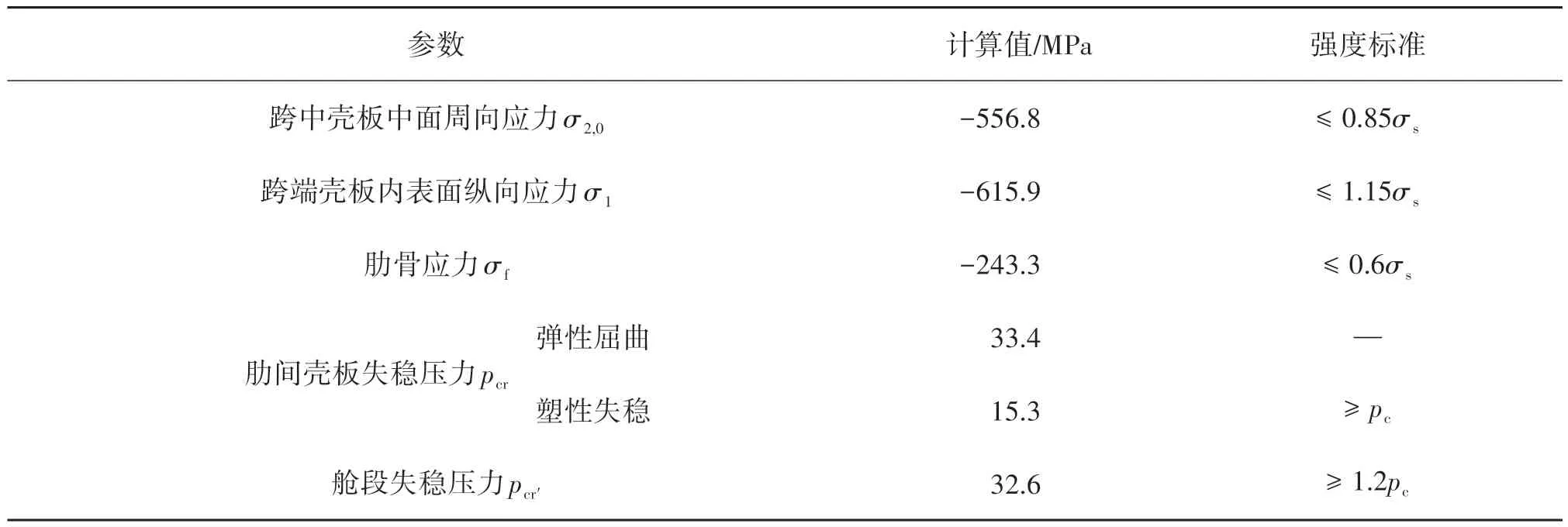
表2 環肋圓柱殼結構強度與穩定性計算結果Tab.2 Calculation results of strength and stability of ring-stiffened cylindrical shell

進一步采用有限元軟件對其進行數值仿真計算，選用shell163殼單元建模，有限元模型如圖3所示，單元劃分網格10 mm×10 mm，在模型圓柱殼表面施加面載荷pc，模型一端的端部節點施加固支位移約束，模型另一端的端部節點施加UX、UY位移約束（x，y方向的位移為0），并施加軸向壓作用力Fz，Fz=-pcπR2/N，N為端部節點數量。

圖3 環肋圓柱殼結構有限元模型Fig.3 The finite element model of the ring-stiffened cylindrical shell

在計算壓力pc載荷下，環肋圓柱殼結構的仿真云圖如圖4所示，計算結果表明：

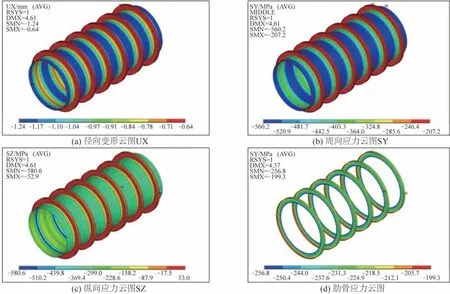
圖4 環肋圓柱殼結構仿真計算云圖Fig.4 The simulation results of ring-stiffened cylindrical shells

1）圓柱殼結構的徑向收縮最大變形為1.24 mm，發生在相鄰肋骨的跨中位置；而在軸向方向上，其結構整體變形收縮量約為7.30 mm。

2）相鄰肋骨間跨中耐壓殼板中面周向應力為-560.2 MPa。

3）肋骨根部耐壓殼板內表面縱向應力為-580.6 MPa。

4）肋骨面板應力為-234.0 MPa，肋骨腹板根部應力為-256.8 MPa，肋骨平均應力為-245.4 MPa。

對環肋圓柱殼結構進行彈性屈曲計算，屈曲模態云圖如圖5所示。計算結果表明，環肋圓柱殼結構的彈性屈曲壓力為35.9 MPa，失穩模式為圓柱殼肋間局部失穩。

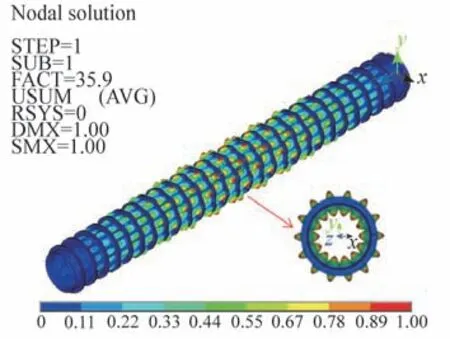
圖5 環肋圓柱殼結構彈性屈曲模態Fig.5 Elastic buckling modes of ring-stiffened cylindrical shell

對環肋圓柱殼結構進行極限承載能力計算，在前述彈性屈曲計算的屈曲模態上導入幾何初始缺陷，設置初始缺陷的幅值為0.15t（即2.1 mm），同時設置材料的屈服強度為785.0 MPa，利用弧長法進行非線性屈曲分析。環肋圓柱殼結構極限承載能力計算結果如圖6所示，失穩壓力為15.1 MPa。

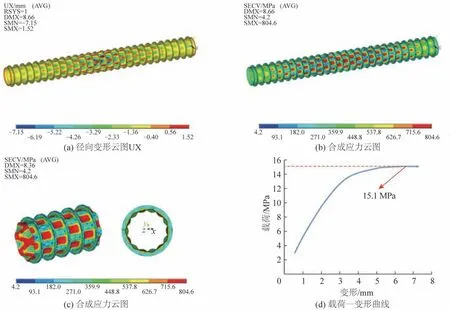
圖6 環肋圓柱殼結構彈塑性計算結果Fig.6 Elastic-plastic calculation results of the ring-stiffened cylindrical shell

表3 給出了采用理論方法和數值仿真方法環肋圓柱殼結構強度與穩定性計算結果，兩種方法的計算結果基本一致，證明了設計計算的正確性。

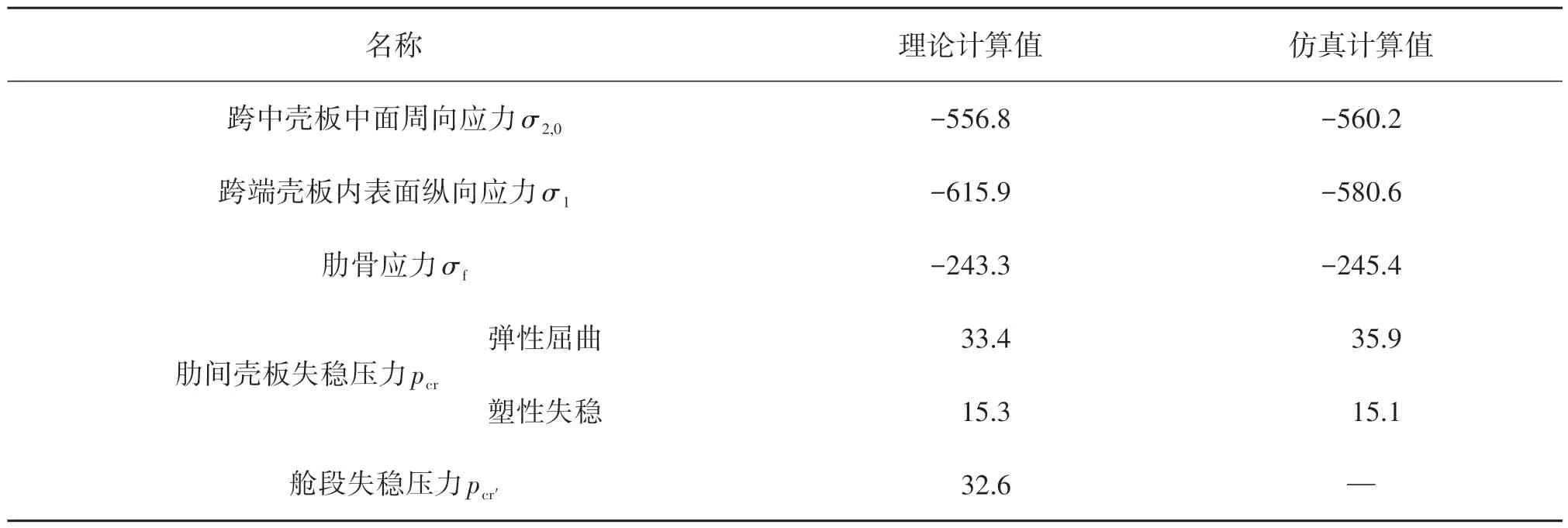
表3 環肋圓柱殼結構強度與穩定性計算結果匯總Tab.3 Calculation results of strength and stability of the ring-stiffened cylindrical shell 單位： MPa

5 結構模型試驗

為驗證環肋圓柱殼結構設計，研制結構模型開展水壓試驗研究，模型實物如圖7所示。通過電阻應變傳感器，在模型試驗過程中對其典型部位進行了結構應力應變響應監測，圖8為模型試驗時應變測點的壓力—應變曲線，結果表明其呈現良好的線性和回復性，可以根據應變測量值由胡克定律估算結構應力。

圖7 環肋圓柱殼結構模型照片Fig.7 The photo of the ring-stiffened cylindrical shell

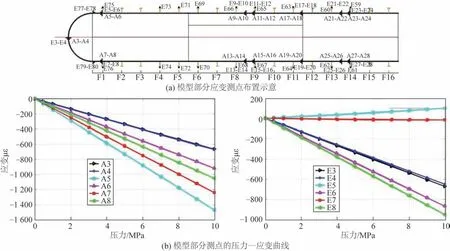
圖8 模型試驗時應變測點布置及各測點壓力—應變曲線Fig.8 The layout of strain measuring points and the pressure-strain curves of each point during model tests

根據試驗結果，可以推算出計算壓力下的模型結構應力，試驗結果表明：

1）肋骨面板應力最大值為-231.4 MPa，測點平均值為-221.6 MPa，詳見表4所示；

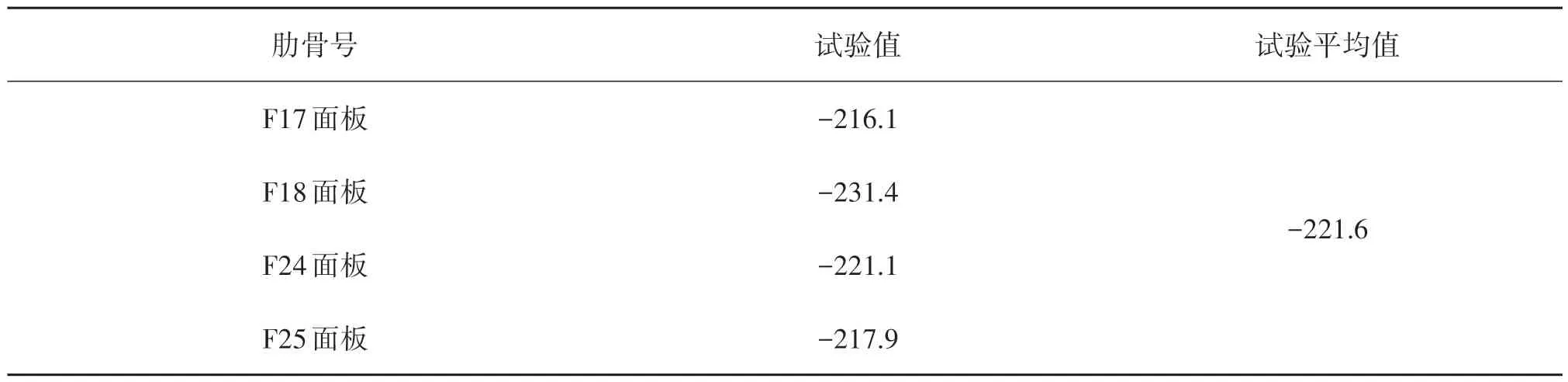
表4 肋骨面板應力試驗值Tab.4 Test results of rib stress 單位： MPa

2）跨中殼板中面周向應力最大值為-589.1 MPa，平均約為-565.2 MPa，詳見表5所示；

3）跨端殼板內表面縱向應力最大值為-580.8 MPa，平均約為-559.3 MPa，詳見表6所示。

將模型試驗結果與計算值進行比較，具體見表7，結果表明：

表7 模型應力試驗值與計算值比較Tab.7 The comparison of model stress test values with calculated values 單位： MPa

1）跨中殼板中面周向應力試驗平均值為-565.2 MPa，與模型的理論計算值、仿真計算值較為一致；

2）跨端殼板內表面縱向應力試驗平均值為-559.3 MPa，其試驗結果要略小于模型理論計算值，這是因為在跨端肋骨根部存在角焊縫，應變測點布置雖然抵近肋骨根部焊縫，但該處應力梯度較大，其試驗測得的結果不是最大值；

3）肋骨面板應力平均值為-221.6 MPa，該處給出的模型理論計算值為肋骨根部對應的肋骨應力，由于是外肋骨，肋骨根部的肋骨應力最大、肋骨面板的肋骨應力最小，提取肋骨面板應力仿真計算值（-234.0 MPa）與模型試驗結果較為一致。

6 結 語

針對大長徑比環肋圓柱殼結構開展了結構設計、計算分析及試驗驗證等研究，主要結論如下：

1）綜合兼顧超長型深海無人系統的外形約束和外部布置需求，該大長徑比環肋圓柱殼宜采用大肋骨的加強結構形式。

2）參考現行相關標準方法，提出了滿足設計指標的環肋圓柱殼結構設計方案，通過數值仿真和模型試驗，綜合驗證了結構計算分析的正確性和有效性。

3）大長徑比環肋圓柱殼結構設計的有關計算分析結果，可以為超長型深海無人系統結構設計提供技術支撐。