考慮翹曲應力的半潛平臺扭轉極限強度計算方法研究

吳劍國，黃燁斐，劉成名，張 萌，朱熠凡

（1.浙江工業大學 土木工程學院，浙江 杭州 310023；2.中國船級社海工技術中心，天津 300457）

半潛平臺是石油勘探開發的關鍵海上裝置，它由甲板平臺、浮體、立柱和撐管組成，其中間甲板部分還存在著大開口，各個剖面的結構差異較大，扭轉剛度較低，因此半潛平臺的扭轉極限強度研究十分重要。

目前半潛平臺扭轉極限強度計算主要采用建立平臺整體模型的有限元方法。張延昌等［1］就半潛平臺極限強度有限元分析方法、初始變形影響、結果分析等技術進行了研究，計算了平臺在橫向分離、縱剪、縱扭三種變形模式下的極限承載力。Ye等［2］采用三維有限元整體模型，使用ANSYS非線性有限元分析了半潛平臺不同工況下的極限承載力。劉帆等［3］研究了不同組合比例的剪切扭轉組合載荷對平臺整體極限承載力的影響，并用隱函數擬合得到了單一載荷和組合載荷下整體極限承載力的聯合關系式。余洋喆［4］使用非線性有限元方法，確定了整體平臺結構在橫向受力模式、縱向剪切模式、扭轉模式及剪切扭轉耦合模式的極限承載力、失效模式及主要承載力構件，并通過不同初始載荷比例的計算，確定了剪切和扭轉組合的耦合方程。趙南等［5-6］進行了壓扭聯合載荷作用下撐桿結構極限強度模型試驗與有限元分析，獲得撐桿結構在壓扭聯合載荷作用下的極限承載能力。由于半潛平臺結構復雜，其整體模型的建立和計算都十分耗費時間，且收斂性較差，如何縮小模型范圍，提高約束扭轉極限強度的計算效率是業界普遍關心的問題。

翹曲應力是影響約束扭轉強度［7-11］的一個重要因素，而模型長度又影響翹曲應力的大小。現階段對于半潛平臺方面的翹曲應力研究尚未見報道；在船體梁方面，約束扭轉極限強度計算的有限元模型長度一直存有爭議。Paik 等［12］對比一跨與一艙模型的有限元結果，發現一艙模型值略小于一跨計算結果，認為一跨模型計算結果大致可以代表一艙的極限承載力。姬振華［13］采用有限元方法分析了大開口船體梁的約束扭轉極限強度以及失效模式，認為計算船體梁約束扭轉極限強度的模型要比船體梁彎曲失效的模型在船長方向大得多，至少要包括整個開口區域，而不能只是兩個強框架范圍的船體梁。Ao和Wang［14］對3根不同跨長的箱型梁截面進行了有限元分析，討論了模型初始缺陷、網格細化、加強筋和初始撓度對扭轉的影響，并提出了簡化計算方法。Sun和Soares［15］通過兩條大開口的船體梁縮尺模型試驗，研究船體梁在扭轉過程的失效模式，發現扭轉過程中最先發生破壞的是甲板的角隅部位。Wang 等［16-17］通過對一艘10 000TEU 集裝箱船的模型扭轉試驗，發現集裝箱船在扭轉過程中主要以兩側壁剪切失效為主，船底板部分尚未到達極限狀態，整體截面已經失效，且發現船體梁在扭轉過程中會發生翹曲變形和剪切屈服。Wang 和Wang［18］研究了船體梁扭轉逐步破壞過程中翹曲的影響，根據不同跨數有限元模型的結果，擬合得到了船體梁約束扭轉極限強度隨跨數變化的計算公式。

在薄壁梁約束扭轉極限強度理論分析方面，吳劍國等［19］將薄壁梁視為一系列由主要支撐構件和扶強材支撐的板格，假設極限狀態時所有板格都達到了板格的極限狀態，利用板格的極限承載力計算公式計算極限剪應力，并結合薄壁梁極限狀態時的剪流方向假設，提出了薄壁梁截面約束扭轉上限的簡化計算公式。吳劍國等［20］、李鈞暉［21］建立了約束扭轉過程中加筋板剪應力與剪應變的關系，提出了船體梁約束扭轉極限強度計算的簡化逐步迭代方法，但該方法未考慮翹曲應力對約束扭轉極限強度的影響，僅適用于翹曲應力較小的船舯部位。故目前工程上需要一種考慮翹曲應力的半潛平臺極限狀態簡化計算方法。

為了提高半潛平臺約束扭轉極限強度的計算效率及收斂性，這里進行半潛平臺整體有限元模型的簡化研究，討論了模型長度和單元大小對平臺約束扭轉極限強度的影響。基于薄壁桿件力學理論［22-23］，開展扭轉極限狀態下半潛平臺翹曲應力的簡化計算，進行考慮翹曲應力影響的半潛平臺約束扭轉極限強度的計算方法研究。研究成果對提高半潛平臺結構安全性、降低其營運風險有一定的科學意義和工程應用價值。

1 半潛平臺約束扭轉極限強度計算的有限元方法

由于半潛平臺在縱扭工況下，主要由平臺甲板和橫撐兩部分提供抗扭剛度，其中又以平臺甲板為主，故這里主要研究平臺甲板模型長度及單元大小對其約束扭轉極限強度計算結果的影響，以及橫撐提供的縱扭承載力計算方法。

1.1 平臺與甲板的有限元模型

該半潛平臺的主尺度如表1所示。整體模型采用AH32高強度鋼，彈性模量為206 GPa，泊松比為0.3，材料假設為理想彈塑性模型。詳細的結構尺寸見文獻［4］。

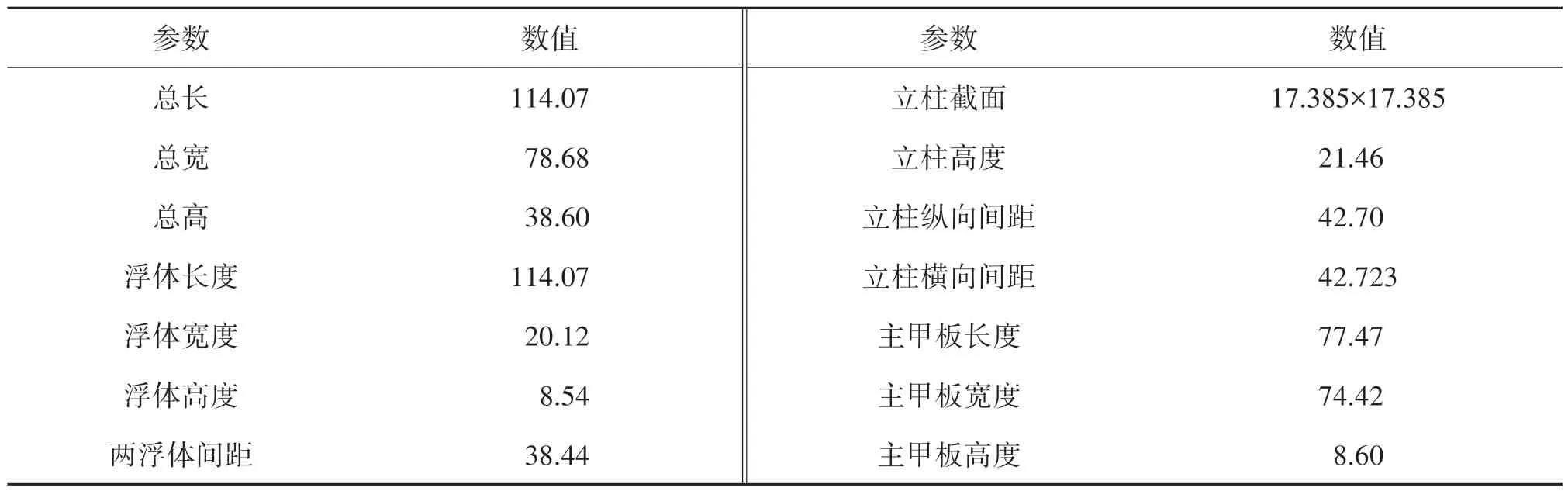
表1 半潛平臺主尺度Tab.1 The main dimensions of containership 單位： m

分別進行了整體模型、4種長度的甲板模型、細化的單跨甲板模型、細化的立柱間甲板模型，共計7種模型的非線性有限元計算。模型中板單元都采用S4R單元，S4R單元為四邊形四結點曲殼單元，可用于薄殼或厚殼結構建模，采用減縮積分方式，包含沙漏模式控制，容許有限薄膜應變。各模型的寬度均相同，扭轉的邊界條件設置見表2，主要區別如下：

表2 邊界條件與加載方式Tab.2 Boundary conditions and loading methods

1）整體模型及邊界條件。鑒于平臺抗扭的薄弱部分是立柱間的甲板，因此總體模型僅包含中間甲板以及橫撐部分，如圖1（a）的綠色部分；而將剛度很大的浮體和立柱以及相連的甲板全部剛化，如圖1（a）的藍色部分。左右兩側剛化部分分別耦合至平臺甲板最外側截面的形心處，并在兩端的耦合點上分別施加約束與轉角。整體模型的單元邊長約為1.5 m，僅包含甲板板、艙壁板等板材以及較大桁材的腹板，不包括較小桁材、骨材、面板等結構，詳見圖1（b）。

圖1 模型及邊界條件示意Fig.1 Schematic diagrams of model and boundary conditions

2）為了分析撐管、甲板長度對計算結果的影響，建立了甲板模型1～4。甲板模型1 除了沒有撐管外，其他與整體模型相同；甲板模型1～4的長度逐步減小，詳見圖1中的（c）～（f）。

3）一跨細化甲板模型是取甲板模型1 中靠近邊跨區域的一跨模型細化而成，并增加了縱向骨材。長度與甲板模型4的長度相同。細化模型的單元邊長約為0.15 m，包含縱向骨材，骨材之間的長度設置4個單元，骨材腹板高度最少劃分3個單元，加筋肋根據翼緣剖面形狀劃分為2～3個單元，詳見圖1（g）。

4）立柱間甲板細化模型是將一跨細化甲板模型加長至甲板模型1 的長度，并增加了橫向構件。立柱間甲板細化模型詳見圖1（h）。

1.2 有限元結果分析

采用兩倍彈性斜率準則［1］確定半潛平臺縱扭工況的極限承載力。7 種模型有限元結果見表3。極限狀態應力云圖與載荷—變形曲線見圖2～3，為了體現計算模型的大小和位置，圖2（a）和圖3（a）～（d）保留了計算模型之外的剛化區域，如圖中藍色區域所示，這部分是不參與計算的。

圖2 扭轉極限狀態模型應力云圖及轉角曲線Fig.2 Stress diagrams and angle curve diagrams of torsion limit state model

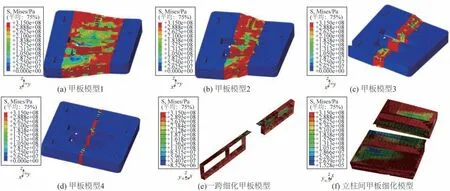
圖3 各種甲板模型扭轉極限狀態應力云圖（變形放大4倍）Fig.3 Stress contour maps at the ultimate limit state for various deck models(deformation magnified by 4 times)

結果表明：

1）對比整體模型與甲板模型1的結果可以發現，橫撐對約束扭轉極限承載力影響不大，大約11%左右。

2）對比甲板模型1、2、3、4的結果可知，模型長度越小模型極限承載力越大，說明必須考慮翹曲應力對約束扭轉極限強度的影響。

3）對比一跨細化甲板模型與甲板模型4、立柱間甲板細化模型與甲板模型1 的結果可知，單元大小對約束扭轉極限強度計算的結果影響小于20%。

1.3 縱扭極限狀態時橫撐的作用

由于上部甲板的剛度比下部橫撐的剛度大得多，故當上部甲板到扭轉極限時橫撐還未到達極限狀態。半潛平臺在縱扭工況時，橫撐可簡化為兩端相對錯動但不能轉動的梁，力學模型如圖4所示。

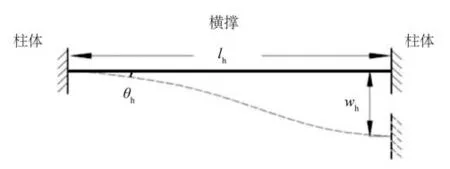
圖4 橫撐受力示意Fig.4 Force diagram of the lateral support on shear conditions

錯動量可近似采用式（1）計算：

式中：wh為橫撐橫向位移，mm；θh為極限狀態下橫撐轉角，近似取前文縱扭工況下甲板模型1的有限元結果；lh為橫撐長度，mm。

根據橫撐的力學模型，其剪切承載力FQh計算公式如下：

式中：Ih為橫撐慣性矩，mm4；E為材料彈性模量，MPa。

由此得橫撐所能提供的扭轉承載力Tuh近似計算為式（3），計算結果見表4，誤差為3%，精度較高。

表4 橫撐在縱扭工況極限承載力匯總Tab.4 The ultimate capacity summary of lateral support on torsion conditions

2 半潛平臺翹曲應力理論計算方法

從薄壁桿件力學理論入手，提出了半潛平臺扭轉極限狀態下翹曲應力的簡化計算方法。

2.1 翹曲應力的簡化計算方法

由于半潛平臺截面是一個具有大開口、多閉室的截面，如圖5（a）所示，為簡化計算，這里將半潛平臺截面整體簡化為一個大開口的矩形截面，矩形截面取半潛平臺最外圈甲板及舷側進行計算，上下開口處板厚記為0，其余板厚與實際厚度相同，如圖5（b）所示。計算過程如下：

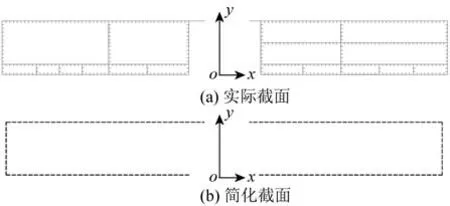
圖5 半潛平臺實際及簡化截面Fig.5 Actual and simplified sections of the semi-submersible platforms

1）求矩形截面各個位置的翹曲應力σω

按薄壁結構彈性理論［23-24］求得的矩形截面各個位置的翹曲應力為：

式中：B為截面位置處的雙力矩；ω為廣義主扇性面積；Iω為截面廣義主扇性慣性矩。

2）求矩形截面極限狀態的翹曲應力

如果按上式計算的板格翹曲應力大于其屈服強度，說明此處板格已進入塑性，則根據理想彈塑性模型認為翹曲應力不再增加。

2.2 半潛平臺翹曲應力計算結果對比

一跨與立柱間甲板有限元模型的翹曲應力云圖如圖6所示，由圖可知：

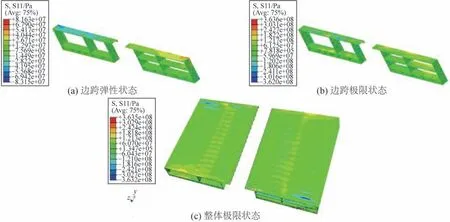
圖6 翹曲應力云圖Fig.6 Warpage stress nephogram

1）半潛平臺翹曲應力沿全長分布為加載兩端較大、中間截面較小，破壞發生在加載兩端的邊跨，總體呈現反對稱分布。

2）彈性狀態與極限狀態下的翹曲應力分布規律是一致的，僅極限狀態下翹曲應力值變大，部分板格翹曲應力較大而進入塑性，因此可以用彈性狀態下翹曲計算的應力計算方法求解極限狀態下的翹曲應力。

根據前文所述計算步驟，運用VB 軟件編寫半潛平臺簡化截面翹曲應力計算程序并計算其極限狀態下板格的翹曲應力，有限元與程序計算所得翹曲應力（S11）值對比見圖7，其中有限元結果用實線表示，程序結果用虛線表示。因破壞始終發生在模型兩端的邊跨，文中所列應力值均為邊跨翹曲應力值。由圖7可知：

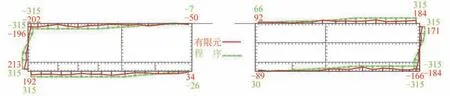
圖7 極限狀態翹曲應力對比Fig.7 The comparison diagrams of the calculated warping stress simplified as open section

1）該半潛平臺的翹曲應力理論計算與有限元結果分布相似，吻合較好，翹曲應力呈反對稱分布。翹曲應力分布位置與趨勢均與有限元結果吻合較好，但部分位置翹曲應力程序計算值偏大。

2）扭轉極限狀態時，4個角點處板格進入塑性，翹曲應力計算時，所取板格已達到其屈服強度。

3 計及翹曲應力的半潛平臺約束扭轉極限強度簡化計算方法

在文獻［20］的基礎上，進一步提出了基于一跨模型并考慮翹曲應力影響的半潛平臺約束扭轉極限強度計算的簡化增量迭代方法。

3.1 理論方法分析及簡化

具體步驟如下：

1）將半潛平臺簡化為長度等于平臺立柱間長度的薄壁梁，根據2.1節所提翹曲應力簡化計算方法，計算半潛平臺剖面上各點的翹曲應力值，外扭矩初值為Tk-1=1 N·m（k=1）。

2）將半潛平臺的加筋板視為一系列相互獨立的四邊簡支的板格單元，假設半潛平臺橫截面上各點轉角相同，橫截面上各點剪應變與該點到截面形心的距離成正比，在扭矩作用下，橫截面上所有板格單元的剪流對截面形心的力矩與截面所受扭矩方向相同，如圖8所示。

圖8 約束扭轉極限狀態時截面的剪力分布Fig.8 Shear force distribution of thin-walled structures in restrained torsional limit state

3）按照文獻［20］，采用約束扭轉極限強度的逐步迭代計算方法，計算各板格單元的剪應變和剪應力，再合成為考慮翹曲應力后的半潛平臺扭轉極限承載力Tk。在迭代過程中，板格臨界剪應力τc根據作用在板格上的翹曲應力σω按式（5）、（6）計算。

式中：σω為作用在板格上的翹曲應力，按式（4）計算，N/mm2；σcr為板格單向受壓的極限正應力，τcr為僅剪力作用下板格的極限剪應力，N/mm2，兩者依據規范［24］計算；β為柔度系數，詳見式（7）。

3.2 半潛平臺約束扭轉極限強度計算結果對比

按3.1 計算步驟編寫了基于一跨模型并考慮翹曲應力影響的半潛平臺約束扭轉極限強度計算程序，計算該半潛平臺的約束扭轉極限強度，與有限元（FEM）結果對比如表5所示。

表5 半潛平臺扭轉極限強度與計算時間Tab.5 The torsional ultimate strength and calculation time of semi-submersible platforms

由表5和圖9可知：

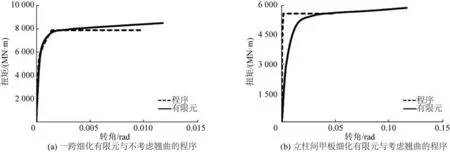
圖9 縱扭工況下平臺扭矩與轉角曲線變化Fig.9 Torque-rotation angle curves under torsion conditions

1）隨著模型長度的增加，有限元扭轉極限承載能力在不斷降低，立柱間甲板的有限元極限扭矩為一跨極限扭矩的69%；其程序的極限扭矩為一跨程序極限扭矩的71%。

2）這里所提考慮翹曲應力影響的半潛平臺扭轉極限強度的計算方法與有限元結果誤差在10%以內；能較為準確地反映隨著長度的增加，半潛平臺扭轉極限承載能力不斷下降的現象，且計算精度較高。

3）由圖9（b）可以看出程序的曲線斜率比有限元的大，這是由于程序是基于一跨模型提出約束扭轉極限強度計算方法，只考慮了翹曲應力對極限強度的影響，但并未考慮模型剛度。

4）由表5可知，一跨模型與兩立柱間平臺模型的程序計算結果均略小于相應的有限元模型計算結果，這是由于簡化計算方法的臨界應力采用的規范公式略微保守。此外，通過對比程序與有限元的計算時間可知，該簡化增量迭代方法可大大減少計算扭轉極限強度的時間，再加上兩立柱間平臺有限元建模時間遠遠大于文中的一跨簡化迭代模型，因此可見，這里所提方法，具有較高的精度和效率。

4 結 語

1）半潛平臺的抗扭剛度主要由橫撐與甲板平臺提供，其中以甲板平臺為主。對比有限元結果可知單元大小與橫撐對半潛平臺約束扭轉極限承載力的影響不大，橫撐僅占11%左右，半潛平臺約束扭轉極限承載力隨模型長度的增加而下降。

2）這里提出的橫撐理論計算方法能較好地反映橫撐能為半潛平臺提供的約束扭轉承載力，其值與有限元結果相差約為3%，可用來估算橫撐對半潛平臺縱扭極限承載力的影響狀況。

3）半潛平臺受約束扭轉時，橫截面的翹曲應力分布規律為4個角點附近板格翹曲應力值較大，翹曲應力呈現反對稱分布；翹曲應力沿長度方向呈現加載兩端大、中間截面小的趨勢，破壞主要發生在加載兩端。

4）在極限狀態時，所提翹曲應力簡化計算結果以及考慮翹曲應力影響的半潛平臺扭轉極限強度的理論計算結果，與有限元結果均吻合較好，能有效計算半潛平臺約束扭轉時的翹曲應力，并能較準確地反映翹曲應力對半潛平臺扭轉極限承載能力的影響。