海溝影響下深水海洋管線成環行為研究

賈紀川，顧繼俊，黃 俊，高 磊，，陳磊磊

（1.中國石油大學（北京） 機械與儲運工程學院，北京 102249；2.中海油研究總院有限責任公司，北京 100028）

立管、電纜和系泊纜是海洋石油管線系統的重要組成部分。研究表明，在安裝和在位運行過程中，由于制造工藝的偏差、上部浮體的運動以及海洋環境的影響，海洋管線可能存在不均勻的扭矩分布，從而造成扭轉失穩現象的發生，圖1（a）所示為典型的海洋柔性立管扭轉現象［1］。在海洋管線的扭轉行為中，一種較為極端的情況是“成環”。在張力和扭矩的共同作用下，海洋管線系統可能出現局部成環現象，當管線所受的張力增大時，環的半徑會相應減小，從而進一步形成扭結，如圖1（b）所示，為實際工程中柔性立管的打結現象［2］。

圖1 立管典型扭轉行為Fig.1 The typical torsional behavior characteristics of a riser

試驗測試和數值計算是分析海洋管線成環行為的主要方式。試驗測試方面：Vachon［3］使用豎直放置的鋼纜樣品完成了扭結形成試驗，以分析海上系泊纜的成環特性；Liu 和Center［4］在試驗中將電纜樣品垂直懸掛在鋼架下，同時施加扭矩和張力，使其成環，并分析了管線成環狀態與管線自身力學特性之間的關系；Yabuta 等［5］和Yabuta［6］使用小直徑的光纖作為試驗測試樣本，以研究不同位移模式下的電纜環“打開”現象，并分析了電纜環保持穩定性的條件；Goss［7］和Goss等［8］將小段鎳鈦諾桿夾持在水平加載裝置上，通過扭轉桿端和調整桿的松弛度以模擬環的形成，并分析了不同輸入扭矩、松弛度以及自身重力等因素對樣品成環行為的影響。

數值計算方面：Zajac［9］和Rosenthal［10］基于彈性理論研究了電纜形成環或者扭結的臨界載荷；Knapp［11-13］基于能量法建立了理論方程，以分析筆直的電纜在拉伸和扭轉共同作用下的響應，對應的計算程序則可以有效處理一端自由或兩端固定的電纜扭轉成環問題；Goyal等［14-15］、Goyal和Perkins［16-17］基于基爾霍夫桿理論建立了動態數值模型，以捕捉管線不同狀態之間的動態轉換過程，并指出了該理論在海洋管線扭轉行為和DNA 超螺旋狀態研究中的應用前景，隨后在此基礎上提出了一種包含12階桿單元模型和6階桿單元模型的桿—懸鏈線混合模型，以有效分析船用海纜的動態彎曲和扭轉行為，與傳統的懸鏈線模型相比，該混合模型的計算效率提高了1.5～2.0倍；Neto等［18-20］、Neto和De arruda matrins［21］、Neto［22］提出了一個精確的非線性三維動態梁單元模型，并基于該模型對海洋立管成環過程中涉及的扭轉穩定性、管線自接觸、海流作用及管土摩擦等問題均做了深入研究；Zhang 等［2］使用OrcaFlex 軟件研究了在扭轉、拉伸等外部載荷共同作用下海洋立管的成環機理，并完成了相關的可靠性分析。

對于前述研究，從研究對象的角度看，由于試驗條件的限制，試驗測試通常以直桿或者直纜作為海洋管線成環研究的試驗樣本；而數值計算的研究對象相對廣泛，包括電纜、系泊纜和海洋立管。從研究內容的角度看，無論是試驗測試還是數值計算，前人的研究主要集中在成環的機理上，對于環境因素對海洋管線成環的影響研究較少。Goyal 等［14］、Neto 等［18］和Zhang 等［2］均指出海洋管線的成環區域位于其觸地區附近，而該部分區域恰是海溝易形成的區域［23-25］。因此下文采用海洋工程有限元分析軟件OrcaFlex，就海溝對立管成環的影響開展相關研究，主要分析海溝輪廓、海溝位置及海溝土壤屬性對成環過程中立管相關力學特性的影響，并考慮了立管成環過程中臨界載荷的變化。

1 力學模型

1.1 管線模型

使用有限元軟件OrcaFlex框架下的管線模型［26］來建立研究所需的基本海洋立管模型。

管線模型基于集中質量法建立，由多個單元組成，單元之間通過末端的節點連接。每個單元的質量為0，并等效于由彈簧阻尼器連接的2個彈性桿，以此模擬管線模型的軸向拉伸、壓縮和扭轉特性。

OrcaFlex 框架下的管線模型如圖2 所示。模型中每個節點的質量為與其相連的2 個單元質量總和的一半，管線模型2個末端節點除外，其質量為與之相連的單個單元質量的一半。組成管線模型的單元所受的重力、浮力、水流力以及海床作用力均集中分配到各個單元節點上。

圖2 OrcaFlex管線模型Fig.2 The pipeline model in OrcaFlex

管線的平衡方程為［27］：

式中：R是關于位置變量x、y、z和時間變量t的矢量函數；m是管線模型的單元質量；Te是有效張力［28］；s?是管線單元變形后的長度；V是分布載荷；wf是模型單元所受的浮力；weh是單元所受的水流力；wg是單元所受的重力；wsd是單元所受的海床土反力；M是截面彎矩［28］。

1.2 管土作用模型

OrcaFlex 中引入了4 種模式以表征海洋管線與海床之間在垂直方向上的相互作用過程，包括未接觸模式、初次貫入模式、抬升模式和再貫入模式［29］。

圖3展示了當貫入深度z值改變時，海床土阻力P（z）的變化。管線初步接觸海床，采用初次貫入模式計算土阻力。

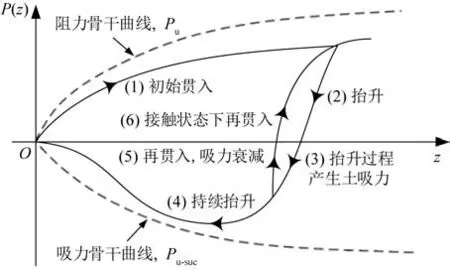
圖3 管土作用曲線Fig.3 Pipe-soil interaction curve

隨著貫入深度的增加，土阻力逐漸接近極限土阻力Pu。隨后，管線開始抬升，此過程采用抬升模式進行計算。在抬升過程中，土阻力的值逐漸降低，而土吸力Pu-suc的值開始增加。當抬升距離達到一定程度時，土吸力接近其極限值。當土吸力達到極限值后，若抬升過程繼續，則土吸力開始減小并將最終降至0；另一種情況則是抬升過程在土吸力達到極限值后終止，管線開始再次貫入海床，此時模式轉變為再貫入模式。在再貫入模式中，隨著貫入深度的增加，土吸力值開始減小，而土阻力值Pu（z）開始再次增加，并最終接近極限土阻力。抬升和再貫入過程的往復循環，將導致管線在海床上的貫入深度逐漸增加。

土阻力和吸力方程：

式中：Pu（z）為海床土阻力；Nc（z/D）為承載因子；D為管線直徑，Su（z）為土壤剪切強度；Su0為海床表面不排水抗剪強度；r為抗剪強度梯度；Pu-suc為土吸力；fsuc為吸力因子。

采用修正的庫侖摩擦模型對水平方向上的管線—土壤相互作用過程建模。海床土壤對管線施加的水平力如圖4所示。如果水平力小于克服土壤摩擦的最小力，則假定土壤為線彈性，水平力和管線位移之間的關系如下：

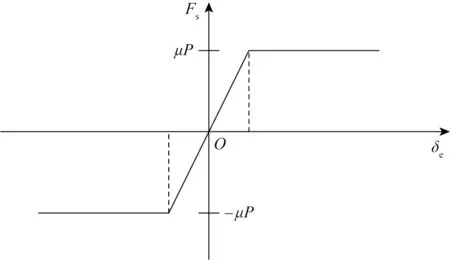
圖4 管土作用庫倫摩擦模型Fig.4 The Coulomb friction model for pipe-soil interactions

式中：Ks是土壤的水平剛度；δe是土壤的橫向變形。

如果水平力大于克服土壤摩擦的最小力，則假定水平方向上的土壤作用力為摩擦力，該摩擦力與垂直方向上的海床土反力成正比，關系表達式為：

式中：μ是摩擦因數；P是垂直方向上的海床土反力。

1.3 海溝模型

海溝是由立管和海床土壤之間的相互作用形成的，海溝的存在會顯著影響觸地區立管段的性能［23-25］。研究采用經驗公式構建海溝輪廓，并分析其對立管成環的影響。Wang和Low［24］提出了一種參數公式來描述海溝的輪廓，婁敏等［25］則對該參數公式進行了改進，使其能夠更準確地描繪海溝剖面。研究采用了婁敏等［25］提出的經驗公式，以生成不同長度和深度的海溝模型。

構建海溝模型如圖5所示。參考點（RTDP）指平坦海床上立管的觸地點。隨著海溝的延伸和擴展，立管在海溝內的觸地點（TDP）會沿著海溝的左側(以海溝最大深度點為分界點，靠近海溝起始點的一側)移動。ΔTP表示RTDP 與海溝起始點（TBP）之間的距離；LT表示點TBP 與海溝終止點（TEP）之間的水平距離，即海溝的長度；dmax表示海溝的最大深度；Lmax表示TBP和海溝最深點（TMP）之間的水平距離。

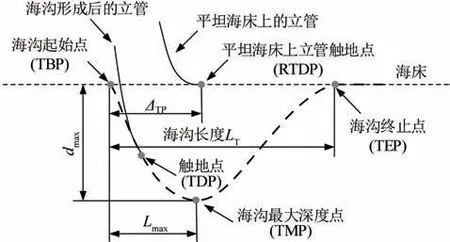
圖5 典型海溝輪廓示意Fig.5 A sketch of a typical trench profile

構建海溝模型的3個主要參數分別是LT、dmax和ΔTP，其中LT和dmax確定海溝的基本尺寸，ΔTP確定海溝的位置。LT和dmax的值基于婁敏等［25］提出的經驗公式獲得：

其中，

式中：Rd、Rm、RHV、RL和RTP均為無量綱參數；D是立管外徑；m是立管單位長度的質量；ρ是海水密度；H是立管頂部懸掛點（HOP）和RTDP 之間的水平距離；V是HOP 和RTDP 之間的垂直距離。D、m、ρ和V的值見表1 和表2。H的值在OrcaFlex 中通過靜力計算獲得，為303 m。將式（9）代入式（7）和（8），可得到RL和RTP的值，再將RL和RTP的值代入式（10），可得到LT和ΔTP的值，至此確定了海溝的位置和長度。

表1 立管參數Tab.1 Riser parameters

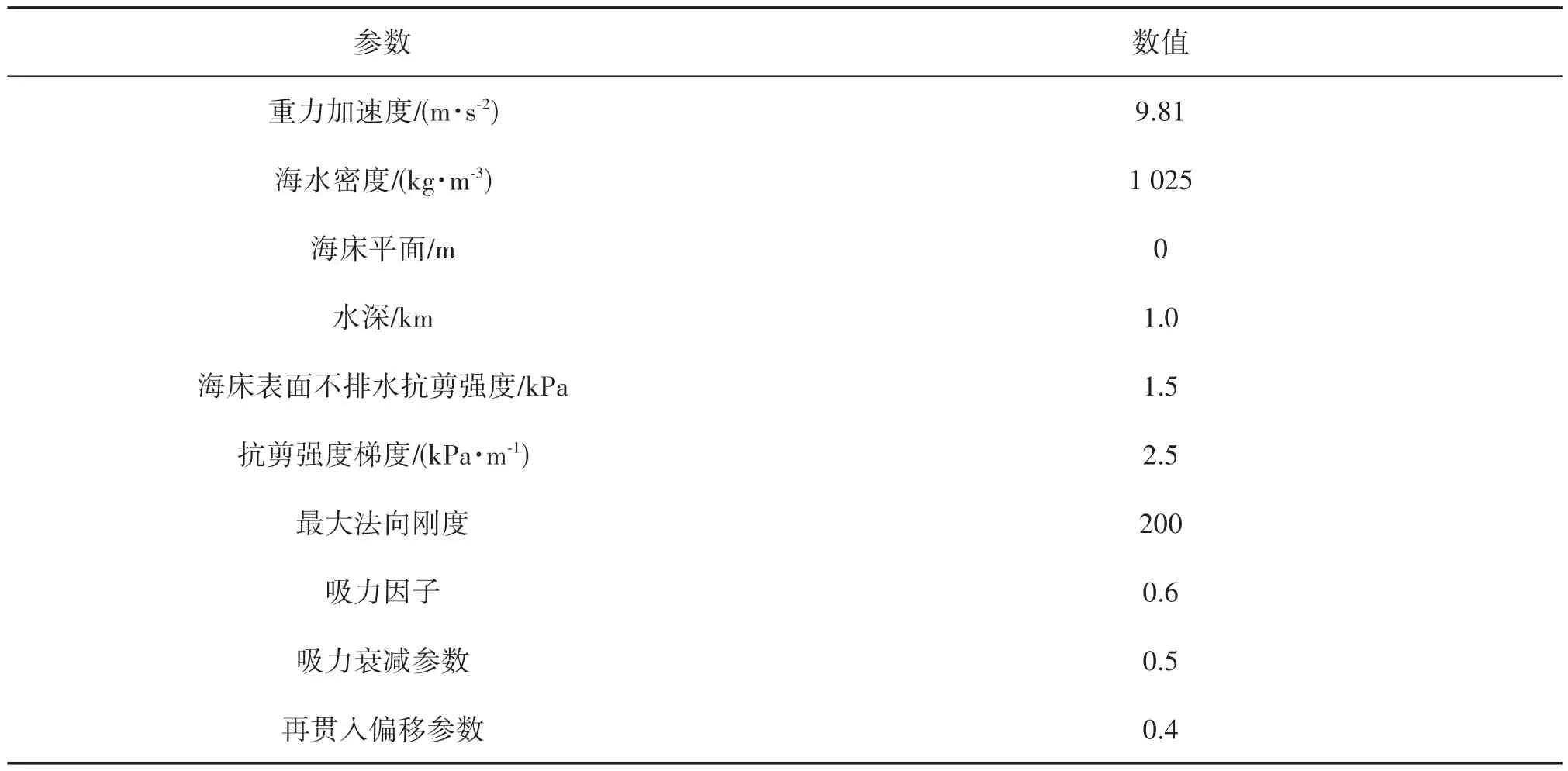
表2 環境參數Tab.2 Environmental parameters

海溝基本形狀的構建是參考Aubeny和Biscontin［30］提出的三次多項式：

2 成環參數分析

2.1 立管成環屬性

參考Neto等［19］和Zhang等［2］的參數設置，選擇深水海洋管線中較為常見的鋼懸鏈線立管作為研究對象，立管的幾何與材料參數如表1所示。

在環境參數中，為貼近實際工況，選擇非線性海床模型作為研究模型，涉及海床表面不排水抗剪強度、抗剪強度梯度和吸力因子等非線性土壤參數的設定，所有環境參數如表2所示［19，24］。

為了便于分析海溝上的立管成環行為，參考Neto 等［18］研究中提出的施加載荷方式，在立管的頂點緩慢加載線性扭矩，如圖6所示。

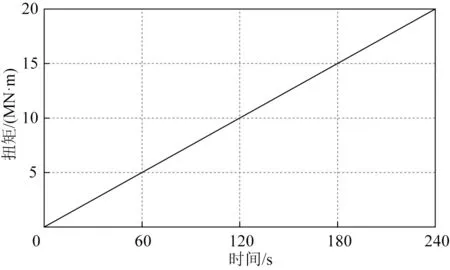
圖6 在立管頂點線性施加扭矩Fig.6 The linearly applied torque at HOP

研究以Neto等［20］提出的“自接觸狀態”作為立管成環的極限狀態，此時立管環為完整的閉環。在平坦海床上，成環的立管與懸鏈線狀態下的立管對比如圖7所示。重點對比了2種狀態下立管的整體形態、軸向應力分布和曲率分布，軸向應力基于規范《DNV-RP-F204》［31］計算得到，計算公式為：

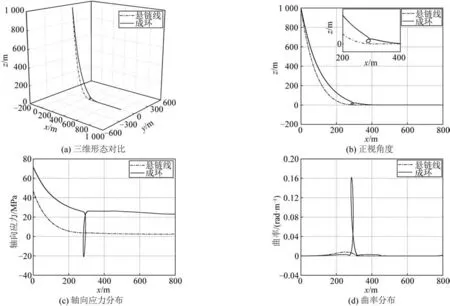
圖7 立管懸鏈線狀態和成環狀態對比Fig.7 Comparison between catenary state and loop formation state of riser

式中：σa表示軸向應力；Te表示有效張力；D表示立管外徑；t表示立管壁厚。

在轉驅時機優化中，主要考慮轉驅時的油藏壓力和井間的熱連通性。在蒸汽吞吐中，第2周期到第4周期加熱半徑和加熱區域不斷擴大，到第4周期，井間已經建立起熱連通。第5周期，其加熱區域擴大較為緩慢，主要起到重復加熱地層的作用。綜合考慮蒸汽驅階段油汽比、采收率和凈采油量等因素，推薦在蒸汽吞吐4周期以后轉驅，采收率可達27.1%。

在圖7（a）中，當立管形成環時，成環處的立管段在x、y、z三個坐標軸方向上均存在一定偏移距離。從正視角度，基于圖7（b）及其局部放大圖可以發現，成環的位置位于懸鏈線立管的觸地區附近。隨著立管環的形成，沿立管分布的軸向應力整體變大，最大軸向應力位于立管懸掛點處，如圖7（c）所示。通過對比圖7（b）和圖7（c）可以發現，在立管成環位置處軸向應力出現負值，說明存在局部壓縮，最大壓縮力可通過該點有效張力的絕對值體現。在圖7（d）中，當立管環形成時，沿立管的曲率分布與懸鏈線狀態下大致相似，不同之處在于成環位置處會出現曲率的極值，說明此處彎曲程度最大，在參數分析中可通過最大彎矩體現。

2.2 海溝輪廓的影響

基于1.3節構建海溝輪廓的經驗公式，在OrcaFlex中建立深度為0.5D到5.5D的海溝模型，海溝系統的原點與圖7 系統的原點保持一致，且后文海溝系統的建立均遵循這一規則。不同深度海溝如圖8 所示。分析隨著管土作用的持續進行，海溝輪廓的擴展對立管成環行為的影響。

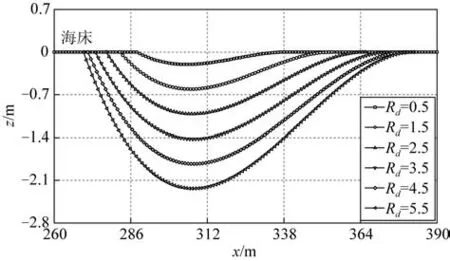
圖8 不同長度和深度的海溝Fig.8 Trenches at varied lengths and depths

圖9展示了不同海溝輪廓對立管成環行為的影響。如圖9（a）所示，隨著海溝深度和長度的增加，立管環的位置呈現下沉趨勢。從俯視角度，環的開度也隨著海溝的擴展而增加，如圖9（b）所示。分析原因為：隨著海溝的擴展，其深度和長度增加，立管位于海溝上方的懸空段逐漸變長，失去了海床土反力的支持，在自身重力的作用下，立管環將呈現下沉趨勢；隨著環的下沉，立管張緊，立管環將逐漸脫離自接觸狀態，導致環路的打開。

圖9 不同海溝輪廓對立管成環的影響Fig.9 The influence of varied trench profiles on the riser loop formation

隨著立管環脫離自接觸狀態，由立管成環導致的局部壓縮逐漸減小，壓縮力的最大值呈現下降趨勢，如圖9（c）所示；與之相對應，立管的局部彎曲程度也會有所降低，最大彎矩值同樣呈現下降趨勢，如圖9（d）所示。

2.3 海溝與立管環相對位置的影響

以深度是3.0D的海溝為基礎，調整海溝起始點坐標為275、271、267、263、259和255 m，分別對應圖10中的位置1 到位置6，研究立管在海溝不同位置處成環時力學屬性的變化。其中在位置6 時，立管環處于海溝最深點正上方。

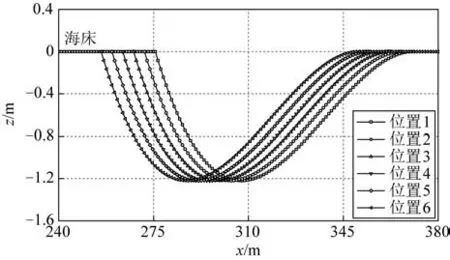
圖10 不同海溝位置Fig.10 Trenches at various locations

圖11展示了當立管環處于不同的海溝位置時，立管力學屬性的變化。從圖11（a）和11（b）可以看出：隨著立管環從海溝的邊緣地帶向最深點平移，其開度逐漸減小，當到達海溝最深點正上方時，立管已形成完整閉環。原因在于：隨著立管環的位置向海溝最深點正上方靠近，環兩側懸空的立管段的長度差值逐漸減小，與之對應的，是兩側施加在立管環上的拉力差值的減小，從而使其更易達到平衡狀態；相對而言，在海溝邊緣處，立管環承受單側懸空管段的影響，更易呈現“打開”狀態。

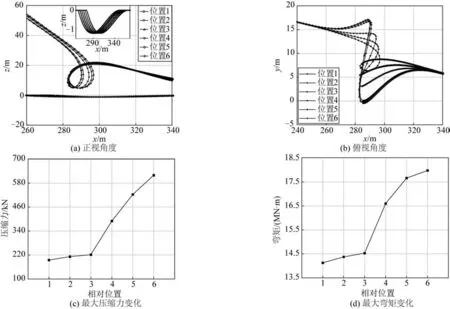
圖11 不同位置海溝對立管成環的影響Fig.11 Influence of various trenches at different locations on the riser loop formation

隨著立管環向海溝最深點的正上方靠近，立管逐漸達到自接觸狀態，與之對應的是立管成環處，最大壓縮力和最大彎矩的逐步增大，如圖11（c）和11（d）所示。

2.4 海溝土壤屬性的影響

如圖7（a）所示，立管在成環過程中既有平移運動也有抬升運動，平移運動涉及立管與海床表層土壤之間的摩擦，抬升過程中立管則可能受到土吸力的影響。因此本節基于上述2個方面，選擇非線性土壤參數中的海床表面不排水抗剪強度Su0和吸力因子fsuc作為研究參數，分析其對海溝上立管成環行為的影響。以深度是3.0D的海溝模型為基礎，在海溝處，立管環在2 個典型土壤參數影響下的力學性能變化如圖12 和圖13所示。

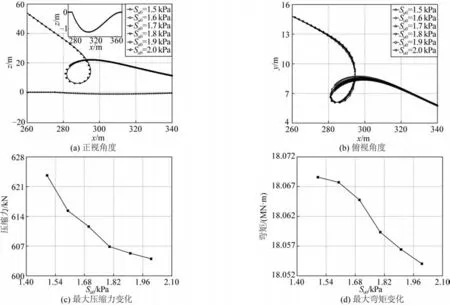
圖12 不同Su0對立管成環的影響Fig.12 Influence of various Su0 on the riser loop formation

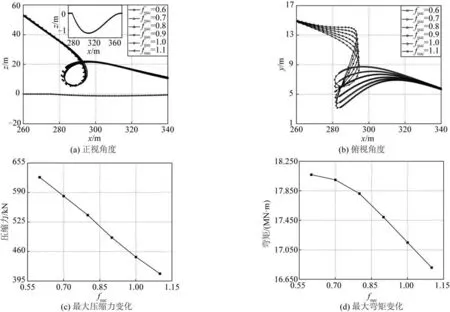
圖13 不同fsuc對立管成環的影響Fig.13 Influence of different fsuc on the riser loop formation

如圖12 所示，隨著Su0的增大，立管環呈不明顯的打開趨勢，與之對應的是壓縮力和彎矩的最大值均呈現下降趨勢。

Su0是表征海床剛度的關鍵參數［32］，Wang等［33］指出較高的抗剪強度對應較硬的海床。Chen等［34］則發現，較高的Su0值對應較大的海床土阻力。因此，結合第1.2 節中的式（6）可知，Su0的增大將導致垂直方向上海床施加給立管的土反力增大，即式（6）中的P值增大，從而導致立管受到的海床土壤摩擦力Fs增大，使得立管環在向自接觸狀態轉化的過程中，在水平運動方向上受到更大的阻力。因此，隨著Su0的增大，立管環的開度會增大，與之對應的是最大壓縮力和最大彎矩的減小，如圖12（c）和12（d）所示。

圖13 展示了不同吸力因子fsuc對立管成環的影響。與Su0類似，隨著fsuc的增大，立管環逐漸打開，壓縮力和彎矩的最大值均呈現下降趨勢。通過對比立管環力學屬性的變化范圍可以發現，在增長速率相同的情況下，fsuc對立管成環的影響程度大于Su0。

在立管環形成的過程中，立管整體呈現抬升趨勢。Wang 等［33］指出，當立管開始向上運動時，土壤對立管的作用力將轉化為土吸力。Shiri［35］則通過研究證明土吸力的大小主要由吸力因子fsuc決定，較大的fsuc對應較強的土吸力［36］。因此可以推斷，在立管成環過程中，隨著fsuc的增大，立管所承受的土吸力增大，立管環向自接觸狀態轉化的過程受到阻礙，從而導致立管環開度的增加及相應力學屬性的變化。

3 臨界載荷

Neto等［19］通過監測立管端部的旋轉角度并繪制扭矩—轉角曲線圖來初步判斷立管成環過程的穩定性，這里參考該方法，在立管頂點線性施加扭矩的情況下，實時監測立管頂點的旋轉角度。由于fsuc對立管成環行為的影響相對較大，本節選取不同的fsuc值，分析不同工況下立管成環的臨界載荷。

圖14 所示為不同fsuc對應的扭矩—頂部轉角曲線圖。隨著旋轉角度的增大，在立管頂部施加的扭矩呈現迅速增加—緩慢增長—逐漸穩定的變化趨勢。通過對比發現，當旋轉角度達到368°時，施加的扭矩基本達到臨界狀態并保持穩定，此時立管在觸地區基本形成完整的閉環。圖14 中的局部放大圖以及表3 顯示，隨著fsuc的增大，立管成環的臨界扭矩也會增大。此外，圖14 還顯示，盡管不同fsuc作用下立管成環的臨界扭矩有所不同，但扭矩從迅速增加狀態到緩慢增長狀態的轉折點卻基本一致，該點對應的頂部旋轉角度為45°，扭矩為9.4 MN·m。

表3 立管成環的臨界扭矩對比Tab.3 Comparison of critical torque of riser loop formation

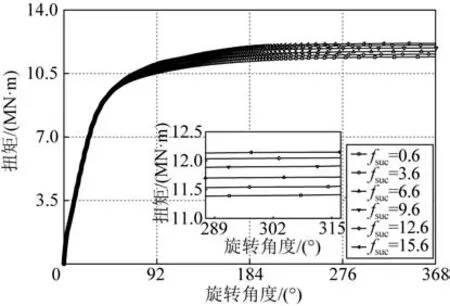
圖14 扭矩隨立管頂部旋轉角度的變化Fig.14 Variation of torque with increasing rotation angle at HOP

除臨界扭矩之外，由于立管頂部的旋轉角度會直接影響立管成環的進程，因此有必要分析不同fsuc對立管頂部旋轉角度的影響。以fsuc=0.6時的臨界扭矩11.425 0 MN·m為基準，對比施加相同扭矩時，不同fsuc作用下立管成環的旋轉角度。圖15和表4顯示：對立管施加相同扭矩時，隨著fsuc的增大，立管頂部旋轉角度呈現下降趨勢。說明fsuc的增長不僅會提高立管成環的臨界扭矩值，在施加相同扭矩的情況下，fsuc數值的增大還會減小立管頂部的旋轉角度，從而降低成環速率。

表4 施加相同扭矩時旋轉角度對比Tab.4 Comparison of rotation angles when applying the same torque

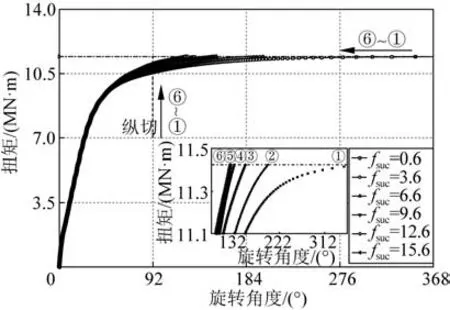
圖15 相同扭矩下的旋轉角度Fig.15 Rotation angles at the same torque

4 結 語

基于管線集中質量模型、非線性土壤模型和海溝經驗模型，在OrcaFlex框架下建立了海溝作用下的深水懸鏈線立管成環模型，研究了立管成環的基本特性和海溝對立管成環行為的影響，并分析了立管成環的臨界載荷。具體結論如下：

1） 在頂部扭矩和非線性海床的共同作用下，立管可能在其觸地區成環。當立管環達到自接觸狀態時，在立管的成環處會出現壓縮力和彎矩的極值。

2） 海溝的延伸擴展、海溝的位置以及海溝的土壤屬性均對立管的成環行為存在規律性的影響。其中，海溝深度和長度的增加，立管環從海溝最深點向海溝邊緣的平移，以及海溝土壤參數Su0和fsuc的增大，均可提升立管環的開度，降低立管成環過程中的最大壓縮力和最大彎矩，從而減少成環行為帶來的損傷。

3） 扭矩—頂部轉角關系的研究表明，隨著立管頂部旋轉角度的增大，所施加的扭矩呈現迅速增加—緩慢增長—逐漸穩定的變化趨勢，fsuc數值的增大將導致立管成環臨界扭矩的增加和成環速率的降低，但外部扭矩從迅速增加狀態到緩慢增長狀態的轉折點是基本一致的。

研究表明：合理的海溝輪廓、海溝位置和海溝土壤屬性可有效降低立管成環帶來的損傷，并可通過預測臨界載荷避免完整立管環的形成。研究成果可以為非線性海床上海洋管線扭轉成環問題的相關研究提供參考。