改進GWO算法求解柔性作業(yè)車間調(diào)度問題
馬隨東,艾爾肯·亥木都拉,鄭威強
(新疆大學(xué)機械工程學(xué)院,新疆烏魯木齊 830017)
0 前言
車間調(diào)度任務(wù)的基本目的是根據(jù)不同客戶的訂單在截止日期內(nèi)完成指定生產(chǎn)任務(wù)的活動。柔性作業(yè)車間調(diào)度問題(Flexible Job Shop Scheduling Problem,F(xiàn)JSP)廣泛存在于人類生產(chǎn)活動的各個領(lǐng)域,如紡織制造、半導(dǎo)體制造、汽車裝配以及化學(xué)材料加工等。FJSP由機器分配和操作排序2個子問題組成,機器分配解決每個操作的候選集中機器選擇問題,操作排序是調(diào)整每個機器上的所有操作,使得完成所有操作的最大完工時間最小。眾所周知FJSP是NP難問題,求解該問題可以采用精確方法和近似方法,由于NP難問題的復(fù)雜性,精確方法在復(fù)雜FJSP上不適用,近似方法是目前研究FJSP的主流方法。
國內(nèi)外學(xué)者利用近似算法對FJSP的應(yīng)用進行了大量研究。在進化算法(Evolutionary Algorithms,EA)方面,學(xué)者們根據(jù)FJSP的特點對編碼、初始種群、選擇、交叉以及變異進行了大量研究,很多研究還將局部搜索算法嵌入EA,加強了EA算法的局部開發(fā)能力[1-2]。在群體智能算法(SI)方面。姜飛等人[3]以最大完工時間和客戶滿意度為目標(biāo),通過灰狼優(yōu)化算法對多目標(biāo)柔性作業(yè)車間動態(tài)調(diào)度問題進行了研究。姚遠遠、葉春明[4]以最小化最大完工時間為目標(biāo),通過改進混合灰狼算法對作業(yè)車間調(diào)度問題進行了研究,與布谷鳥搜索算法進行對比,驗證了改進GWO求解作業(yè)車間調(diào)度問題的有效性。吳繼浩、楊濤[5]結(jié)合改進GWO算法與模擬退火算法對FJSP進行了研究。姜天華[6]以最小制造時間為目標(biāo)對JSP和FJSP設(shè)計了離散GWO算法。由于FJSP的本質(zhì)是離散的,故對FJSP應(yīng)用GWO之前要實現(xiàn)灰狼個體位置的離散性和多樣性。
考慮到GWO與局部搜索算法集成的便利性,本文作者首先采用機器和工序的雙層編碼策略,并設(shè)計種群初始化方案;其次評估初始種群質(zhì)量,并進行精英保留和錦標(biāo)賽選擇;接著為了尋找操作序列的最優(yōu)順序,對操作序列設(shè)計了GWO鄰域搜索;然后對生成的最優(yōu)序列執(zhí)行TS搜索。此外,為了搜索種群中最優(yōu)灰狼個體位置周圍的搜索空間,對灰狼個體位置設(shè)計了變異操作。最后通過基準(zhǔn)實例的仿真實驗,評估改進GWO算法求解FJSP的性能。
1 模型建立
目前FJSP公認的數(shù)學(xué)模型是存在一組作業(yè)J={J1,…,Jn}和若干機器M={M1,…,Mm},每個作業(yè)有若干操作,即Ji={Oi,j,…,Oi,ni},其中ni是Ji的操作總數(shù),每個操作都有對應(yīng)的機器子集Mi,j?M,問題要求是將所有操作分配到對應(yīng)機器上且要保證每臺機器上的操作序列是最優(yōu)的,即保證所有作業(yè)的最大完工時間最小min(Cmax)。
2 灰狼優(yōu)化器原理
灰狼優(yōu)化器原理如圖1所示。α、β、δ狼稱為領(lǐng)導(dǎo)者,ω狼稱為進攻者,一個灰狼個體代表了一個可行的調(diào)度方案,位于金字塔頂端的α狼代表最優(yōu)調(diào)度方案。當(dāng)初始種群確定后,按照灰狼個體的最大制造跨度將所有灰狼個體進行排列,以確定最好的領(lǐng)導(dǎo)者和攻擊者,GWO的搜索行為由領(lǐng)導(dǎo)者進行引導(dǎo)。灰狼算法搜索過程可分為圍捕、狩獵和攻擊3個階段。
圖1 灰狼領(lǐng)導(dǎo)層級
2.1 圍捕
圍捕階段,由式(1)(2)完成對獵物的包圍。
Dp=|C·Xp(t)-X(t)|
(1)
X(t+1)=Xp(t)-A·Dp
(2)
式中:t為迭代次數(shù);Xp為獵物位置;X為ω狼的位置;Dp為獵物與ω狼之間的絕對距離;A和C是系數(shù)向量,由式(3)(4)確定。
A=2ar1-a
(3)
C=2r2
(4)
式中:r1、r2∈rand(0,1)是隨機向量;a是收斂系數(shù),從2逐漸下降到0,由式(5)確定。
(5)
式中:a1=2和a2=0為收斂系數(shù)的初始值和終止值;n為遞減系數(shù),n=1-t/tmax。
2.2 狩獵
在狩獵階段,由于獵物位置(最優(yōu)解)未知,故領(lǐng)導(dǎo)狼需預(yù)測獵物的潛在位置,而進攻狼根據(jù)領(lǐng)導(dǎo)狼的位置進行調(diào)整,以便攻擊獵物。式(6)—(8)描述如下:
(6)
X1=Xα-A1·Dα
X2=Xβ-A2·Dβ
X3=Xδ-A3·Dδ
(7)
(8)
2.3 攻擊
灰狼是否對獵物發(fā)動攻擊由收斂系數(shù)A決定,當(dāng)|A|≥1時,灰狼與獵物疏遠進行全局搜索;當(dāng)|A|<1時,灰狼接近獵物完成獵殺任務(wù)。
3 改進GWO算法的實現(xiàn)
由于GWO算法求解FJSP時會很快陷入局部最優(yōu),故將禁忌搜索算法(Tabu Search,TS)嵌入到GWO算法中,以輔助GWO算法跳出局部最優(yōu)。所提GWO算法工作流程如圖2所示。

圖2 GWO算法的工作流程
3.1 編碼與解碼
由于編碼策略不僅影響算法各部分的連接和解碼效率,而且對GWO與局部搜素算法的集成至關(guān)重要。因此采用機器分配和操作排序雙層編碼策略,將作業(yè)、機器和加工時間一一對應(yīng)。首先在區(qū)間[-n,n]內(nèi)生成一個由實數(shù)組成的灰狼位置向量,向量中的元素符合均勻分布,且該向量與作業(yè)操作數(shù)量的長度相等,其中n表示作業(yè)數(shù)量,接著利用ROV規(guī)則將灰狼位置向量中的元素轉(zhuǎn)換為對應(yīng)的操作序列,圖3所示為轉(zhuǎn)換之后的操作序列:1→3→3→2→1→2→3→1→2。序列中相同數(shù)字出現(xiàn)的次數(shù)表示作業(yè)的第幾次操作。如序列中第一個1代表第一個作業(yè)第一個操作O11,第二個1代表第一個作業(yè)第二個操作O12,其余作業(yè)操作依次類推。然后根據(jù)每個操作的可選機器集長度為每個操作隨機分配一臺機器。
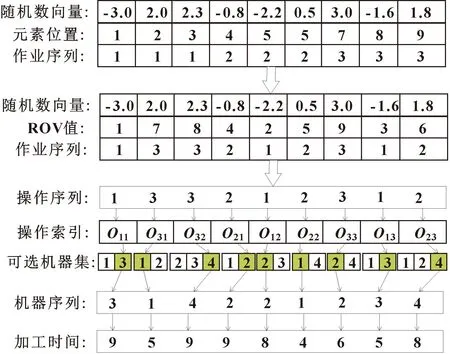
圖3 編碼策略
3.2 種群初始化
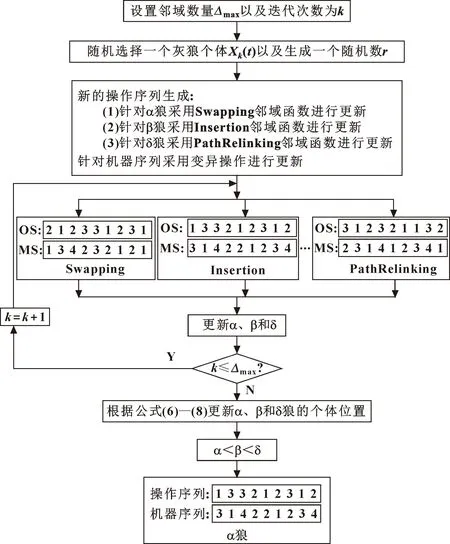
根據(jù)第3.1節(jié)獲得的機器序列和操作序列生成初始種群,方法如下:在機器分配階段,首先依據(jù)操作Oi,j的加工條件,在可選機器集中為操作Oi,j選擇加工時間最短的機器M1和可行時間最早的機器M2,分別計算操作Oi,j在機器M1和M2上的完成時間T1和T2,若T1 應(yīng)用GWO算法求解FJSP的關(guān)鍵是保證GWO算法的全局性和多樣性。故針對操作序列設(shè)計了交叉鄰域、插入鄰域和路徑重連鄰域3種鄰域函數(shù),鄰域函數(shù)表達式為式(9),所設(shè)計GWO算法鄰域搜索結(jié)構(gòu)如圖4所示。式(9)中Xk表示由鄰域函數(shù)得到第k個灰狼的調(diào)度方案,Insertion函數(shù)定義了對Xβ進行插入鄰域,Swapping函數(shù)定義了對Xα進行交叉鄰域,PathRelinking函數(shù)定義了對Xδ進行路徑重連鄰域,r∈[0,1]是隨機數(shù)。 (9) 圖4 GWO算法鄰域搜索結(jié)構(gòu) GWO算法鄰域搜索步驟如下: 步驟1,設(shè)置迭代次數(shù)k=1和鄰域數(shù)量Δ,令Δ=1,2,…,Δmax,選擇較優(yōu)的灰狼個體Xk(t)。 步驟2,隨機生成一個隨機數(shù)r≤[0,1],執(zhí)行以下程序: (1)若r≤1/3,則執(zhí)行Swapping鄰域產(chǎn)生一個新的調(diào)度方案α。 (2)若1/3 (3)若r>2/3,則執(zhí)行PathRelinking領(lǐng)域產(chǎn)生一個新的調(diào)度方案δ。 步驟3,判斷k≤Δmax是否成立,若條件成立,令k=k+1,則轉(zhuǎn)到步驟2,否則轉(zhuǎn)到步驟4。 步驟4,根據(jù)式(6)—(8)更新α、β和δ狼的個體位置。 步驟5,按照α、β和δ狼的makespan進行排列。 步驟6,輸出最優(yōu)調(diào)度方案α。 3.3.1 交叉鄰域 首先在OS序列中隨機選擇2個不同的位置k1和k2,然后將k1和k2位置上的序列交換,其余序列的位置不變。交叉鄰域如圖5所示。 圖5 交叉鄰域 3.3.2 插入鄰域 首先在OS序列中隨機選擇2個不同的位置k1和k2,若k1 圖6 插入鄰域 3.3.3 路徑重連鄰域 PR鄰域如圖7所示。具體表述如下:首先從初始種群中隨機確定起始解OS和導(dǎo)向解OS′,然后建立路徑解,即比較OS與OS′中第i個位置上的序列是否相等,若相等,則保持OS中第i個位置上的序列不變,否則在OS中找到與OS′序列相等的第j個序列,將OS中第j個序列插入到第i-1個序列的后面,重復(fù)上述過程直到最后一個路徑解與導(dǎo)向解完全一致,最后計算每個路徑解的最大制造跨度,選擇最大制造跨度最小的路徑解作為新的個體。 圖7 PR鄰域 3.3.4 機器變異 根據(jù)操作序列OS的長度,變異位置個數(shù)取OS長度的一半并左取整,接著將所選位置的機器更改為對應(yīng)操作的可選機器集中的其他機器。機器變異如圖8所示。圖8中OS長度為9,變異位置為4,選擇操作O1,1、O2,2、O2,3和O3,2的機器序列進行變異,例如O1,1的可選機器為M1和M3,變異前為M3,變異后為M1。 圖8 機器變異 TS算法[7]從一個可行解出發(fā),通過關(guān)鍵加工路徑的Nopt1鄰域搜索最優(yōu)解[8]。TS的初始調(diào)度方案為α,TS搜索流程如圖9所示,執(zhí)行步驟如下: 圖9 TS搜索流程 步驟1,設(shè)置TS迭代次數(shù)k、s,置禁忌表為空,初始調(diào)度方案為α,禁忌迭代次數(shù)Tn,禁忌閾值Tu。 步驟2,判斷k≥Tn是否成立,若條件成立,則執(zhí)行步驟8,否則執(zhí)行步驟3。 步驟3,獲取α的關(guān)鍵加工路徑上的操作和機器分配,改變關(guān)鍵操作的機器分配生成新鄰域,估計每種鄰域的最佳制造跨度。 步驟4,判斷s≥Tu是否成立,若條件成立,則執(zhí)行步驟5,否則執(zhí)行步驟6。 步驟5,將滿足藐視準(zhǔn)則的候選解作為當(dāng)前解,并執(zhí)行步驟7。 步驟6,判斷候選解的禁忌屬性,選擇鄰域中非禁忌的最佳解作為當(dāng)前解,并執(zhí)行步驟7。 步驟7,更新禁忌列表,轉(zhuǎn)到步驟2。 步驟8,輸出最優(yōu)調(diào)度方案。 在GWO鄰域搜索階段,首先通過Swapping、Inserting和PathRelinking鄰域和機器變異得到操作分配的最優(yōu)方案α,然后對α分配方案進行TS搜索,對于每個Nopt1鄰域要先確定關(guān)鍵加工路徑中的關(guān)鍵操作,調(diào)整這些操作可以有效優(yōu)化makespan。在TS搜索過程中,TS迭代次數(shù)隨著GWO迭代次數(shù)的增加而增加,TS禁忌閾值由關(guān)鍵加工路徑上操作數(shù)量的倍數(shù)組成。 由于當(dāng)前個體的位置更新依賴于最佳狼α、β和δ的位置信息,這種更新機制往往缺失種群多樣性,易使算法早熟收斂。故通過式(10)對最佳領(lǐng)導(dǎo)個體進行變異操作,以使領(lǐng)導(dǎo)個體從自身搜索空間周圍探索新的最優(yōu)解[9]。 (10) 改進GWO算法在Intel(R) Core(TM) i5-6300HQ CPU @2.30 GHz,4 GB RAM的PC上運行,運行系統(tǒng)為Windows10專業(yè)版,代碼在MATLAB2021a上實現(xiàn)。實驗中選擇58個測試實例驗證改進GWO算法的有效性。這些測試基準(zhǔn)分別是Brandimate(1993)的10個實例(MK01-MK10)、Kacem(2002)的5個實例(K01-K05)、Hurink(1994)等的43個實例(mt06、mt10、mt20以及LA01-LA40)。表1為改進GWO算法的參數(shù)設(shè)置。 表1 改進GWO算法參數(shù)設(shè)置 4.1.1 實驗一 表2為改進GWO算法與其他算法在Kacem測試實例上的結(jié)果對比。HA[1]、HGWO[6]、TS[7]、VNSGA[10]、Heuristic[11]、MA[12]、IWOA[13]、GLNSA[14]為對比算法,在以上算法中只有 GLNSA、Heuristic、HGWO以及IWOA算法獲得了Kacem算例的完整解,其中僅有GLNSA算法達到目前已知的最優(yōu)解,改進GWO算法獲得的最優(yōu)解優(yōu)于HGWO,與GLNSA算法的最優(yōu)解相當(dāng),此外改進GWO算法運行時間也優(yōu)于HGWO算法。 表2 Kacem算例實驗數(shù)據(jù)對比 4.1.2 實驗二 表3為改進GWO算法與其他算法在Brandimate測試實例上的結(jié)果對比。HA[1]、GA-RRHC[2]、HGWO[6]、Heuristic[11]、MA[12]、IWOA[13]、GLNSA[14]、HLOA[15]、PSO+TS[16]為對比算法。在對比算法中HLOA和HA算法結(jié)果較好,Heuristic算法運行時間最短,但運行結(jié)果最差;改進GWO算法優(yōu)于HGWO算法,取得了5個測試實例的最佳解,且改進算法具有更短的運行時間,與其他算法相比,改進算法具有一定的競爭性。 表4 對比算法在Brandimate算例上的RPD值對比 4.1.3 實驗三 表5為改進GWO算法與其他算法在Hurink測試實例上的結(jié)果對比。HA[1]、GA-RRHC[2]、GLNSA[14]、IATS[15]為對比算法,其中GLNSA、GA-RRHC和HA算法獲得的最優(yōu)解相當(dāng),都獲得了32個測試實例的最佳解,改進GWO算法獲得了30個測試實例的最優(yōu)解,高于IATS算法所獲得測試實例最優(yōu)解的個數(shù)。 表5 Hurink vdata實例實驗結(jié)果對比 文中以最大完工時間為目標(biāo),應(yīng)用改進GWO求解了柔性作業(yè)車間的調(diào)度問題。首先改進了GWO的編碼方案、種群初始化、灰狼變異以及種群更新機制,其次通過交叉鄰域、插入鄰域以及PR鄰域得到GWO算法全局搜索鄰域,接著提出禁忌搜索鄰域以增強GWO算法局部開發(fā)能力。最后將所提算法在已知的著名算例上進行仿真實驗,并與其他算法進行了對比。實驗結(jié)果驗證了改進GWO算法具有一定的優(yōu)越性。3.3 搜索獵物




3.4 TS搜索

3.5 變異操作
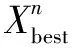
4 實驗
4.1 實驗設(shè)置





5 結(jié)論

