固定效應下部分線性變系數面板模型的協方差矩陣檢驗

李 睿，舒頤超

（上海對外經貿大學統計與信息學院，上海 201620）

0 引言

在傳統的線性面板數據模型中，往往假設誤差項是截面獨立且同方差的，然而很多實際問題與這一假設并不相符，忽略這一客觀事實可能產生錯誤的統計推斷結果。

事實上，針對上述問題，已有許多文獻提出了異方差性與截面相關性的檢驗，并取得了一系列成果。例如，Baltagi等（2007）[1]考慮了面板數據的一般異方差誤差分量模型，并針對兩個誤差分量中的異方差特征提出了同方差的聯合拉格朗日乘數（LM）檢驗；Ledoit 和Wolf（2002）[2]分析了標準協方差矩陣在維度較大，特別是樣本量很大時，是否依然有效；Baltagi 等（2011）[3]提出了一種新的固定效應面板數據回歸模型的擾動球形度檢驗方法；Baltagi 等（2017）[4]分別研究了面對弱因素與強因素兩種情況時，固定效應下球度檢驗的漸近功效；陳冉冉和李高榮（2019）[5]在混合效應面板數據模型中研究了球形檢驗；Hu 等（2021）[6]針對具有固定效應的非參數時變系數面板數據模型提出了球形度和單位矩陣的零值檢驗。然而，這些成果都集中于對參數和非參數模型的討論，而針對半參數面板模型的相關檢驗較少，特別是對帶有固定效應的部分線性時變系數面板模型的研究還暫時未見文獻討論。基于此，本文在此模型上展開討論，具體地：

其中，Zit=(Zit,1,…,Zit,p)?為p維列向量，Xit=(Xit,1,…,Xit,q)?為q維列向量，β=(β1,…,βp)?為未知參數向量，α(t/T)=(α1(t/T),…,αq(t/T))?為q×1維未知函數向量，μi是不可觀察的個體固定效應，誤差項εit對于每個個體i都是平穩的，并且與Zit、Xit和μi都是不相關的。出于模型識別性考慮，假設。

1 模型估計

關于模型（1）已有很多估計方法，如Li 和Ullha（1998）[7]提出了可行的廣義最小二乘（GLS）估計方法；Zhang 等（2011）[8]通過經驗似然來進行參數估計；Ai 等（2014）[9]提出了半參數最小二乘虛擬變量估計器（SLSDVE）參數分量和非參數分量的級數估計量；Hu（2017）[10]通過多元局部線性擬合、變換技術和輪廓似然法，研究了半參數固定效應估計量、半參數隨機效應估計量及其漸近性質；Zhao等（2017）[11]通過取橫截面平均值消除固定效應和局部線性虛擬變量來進行估計；曹連英和畢琳（2020）[12]基于該測量誤差模型進行了嶺估計。本文就是利用Zhao等（2017）[11]的方法研究半參數面板模型的協方差檢驗問題。

具體模型是：

其中，Y=(Y11,…,Y1T,…,YNT)?，Z=(Z11,…,Z1T,…,ZNT)?，ε=(ε11,…,ε1T,…,εNT)?，μ=(μ2,…,μN)?；D=(-1N-1,IN-1)??1T，1T表示全是1的T維列向量，?表示克羅內克積；，其中，ut=t/T,t=1,2,…,T。

利用局部線性方法[13]估計變系數函數α(?)，假設α(?)二階導數連續可微，?ut,ut?(u-h,u+h)，α(?)可以近似地寫為：

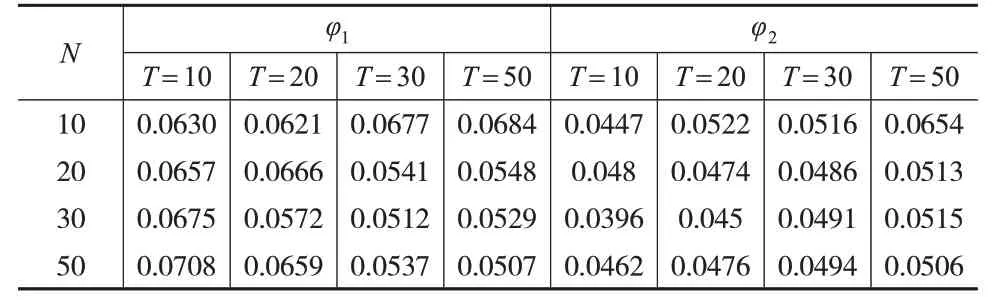
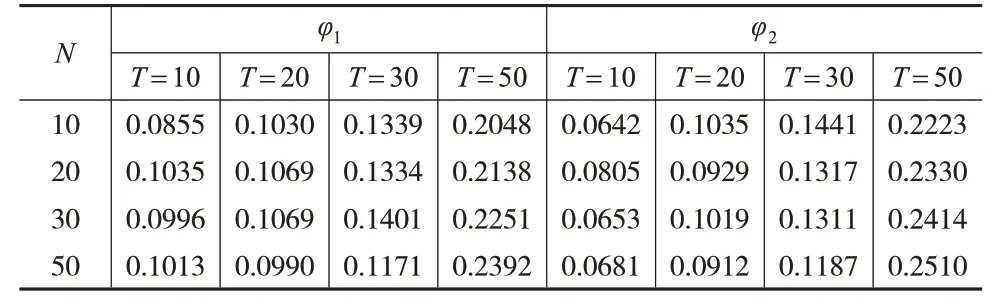
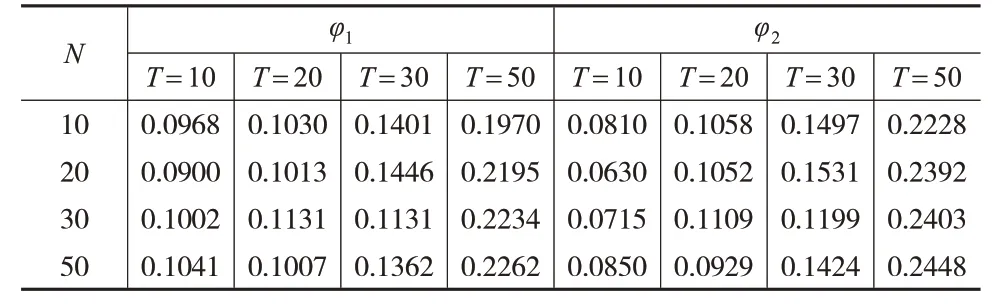
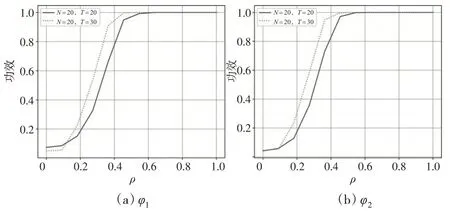
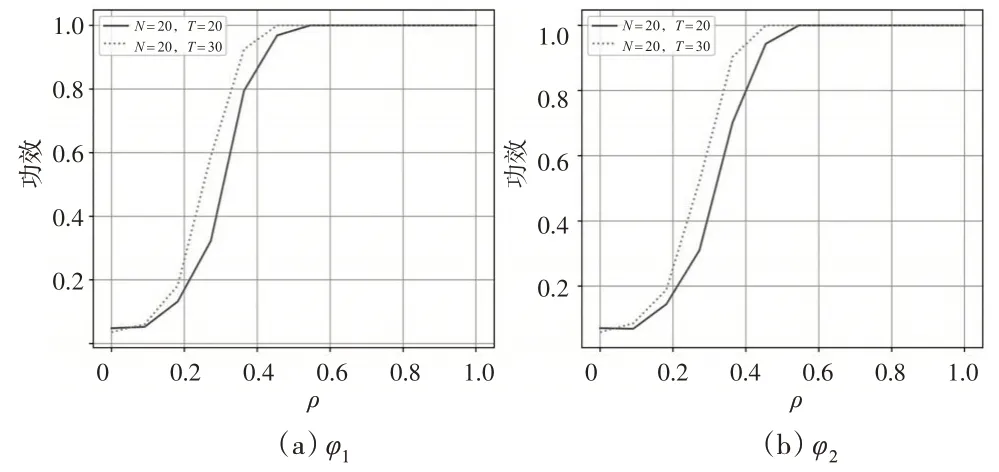
其中，0

具體地，通過輪廓最小二乘估計，可得：

令：

將式（4）代入式（2），可得：

由此可以得到μ的估計：

2 協方差陣的檢驗

模型中隨機擾動的異方差性和截面相關性的識別是統計推斷的關鍵，本文考慮在N、T較大時，如何構造假設檢驗過程，研究部分線性時變系數面板模型的球形檢驗和單位陣檢驗問題。下面介紹一些假設條件：

假設1：假設ε1,ε2,…,εT獨立同分布于N()0,ΣN，其中。

假設2：Xit、Zit和εit相互獨立，并且滿足，其中M和K是正常數。

2.1 球形檢驗

考慮如下球形檢驗問題：

H1意味著協方陣存在異方差性或者截面相關性，或者二者均有。

然而εit是不可觀測的，本文基于前述估計的擬合殘差建立檢驗統計量，簡單計算可得：

注意到，ΣN對應的樣本協方差矩陣為當N固定，T→∞時，可直接使用似然比方法[14]進行檢驗；當N>T時，S是奇異陣，似然比檢驗方法是不可行的。John（1972）[15]提出如下球形檢驗統計量：

其中，S是樣本協方差陣。tr(S)為協方差矩陣S特征值的均值，并且可以證明當N→∞時，在原假設下（詳見下文證明）。因此，原假設H0等價于-IN=0。本文用U=來度量協方差矩陣S和單位矩陣之間的偏差。顯然，U的值越大，ΣN與單位矩陣之間的偏差也越大。

當原假設成立，N固定，T→∞時，John（1972）[15]已經證明。

當N和T同階時，Ledoit和Wolf（2002）[2]研究得到：

即：

基于本文模型的估計，可以得到：

基于此構造檢驗統計量φ0：

進一步考慮到ε?t代替誤差εt時產生的偏差，對φ0進行偏差修正得到φ1：

2.2 檢驗統計量φ1 的漸近性質

為了進一步研究φ1的漸近性質，先介紹如下正則條件：

C1：系數函數α(?)具有二階連續導函數。

C2：核函數K(?)在支撐集[-1,1]上是對稱的。

C3：窗寬滿足h→0 ，Th→∞，Nh→∞，并且nTh8→0。

引理1：如果假設1 和假設2 以及條件C1 至C4 成立，那么當N→∞，T→∞時，有：

證明：引理1 的證明過程與Zhao 等（2017）[11]定理3.4類似，此處忽略。

引理2：在假設1和假設2以及條件C1至C4下，有：

證明：引理2 的證明過程可參考Baltagi 等（2017）[4]的引理1（a）的證明過程，本文不再贅述。

命題1：如果假設1和假設2以及條件C1至C4同時成立，則有：

進一步有：

其中：

結合引理1以及條件C3和條件C4，可以得到：

簡單計算可得：

所以：

綜合式（13）和式（14），命題1證畢。

命題2：如果假設1 和假設2 以及條件C1 至C4 成立，那么可以得到：

證明：結合引理1及條件C3和C4得到：

定理1：在假設1 和假設2 以及條件C1 至C4 下，當N→∞，T→∞時，有φ1依分布收斂于標準正態分布，即：

于是：

類似地，有：

因此：

所以，當N→∞，T→∞時，結合條件C1和C4，有：

2.3 單位陣檢驗

近一步檢驗協方差矩陣是否是單位陣，考慮原假設H0:Σn=In,根據文獻[2]提出如下統計量：

并證明在假設成立且→C時，有：

基于式（2）中的估計，可以構造如下統計量：

2.4 檢驗統計量φ2 的漸近性質

定理2：在假設1 和假設2 以及條件C1 至C4 下，當N→∞，T→∞時，有φ2依分布收斂于標準正態分布，即：

證明：由式（17）可得：

其中：

結合引理2和命題1可得：

由于當原假設H0成立時，σε=1，因此，結合條件C3和C4，有：

基于上述結果，并結合φ2的表達式和式（16），定理2證畢。

3 數值模擬

本文通過經驗分布和統計功效來評估兩種檢驗方法的合理性和穩健性。數據的生成過程如下：

其中：

vit和ξit是獨立同分布于N(0,1)的隨機變量。假設個體固定效應為：

當誤差項εit滿足上述三種情形時，對N=10,20,30,50和T=10,20,30,50 都進行1000次重復模擬。

當誤差項εit滿足情形（1）時，在顯著性水平α=0.05時，表1給出了模型（19）球形檢驗統計量φ1以及單位陣檢驗統計量φ2的經驗顯著性水平。

表1 情形（1）下檢驗統計量φ1、φ2 的經驗顯著性水平

從表1 中可以得到：（1）當N和T都較大時，統計量φ1、φ2的經驗拒絕率均在0.05 左右，并且隨著N和T的增大，經驗顯著性水平逐漸接近0.05。（2）對于較大的N和較小的T,檢驗結果略大于α，這和定理1 以及定理2推導出來的理論結果一致。

當誤差項εit滿足情形（1）和情形（3）且ρ=0.1時，表2和表3給出了模型（19）統計量φ1、φ2在α=0.05 時的經驗顯著性水平。

表2 情形（2）下統計量φ1、φ2 的經驗顯著性水平

表3 情形（3）下統計量φ1、φ2 的經驗顯著性水平

從表2 和表3 中可以得到：（1）當誤差項εit中存在異方差性和截面相關性時,在原假設H0下，經驗顯著性水平明顯大于0.05。（2）隨著N和T的增大，φ1和φ2的經驗顯著性水平越來越大，說明檢驗效果隨著樣本量的增大而變顯著。

當模型（19）中的誤差項εit符合情形（2）和情形（3）時，為了表明檢驗問題的備擇假設H1成立，圖1和圖2給出了N=20,T=20 和N=20,T=30 兩種情況下統計量φ1、φ2的功效隨ρ變化的函數曲線圖。

圖1 情形（2）的檢驗統計量的功效曲線

圖2 情形（3）的檢驗統計量的功效曲線

從圖1、圖2中可以得到以下結論：

（1）若ρ的取值固定，統計量φ1和φ2的功效都會隨著T的增大而增大，則說明當備擇假設H1為真時，樣本量越大，越能正確地拒絕原假設。

（2）若N和T的取值固定，統計量φ1、φ2的功效都會隨著ρ的增大而增大，并且迅速增大到1，則說明樣本量越大，增大到1的速度就越快。

4 結論

協方差檢驗是研究模型異方差性和截面相關性的重要方法之一，本文在帶有固定效應的部分線性時變系數面板模型框架下，對于輪廓最小二乘回歸下的擬合殘差提出了協方差矩陣的球形檢驗和單位陣檢驗方法，并證明了對應的統計量的漸近正態分布和大樣本性質。同時，基于蒙特卡洛模擬的經驗拒絕概率和檢驗功效結果進一步驗證了所提檢驗方法的穩健性和有效性。

本文的協方差矩陣檢驗局限于誤差項符合正態分布的約束，這在一定程度上限制了檢驗方法的普適性，統計量的構造是否受到分布類型的影響以及如何構造等問題都值得進一步思考，具有一定的研究意義。另外，對于高維協方差矩陣的檢驗來說，計算量是巨大的，這對傳統的檢驗方法提出了挑戰。已有學者提出了隨機矩陣投影的方法等，而是否可以在高維背景下建立其他更有效的檢驗方法也值得進一步思考。