基于特征樣本的變參數模型估計方法研究

李 原，王 晶

（1.山西財經大學統計學院，太原 030006；2.太原師范學院經濟與管理學院，山西 晉中 030619）

0 引言

固定參數的時間序列回歸模型只能反映某個時間段內變量平均狀態下的關系，而現實中很多經濟變量間的關系并不是一成不變的，會隨著社會的發展、技術的進步以及經濟結構的轉變等而發生變化，這種動態關系就需要通過變參數模型來體現。傳統的變參數模型主要是狀態空間模型、面板數據模型以及分位數回歸、門限回歸模型等。估計變參數模型的方法一般采用卡爾曼濾波等濾波方法。

國內外不斷有文獻提出變參數估計的新方法和新思路。Rajan 等（1997）[1]較早地提出了一種將馬爾可夫鏈蒙特卡羅方法應用于時變自回歸模型的參數估計方法，該模型的時變系數由基函數建模，然后采用Gibbs方法估計參數。Orbe等（2007）[2]提出了一種非參數方法來估計看似無關的回歸方程模型中的時變系數，該方法允許將交叉和時變限制合并到參數中，估計量是以封閉形式得到的，不需要用迭代方法來計算。Escobar（2012）[3]研究了隨機系統在三種不同的隨機擾動下的連續時變參數估計問題。Andrea 和Lloyd（2018）[4]提出了一種通過將時變參數視為具有未知系數的分段函數來估計周期性時變參數的方法。這種方法使用非線性濾波，允許得到的參數估計在形狀上具有更大的靈活性，同時仍保持周期性。Arnold 和Lloyd（2017）[5]提出了一種利用非線性貝葉斯濾波估計周期性時變參數的方法。該方法將時變參數視為具有未知系數的分段函數，并使用集合卡爾曼濾波器（EnKF）進行估計。

國內也有一些文獻討論了變參數估計的新方法。鄧自立和解三名（1989）[6]、王建國（1990）[7]主要討論了自回歸模型的時變參數估計，采用了自適應濾波方法。鄧衛強等（2011）[8]對譜估計方法進行了改進，用遺傳算法進行了時變參數估計。陳云仙等（2017）[9]也討論了時變參數的貝葉斯估計。

上述文獻從不同角度對時變參數的估計方法進行了研究，每個角度都有其特點。本文擬從一個全新的角度，提出一種特征樣本機器采樣推斷方法來估計時變參數。

1 特征樣本概念及采樣

特征樣本是在某變量特定的值域范圍內按照變量的分布特征采用機器采樣的方法生成的隨機樣本[10]。每個特征樣本都有目標變量和標識變量兩個要素，表示為（x,y），或者將x作為標識變量獲得目標變量y，或者將y作為標識變量獲得目標變量x，每個特征樣本都有特定的樣本容量，也有標識變量和目標變量的值域。特征樣本的一般形式可以表達為：

其中，ζ表示目標變量的特征樣本，n是樣本大小，x與y的關系及分布特征用函數式y=f(x)表達，ψ[a,b]是目標變量的值域。

特征樣本的采樣要先確定變量的分布特征，本文的分布特征不是指典型的概率分布，而是更廣泛的變量特征。在確定分布特征的基礎上，再確定目標變量或標識變量的值域，同時確定所需要的樣本容量，就可以利用特定的計算機程序來采樣。

特征樣本的采樣思想可以歸納為以下幾點：第一，特征樣本不是實際觀察樣本，而是依據經驗獲得分布特征后按照特定方法產生的隨機樣本；第二，特征樣本是在特定取值區間的樣本；第三，特征樣本是可以重復采樣的樣本；第四，特征樣本的分布特征，既可以通過已有經驗確定，也可以通過觀察現實數據得到；第五，特征樣本采樣總體上屬于單樣本的蒙特卡羅采樣范疇。

特征樣本可以分為分布型樣本和曲線型樣本，需要使用不同的方法進行采樣。已有研究設計了特征樣本采樣的10種方法，包括適用于分布型樣本的標準分布法、比例分布法、反函數分布法、分區頻率分布法、分區值域分布法和適用于曲線型樣本的標準曲線法、反函數曲線法、非標準曲線法、比例曲線法、自助曲線法。這些方法可以實現常見的13種類型的特征樣本采樣。

按照這些采樣方法，可以在計算機程序輔助下，分別對正態分布樣本、均勻分布樣本、偏態分布樣本、線性增長樣本、線性遞減樣本、正態曲線樣本、反正態曲線樣本、偏態曲線樣本、指數增長曲線樣本、指數遞減曲線樣本、S增長曲線樣本、反S 曲線樣本、模擬曲線樣本等常見特征變量采樣。

2 基于特征樣本采樣的變參數模型估計方法

除了有固定系數的特征樣本模型估計方法，高艷平和王晶（2019）[11]還從數學及模擬仿真的角度證明了特征樣本重復抽樣回歸（FSR）方法的優越性。基于此，本文將基于特征樣本設計一套變參數模型估計方法，實現小樣本情況下的變參數模型估計。

2.1 特征樣本變參數模型估計的思想

特征樣本重復抽樣回歸方法根據對變量特征的把握來設定變量的分布形態和參數，然后按分布特征重復采樣生成一系列特征樣本。對每一個特征樣本進行回歸都可以得到一組參數估計結果，分別對全部m個特征樣本回歸就可以得到一系列的系數估計結果，并據此模擬每個系數自身的分布特征，判斷回歸系數的取值和置信區間。FSR 方法重復抽樣得到的一系列特征樣本也為變參數模型的估計提供了一種新的思路——對特征樣本進行重新組合，分別估計每一期的系數，可以直接得到模型的變參數結果。具體來講，FSR方法在時間序列的重復抽樣過程中形成了一系列特征樣本，那么如果將每個樣本的第1期匯總在一起，就得到了解釋變量和被解釋變量第1期的分布，則可以據此進行第1 期系數的估計；后面每一期都同理，可以通過n次估計得到第1 至第n期的系數估計結果。進一步，根據每一期系數的估計結果，還可以對系數的變動趨勢進行自回歸估計，探究變量之間關系的變動趨勢。這種方法稱為特征樣本變參數回歸（Features Sample Variable Parameter Regression，FSVR）方法。

FSVR 方法是建立在特征樣本m次重復抽樣的數據基礎上的，但是其數據組合形式與回歸方式有所不同。FSR 方法進行特征樣本重復抽樣的特點是樣本容量n極小化（大于k+1即可，k是解釋變量個數），重復抽樣次數m極大化（比如一千次、一萬次）。一次特征樣本采樣就形成了一個包含被解釋變量與k個解釋變量在內的樣本容量為n的多變量復合特征樣本，FSR方法的重復采樣最終形成了m個樣本量為n的復合特征樣本。

FSVR方法的建模思想就是將FSR方法重復采樣得到的特征樣本進行重新組合，將每一期的m次抽樣結果組合為該期的樣本，就可以得到n個樣本容量為m的分期樣本。通過對這些特征樣本的多期回歸，不僅能夠得到模型的變系數結果，而且可以根據估計結果來尋找各期系數的變動規律，得到在形式上與狀態空間模型類似的結果。構建的主方程類似狀態空間模型中的“信號方程”或者“量測方程”。用系數構建的自回歸模型，類似狀態空間模型中的“狀態方程”。

2.2 特征樣本變參數模型的估計方法和步驟

2.2.1 按照分布形態和變量值域進行采樣

特征樣本變參數模型是建立在FSR 方法的基礎之上的，所以變參數模型的構架和估計首先需要根據變量特征和值域進行特征樣本的重復采樣，這一步與FSR 方法相同。對于樣本容量為n的時間序列模型，重復采樣后獲得的樣本是一個（k+1）*n行、m列的矩陣。

2.2.2 對特征樣本進行重新組合，獲得每一期的子樣本

如果要估計變參數回歸模型，就要對初始特征樣本進行重新組合，獲得每一期的子樣本。具體的做法是：先將上述FSR特征樣本矩陣進行轉置，轉置后全部數據的矩陣見式（2）。

然后從該樣本中分別提取第t期的數據，組合成一個新的m行、k+1 列的矩陣，即為第t期的子樣本。其中y為被解釋變量，x為解釋變量，解釋變量個數為k，每個變量樣本容量為n，抽樣次數為m。每期的特征樣本矩陣見式（3），一共可以得到n個樣本容量為m的子樣本。

2.2.3 分期回歸，獲得每一期的估計系數

根據重復抽樣和組合獲取的子樣本，可以對每一個子樣本進行單方程參數估計，獲得每一期的系數估計結果，類似狀態空間的“信號方程”。“信號方程”的模型形式可以選擇線性回歸、非線性回歸等形式，但是全部n期的“信號方程”形式必須一致。以最常見的多元線性回歸為例，“信號方程”的形式為：

選定模型形式之后，用最小二乘法或極大似然法來估計每一期子樣本的回歸系數，其中為第t期回歸模型的常數項，為第t期回歸模型中第i個變量的估計系數，i=1,2,3,…,k。

需要注意的是，在FSR 方法的應用中，很多變量是遞增或者遞減的分布形態，所以，在m次抽樣中，其初期和末期的變量取值實際上都是固定的最大值或者最小值，是無法進行系數估計的常數。考慮到變參數模型的普遍適用性，只進行第2 期到第n-1 期的分期系數估計，第1 期和第n期系數用下文給出的方法推算。

2.2.4 估計系數的波動規律并據此推算期初和期末的系數

在獲得第2至第n-1期變系數的基礎上，對單個系數序列進行自回歸，可以估計其變化規律，類似狀態空間模型中的“狀態方程”。

設各期系數之間的關系為：

可以根據每個參數的估計結果進行自回歸估計，這樣就得到了各期系數的滯后一期的變化規律。根據式（5）的估計結果，可以進行期初和期末系數的推算，即：

如圖1所示，路由開銷隨著節點停留時間的延長而降低，這是因為網絡拓撲結構的變化不再頻繁所致。圖2表明網絡整體的端到端時延隨節點停留時間的增加而降低。圖3表明分組投遞率隨節點停留時間的增加而提高。如圖4所示，路由發現頻率隨節點停留時間的增加而降低。

2.2.5 特征樣本變參數模型的最終表達式

經過以上步驟就得到了變量之間每一期的回歸系數，以及系數隨時間波動的自回歸方程，實現了時間序列數據的變參數估計。變參數模型的最終表達式為：

2.2.6 估計特征樣本整體模型

為了反映模型的整體擬合情況，對模型系數進行分期估計以后，還可以對模型進行不分期的整體估計。模型整體估計的結果是固定系數，實際上是分期系數的均值。

對模型中每個變量每次采樣的特征樣本求均值，就得到了一個包含每個變量n期均值、樣本容量為采樣次數m的新樣本，根據該樣本進行最小二乘估計，可以得到每個變量均值的估計系數，即固定系數。

2.2.7 參數估計結果的檢驗

（1）模型整體擬合優度檢驗

特征樣本變參數模型擬合優度檢驗的思路與普通最小二乘估計一致，都是考察殘差平方和在被解釋變量離差平方和中的比重，這個比重越小，說明模型的擬合優度越好。把變參數回歸中n個回歸方程作為一個整體時，可以得到整體殘差平方和（TSSE）與被解釋變量的整體離差平方和（TSST）。特征樣本變參數模型的擬合優度R2用整體被解釋變量離差平方和中除去整體殘差平方和的部分所占的比重來表示，R2越大，表示變系數模型的整體擬合優度越好。

（2）模型整體固定系數顯著性水平檢驗

對于按變量均值估計的固定系數，采用t檢驗方法，可獲得對模型固定系數估計的可信度評價。

（3）各期可變系數顯著性水平檢驗

一個包含k個自變量的變參數線性回歸模型每期有k+1個系數。對每個系數進行一次t檢驗，可以獲得t值和對應的P 值，據此可以對系數估計結果進行判斷和評價。t 檢驗系數的標準誤采用每期估計的殘差和對應的方差-協方差矩陣來估計。

3 應用案例

根據經濟分析的需要，建立一個有關居民消費價格指數（cpi）的時變參數模型，解釋變量為人均消費支出（income）與貨幣供應量（m），建立如下變參數模型：

其中，αt和βt分別是各期截距項和變量項可變系數。分析時期是從2011 年到2020 年的10 年。在分析中根據經驗可以知道該時期的變量特征，故采用特征樣本參數估計方法。各個變量的分布特征如表1所示。

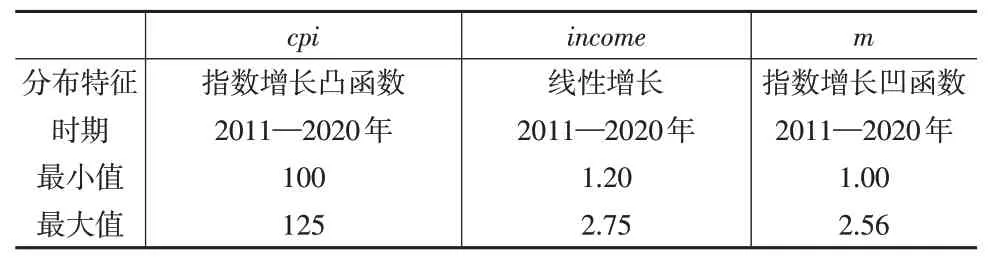
表1 變量分布特征

依據變量分布特征對每個變量進行特征樣本采樣，在采樣程序中輸入解釋變量數k=2，樣本期n=10，采樣次數m=500，得到500 個樣本。按前述步驟和程序進行運算，設定cpi的凸函數參數為0.8，m的凹函數參數為1.2，參數估計和檢驗后得到結果如表2所示。

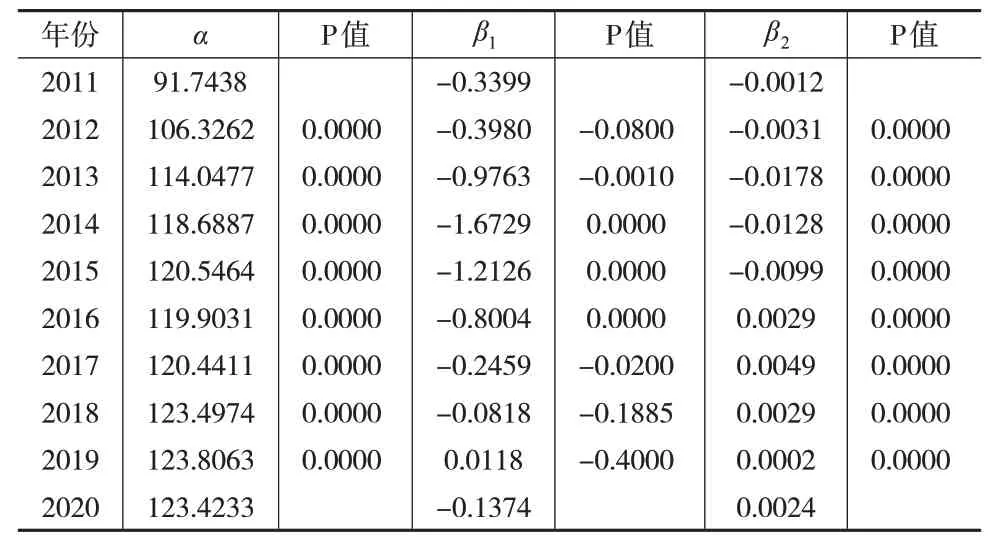
表2 居民消費價格模型可變系數估計及t檢驗結果

各可變系數的自回歸方程為：

整體均值固定系數的方程及其檢驗結果為：

模型的分期系數和固定系數的t 檢驗結果均顯著，擬合優度R2為0.7494，擬合效果較好，模型整體估計結果有效。

根據式（10）的估計結果，人均消費支出對居民消費價格指數的負面影響是逐漸縮小的，而貨幣供應量對居民消費價格指數的影響由負向轉為正向，并且正向影響隨時間推移而增強。與固定參數模型相比，這一估計結果不僅體現了人均消費支出和貨幣供應量對居民消費價格指數的影響，而且更加精確地反映了這種影響隨時間變動的情況。

4 結論

本文提出了一種基于特征樣本的變參數模型估計（FSVR）方法，通過對重復抽樣的每一期樣本分別回歸來實現時間序列模型的變參數估計。得出以下結論：（1）FSVR方法是一種新的方法，該方法簡便易行，給出了變參數模型參數估計的另外一種思路。在社會科學研究中，很多時候存在數據短缺問題，有了特征樣本采樣方法，就可以根據經驗來獲取樣本，依據特定的程序，把可變系數估計出來。（2）FSVR 方法符合貝葉斯統計原理，在進行參數估計之前，依據經驗給出參數的先驗分布，然后將基于先驗信息的特征樣本納入參數估計過程，這樣就能夠把握大方向和減少偏誤。（3）利用FSVR 方法估計模型的可變參數，是基于某種分布通過計算機重復采樣對參數進行模擬，符合蒙特卡羅模擬原理。（4）FSVR 方法將按時期長度得到的樣本容量轉換成按采樣次數計算的樣本容量，可以將小樣本估計變成大樣本估計。（5）FSVR方法估計的可變參數需要進行兩個層次的檢驗。在分期層次上，設計了系數的t檢驗；在整體層次上，設計了整體固定系數檢驗和擬合優度檢驗，模擬擬合效果和參數估計效果優劣都可以通過這些檢驗來完成。

本文應用實例的估計結果顯示，該方法可以得到較好的變參數估計結果，FSVR 方法適用于社會科學領域小樣本變參數估計。當然，本文僅對FSVR 方法的原理、檢驗和應用進行了介紹，后續還需要對估計殘差的檢驗、與狀態空間模型對比的優劣及估計結果的穩健性等方面進行進一步的研究。