哈密頓量宇稱-時間對稱性的刻畫*

張慧潔 賀衎

(太原理工大學數學學院,太原 030024)

宇稱-時間(PT)對稱性理論描述了具有實能級的非厄密特哈密頓量,在量子物理學和量子信息科學中起著重要作用,是量子力學中活躍且重要的主題.研究者們對如何描述哈密頓量的PT 對稱性的問題給予了高度關注.本文基于PT 對稱理論和哈密頓量歸一化特征函數,提出了算子F 的定義.然后,在找到算子CPT和算子F 的對易子和反對易子的特性后,給出了刻畫了無量綱情況下哈密頓量的PT 對稱性的第一種方法.進一步研究發現,該方法還可以量化哈密頓量在無量綱情況下的PT 對稱性.此外,提出了另一種基于哈密頓量特征值實部和虛部來描述哈密頓量PT 對稱性的方法,該方法僅用于判斷哈密頓量是否具有PT 對稱性.

1 引言

量子力學中的一個重要理論是宇稱-時間(PT)對稱理論.PT 對稱理論的研究始于量子力學模型的研究.量子力學是數學希爾伯特空間中的態與實驗中可測概率間的聯系.由于概率是實的且是正的,所以要求概率所對應的希爾伯特空間上的向量的范數必須是正的.由于概率是守恒的,是不隨時間變化的,即時間酉演化,所以希爾伯特空間上的任意兩個不同向量之間的內積在時間上必須是常數.所以有了量子力學中任何量子理論都不能違背的兩個基本公理: 1)能級是實的;2)時間酉演化.想要滿足量子力學的兩個基本公理需要限制數學上的哈密頓量是實的、對稱的,但這不是一般的條件.事實上,物理情形中存在復哈密頓量,許多研究者將哈密頓量H從實空間推廣到了復空間[1],這就有了更一般的條件要求: 哈密頓量是厄密的.

1998年,Bender 和Boettcher[2]發現具有實譜的非厄密哈密頓量具有PT 對稱性.后來Bender[3]指出,因為函數PT 對稱,所以考慮哈密頓量H=+是PT 對稱的.通過考慮哈密頓量H=+的δ 展開H=,發現加入微小攝動的哈密頓量的能級在δ≥0時,哈密頓量的能級仍然是實的[4],所以引入了PT對稱理論來描述有實能級的非厄密的復哈密頓量.擁有實能級的復哈密頓量可以是PT 對稱的哈密頓量,也可以是厄密的哈密頓量,但是不能同時都是.但是實哈密頓量可以既是PT 對稱的哈密頓量,又是厄密的哈密頓量.實際上,早已有文獻說明非厄密PT 對稱哈密頓量已經被用來描述小球量子系統的基態、場理論和Lee-Yang 邊緣奇點等現象[5–7].文獻[2]描述了PT 對稱理論中新的復哈密頓量不同于經典的和量子的性質,刻畫了非厄密哈密頓量的能級譜.文獻[8]說明PT 對稱的哈密頓量的能級譜仍然滿足量子力學的兩個公理,可以把PT 對稱量子力學視為普通量子力學的復雜版本.

關于PT 對稱理論及其應用的研究也不斷深入[9?11].文獻[9]研究了PT 對稱耦合振子中的二重躍遷.文獻[10]討論了PT 對稱哈密頓量在量子信息科學中的應用.利用PT 對稱哈密頓量的不等價實驗解決了使用PT 對稱哈密頓量執行指數級快速數據庫搜索(量子計算機不可能完成)與超光速信息傳遞的不可能性以及局域操作下糾纏的不變性等基本信息原理之間的沖突.充分評估了使用PT 對稱哈密頓量提出的更快的時間演化和狀態識別的方案.文獻[11]利用PT 對稱理論的非線性性質,說明在PT 對稱性下,增益和損耗可以為波導系統提供最佳的和靈活的控制.這使得PT 對稱性可能有很多物理上的應用,如光開關、單向無反射PT-光學頻率下的對稱超材料、單模PT 對稱微環激光器、CPA 激光器和聲子激光器等.

對于哈密頓量的PT 對稱性的刻畫同樣值得進一步的研究.2018年,El-Ganainy 等[12]關注了非厄密物理學和PT 對稱性間得與失的相互作用導致的新特征.2020年,Pi 等[13]說明了復Berry相拓撲結構和PT 對稱破缺之間的關系.同年,俞上等[14]提出了一種基于擴張哈密頓量的弱測量來表征哈密頓量的PT 對稱性的理論和實驗方法,該方法也可以用來判斷哈密頓量H是否PT 對稱.

本文給出了哈密頓量PT 對稱性理論上的其他刻畫方式,主要結構如下: 第1 節介紹本文用到的一些基礎知識;第2 節基于PT 對稱理論,定義與哈密頓量歸一化特征函數相關的算子F,刻畫并量化哈密頓量的PT 對稱性;第3 節通過使用哈密頓量能級的實部和虛部,利用已定義算子F,給出判斷哈密頓量PT 對稱性的另一種方法;第4 節總結本文的研究內容.

2 基本理論

1) 對易子和反對易子[15]

對易子:[A,B]=AB-BA.

反對易子:{A,B}=AB+BA.

對易子與反對易子通常與一對算子的可交換性和不可交換性相關,也與算子的對稱性與不可對稱性有關,可以作為研究量子力學問題時的工具.

2) 給定無量綱哈密頓量的參數范圍下的能級情況[2,16]

哈密頓量H的形式:

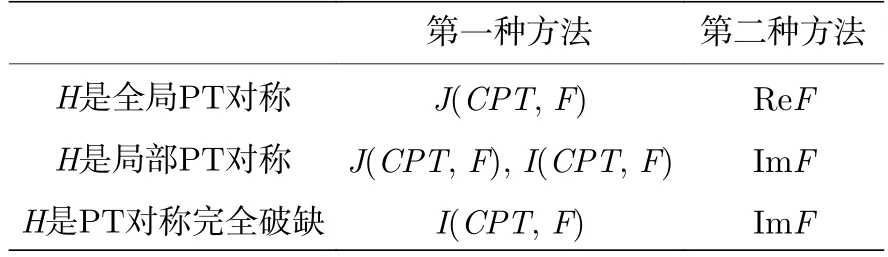
其中N是實數(N>0),m不等于0,和分別是動量運算符和位置運算符(在本文中,可以將,視為無量綱).有哈密頓量H的一般譜: 哈密頓量H的能級是參數N的函數.值得注意的是: 當N≥2時,能級譜是正的也是實的;N=2 對應于諧振子,其能級為En=2n+1;當1

3) 量子力學的兩個公理: 能級是實的;時間酉演化.

4) PT 對稱理論[3]

PT 對稱理論核心的想法是用哈密頓量具有時空反演對稱性(PT 對稱性)這個較弱的條件代替量子理論中厄密的哈密頓量.用PT 對稱性代替厄密性條件時,如果哈密頓量的對稱性沒有被打破,哈密頓量將表現出厄密哈密頓量描述的所有量子特征.而且PT 對稱的哈密頓量有和PT 算子可交換的性質,即有[H,PT]=0 .PT 對稱的哈密頓量在時間反演算子T對時間的反演(p →-p,x →-x,i→-i)和宇稱算子P對于空間的反轉(p →-p,x →-x)的共同作用下是不變的.但是哈密頓量H既不在宇稱算子P下不變,也不在時間反演算子T下不變.因此對于PT 對稱的哈密頓量H,有H=HPT=PTH.

5) 狄拉克δ 函數[17]

為了表示物理學中的質點、點電荷、瞬時力等不連續分布于空間或時間中,而是集中在空間的某一點或時間的某一瞬時的抽象模型的密度分布引入的概念.數學表示為δ(x)=0,(x0),=1.該表達式規定函數在0 點取非零值,其他點取0 值.不規定δ 函數在0 點的大小,函數值的大小由第二個積分式決定.

6) 本文所用名詞解釋

完全PT 對稱的哈密頓量: PT 對稱不破缺的哈密頓量,特征值全部為實特征值,整體隨時間做酉演化.

局部PT 對稱的哈密頓量: PT 對稱破缺的哈密頓量,特征值為實特征值和復特征值對,整體隨時間做非酉演化,局部隨時間做酉演化.

PT 非對稱的哈密頓量: PT 對稱完全破缺的哈密頓量,沒有實特征值,只有復特征值對.

哈密頓量的局部PT 對稱部分: PT 對稱破缺的哈密頓量保持PT 對稱的部分,具有實特征值,這些實特征值是哈密頓量特征值的一部分.哈密頓量的PT 對稱部分隨時間做酉演化.

哈密頓量的PT 對稱破缺部分: PT 對稱破缺的哈密頓量不保持PT 對稱的部分,具有復特征值對,這些復特征值對是哈密頓量特征值的一部分.不保持PT 對稱的部分隨時間做非酉演化.

3 利用對易子和反對易子刻畫哈密頓量的PT 對稱性

本節利用對易子和反對易子,進一步研究無量綱的哈密頓量的PT 對稱性.雖然可對角化和非可對角化哈密爾頓量都可以定義具有正CPT范數的希爾伯特空間,但是只有可對角化哈密頓量的特征函數是其退化根子空間的基函數,而非可對角化哈密頓量對應于退化根子空間的基函數不是哈密頓量的本征函數[16].哈密頓量非可對角化的情況比較復雜,所以為了便于研究,需要確保哈密頓量是可對角化的.又由于正則斯圖姆-劉維爾問題的證明結果,特征行列式中不存在多個零點[18]時,哈密頓量H的特征函數在希爾伯特空間中是完備的.因此,本節的研究基于系統的理想假設: 系統中不存在零CTP范數,即特征行列式中不存在多個零點.所以本節研究的哈密頓量是可對角化的,且其特征函數在希爾伯特空間中是完備的.

3.1 重構宇稱算子P,哈密頓量H 的空間表示

設ψn是與哈密頓量H的特征值En相對應的特征函數,?n是哈密頓量H的歸一化特征函數.這意味著:

為了更清晰地表征,可以根據本征函數重構宇稱算子P、哈密頓量H的空間表示,分別表示如下[3]:

宇稱算子P是酉的:P2=1.且有H?n(x)=En?n(x),En是哈密頓量H的能級.

特別地,H?n可以被表示為:H?n=En?n=An?n+Bni?n(An+Bni=En),?n是能級En所對應的本征函數.An和Bn是實數,表示能級En的實部和虛部.

厄密量子力學中,希爾伯特空間內積是具體的[3].對于非厄密的哈密頓量,對PT 空間上的兩個函數f(x)和g(x) 的內積的合理猜測是

這里,PTf(x)=[f(-x)]?,有f(x)的PT范數為

所以哈密頓量H的本征函數?m(x)和?n(x)有新的內積形式.然而,本征函數的PT范數不是正定的:(?m,?n)=(-1)nδmn,當m=n.這是因為在PT 對稱量子力學中,量子態的矢量空間是由能量本征函數構造的,其中一半有范數 +1,另一半有范數-1[3].

3.2 引入線性算子C

在連續對稱理論中,哈密頓量H的對稱性與正負能級的數量有關.這不利于描述哈密頓量H的局部PT 對稱和破缺部分.為了便于描述哈密頓量H的局部PT 對稱和破缺部分,引入了線性算子C.其性質類似于量子場論中的電荷共軛算符.還可以根據本征函數重構線性算子C,其空間表示如下:

線性算 子C是酉的:C2=1,且特征值是±1,C表示本征函數?n(x)的PT范數的符號的測量.因為C是線性算子,所以有C?n(x)=(-1)n?n(x) .線性算子C具有一般的算子表示形式[3]:

則有

其中,An+Bni=En;An和Bn是實數,分別是能量級En的實部和虛部[3].

令K 是一個基于哈密頓量H的本征函數的空間,可以在空間 K 上得到函數f的CPT范數[3,19],如下所示:

其中CPTf(x)=.此內積滿足正范數的要求和量子力學中的酉理論.

3.3 定義與哈密頓量歸一化特征函數有關的算子F

算子G是將復空間中哈密頓量H的特征函數?n與其對應能級En的乘積作為列向量的算子.可以表示為

由CPT算子和哈密頓量H的空間重構,如果?n屬于局部PT 對稱部分,則CPT?n(x)=[?n(-x)]?=?n(x),且能級En是實的,所以CPTH?n(x)=[?n(-x)]?=En?n(x),否則,CPTH?n(x)=[?n(-x)]?[3].

若?n(n=1,2,···,n,···) 屬于哈密頓量局部PT 對稱部分,當m=n時,有(?n(x),?m(x))=若存在?n(n=1,2,···,n,···) 不屬于哈密頓量局部PT 對稱部分,則有上式中的不等號.

令cn=En/∥G∥,an=An/∥G∥,及bn=Bn/∥G∥,則算子G歸一化得到算子F:

由CPT算子和哈密頓量H的空間重構,得到

所以,算子F的CPT 范數為

3.4 刻畫哈密頓量的PT 對稱性

將PTF分為兩部分:PTF=[PT,F]+{PT,F}.其中[3],

對易算子[PT,F]表示PT和F是不可交換,反對易算子{PT,F}表示PT和F是可交換的.

又因為CPT算子是酉的,所以

接下來,將得到∥{CPT,F}∥CPT和∥[CPT,F]∥CPT的界.

因為CPT算子是酉的,CPT2=I,所以

因為?n不總是屬于局部PT 對稱的部分,函數f不一定是完全PT 對稱的,所以f和CPTf不能保證是時間酉演化的.由于CPT算子是酉的,CPT-1算子也是酉的,所以

其中,∥?∥a是算子范數.

這表明,0 ≤∥[CPT,F]∥CPT≤1/2 .

這意味著:

根據I(CPT,F),J(CPT,F) 的范圍和與交換性的聯系的特性,則有:

I(CPT,F)=∥[CPT,F]∥CPT可以表示PT 對稱破缺部分;

J(CPT,F)=∥{CPT,F}∥CPT可以表示PT對稱部分.

若I(CPT,F)=∥[CPT,F]∥CPT=0,表示所有?n屬于PT 對稱部分,即哈密頓量H是全局PT對稱的.

若I(CPT,F)=∥[CPT,F]∥CPT0,表明?n屬于PT 對稱破缺部分,即哈密頓量H是PT 對稱破缺的.

可以得到如下結論:

1)當N<1,哈密頓量H的能級譜中沒有實特征值,不滿足量子力學的兩個公理.此時哈密頓量H是PT 對稱完全破缺的,可以用I(CPT,F)=∥[CPT,F]∥CPT表示.

2)當1

3)對于N≥2,哈密頓量H的能級譜的特征值都是正的實特征值,哈密頓量H是全局PT 對稱的,可以用J(CPT,F)=∥{CPT,F}∥CPT表示.

這意味著I(CPT,F)和J(CPT,F) 是守恒的,且當F為全局PT 對稱的取最后一個等號,這與哈密頓量H的破缺部分和PT 對稱部分是守恒的相一致.

基于上述討論,建立了描述哈密頓量H的PT 對稱性的一種方式.該方法下,哈密頓量H的局部PT 對稱性與哈密頓量H與CPT算子的可交換性有關,哈密頓量H的破缺部分與哈密頓量H與CPT算子的不可交換性有關.該方法可以量化哈密頓量H的局部PT 對稱部分和破缺部分,而不是僅僅判斷哈密頓量H是否是全局PT 對稱的.對于給定的哈密頓量H,可以得到特征值En和相應的特征函數?n,以及算子F的定義,進而得到哈密頓量H的PT 對稱部分和破缺部分.

4 利用哈密頓量特征值的實部和虛部判斷哈密頓量的PT 對稱性

對于僅僅需要區分哈密頓量H是否是全局PT對稱的情況,本節給出另一種較為簡捷的刻畫方式.該方法同樣基于上述定義中的算子F,通過利用哈密頓量H的實部和虛部,刻畫哈密頓量H的PT 對稱性.

4.1 利用CPT 算子和F 算子表示哈密頓量的實部和虛部

本節定義另外一組特殊的算子,使其CPT范數為上一節算子F的實部ReF和虛部ImF的倍數.由算子F和哈密頓量H歸一化特征函數的密切關系可以反映出哈密頓量H的實部或者虛部的情況.

另一方面,

所以,

表明算子F的實部和虛部的和是守恒的.這與確定的哈密頓量H的實部和虛部是守恒的相一致.

4.2 判斷哈密頓量的PT 對稱性

若ImF=0,所有本征函數?n的能級En僅有實部,是實數.此時全部本征函數?n屬于PT 對稱部分,表明哈密頓量H是全局PT 對稱的,反之亦然.若ImF0,表明存在本征函數?n的能級En是具有虛部的,是復數.表明此時的哈密頓量H是PT 對稱破缺的,反之亦然.若ReF=0,所有?n的能級En只有虛部,?n必定屬于PT 對稱完全破缺的部分,表明哈密頓量H是PT 非對稱的,反之不然,是充分不必要條件.

5 結論

本文給出了刻畫哈密頓量H的PT 對稱性的兩種方式: 1)J(CPT,F),I(CPT,F) ;2)ReF,ImF.由于實數和虛數在實驗上是可探測的,后者比前者可能更容易操作.若僅關注哈密頓量H是否是PT 對稱破缺的,而不關注破缺部分的量化,使用ImF的刻畫方式更簡捷.但前者在理論上可能更好,因為使用J(CPT,F) 可以量化哈密頓量的局部PT 對稱部分,而ReF不能用于量化哈密頓量的局部PT 對稱部分.

若哈密頓量H是全局PT 對稱的,只需要關注實部ReF和PT 對稱部分J(CPT,F) .若哈密頓量H是PT 對稱破缺的,而第二種刻畫方式只需要關注ImF,對于第一種刻畫方式需要關注局域PT 對稱部分J(CPT,F) 和PT 對稱破 缺部分I(CPT,F).若哈密頓量H是完全破缺的,可以僅關注ImF和PT 對稱破缺部分I(CPT,F),如表1所列.

表1 比較刻畫哈密頓量H PT 對稱性的兩種方法Table 1.Compare two depiction methods of PT-symmetry of Hamiltonian H.

需要注意的是,當想要判斷哈密頓量H是否是完全PT 對稱破缺時,需要關注I(CPT,F) 是否為0,而不是ReF是否為0,因為ReF不利于區分局部PT 對稱性和PT 對稱完全破缺性.若哈密頓量H是PT 非對稱的,則存在哈密頓量H的本征函數?n的能級En是復數,但不一定是純虛數,所以ReF不一定為0.由于參數N與哈密頓量H能級譜的關聯,此區別主要體現于參數N≤1 的情形.