識別高階網絡傳播中最有影響力的節點*

李江 劉影2) 王偉 周濤

1) (西南石油大學計算機科學學院,成都 610500)

2) (弗里堡大學物理系,弗里堡 1700)

3) (重慶醫科大學公共衛生學院,重慶 400016)

4) (電子科技大學大數據研究中心,成都 611731)

識別網絡傳播中最有影響力的節點是控制傳播速度和范圍的重要步驟,有助于加速有益信息擴散,抑制流行病、謠言和虛假信息的傳播等.已有研究主要基于描述點對交互的低階復雜網絡.然而,現實中個體間的交互不僅發生在點對之間,也發生在3 個及以上節點形成的群體中.群體交互可利用高階網絡來刻畫,如單純復形與超圖.本文研究單純復形上最有影響力的傳播者識別方法.首先,提出單純復形上易感-感染-恢復(SIR)微觀馬爾可夫鏈方程組,定量刻畫單純復形上的疾病傳播動力學.接下來利用微觀馬爾可夫鏈方程組計算傳播動力學中節點被感染的概率.基于網絡結構與傳播過程,定義節點的傳播中心性,用于排序節點傳播影響力.在兩類合成單純復形與4 個真實單純復形上的仿真結果表明,相比于現有高階網絡中心性和復雜網絡中最優的中心性指標,本文提出的傳播中心性能更準確地識別高階網絡中最有影響力的傳播者.

1 引言

現實世界中,許多具有擴散效應但僅由局部相互作用驅動的動力學過程可以用復雜網絡上的傳播來描述,如社交網絡上的流行病與謠言傳播[1,2]、電力網絡上電站的級聯失效[3]、交通網絡上的道路阻塞[4]、計算機網絡上的病毒傳播[5]等.失控的傳播可能對社會經濟及人們生活造成大范圍的負面影響,如COVID-19 大流行影響經濟發展[6],謠言傳播引起民眾恐慌[7],電力網絡中部分設備故障導致電網癱瘓[8].由于網絡結構的異質性,網絡中節點的傳播影響力具有顯著的差異[9].如在Twitter與Facebook 平臺僅有少量賬戶的信息被廣泛分享[10],COVID-19 中10%最具傳染性的宿主導致近80%的感染[11].網絡傳播中影響力最大的節點被稱為最有影響力的傳播者.識別最有影響力的傳播者是快速、有效地控制傳播過程的關鍵步驟.節點中心性利用網絡拓撲結構度量節點在網絡中的重要性.如基于鄰居數目的度中心性[12]、H-index 中心性[13]、k 殼中心性[14]、集體影響中心性[15]等,基于路徑的接近中心性[16]、介數中心性[17]、子圖中心性[18]以及基于特定動力學過程迭代穩態的指標,如特征向量中心性[19]、PageRank[20]、非回溯中心性[21]等.隨后,大量基于中心性的方法被提出,識別網絡中最有影響力的傳播者的算法性能不斷提升,并從單層網絡推廣到多層網絡[22–28].

已有識別最有影響力傳播者的研究主要針對描述節點間成對關系的簡單網絡.簡單網絡用節點表示個體,邊表示兩個節點間的交互.然而現實中許多系統存在超越點對的成組交互,例如學術論文通常由團隊共同完成[29],謠言與思想的傳播在小范圍群體中被加強[30].由3 個及以上個體組成的群體交互被定義為高階交互,單純復形和超圖是兩種描述高階交互的數學工具[31].單純復形是由一系列單純形組成的集合.一個k階單純形由k+1個節點組成,且這些節點的任意節點子集也構成單純形.如在科學家合作網中,若4 個作者組成一個3 階單純形,自然其中任意2 個作者,任意3 個作者也具有合作關系.在超圖中,一條超邊可包含任意數量的節點,表示這些節點相互影響.相比于單純復形,超圖不要求高階交互的所有子交互必須出現在超圖中.高階網絡上的傳播動力學受到了廣泛的關注.在高階網絡上的社會傳播中,研究發現高階結構會導致不連續相變與雙穩態區域,雙穩態區域中穩態規模依賴初始感染種子數目[30,32].在社會傳播模型的基礎上,研究人員提出了高階網絡上的多動力學耦合傳播模型,例如高階網絡上的競爭傳播與意識疾病耦合傳播等.相比于簡單圖上的競爭傳播[33],引入高階交互使兩種流行病可共存[34].意識疾病耦合傳播中,社交網絡中的高階交互可緩解低流行病傳播率下信息傳播不足的問題,有助于抑制流行病傳播[35].

簡單網絡與高階網絡間的傳播現象具有明顯差異,因此識別高階網絡上最有影響力傳播者的研究值得關注.度中心性、接近中心性、介數中心性和特征向量中心性等概念被擴展至單純復形,用于識別核心蛋白[36].類似地,特征向量中心性被推廣并應用于識別超圖中的重要節點與重要超邊,其主要思想為節點的重要性依賴于節點參與超邊的重要性,而超邊的重要性依賴超邊所包含節點的重要性[37].還有研究人員提出向量中心性以描述節點在不同尺寸超邊中的重要性[38].現有高階網絡中重要節點識別方法主要基于網絡結構,鮮有同時考慮網絡結構與傳播過程.

已有研究表明節點的傳播影響力由網絡拓撲結構與傳播過程共同決定.相比于僅使用網絡拓撲結構的方法,同時考慮傳播過程與網絡拓撲結構的方法能更準確地識別網絡傳播中最有影響力的傳播者[39,40].本文基于網絡結構與傳播過程,提出傳播中心性.首先提出單純復形上易感-感染-恢復(susceptible-infected-recovered,SIR)微觀馬爾可夫鏈方程組用于描述單純復形上的SIR 傳播動力學;接下來計算微觀馬爾可夫鏈方程組收斂時節點被感染的概率.節點被感染的概率由網絡結構與傳播過程共同決定,將其定義為 “傳播中心性” (spreading centrality,SC),用于排序節點的傳播影響力.在兩類合成網絡與4 個真實網絡上的大規模仿真實驗表明,傳播中心性與節點真實傳播影響力高度正相關.相比于高階網絡的度中心性、特征向量中心性以及簡單網絡上最優的集體影響中心性、非回溯中心性等基準中心性,本文提出的傳播中心性能更為準確地識別高階SIR 傳播中最有影響力的節點,排序準確性更高.

2 單純復形上的傳播模型

本節首先介紹單純復形的定義,再說明單純復形上的易感-感染-恢復傳播模型.單純復形定義為M=(V,C),其中,V表示節點集合,C表示單純形集合[30].k階單純形σ ?C表示k+1 個節點{v0,v1,v2,···,vk}組成的高階交互.單純復形中,0 階單純形表示單個節點,1 階單純形表示邊,2 階單純形表示“滿”三角面等.單純復形滿足以下條件,若單純形ω ?C,其所有子單純形v ?ω必須被包含在C中.如2 階單純形w={v0,v1,v2}?C,則{v0},{v1},{v2},{v0,v1},{v0,v2}和{v1,v2}?C.為了簡便,使用的單純復形中僅包含0 階單純形(節點),1 階單純形(邊)和2 階單純形(高階交互).

在單純復形上的SIR 傳播[41]中,個體可有3 種狀態: 易感態(susceptible,S),感染態(infected,I),或恢復態(recovered,R).在每個時間步,I 態個體以一定速率將S 態鄰居感染,并以一定速率自發恢復為R 態.單純復形上,沿著1 階單純形(連邊)和2 階單純形(三角面)都將發生感染事件.本模型的傳播參數為(β1,β2,μ),其中β1表示1 階單純形感染S 態成員的速率,β2表示2 階單純形感染S 態成員的速率,μ表示I 態個體的恢復速率.圖1展示單純復形上個體感染與恢復的過程,邊表示1 階單純形,“滿”三角面表示2 階單純形.圖1(a)—(j)中橙色邊表示S 態個體通過1 階單純形以速率β1被感染.圖1(h)中橙色“滿”三角面表示S 態個體通過2 階單純形以速率β2被感染.圖1(h)中,S 態個體不僅通過1 階單純形被感染,同時也通過2 階單純形被感染.注意,當且僅當2 階單純形中的兩個節點同時處于感染態時,2 階單純形才能感染其第3 個成員.圖1(j)中,3 個節點雖形成“滿”三角面,但其中只有1 個節點感染,流行病無法通過2 階單純形進行傳播.

3 傳播中心性

本節提出單純復形上的微觀馬爾可夫鏈方程組,通過微觀馬爾可夫鏈方程組計算動力學穩態時各節點被感染的概率,并將其定義為節點的傳播中心性.定義為t時刻節點i處于X狀態的概率,X ∈{S,I,R},如表示t時刻節點i處于S 態的概率.定義qi(t) 表示t時刻節點i沒有被1 階單純形感染的概率,有

其中,Γi表示包含節點i的1 階單純形集合.定義表示t時刻節點i沒有被2 階單純形感染的概率,有

其中,?i表示包含節點i的2 階單純形集合.節點i在t時刻未被感染的概率qi(t) 可定義為

節點i處于不同狀態概率隨時間t的演化方程組可寫為

(4)式表示節點i在t時刻處于S 態且未被感染,在t+1 時刻仍處于S 態的概率.(5)式右邊第1 項表示節點i在t時刻處于S 態且被感染,在t+1 時刻處于I 態的概率.右邊第2 項表示節點i在t時刻處于I 態且未恢復,在t+1 時刻仍處于I 態的概率.(6)式由節點處于S態,I 態與R 態的概率之和為1 的性質所得.

為了求解單個節點作為初始傳播源時,系統達到穩態后各節點被感染的概率,初始時設置=1-1/N,=1/N,=0,N為網絡中節點數目.迭代(1)—(6)式至收斂,獲得各節點被感染概率.將其定義為傳播中心性(spreading centrality,SC).流行病通過接觸傳播,疾病將優先到達擁有著更多接觸的個體,即表現出更高的被感染概率.一旦這些個體被感染,他們更有可能將流行病傳播出去,造成大規模感染.傳播中心性屬于迭代中心性,但與特征向量中心性等不考慮傳播過程的迭代中心性不同,傳播中心性加入了傳播過程,迭代過程與傳播過程一致.

4 仿真實驗方法

為了驗證傳播中心性識別最有影響力傳播者的準確性,我們在兩類合成網絡(勻質度分布網絡與異質度分布網絡)與4 個真實網絡上進行大量仿真實驗.本節首先介紹合成網絡與4 個真實網絡的生成方法,然后說明4 個用于比較的基準中心性及評價準確性的指標.

4.1 網絡構建方法

在實驗中使用了隨機單純復形與無標度單純復形兩種合成網絡.隨機單純復形模型(random simplicial complex,RSC)用于生成勻質度分布的單純復形[42].生成步驟如下: 以概率p1在任意兩節點間生成邊,再以概率p2在任意3 個節點間生成2 階單純形.p1,p2與節點平均關聯的1 階單純形數目〈k1〉,節點平均關聯的2 階單純形數目〈k2〉 之間關系如下:

無標度單純復形模型(scale-free simplicial complex,SFSC)用于生成異質度分布網絡[42].生成步驟如下: 以Barabási-Albert 模型生成無標度網絡,即每個新加節點按度偏好選擇m個舊節點生成連邊.然后以概率p2在任意3 個節點間生成2 階單純形.〈k2〉可由(8)式計算,〈k1〉 表示為

采用4 個面對面接觸數據集構建真實單純復形[43–46].這些數據集從不同的人群接觸場所中得到,包括工作場所(InVS15)、醫院(LH10)、會議(SFHH)與高中(Thiers13).每個數據集中,記錄了以20 s 為時間間隔的個體間面對面的交互.我們以5 min 作為時間窗口聚合數據.在一個時間窗口中,若兩個節點有面對面接觸則生成一條邊,即1 階單純形.3 個節點兩兩接觸則生成2 階單純形.統計邊與2 階單純形在所有時間窗口中出現的總次數,最后保留50%出現次數最多的1 階單純形與20%出現次數最多的2 階單純形用于構建真實單純復形.表1 展示了使用上述方法構建的合成單純復形與真實單純復形的簡單統計特征,其中N為網絡中節點數目,〈k1〉 為節點平均關聯的1 階單純形數目,〈k2〉 為節點平均關聯的2 階單純形數目,是流行病爆發時,1 階單純形傳播速率的閾值,通過計算機模擬所得.在后文實驗中,將1 階單純形傳播速率設置為該模擬閾值的1—2倍,以控制傳播規模.

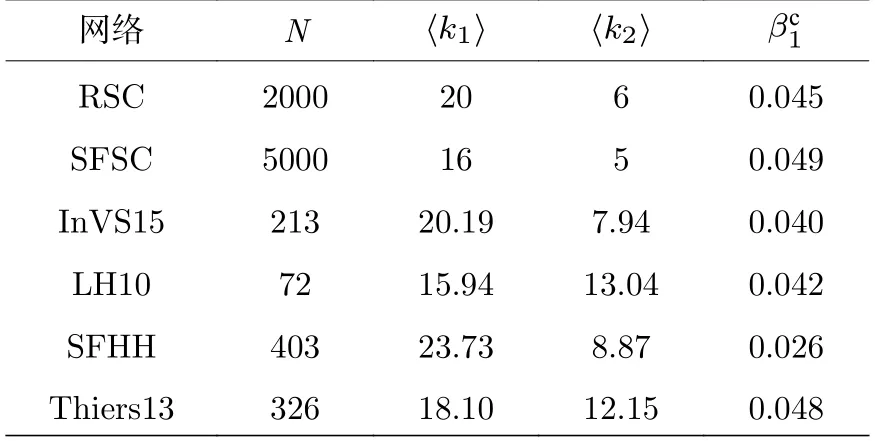
表1 合成與真實單純復形屬性Table 1.Properties of the synthetic and real simplicial complexes.

4.2 基準中心性

為了與本文提出的傳播中心性比較,我們選擇高階網絡的度中心性[31]與特征向量中心性[37],簡單網絡上當前最優的集體影響中心性[15]與非回溯中心性[21]作為比較的基準中心性.

高階網絡上的度中心性定義為節點直接鄰居數目或節點參與交互數目.本文采用節點交互數目的定義方式,則節點度中心性可寫為

其中,ki表示節點i參與1 階單純形的數目,表示節點i參與2 階單純形的數目.

超圖中節點與超邊的特征向量中心性(EVH)認為節點重要性依賴于節點所在的超邊,超邊重要性依賴于超邊所包含的節點,其數學定義為

式中,λ 和μ是比例常數.x,y是向量,xi表示節點i的特征向量中心性值,ye表示超邊e的特征向量中心性值.B是超圖的關聯矩陣,超邊e包含節點i,則Bie=1,反之Bie=0 .g,f,ψ,φ 是4 個映射函數,用于實現不同的依賴關系.本文中設定:

集體影響中心性(collective influence,CI)與非回溯中心性(nonbacktracking,NB)是簡單網絡上的最優中心性算法.集體影響中心性基于最優滲流,推導得出節點i的CI 中心性定義為

式中，ki表示節點i的度,?Ball(i,l) 表示與節點i距離為l的節點集合.本文計算集體影響中心性時設置l=2 .

非回溯中心性與標準特征向量中心性類似,但通過非回溯矩陣避免標準特征向量中心性的局部化問題.節點j的非回溯中心性定義為

其中,A表示簡單圖的鄰接矩陣,vi→j是簡單圖的非回溯矩陣的主特征向量中邊ei→j對應的分量.將簡單圖上的集體影響中心性與非回溯中心性算法用于單純復形時,我們不考慮單純復形中的高階交互(即“滿”三角面)的影響,即僅考慮網絡中的節點與連邊.

4.3 評價指標

為了評估不同中心性識別最有影響力傳播者的準確性,我們使用不準確函數[14]、肯德爾相關系數與Top-K準確率作為評價指標.不準確函數ξ(p)度量中心性識別最有影響力傳播者的不準確性,定義為

其中p是計算節點的比例(0 ≤p≤1).M(p) 表示規模為N的網絡中,中心性排序在前的pN個節點的平均傳播影響力,Meff(p) 表示真實傳播影響力排序在前的pN個節點的平均傳播影響力.ξ(p) 量化了實際最有傳播影響力的傳播者與中心性最高的傳播者間平均傳播影響力的接近程度.ξ(p) 越小,中心性在識別最有影響力的傳播者時越準確.

肯德爾相關系數用于度量兩個排序序列的相關性,定義為

Top-K準確率用于度量中心性對最有傳播影響力的前K個節點的識別準確性,定義為

其中,SK表示中心性值在前K的節點集合,表示真實傳播影響力在前K的節點集合,|SK| 表示集合SK中的元素數目.Top-K準確率越高表示中心性識別最有傳播影響力的節點越準確.

5 實驗結果

我們在合成網絡與真實網絡上度量傳播中心性SC 排序節點影響力的性能.首先,分析了節點傳播中心性與傳播影響力的相關性,如圖2 所示.結果表明,節點傳播中心性與傳播影響力高度正相關.當β1=時,RSC 網絡上節點傳播中心性與傳播影響力的皮爾遜相關系數為0.9691;當β1=時,皮爾遜相關系數分別為0.9887 與0.9910.其他網絡上,結果與RSC 網絡中類似.實驗中,為了獲得單個節點的傳播影響力,對單純復形上的SIR 傳播模型進行大規模的蒙特卡羅模擬.初始時,將節點i設置為感染態,其余節點設置為易感態,統計傳播達到穩態時網絡的感染規模,即恢復態占比.獨立重復上述模擬 103次,將感染規模的均值作為對節點i的真實傳播影響力Si的估計.當系統初始狀態確定時,微觀馬爾可夫鏈方程組的收斂狀態是固定的,不具備隨機性.我們設置(t=0)=1-1/N,(t=0)=1/N,(t=0)=0,通過迭代微觀馬爾可夫鏈方程組計算傳播中心性.在實驗中,固定恢復速率μ=1,通過改變傳播速率β1與β2設定不同的有效傳播速率.μ的取值僅影響傳播的時間演化尺度,不影響實驗結果.

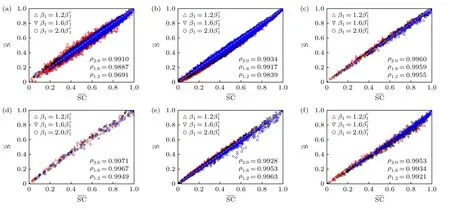
圖2 節點傳播中心性與傳播影響力的散點圖.SC與S 分別表示歸一化后的節點傳播中心性與傳播影響力(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.2.Scatter plots of the spreaing centrality and spreaing influence of nodes.SC and S represent the normalized spreading centrality and spreading influence of nodes: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.

為了考察提出的傳播中心性SC 排序節點傳播影響力的準確性,采用不準確函數作為評價指標.不準確函數值越低,該中心性識別最有影響力的傳播者越準確.如圖3 所示,傳播中心性能準確有效地識別最有影響力的傳播者.在所有網絡上,傳播中心性的不準確函數低于0.02,傳播中心性多數情況下優于其他基準中心性.在SFSC 與Thiers13網絡中,傳播中心性明顯優于所有基準中心性.在RSC 網絡上,傳播中心性略優于集體影響中心性、特征向量中心性與非回溯中心性,明顯優于度中心性.在InVS15 網絡中,當0

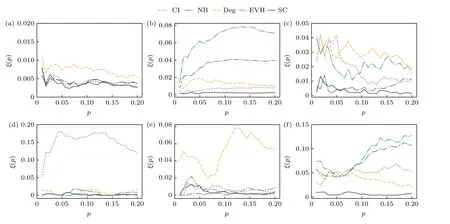
圖3 各中心性的不準確函數(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13 Fig.3.Imprecisions of the centralities: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.

為了考察傳播參數改變時,提出的傳播中心性的性能,對比了不同1 階單純形傳播速率下各中心性與節點傳播影響力的相關性,如圖4 所示.結果表明,在所有網絡中,所提的傳播中心性與傳播影響力的肯德爾相關系數大于基準中心性與傳播影響力的肯德爾相關系數.合成網絡中傳播中心性的肯德爾相關系數隨1 階單純形傳播速率的增大而增大.在RSC 網絡中,傳播中心性在1 ≤α≤1.4時略優于特征向量中心性、非回溯中心性和集體影響中心性,明顯優于度中心性.當1.4<α≤2 時略優于集體影響中心性,明顯優于其余中心性.SFSC網絡中,傳播中心性明顯優于其他基準中心性.真實網絡中結果與合成網絡結果類似.在InVS15 與Thiers13 網絡中,傳播中心性明顯優于其他基準中心性.在LH10 與SFHH 網絡中,傳播中心性略優于非回溯中心性,明顯優于集體影響中心性,特征向量中心性與度中心性等基準中心性.其余傳播參數設置如下: 恢復速率μ=1,1 階單純形傳播速率β1=.2 階單純形傳播速率設定為β2=0.1 .實驗中設置1 階單純形傳播速率β1∈.當β1<時,流行病不能爆發,所有節點的傳播影響力接近于0;當β1>時,傳播速率過大,所有節點都會導致較高的流行病爆發規模.傳播速率過小或過大都無法充分地體現節點間傳播影響力的差異.基本再生數度量感染節點感染下一代節點的能力,是傳播中的一個重要參量.復雜網絡SIR 傳播模型基本再生數定義為R0=(k+s2/k)β/μ,其中β 是傳播速率,μ是恢復速率,k是平均度,s是度分布的標準差.實驗中,設置1 階單純形傳播速率β1∈,此時各網絡的基本再生數取值范圍為: RSC [0.98,1.96];SFSC [1.06,2.12];InVS15[0.97,1.94];LH10 [0.97,1.94];SFHH [0.99,1.98];Thiers13 [1.05,2.10].由于流行病主要通過邊進行傳播,高階作用僅起強化作用,我們計算R0時未考慮高階作用.

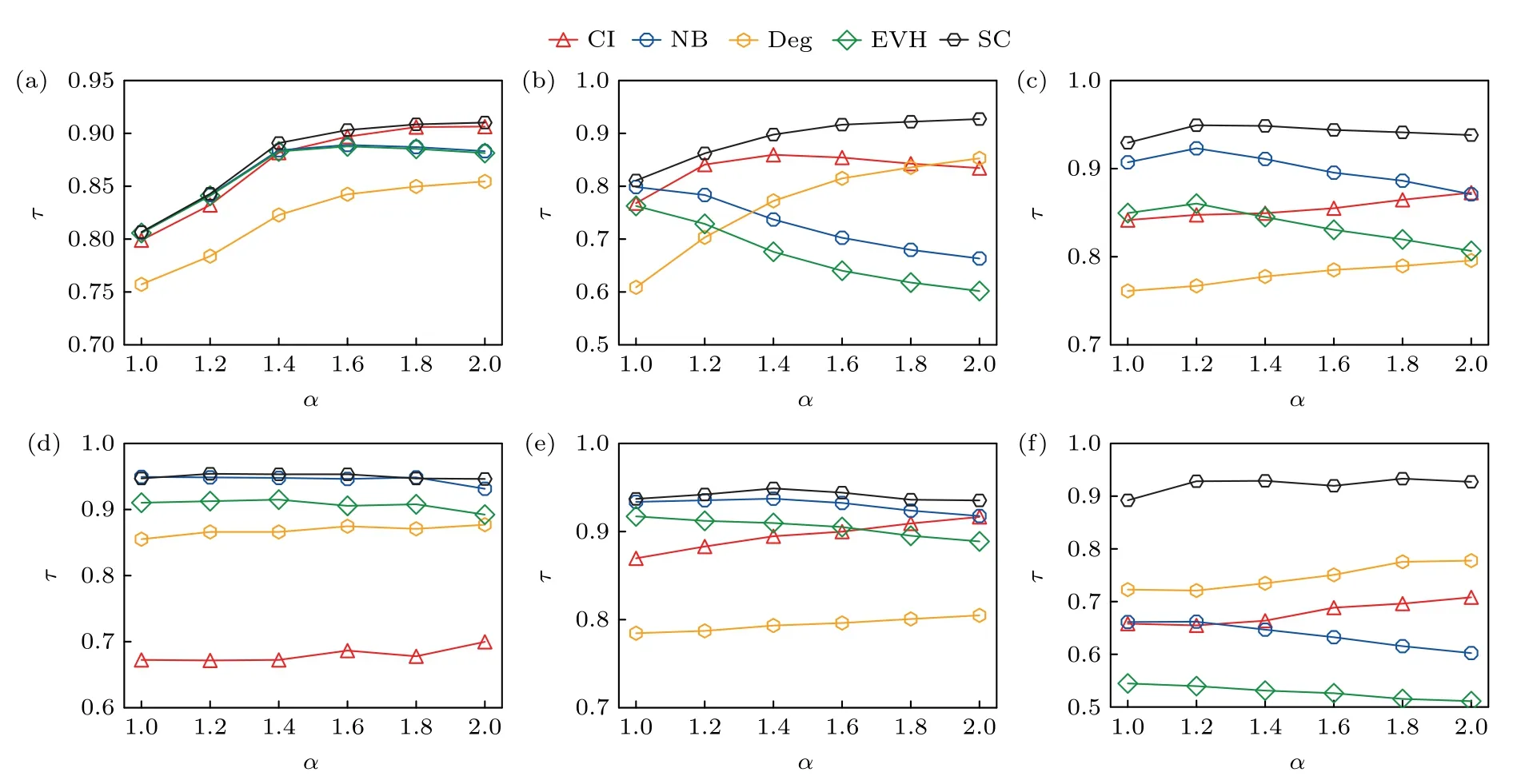
圖4 不同1 階單純形傳播速率 β1=下,節點各中心性與傳播影響力的肯德爾相關系數(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.4.Kendall’s tau correlation of the centralities and the spreading influence of nodes under different 1-simplex spreading rates β1=: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.

在高階網絡傳播中,2 階單純形傳播速率會影響節點的傳播影響力.我們改變2 階單純形傳播速率β2,考察中心性與節點傳播影響力的相關性.如圖5 所示,在合成網絡和真實網絡中,多數情況下傳播中心性SC 與節點傳播影響力的相關性最高.在合成網絡RSC 與SFSC中,傳播中心性的肯德爾相關系數基本不隨β2變化且優于基準中心性.在真實網絡InVS15,LH10 與SFHH中,傳播中心性的肯德爾相關系數隨β2的增大呈現下降趨勢.在Thiers13 中傳播中心性的肯德爾相關系數變化趨勢平坦.與基準中心性相比,InVS15 與Thiers13網絡中傳播中心性完全優于其他基準中心性.在LH10 網絡中,當0 ≤β2≤0.1時,傳播中心性優于所有基準中心性,當0.1<β2≤0.2 時傳播中心性略差于非回溯中心性但優于其他基準中心性.SFHH網絡結果與LH10 類似,當0≤β2<0.15 時傳播中心性優于所有基準中心性,而當0.15≤β2≤0.2 時傳播中心性略差于非回溯中心性但優于其他基準中心性.當β2=0時,2 階單純形不再傳播流行病,高階網絡上的傳播退回到普通網絡上的SIR傳播模型.此時,節點的傳播中心性與傳播影響力間的肯德爾系數接近或高于0.9,明顯優于普通網絡上性能最優的集體影響中心性與非回溯中心性.隨著2 階單純形傳播速率β2增大,傳播中心性與傳播影響力間的相關性呈現出小幅降低的現象.當傳播發生在2 階單純形上時,節點感染與被感染過程是非對稱的.若2 階單純形中僅有一個節點處于感染態,該單純形無法傳播流行病,即一個節點容易通過2 階單純形被感染不代表它容易通過2 階單純形傳播流行病.隨著2 階傳播速率β2增大,這種非對稱性帶來的負面效果將會升高,傳播中心性與傳播影響力間的相關性將小幅降低.在圖5 的實驗中,其余傳播參數設置為:β1=,μ=1 .

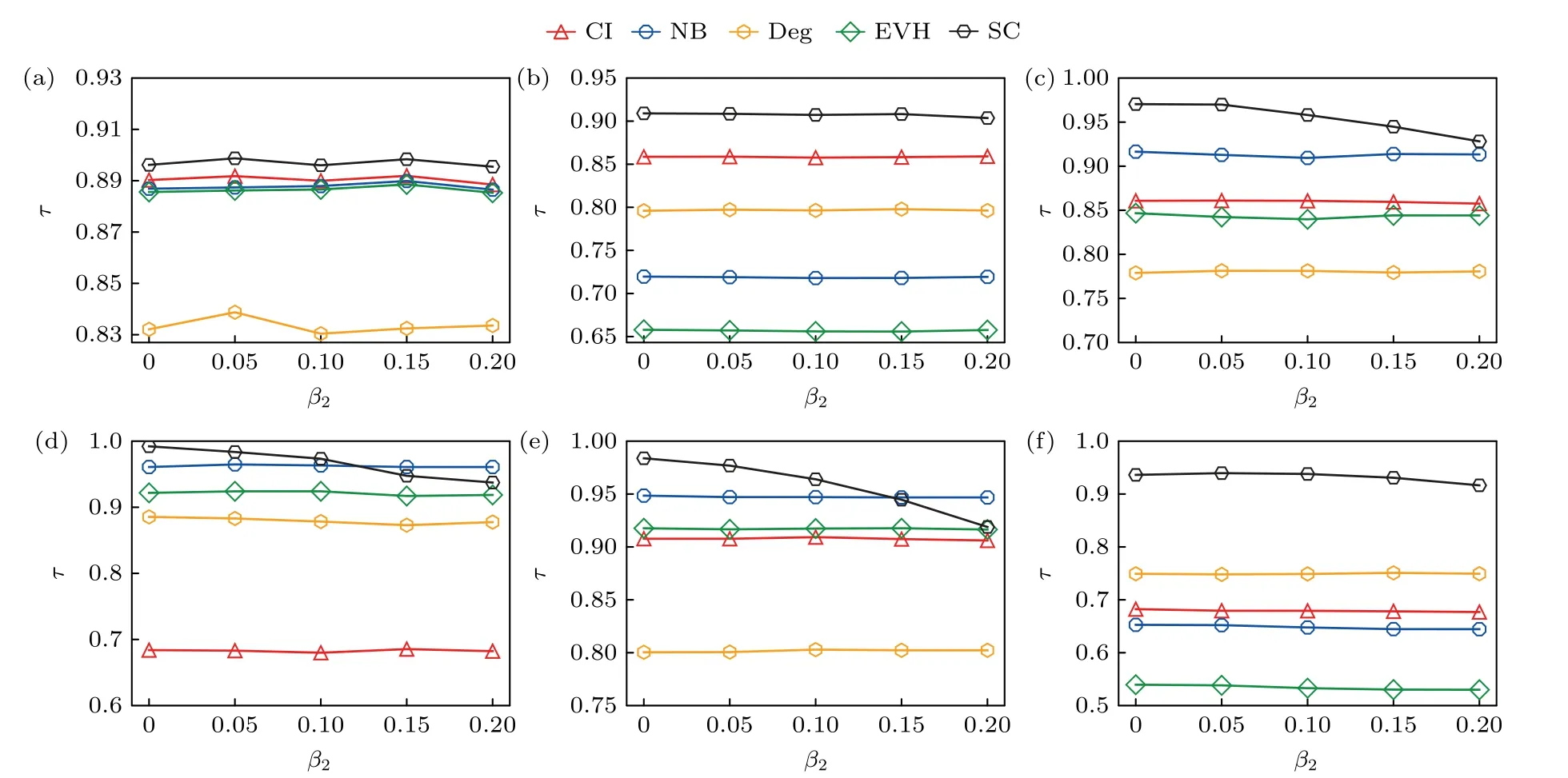
圖5 不同2 階單純形傳播速率 β2下,節點各中心性與傳播影響力的肯德爾相關系數(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.5.Kendall’s tau correlation of the centralities and the spreading influence of nodes under different 2-simplex spreading rates β2 : (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.

最后,通過Top-K準確率表征各中心性對前K個最有傳播影響力節點的識別準確率.表2 展示了各中心性的Top-10,Top-20 與Top-30 準確率.綜合來講,傳播中心性多數情況下能較為準確地識別前K個最有影響力的傳播者.當K=10時,在RSC,InVS15,SFHH 與Thiers13 網絡中,傳播中心性有著最高的Top-10 準確率,即在識別前10 個影響力最大的節點時,傳播中心性SC 準確率最高.當K=20時,在除SFSC 網絡外的其他網絡中,傳播中心性有著最高的Top-20 識別準確率.當K=30時,傳播中心性在SFSC,LH10 與Thiers13網絡中有著最高的Top-30 識別準確率.Thiers13網絡中,傳播中心性有著最高的Top-K準確率,且明顯高于所有基準中心性的Top-K準確率.傳播參數設置如下:β1=,β2=0.1,μ=1 .

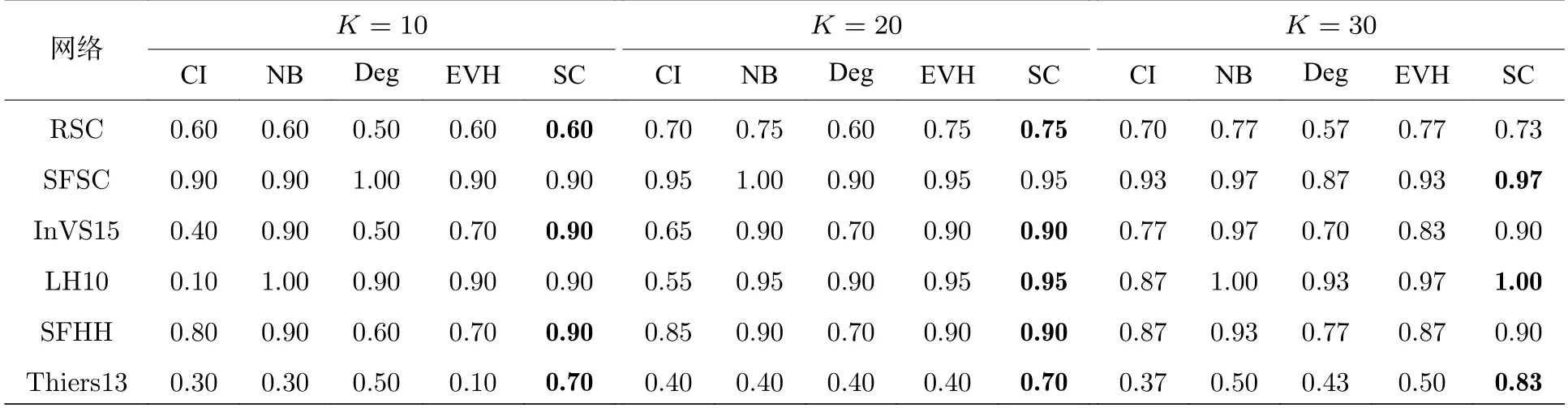
表2 各中心性的Top-K 準確率Table 2.Top-K accuracy of centralities.

6 結論

識別網絡傳播中最有影響力的傳播者是控制傳播過程的關鍵步驟之一.本文研究高階網絡上SIR 傳播過程中最有影響力傳播者的識別方法.我們提出單純復形上SIR 微觀馬爾可夫鏈方程組,用于描述SIR 傳播動力學過程.利用微觀馬爾可夫鏈方程組,計算單源傳播時各節點被感染的概率,定義度量節點傳播影響力的指標,傳播中心性.大量仿真實驗表明,傳播中心性與節點真實傳播影響力高度正相關.相比于4 種基準中心性,即高階網絡上的度中心性、特征向量中心性等僅考慮網絡結構的中心性與復雜網絡上最優的集體影響中心性、非回溯中心性,本文提出的傳播中心性在兩類合成網絡中識別傳播重要節點時比基準中心性更準確,在真實網絡中多數情況下優于基準中心性.傳播中心性方法可以擴展到超圖上.對于超圖上的傳播,可以類似地寫出描述傳播動力學的微觀馬爾可夫鏈方程組,再利用該方程組計算節點的傳播中心性.

傳播中心性具有一定局限性.通過節點被感染概率預測節點的真實傳播影響力時,假設越容易被感染的個體越容易感染鄰居,即感染與被感染是對稱的.考慮感染與被感染的方向性,當傳播發生在1 階單純形上時,感染與被感染是對稱的;當傳播發生在2 階單純形上時,2 階單純形中單個感染態節點并不能通過該2 階單純形傳播流行病,感染與被感染是非對稱的.感染與被感染的非對稱性會降低傳播中心性的排序準確性,考慮2 階單純形上的非對稱性可以進一步提升傳播中心性的準確性.當感染與被感染的對稱性受到嚴重破壞時,傳播中心性可能不再適用.例如傳播在有向網絡上發生時,傳播中心性可能不再準確.因此,未來需要進一步探索如何在有向網絡上識別最有影響力的傳播者.