立足“一以貫之” 實現“數學相通”
——以“多邊形的內角和、外角和的證明”為例
? 江蘇省南京市將軍山中學 張 俊
1 引言
對于多邊形內角和、外角和的內容,筆者一直頗有興致,尤其是相關結論的證明更需“一以貫之”.于是筆者嘗試將相關結論的證明過程進行有機整合,達到證明方式與思考路徑的“一以貫之”,讓學生對本部分內容進行內化并追本溯源,全面審視所學知識,提高立足點,關注知識的形成過程,達到將知識融會貫通的目的,讓學生在知識、思想與方法上實現“一以貫之”[1].
2 教學過程設計
問題1如何證明“三角形內角和是180°”?
追問1:問題1的這些證明方法,有什么共同點?
追問2:拼接點除了頂點處,還可以在哪里?
設計意圖:幫助學生回憶三角形內角和的證明本質,即借助平行線將三個內角拼成平角或同旁內角(如圖1~3).而構成平角的拼接點可以在頂點處,也可以在邊上、內部或外部(如圖4~6)[2].

圖1

圖2
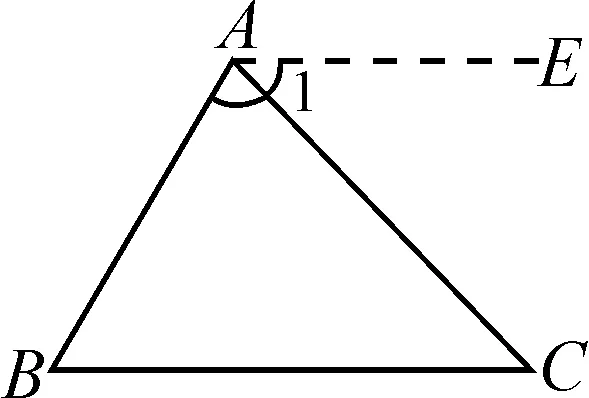
圖3

圖4

圖5

圖6
問題2關于點的位置的選擇問題,你有過類似的經驗嗎?
追問1:如何得到多邊形的內角和公式?
追問2:你有什么猜測?
設計意圖:借由此問,幫助學生明確多邊形內角和定理證明的本質,就是把多邊形變成若干個三角形.而分割線可以過頂點,也可以過邊上、內部、外部的任意一點進行分割(如圖7~10).通過追問,引發學生對多種方法證明外角和定理的思考.

圖7

圖8

圖10
問題3根據已有經驗,對于證明“三角形的外角和是360°”,你準備如何開展研究?
設計意圖:幫助學生根據已有經驗,從周角入手,明確三角形外角和的證明其本質就是把外角拼接到一起轉化為一個周角.因此,構造周角的點P既可以置于三角形的頂點處,也可以置于三角形的邊上、內部和外部.(如圖11~14)
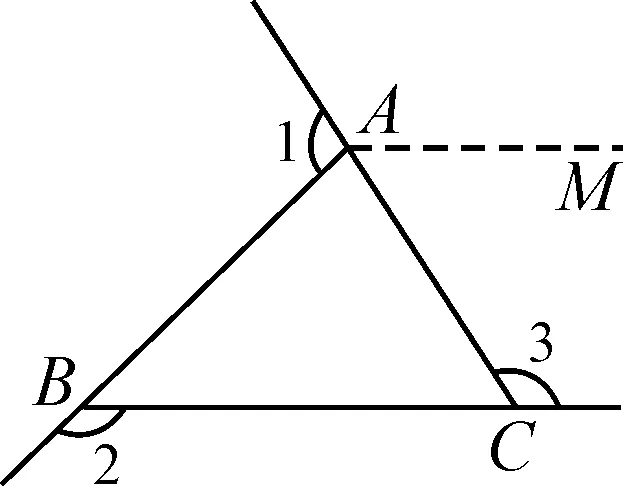
圖11

圖12

圖13
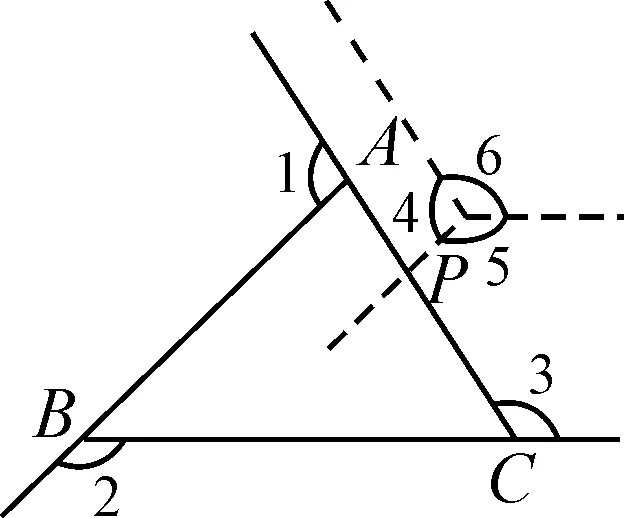
圖14
追問1:接下來你準備如何繼續開展研究?
追問2:如何證明“多邊形的外角和為360°”?
設計意圖:類比之前的學習,學生可以熟練地利用平行線,將各外角進行平移、拼接.而拼接點的位置自然可以在頂點、邊上、內部、外部等位置.
問題4通過對內角和與外角和結論證明方法的梳理,你有哪些感受?
設計意圖:在梳理中,讓學生感覺到證明方法雖然多樣,但關鍵都是如何平移角的問題.方法雖然很豐富,但平移角的時候,輔助線都不太好添加.
追問:為了讓證明更具簡潔美,可以從復雜圖形中尋找出簡潔的基本圖形,請試著找一找.
設計意圖:幫助學生找到這個不變的基本圖形,可稱為“移動的平角”.同樣地,在三角形的外角和證明過程中,也存在這樣一個不變的圖形,那就是“移動的周角”.(如圖15~16)

圖15
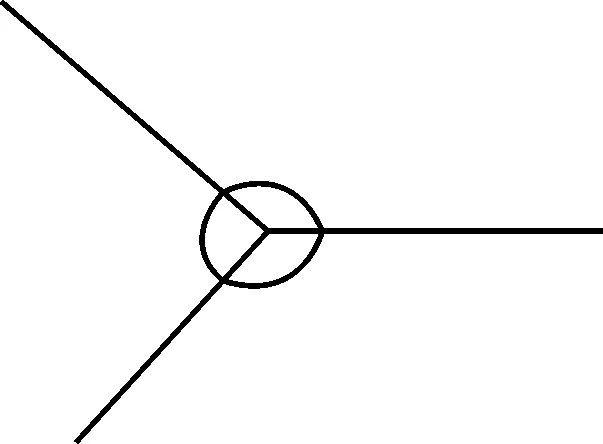
圖16
問題5能否設計一個轉筆游戲,來驗證內角和與外角和的大小呢?
設計意圖:設計轉筆游戲,可讓學生結合轉動的位置判斷屬于內角和(如圖17)還是外角和(如圖18),再根據轉動后筆尖的方向判斷轉動的度數,驗證旋轉角度的類別和大小.

圖17

圖18
問題6通過今天的學習,你對多邊形的內角和與外角和有哪些新的認識?
設計意圖:通過總結與反思,學生感受到有關內角和與外角和的證明在本質、思路與技巧上的一致性,體會數學知識的相通性,從而實現學習數學的“一以貫之”.
3 教學思考
本節課將三角形的內角和、外角和,多邊形的內角和、外角和相關結論的證明過程進行有機整合,實現了“一以貫之”的目標,關注知識的形成過程和發生發展過程,以生為本,順其自然,循循善誘,水到渠成.
3.1 有效整合,一以貫之
教材依托實驗獲得新知,內容看似簡單,實際知識豐富,如果只按教材授課,那么學生的思維發展會比較局限.筆者將相關知識有機整合,讓學生厘清內在關系,站在更高的立足點上去觀察問題,將很多問題融會貫通,達到了有效整合的目的.不同的證明方法之間也有著內在的聯系,而這些聯系最終將回到平角、周角等知識上去,體現了證明方法的“一以貫之”,引領學生從“學會”到“會學”.
3.2 問題驅動,一以貫之
本課的設計采用“問題驅動、一以貫之”的教學方式,利用問題逐步引導,創造一種具體問題情境讓學生發現問題、解決問題,促進思維發展.
利用問題引導學生思考三角形內角和的證明方向和本質,嘗試思考輔助線的不同添加方式.再利用問題讓學生體會多邊形內角和公式與其他結論的證明思路一致之處.同時,通過追問再將其思路引入到三角形外角和結論的證明當中,顯得自然流暢.
通過問題,學生感受到三角形外角和、多邊形外角和相關結論的證明就是將這些外角拼接成一個周角,體會數學的“一以貫之”的類比思想.
3.3 層層突破,一以貫之
教學的核心就是“教學設計”.本節課抓住了教學活動中學生的三次突破,層層推進教學.
第一次突破在問題1:拼接點除了頂點處,還可以在哪里?事實上,這一教學環節的關鍵就在引出“轉化”的數學方法.有了這個環節方法的研究,后續研究多邊形的外角和就可“一以貫之”了.
第二次突破在問題3:“外角和是否也可以用這樣的方法證明呢?”這既是數學本身發展的需要,更是滿足學生的探究欲望的需要,這一環節的探究就顯得很開放,學生的自主地位很明顯.
第三次突破在問題5:當完成了所有的研究后,并不能體會它的價值.此時轉筆實驗應運而生.在實驗中,讓學生嘗試將筆端放在邊上、外部進行旋轉,用實驗體會證明方法的“一以貫之”.
數學本身就是相通的,只有立足“一以貫之”,實現“數學相通”,才能更好地幫助學生將數學知識、數學方法與數學思想融合,帶領學生站在數學的山頂俯瞰數學,欣賞數學!

