“動”中求“靜”,“動”“靜”互化
——中考動態幾何問題解題思路初探

? 江蘇省蘇州市高新區實驗初級中學 袁 媛

馬克思主義哲學告訴我們,運動是絕對的,靜止是相對的.在幾何的學習過程中,我們發現“靜”只是“動”的瞬間,是運動的一種特殊形式,“動”與“靜”是可以相互轉化的.如果能讓靜止的幾何圖形“動”起來,就可以幫助學生加深對圖形概念的準確理解,探索圖形的性質.教師可以用動態圖形創設富有啟發性的教學情境,引發學生對問題的討論與思考;還可以通過動態圖形讓學生體驗數學實驗成功的樂趣.更重要的是,動態的幾何圖形能夠把與幾何、代數相關的知識聯系起來,其中蘊含著動靜結合、數形結合的思想方法,能夠在運動變化中發展學生的空間想象能力,不斷提高學生綜合分析、解決問題的能力.

在初中幾何教學中,與動態圖形有關的問題主要有以下幾類.

1 動“點”類問題

動點問題是中考數學中最常見的題型,涉及面非常廣泛.解決動點類問題的思路是化動為靜,以相對靜止的瞬間去尋求量與量之間的關系.

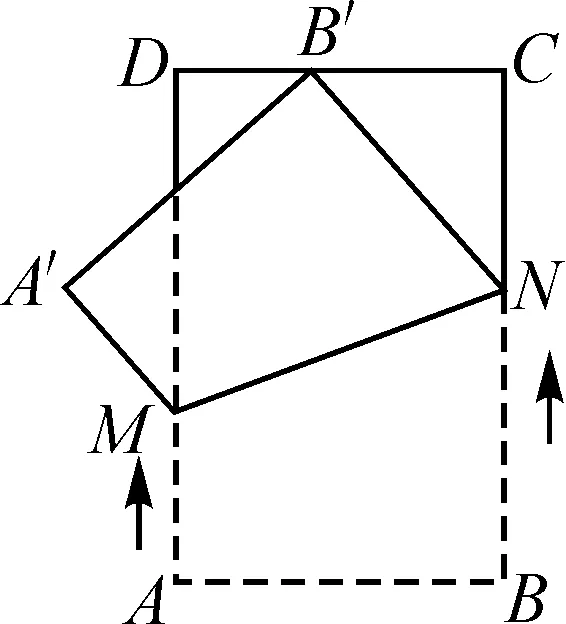
圖1

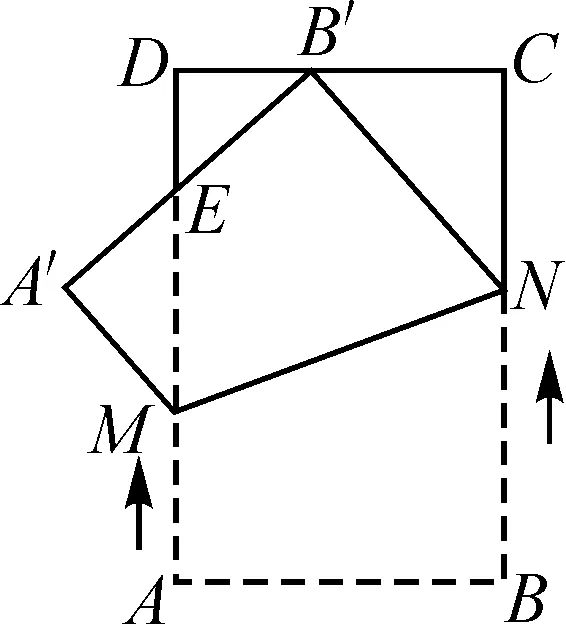
圖2

所以△A′EM≌△DEB′(ASA),則A′M=B′D=a,即AM=v1t=a.

思路與方法：本題考查矩形背景下的動點問題,通過動態圖形,將矩形的性質、對稱性質、中點性質、三角形相似、全等的判定與性質、勾股定理及翻折的運動形式等知識點聯系起來.熟練掌握相關性質及三角形全等的判定定理,利用翻折及中點性質,根據三角形全等的性質求出相應線段的長是解題的重要方法.

2 動“線”類問題

動線類問題的特點很明顯,動線在運動過程中可能會出現多種情況,盡管情況不同,但解題的思路是一致的,那就是“以靜制動”,通過特殊的靜止狀態去尋找量之間的關系.

例2(2022年江蘇省鹽城市中考第14題)如圖3,在矩形ABCD中,AB=2BC=2,將線段AB繞點A按逆時針方向旋轉,使得點B落在邊CD上的點B′處,線段AB掃過的面積為______.

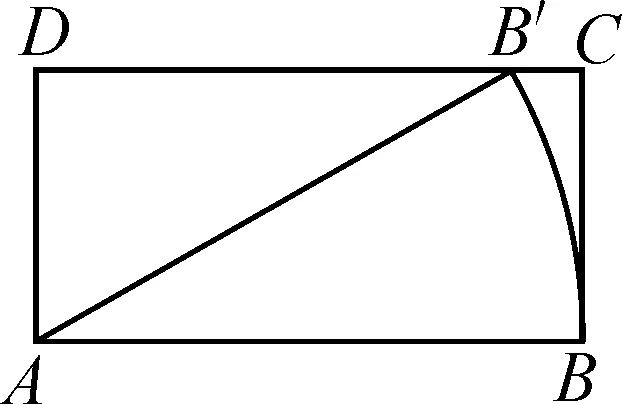
圖3

解析：由AB=2BC=2,得BC=1,所以AD=BC=1.因為將線段AB繞點A按逆時針方向旋轉,所以AB′=AB=2.

思路與方法：首先由動線AB旋轉的性質可得AB′=AB=2,再由銳角三角函數可求出∠DAB′=60°,進而求出∠BAB′,最后根據扇形面積公式即可獲解.本題考查了旋轉的性質、矩形的性質、扇形的面積公式、銳角三角函數等相關知識點.會觀察和分析動態圖形,靈活運用相關性質是解題的關鍵.

3 動“圖”類問題

動圖類問題常常結合圖形的平移、旋轉、翻折等變換,提出相關問題.解題的思路主要是從尋找圖形運動的特殊情況中打開,進而靈活運用相關幾何知識(如平行四邊形的性質、切線的性質、圓的有關知識、銳角三角函數、直角三角形等)解決問題.

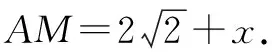
圖4

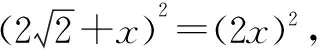
在△AME中,根據勾股定理,可得

第二種情況:當ED逆時針旋轉60°得到EF時,如圖5,作EM⊥AC交AC于點M.

圖5

在△AME中,根據勾股定理,可得

思路與方法：首先要考慮到圖形順、逆兩種旋轉情況,根據旋轉的性質可知△DEF是等邊三角形,過點E作EM⊥AC,又可證得△AEM是等腰直角三角形,再設DM=x,利用勾股定理便可求出x的值,最后利用勾股定理即可求出AE的長度.本題考查了圖形旋轉的性質、等邊三角形的判定與性質、勾股定理等知識點.能夠根據題意,按照ED順時針旋轉與逆時針旋轉兩種情況,分別畫出動態圖形進行分類解析是解題的關鍵.

綜上所述,解決動態幾何問題的基本思路是:把握運動規律,尋求運動中的特殊位置,在“動”中求“靜”,在“靜”中探求“動”的普遍規律.在具體解題過程中,要用運動與變化的眼光去觀察和研究圖形,把握圖形運動與變化的全過程,找出其中的等量關系和變量關系,并要特別關注一些不變量和不變關系或特殊關系.在解答動態幾何類題型時,經常要用到數形結合思想、分類思想、轉化思想和方程思想等重要的思想方法.