基于改進粒子群優化算法的多無人機協同欺騙干擾技術

劉宇蕊,陳云陽,余 鑫

(中國船舶集團有限公司第七二三研究所,江蘇 揚州 225101)

0 引 言

在現代電磁頻譜作戰環境中,利用多架無人機協同干擾的方式對組網雷達進行航跡欺騙已成為近年來新的作戰趨勢[1-2]。為了使得欺騙干擾效果顯著,無人機協同產生的假目標欺騙航跡需要滿足組網雷達“同源檢驗”的規則,這就需要對無人機的飛行任務進行合理的優化,完成航跡欺騙的同時也符合自身的飛行約束條件。多無人機協同欺騙干擾組網雷達系統問題通常為非連續、多參數以及多約束問題,故在優化時往往需要利用群體智能算法進行求解。為了有效地對組網雷達實施干擾,文獻[3]根據航跡欺騙干擾原理和無人機任務特點,對無人機實施航跡欺騙干擾模型進行了簡化,并給出了模型求解流程。文獻[4]研究了多機協同復合干擾航路規劃方法,該方法提高了在雷達組網環境下假目標航跡的可信度。文獻[5]采用最優化方法建立了多無人機協同干擾組網雷達的最優控制模型,并且利用最少數量的無人機完成了對組網雷達的欺騙。

粒子群優化算法(PSO)作為群體智能算法的典型代表,由于算法本身搜索速度快且易于實現,在處理大規模優化問題時可克服傳統數值求解方法求解速度慢、占用大量計算資源等問題,因而被有關學者提出并運用在實際的工程優化領域[6]。然而標準粒子群算法存在早期收斂速度過快、算法求解效率低等問題,為了得到更好的優化結果,本文在標準粒子群算法的基礎上設置了隨機慣性權重,增加了擾動粒子更新機制,提出了一種改進粒子群優化算法(IPSO)。利用改進后的粒子群優化算法以及標準粒子群優化算法分別對多機協同欺騙干擾數學模型進行優化,分析并比較改進粒子群算法和標準粒子群算法在優化求解多機協同干擾模型的差異性。

1 多機協同航跡欺騙干擾原理

多無人機協同航跡欺騙干擾主要考慮多架無人機對組網雷達系統的協同干擾問題,在組網雷達系統中,真實目標與有源假目標在空間狀態上存在顯著差異,利用組網雷達真假目標空間狀態差異來識別虛假目標的方法被稱為“同源檢驗”,它是組網雷達系統識別真假目標的理論基礎[7-8]。組網雷達系統信息融合中心基于一定的“同源檢驗”融合規則,對接收到的多部雷達在統一坐標系下的同一空間位置上檢測到的目標信號,判斷其是否為一個合理的目標航跡點,多個連續的合理目標航跡點就形成了目標航跡。圖1為多無人機協同對組網雷達進行航跡欺騙的示意圖。

圖1 多無人機協同對組網雷達航跡欺騙示意圖

2 無人機航跡動力學優化問題

本文將多機協同航跡欺騙干擾抽象為無人機航跡動力學優化問題,并建立了無人機航跡優化數學模型、約束條件以及對應的目標優化函數。本文假設組網雷達系統共有5部雷達,每部雷達的數據更新率為10 s,并規定只要3部或3部以上雷達檢測到的航跡點狀態信息在統一的坐標系中一致,則融合中心便認為該航跡點合理,并假設20個連續的航跡點便能在融合中心建成一條航跡。

2.1 模型假設

假設一：無人機的雷達散射截面積較小且具有較強的隱身能力,被組網雷達系統檢測到的概率可以忽略,并且同一時刻1架無人機只能干擾1部雷達。

假設二：無人機的飛行速度、飛行高度、最大加速度、轉彎半徑以及無人機間距均控制在合理的范圍內。

假設三：組網雷達系統中各部雷達的最大作用距離均為150 km,無人機進行航跡欺騙時需產生1條預先設定的干擾航跡,并且干擾總時長假定為200 s。

2.2 數學模型

圖2為無人機產生欺騙干擾航跡的數學模型示意圖,根據“同源檢驗”要求,虛假航跡上的每個點處均有至少3條雷達—無人機延長線相交。當虛假航跡點與其對應的3部雷達確定時,若無人機的飛行高度已知,則可根據幾何關系計算無人機在統一空間坐標下的位置坐標。

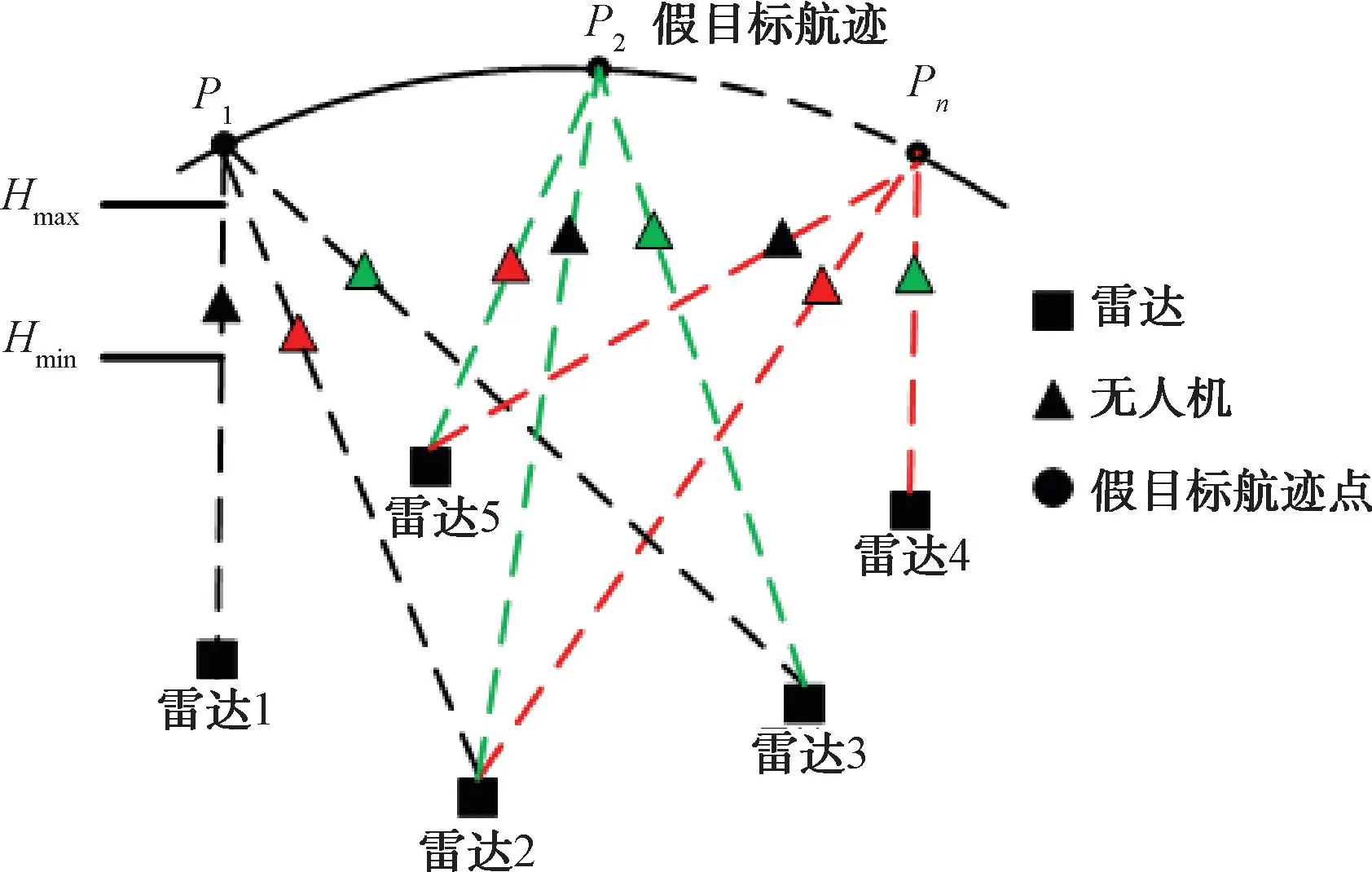
圖2 無人機產生欺騙干擾航跡數學模型示意圖

2.3 約束條件及目標函數

(1) 無人機飛行速度v、高度h滿足：120≤v≤180 km/h,2 000 m≤h≤2 500 m;

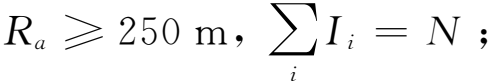
綜上所述,本文建立的多無人機協同航跡欺騙目標優化函數如下：

(1)

3 改進粒子群優化算法及模型求解

3.1 標準粒子群優化算法

標準粒子群優化算法源于對鳥群捕食行為的研究,對于每個目標函數優化的解都被看作為解空間中的一個粒子,在尋優過程中每個粒子都能得出一個優化問題解。假設xi=(xi1,xi2…,xiD)為第i個粒子(i=1,2,…,N)的D維位置參數;vi=(vi1,vi2…,viD)為第i個粒子的速度參量;pi=(pi1,pi2…,piD)為第i個粒子在空間中單獨搜尋的最優解;pg=(pg1,pg2…,pgD)為所有粒子在空間中搜尋到的最優解;粒子更新速度和位置參數如下：

vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+

c2r2(pgd-xid(t))

(2)

xid(t+1)=xid(t)+vid(t+1)

(3)

式中：ω為慣性權值;i=1,2,…,N;d=1,2,…,D;t表示當前迭代的次數;r1和r2均為介于(0,1)的隨機數;c1和c2稱為學習因子。

3.2 改進粒子群優化算法

(1) 設置隨機慣性權重

由式(2)可知：標準粒子群優化算法中的慣性權重在整個迭代過程中其值通常保持不變。若該參數設置過小,則會導致在算法前期不利于全局搜索,減少了種群的多樣性;若該參數設置過大,則會導致算法后期不利于局部探索,從而降低收斂速度。本文對固定慣性權重作了改進,設置了隨機慣性權重,不僅能夠加強算法前期的局部搜索能力,還能避免算法在迭代后期全局搜索能力不足。具體公式定義如下：

ω=ωmin+(ωmax-ωmin)ε1+με2

(4)

式中：ωmin與ωmax分別為隨機慣性權重的最小值和最大值;ε1為介于(0,1)均勻分布的隨機數;ε2為正態分布的隨機值;μ為符合擾動項的標準差,用來度量隨機變量權重ω與其數學期望之間的偏離程度。

(2) 增加擾動粒子更新機制

在標準粒子群優化算法迭代過程中,由于每個粒子只共享種群中最優粒子的信息,這種共享機制會使算法陷入局部收斂,不利于粒子在后期進行大范圍的搜索。針對上述問題,本文在標準粒子群優化算法的基礎上增加了擾動粒子更新機制,以保持種群的多樣性,使得粒子在移動方向上增加了更多的可能性,從而擴大了粒子的尋優空間。增加擾動粒子的速度更新公式如下：

vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+

c2r2(pgd-xid(t))+c3(r3-0.5)

(5)

式中：ω為慣性權重,其值由式(4)表示;c1和c2為學習因子,c3為擾動因子;r1和r2均為介于(0,1)的隨機數;r3為介于(-1,1)的均勻分布隨機數。

3.3 基于改進粒子群優化算法的求解步驟

利用改進粒子群優化算法對多機協同欺騙干擾模型進行求解的步驟如圖3所示。

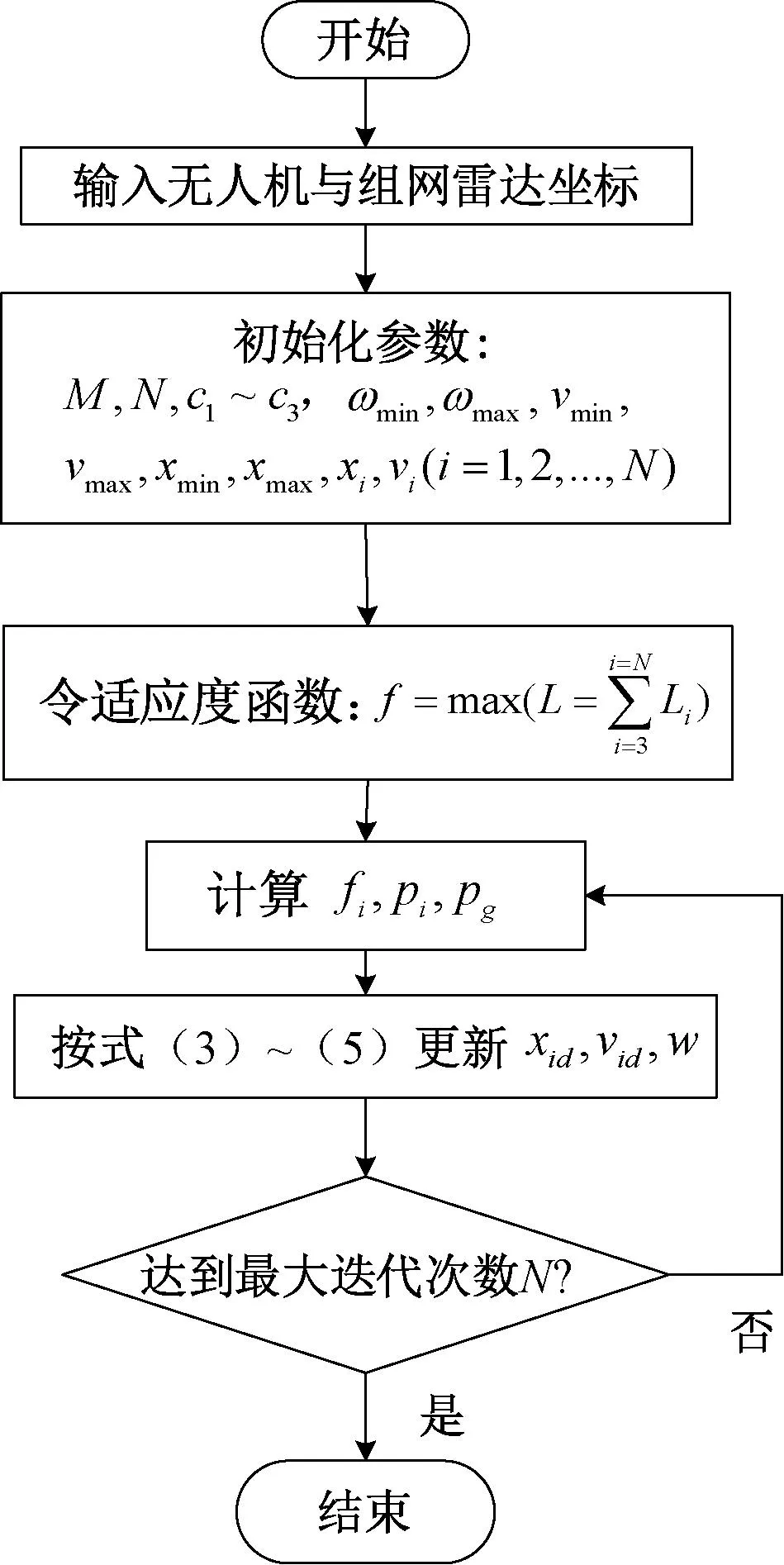
圖3 基于改進粒子群優化算法求解步驟流程圖

4 仿真結果與分析

4.1 仿真實驗參數設置

本文的仿真實驗環境為Matlab R2018b,假設某組網雷達系統5部雷達的空間位置坐標分別為：R1(80,0,0),R2(30,60,0),R3(55,110,0),R4(105,110,0),R5(130,60,0)(單位：km)。利用首點迭代法[9]產生1條虛假航跡如圖4所示,其中假目標初始位置坐標為(60 600 m,69 982 m,7 995 m)。假定無人機編隊數量為9架,取Δt=10 s,T=200 s,即組網雷達探測時間間隔為10 s,無人機飛行時間為200 s。2種算法初始參數具體設置如下。

圖4 預設假目標欺騙軌跡示意圖

粒子群優化算法求解的初始參數設置為：迭代次數N=100,種群數量M=50,欺騙航跡條數L=20,慣性權重ω=1.2,學習因子c1=c2=2。

改進粒子群優化算法求解的初始參數設置為：迭代次數N=100,種群數量M=50,欺騙航跡條數L=20,隨機慣性權重ωmin=0.6、ωmax=1.5,學習因子c1=c2=2,擾動因子c3=0.2。

4.2 仿真實驗結果

利用粒子群優化算法以及改進粒子群優化算法分別對多機協同欺騙干擾模型進行優化,仿真結果表明：在初始設定欺騙航跡條數L=20的條件下,利用9架無人機對組網雷達進行航跡欺騙干擾,2種算法優化的結果均能產生4條虛假航跡,2種算法優化產生的假目標航跡以及對應算法的適應度值收斂曲線見圖5～圖8。其中算法適應度收斂曲線橫坐標表示該算法優化時的迭代次數,縱坐標表示該算法優化求解模型過程中最多航跡欺騙條數的變化。

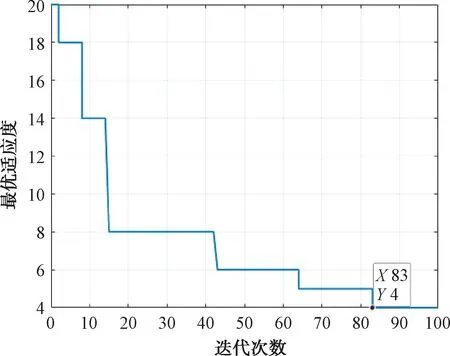
圖5 粒子群算法適應度值收斂曲線

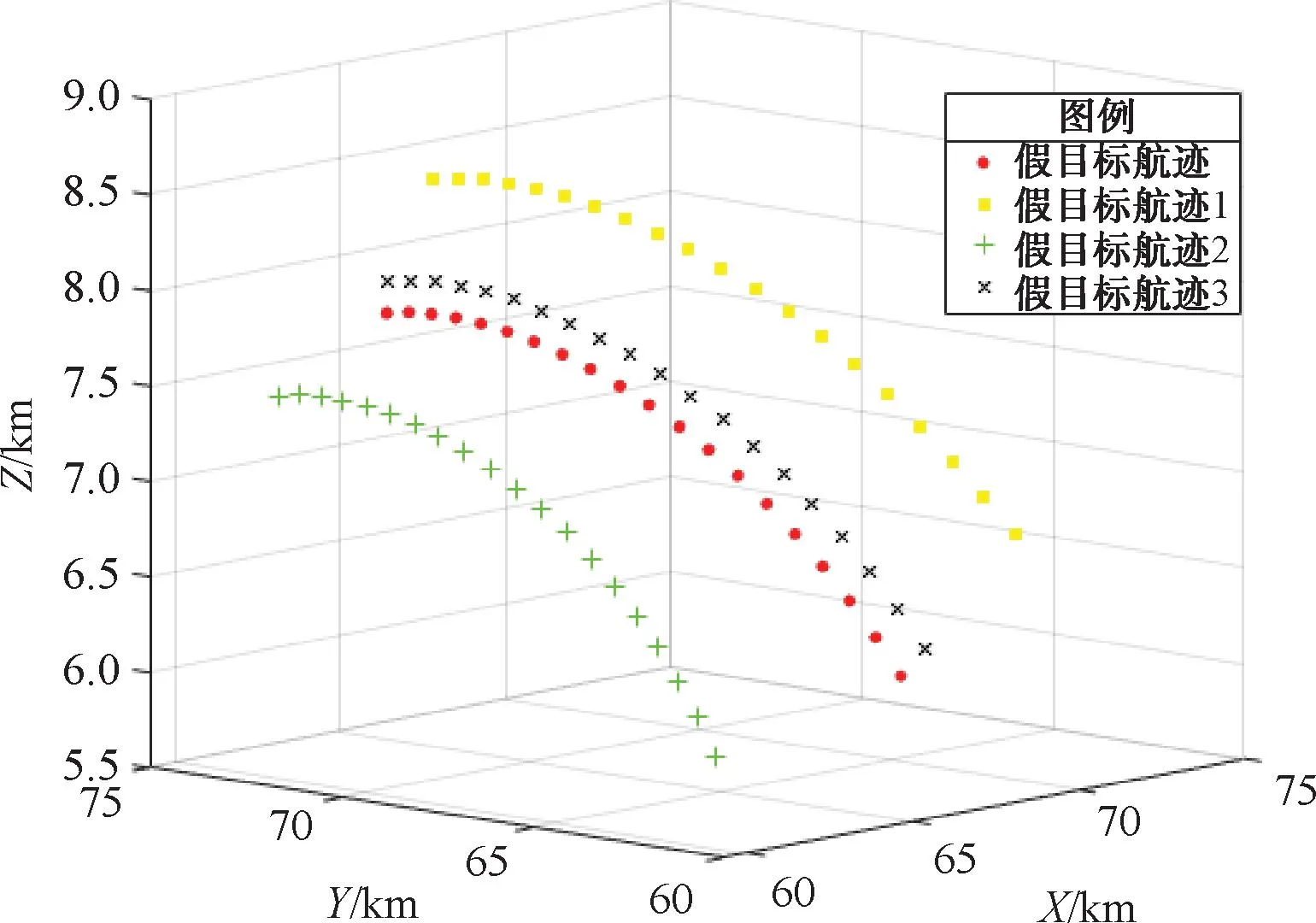
圖6 粒子群算法產生假目標航跡圖

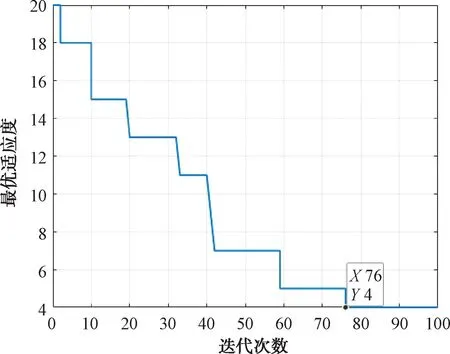
圖7 改進粒子群算法適應度值收斂曲線

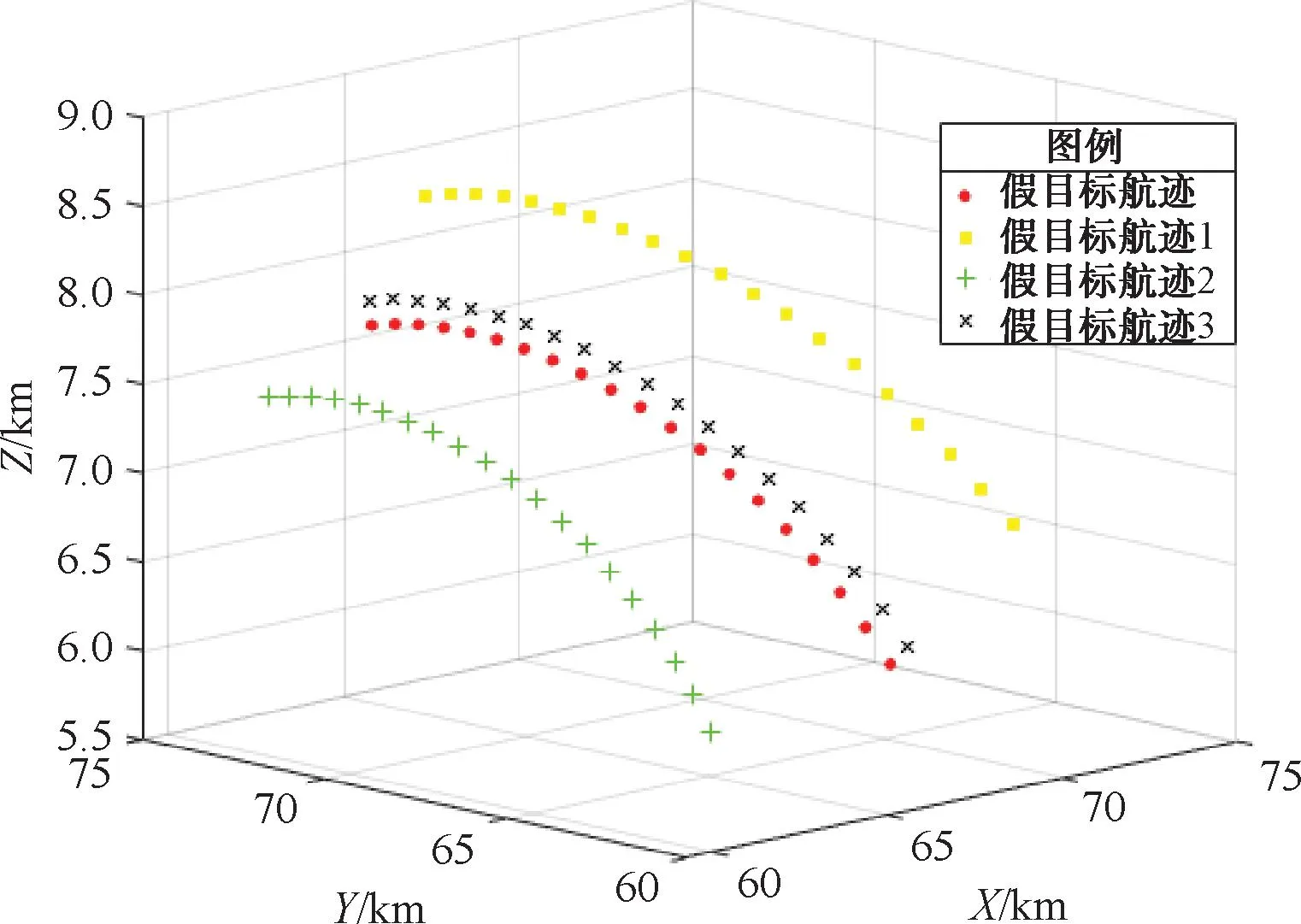
圖8 改進粒子群算法產生假目標航跡圖

4.3 算法分析與評價

(1) 算法效率

采用2種算法對多機協同欺騙干擾模型進行優化求解的平均執行時間以及最大迭代次數如表1所示。由此可以得出,2種算法效率為：IPSO>PSO。

表1 2種算法運行效率對比

(2) 算法全局尋優能力

改變無人機編隊的數量,利用2種算法求解在不同無人機架數的條件下各自算法的最優適應度值,結果如圖9所示。由此可知：改進后的粒子群算法在處理大規模優化問題時,不容易陷入局部最優,能表現出較好的全局搜索能力。

圖9 2種算法在不同無人機數量下的最優適應度值

5 結束語

多無人機協同航跡欺騙干擾組網雷達系統需要考慮組網雷達系統“同源檢測”規則,屬于大規模優化問題,通常需要采用群體智能算法對無人機的飛行任務進行優化。針對標準粒子群優化算法對該類問題求解時存在算法效率低、容易陷入局部最優等問題,本文提出了一種基于改進粒子群優化算法的多無人機協同干擾技術,通過仿真實驗驗證了改進粒子群優化算法相較于標準粒子群優化算法具備更快的收斂速度和全局尋優能力,對于利用無人機對組網雷達進行協同干擾具有一定的參考價值。