基于改進GM(1,1)模型的生活用水量預測

高華昆, 陶月贊, 楊 杰

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

隨著城市化的發展和居民生活水平的提高,生活用水量持續增加,生活用水供需矛盾日益突出[1]。因此精準合理地預測生活用水量,有助于緩解用水供需矛盾,也是水資源保護、管理的研究熱點。生活用水量從較長時間看,具有逐年增長的趨勢,為其預測奠定了基礎。常用的用水量預測方法有城市綜合指標法、系統動力學法、灰色預測模型法等[2-4]。

灰色系統理論認為任何隨機過程都可以看成一定時空區域內變化的灰色過程,灰色系統即部分信息已知、部分信息未知的系統,該理論是文獻[5]提出的,灰色預測模型是灰色系統理論的一部分。對于生活用水量的預測,已知信息為用水量,但是影響用水量的其他因素難以明確得知,即為未知信息,如氣候、行政管理措施、人口規模等,因此可將其視為灰色系統,灰色預測模型是適用的[6]。該模型廣泛應用于人口預測、經濟預測、電力預測等[7-9]。自GM(1,1)模型提出至今,國內外學者不斷對其進行改進,文獻[10]基于新信息優先原理提出非等間距GM(1,1)優化模型,改進后的模型能夠充分利用信息,從而提高預測精度;文獻[11]利用拉格朗日中值定理將背景值構造為與初始值相關的變量,有效提高模型的預測精度;文獻[12]分析非等間距GM(1,1)模型中的背景值,提出用Newton插值和數值積分中的Newton-Cores、Gauss-Legendre公式分別重構模型中的背景值,數據模擬結果充分說明新模型的有效性和優越性;文獻[13]通過對非等間距原始序列背景值進行改進,拓寬GM(1,1)模型的適用范圍和精準度。

國內外學者大多引入積分差值、向量等方法改進GM(1,1)模型,這些方法雖然取得不錯的預測效果,但是較為煩瑣,不利于預測結果的計算。通過對GM(1,1)模型的研究,發現灰色預測模型的誤差來源主要是初始條件和背景值[14-15]。本文在上述研究的基礎上引入冪函數優化背景值、原始序列進而改進GM(1,1)模型,并將其應用于河南省生活用水量預測中,以期能用少量的數據進行中長期用水量預測,為城市供水管理、水資源持續利用提供幫助。

1 GM(1,1)模型的改進

1.1 GM(1,1)模型及其局限分析

經典GM(1,1)模型的構造如下,原始序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}為非負序列,經累加得到:

x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}

(1)

對序列x(1)(k)的緊鄰數據求均值,生成z(1)(k)序列,即

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(2)

構造矩陣B與矩陣Y,采用最小二乘法求參數a、b,即

Y=[x0(1)x0(1) …x0(n)]T,

[ab]T=(BTB)-1BTY

(3)

其中:a為發展系數;b為灰色作用量。

GM(1,1)模型的時間響應函數為:

(4)

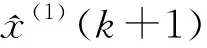
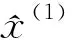
(5)

按照式(1)～(5) 構造的模型即為經典GM(1,1)模型。

通過上述建模分析,可以發現經典GM(1,1)模型存在如下缺點:

1) GM(1,1)模型的擬合和預測精度與a、b值有關,a、b的計算數值依賴于原始序列和背景值,因此式(2)的構造是造成擬合誤差的因素之一。

1.2 GM(1,1)改進模型

經典GM(1,1)模型在構造緊鄰均值序列z(1)(k)時,所使用的方法為式(2)。此方法使得x(1)(k)中的每個數據均處于同等地位,導致新數據比舊數據沒有優勢,從而影響預測精度。為了削弱此種影響,使新數據占主導地位,文獻[12]運用Newton-Cores、Gauss-Legendre公式進行改進背景值,此方法較為煩瑣,不利于計算。本文構造新的序列Z(1)(k),即

(6)

式(6)對原有序列式(2)進行改進,新序列可抽象為冪函數。當N取2時,Z(1)(k)與z(1)(k)兩序列相同。

按式(1)、式(6)、式(3)～(5) 順序重新構造GM(1,1)模型,即優化背景值進而改進GM(1,1)模型,為便于比較,本文將此種構造方法記為模型Ⅱ。

經典GM(1,1)模型在使用過程中需要原始數據離散且非負,通過一次累加生成削弱隨機性、有規律的離散序列。為增大此種影響,使原始序列隨機性減小、規律性增大,更能適合GM(1,1)模型。文獻[16]引入緩沖算子對原始序列進行改進,緩沖算子雖然能有效減小預測產生的誤差,但是需要滿足不動點公理、信息充分利用公理、解析化和規范化公理方可使用。同時,當原始序列為振蕩序列時,預測效果不如單調增長序列或單調衰減序列,而實際工程中很多原始數據是振蕩序列。因此本文在前人研究的基礎上進行總結,采用新的序列X(0)(k)代替原始序列x(0)(k)進行模型優化改進,新序列也可抽象為冪函數表示,即

(7)

按式(1)、式(7)、式(2)～(5) 順序重新構造GM(1,1)模型,即優化原始序列進而改進GM(1,1)模型,本文將此種構造方法記為模型Ⅲ。

1.3 模型檢驗

對灰色預測模型及其相關改進模型的檢驗方法較多,常用的預測性能檢驗方法主要有均方誤差、均方根誤差、標準誤差、平均相對誤差等[6]。幾種檢驗方法相似,為了運算簡便,本文選取平均相對誤差法進行預測性能檢驗。常用的預測精度檢驗方法主要有殘差檢驗、灰色關聯度檢驗、后驗差檢驗[17]。殘差檢驗僅對殘差序列進行檢驗從而得出模型的預測性能,檢驗序列較少,因此本文采用灰色關聯度檢驗和后驗差檢驗。

令εi為原始數據與預測數據的殘差,即

在錨桿支護應力場試驗臺上安裝1根錨桿，對比分析金屬托盤和金屬托盤+木墊板2種情況下錨桿預緊力損失、轉矩轉化、支護預應力場分布。錨桿采用現場采取的長度2 400 mm、直徑22 mm的左旋無縱肋螺紋鋼錨桿。錨固方式為加長錨固，錨固長度1 200 mm。為了更好地模擬井下實際工作狀態，使用井下常用的金屬網作為護表構件，安裝結果如圖3所示。

1) 平均相對誤差。平均相對誤差檢驗是對模型預測和仿真性能的檢驗,可以有效地反映出預測模型的真實值與預測值之間的差異[18],即

(8)

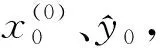
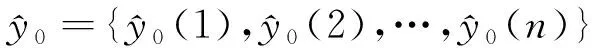
(9)

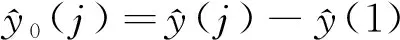
(10)

其中:i=1,2,…,n;j=1,2,…,n。

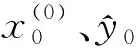
(11)

其中

3) 后驗差檢驗。后驗差檢驗主要由均方差比C、小誤差概率P2個檢驗組成,該方法以殘差序列為研究對象,檢驗殘差的概率分布[21]。

(12)

(13)

(14)

(15)

平均相對誤差檢驗是模型預測精度方面的檢驗方法,絕對關聯度檢驗、后驗差檢驗是模型擬合精度方面的檢驗。相對誤差越小,模型預測精度越高;C越小,模型預測精度越高,表明原始數據很離散,而模型計算值與實際值之間并不太離散;P和C同時進行精度刻畫,P越大,精度越高,表示殘差與殘差平均值之差小于給定值0.674 5S1的點較多[22]。通過檢驗可將模型劃分為4個等級,模型精度等級參數取值見表1所列[23]。

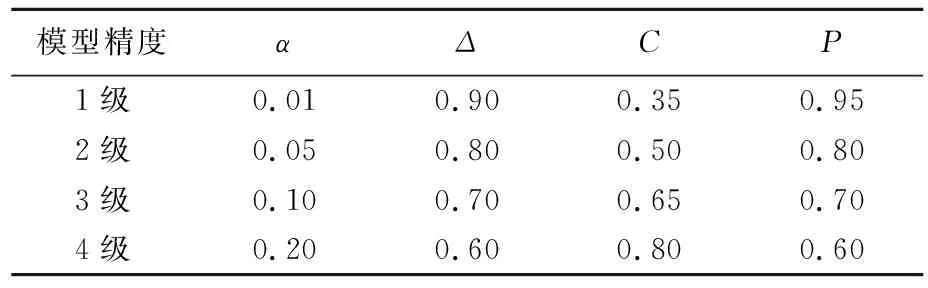
表1 模型精度等級參數取值

2 實例分析

2.1 數據來源

為了便于與其他改進方法進行比較,本文采用文獻[24]提供的河南省2012—2018年生活用水量數據及改進模型(記為模型Ⅰ)進行橫向對比,結果見表2所列。通過查閱《河南省水資源公報》,利用2019—2020年實際用水量數據作為預測檢驗。模型Ⅰ與文獻[10]所提出的改進模型相似,改進背景值計算方法進而改進GM(1,1)模型。

表2 河南省2012-2018年居民生活用水量 單位:108m3

2.2 模型構建

對表2中的數據分別使用經典GM(1,1)模型、模型Ⅰ、模型Ⅱ、模型Ⅲ建模,對生活用水量進行模擬預測。模型Ⅱ、模型Ⅲ構建時,N與M的選擇至關重要,經過多次重復試驗,N取3、M取2時,效果最好。

經典GM(1,1)模型為:

(16)

模型Ⅰ為:

(17)

模型Ⅱ為:

(18)

模型Ⅲ為:

(19)

通過式 (16)～(19) 求出4種模型的模擬預測值和誤差結果,見表3所列。

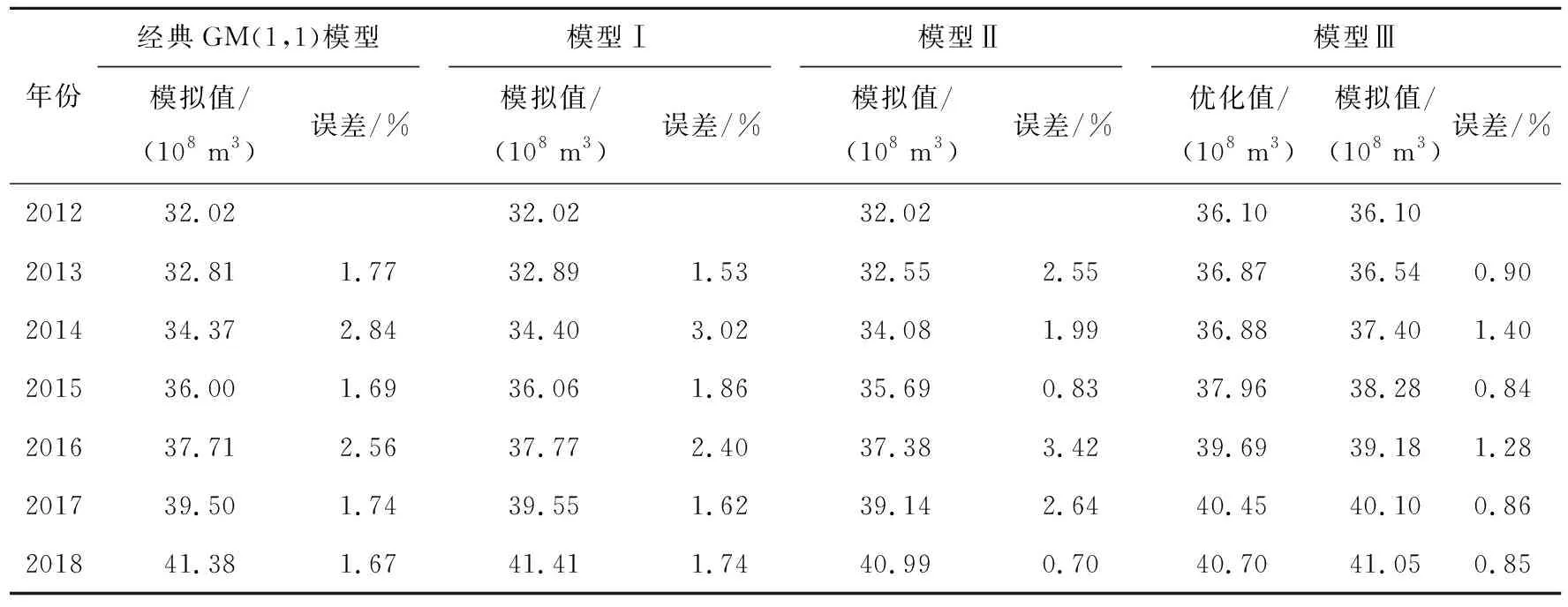
表3 2012-2018年4種模型用水量模擬結果對比

由上述分析及表3可知:模型Ⅰ、模型Ⅱ同為優化背景值進而改進GM(1,1)模型,但模型Ⅰ出現的最大誤差年份為2014年,誤差為3.02%;模型Ⅱ出現的最大誤差年份為2016年,誤差為3.42%;GM(1,1)模型的最大誤差年份為2014年,誤差為2.84%。對比模型Ⅰ、模型Ⅱ發現使用積分的方法改進背景值優于引用冪函數的方法改進背景值,但兩者改進后的模型均出現了最大誤差大于GM(1,1)模型。模型Ⅲ對比GM(1,1)模型,則最大誤差大幅減小。模型Ⅲ出現最大誤差的年份也是2014年,但僅為1.40%。

經典GM(1,1)模型、模型Ⅰ、模型Ⅲ產生最大誤差的年份為2014年,通過2014年實際用水量以及預測用水量發現4種模型的預測值均大于實際值。此種現象普遍存在于GM(1,1)模型在進行等間距預測時,原始數據變化差異較大,從而造成預測誤差變大。模型Ⅲ雖進行了優化原始序列,減少此類誤差產生,但無法消除。

2.3 模型檢驗

采用式(8)～(15)檢驗4種模型的模擬預測效果,結果見表4所列。

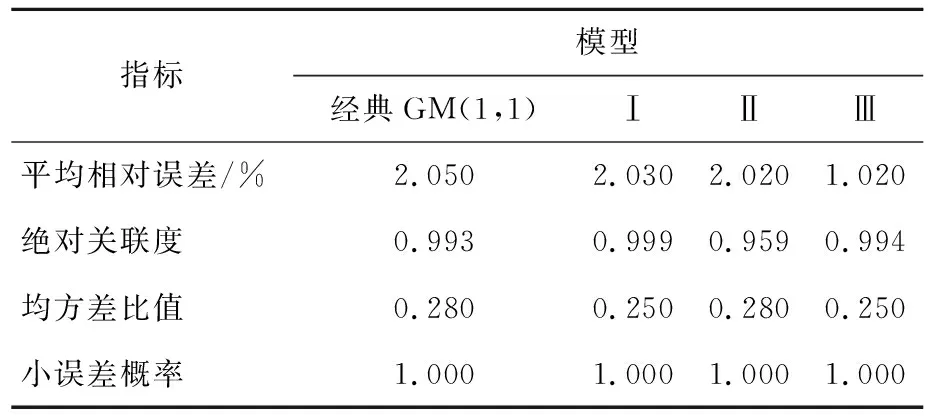
表4 4種模型的精度檢驗

由表4可知,4種模型在絕對關聯度、均方差比值和小誤差概率檢驗相差不大,絕對關聯度大于0.900,均方差比值小于0.350,小誤差概率大于0.950。在不計入平均相對誤差指標分析時,4種模型的精準度為一級精度模型。通過平均相對誤差檢驗可以發現,模型Ⅲ的平均相對誤差最小,經典GM(1,1)模型、模型Ⅰ、模型Ⅱ產生的平均相對誤差基本相同,約為模型Ⅲ平均相對誤差的2倍。

本文所采用的2種改進方法在模型擬合精度方面沒有顯著提高,但模型Ⅲ在預測精度上有顯著提高,模型Ⅱ卻無明顯變化。這表明模型Ⅲ更具優越性,具有較好的工程應用價值。

2.4 用水量預測

通過上述分析可知模型Ⅲ更具預測的優越性,但上述4種模型在精度等級上都可以進行中長期用水量預測。

為了檢驗模型Ⅲ是否更適合河南省生活用水量預測,本文根據上述4種模型,通過式(13)～(16)預測2019—2020年用水量,結果見表5所列。

表5 2019—2020年4種模型用水量誤差對比

雖然4種模型都適用于河南省生活用水量預測,但由表5可知,模型Ⅲ進行河南省生活用水量預測時效果最好。4種模型的平均相對誤差分別為4.76%、4.91%、3.70%、0.63%,模型Ⅲ2019年、2020年的誤差分別為0.99%、0.27%,預測精度遠超前3種模型,更適合進行河南省生活用水量預測。模型Ⅲ的預測結果較為理想,但在實際問題使用時會受到其他因素的影響,如引江濟淮工程、《地下水管理條例》施行等,造成供水水源、水量發生變化。這些變化在一定程度上會影響預測結果的精準度,因此在作出預測前要求用水過程不會發生結構性變化。

綜上所述,使用模型Ⅲ進行河南省生活用水量預測,預測出2021—2025年用水量分別為44.02×108、45.05×108、46.11×108、47.20×108、48.31×108m3。

3 結 論

1) 對4種模型進行比較,可知模型Ⅰ、模型Ⅱ在理論上屬于構造新的緊鄰均值序列,兩者模擬結果及相應預測的誤差相近,較GM(1,1) 模型精度略有提高;模型Ⅲ屬于優化原始值改進GM(1,1)模型,其預測精度明顯高于前3種改進模型。引入冪函數優化原始值比優化背景值更能提高GM(1,1)模型的預測精度。

2) 模型Ⅲ對河南省生活用水量進行中長期預測,預測效果在4種模型中相對最優。在滿足用水過程中不發生結構性變化時,預測2025年用水量為48.31×108m3。但在實際用水過程發生變化時,使預測結果精準度進一步提高是下一階段研究的重點。