中空注漿錨桿在淺埋暗挖法隧道中的應用與參數優化研究
摘要 文章以淺埋暗挖法隧道施工過程中最為典型的注漿錨桿為研究對象,通過理論分析,對中空注漿錨桿長度L和注漿半徑r提出了優化建議,結合工程實例進行數值模擬,對設計過程中的錨桿支護參數提出合理化建議。研究結果表明:(1)圍巖錨固體軸力與剪切應力與錨固體初始軸向力呈正相關,在錨固體力學參數一定的情況下,錨桿長度L直接影響錨固體軸向荷載,而注漿半徑r與剪切應力成反比關系。(2)增加錨桿長度能夠增加錨桿的錨固力作用,但隨長度的增加,其提升效果在錨桿長度超過3 m之后并不明顯;注漿半徑r>0.5 m后,剪應力峰值繼續減小,但降低幅度在5%以內。(3)數值模擬結果與理論分析結果具有一致性,L>3 m的部分,錨桿軸力已下降至30 kN以下,工程中考慮適當強度的安全儲備L可取3.5 m。研究結果能夠降低施工過程對深層圍巖的擾動,也提高經濟效益,可為淺埋暗挖法中空注漿錨桿支護設計參數提供一定的借鑒與參考。
關鍵詞 中空注漿錨桿;參數優化;數值模擬;隧道工程
中圖分類號 U452.2+5 文獻標識碼 A 文章編號 2096-8949(2024)04-0074-04
0 引言
錨桿支護在隧道開挖過程中,具有控制圍巖變形的作用,相較于普通砂漿錨桿,中空注漿錨桿憑借其特有的錨固機制,大幅度提高了錨桿的錨固性能[1-2]。劉貝、周東對中空注漿錨桿進行了參數化建模分析,結合工程案例優化了新奧法和淺埋暗挖隧道的參數化建模方法[3];余建雨、楊健輝從受力機理、錨護結構方面對比了普通砂漿錨桿與中空注漿錨桿的差異,數值模擬結果顯示:中空注漿錨桿錨固性能優于普通砂漿錨桿[4];劉江、王軍等以工程實際為背景,對比分析了中空注漿錨桿和普通砂漿錨桿加固原理,通過注漿試驗確定了最佳注漿比例,為實際工程提供了初期支護優化的設計理念[5];蔡俊華、盧偉平等研究了注漿水泥齡期對中空注漿錨桿的動力檢測效果的影響,結合現場試驗和數值模擬,給出了中空注漿錨桿最佳動力檢測時間[6]。以上研究重點集中在對中空注漿錨桿加固原理和自身加固性能上,少有結合隧道施工工法對支護體系設計參數提出優化設計,該文特以淺埋暗挖法隧道施工過程中最為典型的注漿錨桿為研究對象,結合理論分析與數值模擬,對設計過程中的錨桿支護參數提出合理化建議,并應用于工程實踐。
1 理論分析
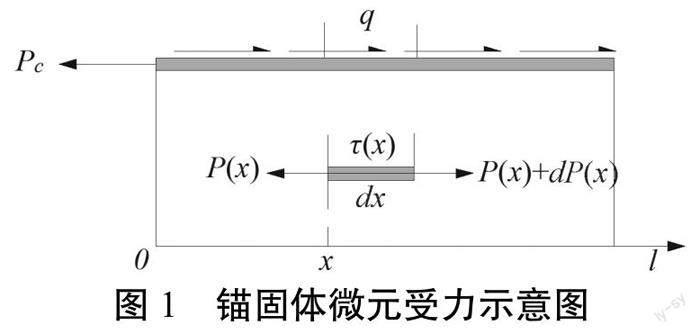
如圖1所示,為錨固體微元體基本受力模型,圖中,Pc為錨固體初始段承受的軸向荷載(kN);P(x)為錨固體任意一點的軸向荷載(kN);q為微元體表面應力(kN/mm);τ(x)為錨固體剪切應力(kN/mm)。根據局部變形理論,錨固體與危巖體表面的剪應力關系可表示為:
式中,r——錨固體半徑,以上解析式可以看出,圍巖錨固體軸力與剪切應力與錨固體初始軸向力呈正相關,且錨固體自身力學參數ks、Ea、Aa直接影響軸向荷載和剪應力的大小。
2 中空注漿錨桿參數優化設計
特以萬州區北濱大道拓寬改造工程為例。匝道A線隧道,位于北濱大道與外貿路交叉口處,隧道起止里程為匝道A線K0+078~K0+203,全長125 m,單洞單線隧道,錨桿擬采用中空注漿錨桿。實測得圍巖剪切模量k1=12.8 MPa,外側注漿體剪切模量k2=16.2 MPa,錨桿剪切模量k3=16.2 MPa,錨固體等效彈性模量為21.5 MPa。
2.1 錨桿長度優化分析
分別取L=1 m、2 m、3 m、4 m、5 m,錨固體半徑r=0.5 m,通過計算獲得ks=7.37 MPa,α=0.721,繪制錨固體軸向荷載與剪應力分布曲線如圖2、圖3所示。
如圖2所示,初始拉拔力控制在200 kN,沿錨固體軸向長度方向,軸向荷載呈現遞減趨勢,尤其在1 m長的中空注漿錨桿中,軸向荷載呈直線遞減,斜率為定值,錨桿長度增大過程中,軸向荷載曲線逐漸呈現雙曲線形分布,具體體現在曲線斜率逐漸減小,2 m長的中空注漿錨桿,軸向荷載傳遞至1 m處時,僅剩62 kN,軸向荷載損失率為69%。3 m長的中空注漿錨桿,荷載傳遞至2 m處時,僅剩25 kN,錨桿繼續深入巖層時,軸向荷載幾乎趨于0。圖中可以看出,4 m和5 m長的中空注漿錨桿軸向荷載分布曲線,與3 m錨桿軸向荷載曲線差異不大,深入巖層3 m以后軸力在遠端幾乎不再分布。
在圖3中,錨固體剪切應力隨錨桿長度的增加而減小,分布形式大致相同,而1 m長的錨桿應力分布區間為60~80 MPa,與其他錨桿應力分布區間差異較大,2 m長中空注漿錨桿剪應力峰值為51 MPa,至錨桿末端仍存在20.5 MPa的剪切應力,3~5 m長中空注漿錨桿剪切應力越往末端其變化值越小,剪切應力曲線斜率趨近于0,應力趨于平緩,分別為10.2 MPa、9.5 MPa和8.9 MPa,增加錨桿長度能夠增加錨桿的錨固力作用,但隨長度的增加,其提升效果在錨桿長度超過3 m之后并不明顯,錨桿長度超過4 m后,端部幾乎不再提供錨固力,工程中建議將中空注漿錨桿長度控制在3~3.5 m范圍以內。
2.2 注漿圈半徑優化分析
根據公式(6)可知錨固體半徑r僅與剪應力分布呈負相關,結合前文研究結果,取L=3 m,錨固半徑分別取r=0.1 m、0.3 m、0.5 m、0.7 m、0.9 m,繪制剪應力分布曲線如圖4所示。
圖4中:錨固半徑r=0.1 m,由于注漿半徑較小,錨桿周圍巖體較為破碎,中空注漿錨桿的注漿優勢尚未充分發揮,剪切應力最大值為223.5 MPa,此條件下錨固性能不佳,注漿半徑增大至0.3 m時,峰值剪應力減小至74.65 MPa,降幅達66.6%,此時中空注漿錨桿充分發揮注漿優勢,周圍破碎巖在注漿液擴散過程中逐漸形成一個整體,剪切模量ks提高,錨固性能得到充分利用,應力峰值降低明顯;注漿半徑r=0.5 m,剪應力峰值繼續降低至45.38 MPa,降低幅度為39.2%,繼續增大注漿半徑,剪應力峰值繼續減小,但降低幅度有限;當注漿半徑r=0.7 m時,剪應力峰值為43.29 MPa,r=0.9 m時,剪應力峰值為42.38 MPa,降低幅度在5%以內,剪應力分布曲線趨于平緩,此時可認為中空注漿錨桿注漿優勢已充分發揮,繼續擴大注漿范圍不再具有工程實際意義,單根中空注漿錨桿注漿半徑宜控制在0.5 m左右。
3 工程應用
3.1 工程概況
匝道A線隧道為工程背景,該隧道起訖樁號為K0+078~K0+203,全長125 m,單洞單線隧道,隧道埋深8.35~17.85 m,建筑限界10.75 m,限界凈高5.0 m,圍巖等級分別為Ⅳ級圍巖(38.9%)和Ⅴ級圍巖(61.1%)。
3.2 支護方案
隧道洞身按新奧法原理進行設計,初期支護采用濕噴射混凝土、錨桿、鋼筋網加型鋼鋼架或鋼格柵拱架支護組合使用,錨桿擬采用中空注漿錨桿;二次襯砌采用整體式模筑C35防水鋼筋混凝土結構,兩層支護間設置柔性防水層,襯砌支護參數如表1所示。
3.3 數值模擬
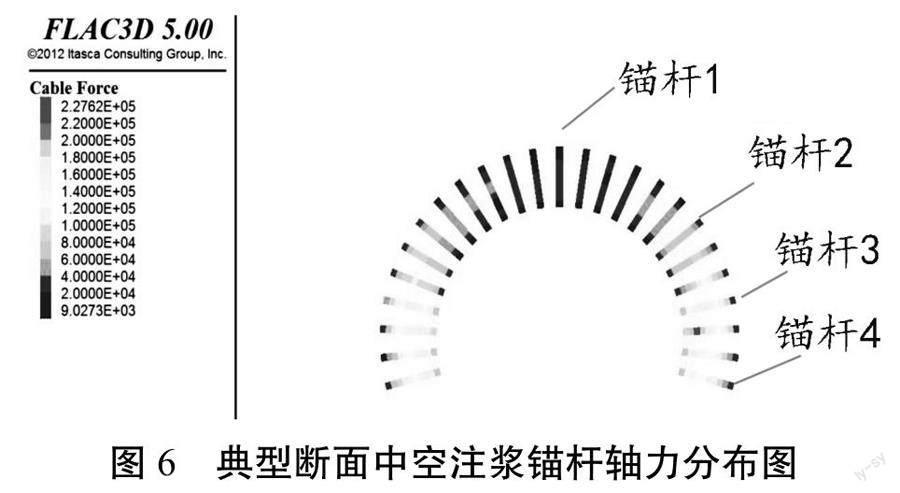
特選取Ⅴ級圍巖區段隧道襯砌支護中的中空注漿錨桿為數值模擬對象,探究該區段錨桿位移和受力特點,以FLAC3D為數值模擬工具,建立數值模擬模型如圖6所示,模擬開挖工況與實際隧道開挖工況保持一致,注漿半徑r為0.5 m,中空注漿錨桿支護參數如表2所示。
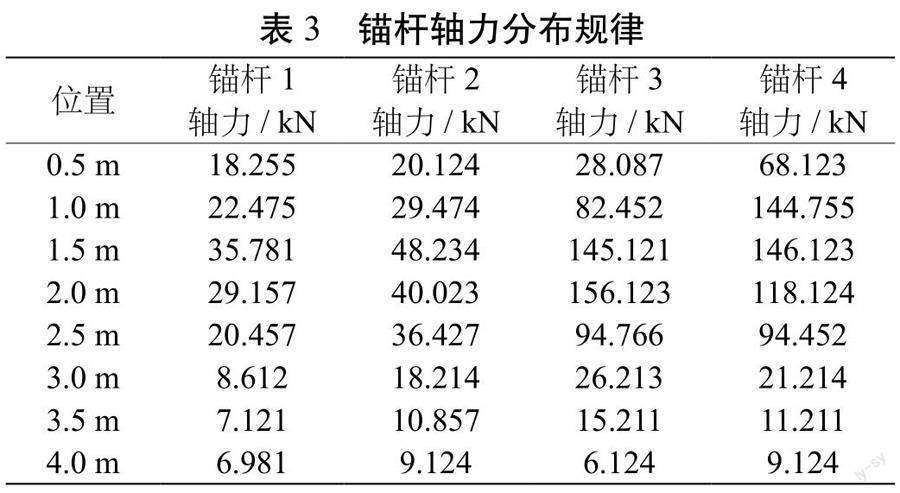
進洞后,隧道中部斷面中空注漿錨桿位移如圖5所示,同一截面處,錨桿軸力分布如圖6所示。取典型部位錨桿編號錨桿1~4,利用FLAC3D數據提取功能,測取對應錨桿軸力分布情況,統計表如表3所示。
數值模擬結果顯示:Ⅴ級圍巖區段,采用上述支護方式的中空注漿錨桿位移最大值位于兩端拱腳處,最大值為0.71 mm,錨桿位移沿拱圈向拱頂遞減,拱頂位置位移最小為0.06 mm,圖6中,不同位置的錨桿,其軸力分布均勻性不一,拱頂位置的錨桿1整體軸力較小且均衡,最大值出現在1.5 m處為35.781 kN,隨后逐漸減小,深入巖層3 m之后,錨桿軸力降低至10 kN以下,且后續壓力分布變化較小,表明在拱頂位置的中空注漿錨桿未能充分發揮其錨固作用,此部分錨桿具有較高的安全貯備;拱肩上部錨桿2軸力峰值也出現在1.5 m處,較拱頂最大峰值增加了12.453 kN,各對應位置也較拱頂錨桿軸力增加了約25%,拱肩下部錨桿3軸力沿錨桿長度方向出現了明顯的先增大,后減小的分布規律,最大峰值出現在2 m處為156.123 kN,拱腳錨桿4軸力分布同錨桿3一致,但峰值僅為146.123 kN,較錨桿3峰值降低了6.4%。
錨桿軸力沿軸向的分布規律與理論分析的結果不一致,實際工程中,沿錨桿長度方向錨桿軸力先增大后減小,峰值出現在0.375L~0.5L處,且錨固末端(x=L)也存在一定程度的軸向力,此結論與公式(6)理論計算結果存在一定差異,原因在于實際工程中,錨桿位移較小時(如錨桿1和錨桿2),支護能力沒有得到充分發揮,初期支護中鋼筋網和噴射混凝土在較大程度上分擔了外部荷載的作用,而分擔的比例沿錨桿長度方向遞減,因此錨桿峰值會出現在0.375L~0.5L處,另外理論分析中對邊界條件進行了理想化處理,工程中地質條件復雜,錨桿末端受力與工程地質有較大關系。
該工程中,圍巖等級Ⅴ級區段中空注漿錨桿長度L=4 m,根據該文理論計算結果,錨桿長度在超過3 m后,其錨固性能基本不再有明顯的提升作用。對實際工程的數值模擬結果也可看出,L>3 m的部分,錨桿軸力已下降至30 kN以下,錨桿末端的錨固性能并不能得到充分的利用。因此,在工程設計中,可結合數值模擬結果,對工程設計參數提出適當優化措施,該工程錨桿長度可優化至L=3 m,考慮適當強度的安全儲備,L可取3.5 m,優化結果能提高經濟效益,也降低了施工過程對深層圍巖的擾動。
4 結論
圍巖錨固體軸力與剪切應力與錨固體初始軸向力呈正相關,且錨固體自身力學參數ks、Ea、Aa直接影響軸向荷載和剪應力的大小,在錨固體力學參數一定的情況下,錨桿長度L直接影響錨固體軸向荷載,而注漿半徑r與剪切應力成反比關系。
增加錨桿長度能夠增加錨桿的錨固力作用,但隨長度的增加,其提升效果在錨桿長度超過3 m之后并不明顯;注漿半徑r >0.5 m后,剪應力峰值繼續減小,但降低幅度在5%以內。理論結果顯示,對于破碎圍巖中的中空注漿錨桿長度宜控制在3~3.5 m,注漿半徑不超過0.5 m。
匝道A線隧道數值模擬結果與理論分析結果具有一致性,L>3 m的部分,錨桿軸力已下降至30 kN以下,錨桿末端的錨固性能并不能得到充分的利用,工程中考慮適當強度的安全儲備,L可取3.5 m,優化結果能夠提高經濟效益,也降低了施工過程對深層圍巖的擾動。
參考文獻
[1]孫振宇, 張頂立, 房倩. 隧道錨固系統的協同作用及設計方法[J]. 工程力學, 2019(5):? 53-66+75.
[2]張頂立, 孫振宇, 侯艷娟. 隧道支護結構體系及其協同作用[J]. 力學學報, 2019(02):? 577-593.
[3]劉貝, 周東明. 基于Revit的隧道參數化建模研究[J]. 工程建設, 2019(9):? 23-28+47.
[4]余建雨, 楊健輝. 中空注漿錨桿與普通砂漿錨桿加固效果的比較[J]. 工業建筑, 2016(11):? 137-141.
[5]劉江, 王軍, 徐騰輝. 漲殼式預應力中空錨桿在機械化開挖大斷面隧道中的施工應用研究[J]. 隧道建設(中英文), 2018(S2):? 324-329.
[6]蔡俊華, 盧偉平, 閆小波. 中空注漿錨桿的動力響應特征及質量評價研究[J]. 施工技術(中英文), 2021(23):? 94-97+106.
收稿日期:2023-12-01
作者簡介:尹恒(1989—),男,碩士研究生,高級工程師,從事市政隧道、結構、巖土工程設計工作。

