一種GNSS/SINS組合導(dǎo)航的改進(jìn)魯棒濾波算法

孫玉梅，王學(xué)偉，任憲潔

(濰坊科技學(xué)院計(jì)算機(jī)學(xué)院，山東 濰坊 262700)

0 引言

目前,GNSS/SINS組合導(dǎo)航系統(tǒng)在航空、航天等諸多領(lǐng)域得到廣泛的應(yīng)用,通常使用卡爾曼濾波器(KF)作為其信息融合方法,然而KF只有在線性高斯?fàn)顟B(tài)空間模型及測(cè)量值服從高斯分布假設(shè)下才是最優(yōu)的[1]。然而在實(shí)際情況下,測(cè)量噪聲除了不服從高斯分布外,還容易受異常值的影響,導(dǎo)致KF濾波精度下降甚至發(fā)散[2]。為了處理非高斯噪聲,可以使用粒子濾波,然而粒子濾波應(yīng)用于組合導(dǎo)航系統(tǒng)時(shí)存在如下問(wèn)題[3]:計(jì)算量大,特別是組合導(dǎo)航系統(tǒng)是高維系統(tǒng);不能抵抗異常值的影響。而H∝濾波器能夠給出基于最小化最壞情形下的估計(jì)誤差,可有效解決測(cè)量噪聲中的不確定性,但也存在在測(cè)量異常值時(shí)發(fā)生濾波失效的缺陷[4]。

此外,魯棒濾波器可以有效處理非高斯分布及測(cè)量異常值的影響。其中,楊元喜院士對(duì)此開(kāi)展了早期的研究,并提出了諸多模型[5-7]。以此為基礎(chǔ),文獻(xiàn)[8-10]分別開(kāi)展了基于雙漸消因子及多重漸消因子的濾波算法研究,以消除濾波過(guò)程中的異常影響。文獻(xiàn)[11]基于模糊控制的隸屬函數(shù),設(shè)計(jì)了模糊強(qiáng)跟蹤擴(kuò)展卡爾曼濾波器,以補(bǔ)償GNSSS信號(hào)突變時(shí)對(duì)導(dǎo)航精度的影響,但該算法的精度嚴(yán)重依賴(lài)隸屬度函數(shù)。文獻(xiàn)[12]基于新息序列構(gòu)建了控制因子,并設(shè)計(jì)了一種魯棒濾波方法,以降低測(cè)量野值對(duì)濾波精度的影響。文獻(xiàn)[13]提出的基于三段權(quán)函數(shù)的組合導(dǎo)航系統(tǒng)抗差估計(jì)濾波方法。

1 GNSS/SINS組合導(dǎo)航系統(tǒng)模型

以松組合模式為例,建立GNSS/SINS組合導(dǎo)航系統(tǒng)的線性濾波模型[14]:

(1)

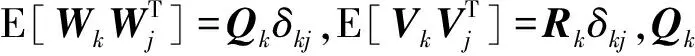
選取18維狀態(tài)向量:

(2)

測(cè)量向量Zk取為SINS和GNSS各自三維速度、三維位置之間的差值[14]。

農(nóng)村商業(yè)銀行對(duì)于我國(guó)農(nóng)村經(jīng)濟(jì)的發(fā)展至關(guān)重要，為解決農(nóng)商行發(fā)展中出現(xiàn)的股權(quán)結(jié)構(gòu)單一、股權(quán)高度分散、激勵(lì)機(jī)制缺失等諸多問(wèn)題，唯有對(duì)股權(quán)機(jī)制進(jìn)行創(chuàng)新，提出多元化的股權(quán)結(jié)構(gòu)，引入全周期監(jiān)管來(lái)預(yù)防系統(tǒng)性操作風(fēng)險(xiǎn)，充分維護(hù)中小股東的自身權(quán)益等，才可以保障農(nóng)商行在經(jīng)濟(jì)新常態(tài)的發(fā)展中穩(wěn)步前行。

2 改進(jìn)的魯棒濾波算法

2.1 問(wèn)題描述

(3)

(4)

(5)

Pk|k=(I-KkHk)Pk|k-1

(6)

(7)

(8)

(9)

式中:Zk|k-1為測(cè)量預(yù)測(cè)向量;Sk為其協(xié)方差矩陣。

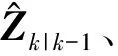
(10)

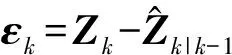
若測(cè)量向量不滿(mǎn)足高斯分布,即測(cè)量值存在異常值或測(cè)量噪聲不滿(mǎn)足高斯分布(該高斯分布被其他分布所污染)時(shí),則式(10)不再成立。此時(shí),可以通過(guò)假設(shè)檢驗(yàn)來(lái)檢測(cè)實(shí)際測(cè)量與假設(shè)模型的兼容性,具體做法如下:

取檢驗(yàn)統(tǒng)計(jì)量為[13]:

(11)

對(duì)于顯著性水平α,選取檢測(cè)閾值,且滿(mǎn)足:

P(γk≥χα)=α

(12)

式中P代表一個(gè)隨機(jī)事件發(fā)生的概率。當(dāng)γk<χα?xí)r,認(rèn)為測(cè)量正常;否則,測(cè)量異常。

嚴(yán)格意義上來(lái)說(shuō),GNSS輸出信息的統(tǒng)計(jì)特性并不服從于高斯分布,此時(shí)GNSS輸出信息的實(shí)際概率分布ρa(bǔ)ctual滿(mǎn)足[16]:

ρa(bǔ)ctual=(1-β)·ρnominal+β·ρperturbing

(13)

式中:ρnominal為標(biāo)準(zhǔn)的高斯分布概率密度函數(shù);β為污染分布的比值,且0≤β≤1;ρperturbing為干擾分布的概率密度函數(shù)。

當(dāng)測(cè)量向量不滿(mǎn)足高斯分布時(shí),傳統(tǒng)的方法是對(duì)測(cè)量噪聲協(xié)方差矩陣進(jìn)行加權(quán)或?qū)顟B(tài)一步預(yù)測(cè)協(xié)方差矩陣Pk|k-1進(jìn)行加權(quán),然而該加權(quán)對(duì)應(yīng)的權(quán)重值有可能過(guò)大或過(guò)小,進(jìn)而導(dǎo)致濾波誤差較大或?yàn)V波發(fā)散。

2.2 改進(jìn)算法的提出

為了解決上述問(wèn)題,基于牛頓迭代法提出了一種改進(jìn)的帶有比例因子的魯棒卡爾曼濾波器,具體思路表述如下:

(14)

基于調(diào)整后的測(cè)量噪聲協(xié)方差矩陣,下面的方程可以得到滿(mǎn)足:

(15)

式(15)可轉(zhuǎn)化為求λk的非線性問(wèn)題,即可通過(guò)式(16)計(jì)算式(14)中的λk:

(16)

針對(duì)式(16),利用式(17)的牛頓迭代法求解λk:

(17)

式中i為迭代次數(shù)。

由矩陣求導(dǎo)的原理,尤其是可逆矩陣的求導(dǎo)方法,不妨假設(shè)A是一個(gè)關(guān)于變量t的可逆矩陣,則:

(18)

結(jié)合式(16),把式(18)代入式(17),得:

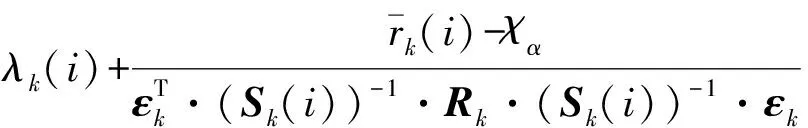
(19)

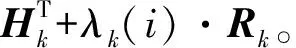
由式(19)完成比例因子的精確計(jì)算與選取。

經(jīng)過(guò)式(19)的迭代,最終得到了較精確的比例因子λk,進(jìn)而克服了文獻(xiàn)[8-12]中存在控制因子根據(jù)經(jīng)驗(yàn)設(shè)定而導(dǎo)致的組合導(dǎo)航濾波精度下降問(wèn)題。

綜上所述,文中提出的組合導(dǎo)航系統(tǒng)改進(jìn)魯棒濾波算法的流程圖如圖1所示。

圖1 改進(jìn)魯棒算法濾波流程圖Fig.1 Filter flowchart of improved robust algorithm

3 仿真結(jié)果及分析

3.1 仿真條件

為了驗(yàn)證上述算法的魯棒性及可靠性,對(duì)GNSS/SINS組合導(dǎo)航系統(tǒng)進(jìn)行仿真驗(yàn)證。飛行初始位置為(31°N,120°E,500 m),初始速度為0 m/s,初始航向?yàn)?0°,水平初始姿態(tài)角為0°;根據(jù)現(xiàn)有導(dǎo)航傳感器的實(shí)際精度,選取導(dǎo)航傳感器參數(shù)設(shè)置如表1所示。

表1 導(dǎo)航傳感器仿真參數(shù)設(shè)置Table 1 Simulation parameter setting of navigation sensors

設(shè)計(jì)了時(shí)長(zhǎng)為3 600 s的飛行軌跡,包含直線、變速、爬坡、轉(zhuǎn)彎、俯沖等機(jī)動(dòng)過(guò)程。

在仿真時(shí),β為0.2,ρperturbing為均值為0的中心卡方分布。同時(shí),在GNSS輸出信息的不同時(shí)刻上加入幅度不同的野值。

3.2 仿真結(jié)果及分析

基于上述仿真條件設(shè)定,采用常規(guī)卡爾曼濾波算法(KF)、傳統(tǒng)魯棒卡爾曼濾波算法[8-10,13](RKF)及文中所提出的改進(jìn)魯棒卡爾曼濾波算法(IRKF)的濾波結(jié)果進(jìn)行對(duì)比分析。

圖2～圖4給出了基于KF及IRKF的導(dǎo)航參數(shù)誤差對(duì)比曲線。圖5～圖7給出了基于RKF及IRKF的導(dǎo)航參數(shù)誤差對(duì)比曲線。通過(guò)對(duì)圖2～圖7的分析可以看出,基于IRKF的導(dǎo)航參數(shù)誤差更加平穩(wěn),而且對(duì)姿態(tài)角的濾波精度也較高、尤其是對(duì)航向角。

圖2 基于KF和IRKF的位置誤差曲線對(duì)比圖Fig.2 Position error curve comparison based on KF and IRKF

圖3 基于KF和IRKF的速度誤差曲線對(duì)比圖Fig.3 Velocity error curve comparison based on KF and IRKF

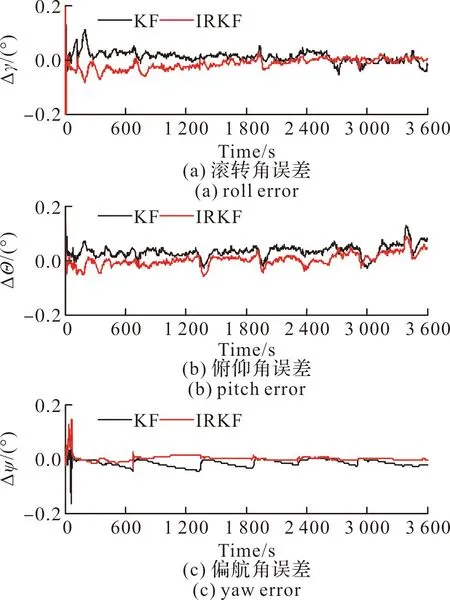
圖4 基于KF和IRKF的姿態(tài)誤差曲線對(duì)比圖Fig.4 Attitude error curve comparison based on KF and IRKF

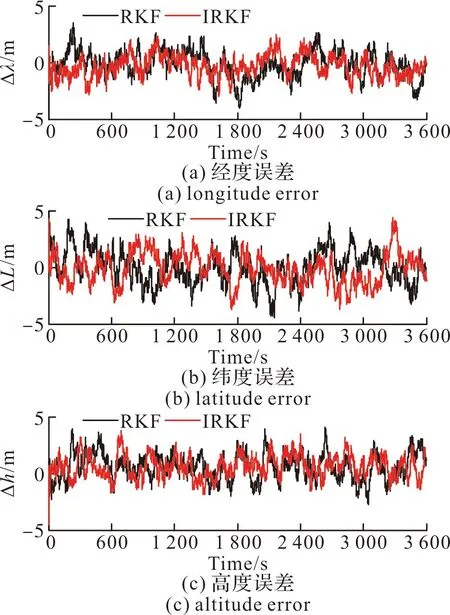
圖5 基于RKF和IRKF的位置誤差曲線對(duì)比圖Fig.5 Position error curve comparison based on RKF and IRKF

圖6 基于RKF和IRKF的速度誤差曲線對(duì)比圖Fig.6 Velocity error curve comparison based on RKF and IRKF

圖7 基于RKF和IRKF的姿態(tài)誤差曲線對(duì)比圖Fig.7 Altitude error curve comparison based on RKF and IRKF

為了更直觀分析圖2～圖7的結(jié)果,表2給出了各個(gè)導(dǎo)航參數(shù)對(duì)應(yīng)的均方根誤差(RMSE)。由表2可以看出,相對(duì)于KF,IRKF可提高位置及速度精度分別為14.1%及13.8%;相對(duì)于RKF,IRKF可提高位置及速度精度分別為8.1%及7.7%。

表2 基于KF、RKF及IRKF的各導(dǎo)航參數(shù)RMSETable 2 Navigation parameters RMSE based on KF,RKF and IRKF

出現(xiàn)上述結(jié)果的原因,可以通過(guò)基于KF、基于RKF及基于IRKF的故障檢測(cè)值曲線進(jìn)行解釋,其中基于KF的故障檢測(cè)值曲線如圖8所示。

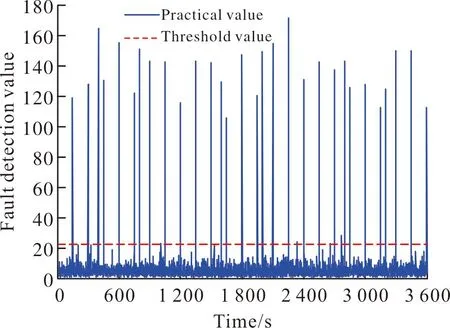
圖8 基于KF的故障檢測(cè)值曲線Fig.8 Fault detection value curve based on KF

由于測(cè)量值不滿(mǎn)足高斯分布、以及在導(dǎo)航過(guò)程的不同時(shí)刻測(cè)量值出現(xiàn)了不同幅度的野值,因此基于KF的故障檢測(cè)值在多個(gè)時(shí)刻超越檢測(cè)閾值,進(jìn)而引起濾波精度下降。基于RKF的故障檢測(cè)值曲線與圖8類(lèi)同,當(dāng)檢測(cè)到故障檢測(cè)值大于檢測(cè)閾值時(shí),RKF實(shí)時(shí)對(duì)測(cè)量噪聲方差矩陣進(jìn)行調(diào)整,進(jìn)而在一定程度上提高了濾波精度。但是該調(diào)整只是簡(jiǎn)單的、粗略的、且是基于人工經(jīng)驗(yàn)而設(shè)置的,因此基于RKF的導(dǎo)航濾波精度的提升是有局限性的。

基于圖1及式(18),IRKF的濾波過(guò)程引入了迭代過(guò)程,目的在于對(duì)測(cè)量噪聲方差矩陣的調(diào)整盡量達(dá)到最優(yōu)化。當(dāng)IRKF檢測(cè)到故障檢測(cè)值大于檢測(cè)閾值時(shí),其第一次迭代過(guò)程對(duì)應(yīng)的故障檢測(cè)值曲線也與圖8類(lèi)同,經(jīng)過(guò)多次迭代且不斷優(yōu)化測(cè)量噪聲協(xié)方差矩陣后,基于IRKF的故障檢測(cè)值曲線如圖9所示,所需要的迭代次數(shù)如圖10所示。

圖9 基于IRKF的故障檢測(cè)值曲線Fig.9 Fault detection value curve based on IRKF

從圖10可以看出,雖然IRKF在多數(shù)時(shí)刻不需要迭代計(jì)算,但在多個(gè)時(shí)刻需要4～6次迭代,而在少數(shù)時(shí)刻需要7～8次迭代。根據(jù)圖1所示的流程,該迭代過(guò)程的最大計(jì)算量為測(cè)量預(yù)測(cè)向量協(xié)方差矩陣Sk的計(jì)算,為此該迭代并不會(huì)引入較大的計(jì)算負(fù)擔(dān)、進(jìn)而可以保證算法的實(shí)時(shí)性。

4 結(jié)論

研究結(jié)果表明,相對(duì)于已有算法,文中算法能夠更有效抑制非高斯測(cè)量噪聲及測(cè)量異常的影響,相對(duì)于KF和RKF算法,IRKF算法可提高位置精度分別為14.1%和8.1%,可提高速度精度分別為13.8%和7.7%,進(jìn)而提高了組合導(dǎo)航系統(tǒng)的濾波精度,并為復(fù)雜環(huán)境下組合導(dǎo)航系統(tǒng)信息融合算法提供了有效途徑。同時(shí),文中算法與表1中所設(shè)定的導(dǎo)航參數(shù)無(wú)關(guān)聯(lián)關(guān)系,當(dāng)IMU參數(shù)改變時(shí)該算法也同樣適用。

由于文中是通過(guò)牛頓迭代法求解比例因子,而牛頓迭代法需要的迭代次數(shù)可能較大,下一步的研究重點(diǎn)是通過(guò)解釋法求得比例因子。