基于差分進化粒子群混合算法的多無人機協同區域搜索策略

賴幸君，唐 鑫，林 磊，王志勝，叢玉華

(1 國家無線電監測中心檢測中心，北京 100041；2 南京航空航天大學自動化學院，江蘇 南京 210016)

0 引言

無人機是一種可自主控制或通過無線電控制的無人駕駛航空器,與有人駕駛飛機相比,無人機具有成本低、體積小、機動性強、部署方便、在高危環境下無人員傷亡等優點[1],目前已被廣泛應用于搜索、遙感、勘探等領域[2-6]。

目前針對未知區域的全區域覆蓋和針對已知目標信息的搜索問題已有了大量研究,但對于未知環境的目標搜索問題研究相對較少。全區域覆蓋方面,Muoz等[7]針對在雜亂的城市環境中執行區域覆蓋任務時可能產生碰撞的問題,建立了考慮城市中障礙物的地圖模型,并基于無沖突領航路徑和領航-跟隨者編隊策略,計算所有無人機的路徑。Chen等[8]針對異構無人機群在多個獨立的區域進行大規模協作搜索任務時,計算復雜度高,難以求解的問題,提出基于蟻群算法求解近似最優的區域覆蓋路徑。Zhang等[9]針對多無人機在大范圍區域中的覆蓋問題,將該區域分解為可以被無人機相機完全覆蓋的若干正三角形,并將需要覆蓋的目標區域轉換為由節點和邊組成的連通圖,并采用混合線性整數規劃法來求解無人機的區域覆蓋航路規劃問題。

目標搜索問題的思想與區域覆蓋相反,其主要目標為:用盡可能短的時間搜索到區域內的目標,減少多余搜索。Zhou等[10]為了在提高無人機搜索目標效率的同時,能躲避環境中的障礙物,提出了一種免疫遺傳算法,并在返程階段,設計了一種分而治之和確定性路徑優化算法,解決無人機完成任務后的返程問題。Duan等[11]針對多無人機執行空中搜索任務的優化指標建立問題,利用貝葉斯公式構造和更新概率圖,指導無人機的搜索。Yu等[12]針對災害場景中的目標搜索問題,將無人機的飛行距離和航跡的風險加入考慮范圍,使無人機能完成目標搜索任務的同時,減少無人機執行任務過程中發生意外的概率。

根據搜索任務需求提出的優化問題,設計合適的優化算法求解無人機的搜索路線是解決區域搜索問題的關鍵。由于待搜索環境往往有很大的不確定性,離線規劃的算法在區域搜索問題中并不適用,需要無人機根據實時變化的環境調整搜索路線,這對算法的實時性要求較高。目前主流的算法主要有啟發式算法(模擬退火法、遺傳算法、蟻群算法、粒子群算法、狼群算法等)和人工智能優化算法(深度學習、強化學習等)[13]。啟發式算法由于其在規定時間內必然可以給出可行解、且不依賴于模型的特點,被研究者們用于無人機實時決策問題上。Ghambari等[14]將幾種典型的自然啟發式算法應用于帶約束的路徑規劃問題,為啟發式算法在帶約束問題中的應用提供了參考。Cho等[15]為搜索問題建立了混合整數線性規劃模型,并開發了一種隨機搜索啟發式算法,減少計算時間的同時,保證了搜索方案的最優性。Zhu等[16]提出了一種分布式在線啟發式策略,在其中融合了并行搜索和內螺旋搜索等幾何特征,在多無人機協同區域覆蓋問題中取得了較高的搜索效率。Han等[17]在考慮避障的區域覆蓋路徑規劃問題中引入蟻群算法,在規劃的路徑長度和能耗方面取得了很好的性能。Kyriakakis等[18]針對無人機搜索和救援場景的動態優化問題,提出了一種多群框架,將多種群智能算法用于求解該問題,證明粒子群算法是眾多算法中最有效的群智能算法。

綜上分析,現有國內外研究雖然在多無人機協同區域搜索決策方法上有一定的研究,但仍存有以下問題有待研究解決:1)現有的區域搜索方法考慮的因素不夠全面,當綜合考慮多項優化指標后,傳統的群智能優化算法求解區域搜索問題易陷入局部最優,導致搜索性能不佳;2)傳統群智能優化算法在求解復雜多目標優化問題時尋優時間更長,實時性較差。

針對以上問題,開展了以下研究:首先為了提高多無人機協同區域搜索綜合性能,將區域覆蓋率、區域不確定度、目標發現概率加入優化目標,作為衡量區域搜索性能的指標;其次提出一種基于差分進化粒子群混合算法的無人機區域搜索策略,提高搜索性能和尋優效率;最后通過充分的仿真實驗,驗證所提算法在多無人機協同區域搜索問題中的性能。

1 問題描述

文中主要針對區域內目標數量NT未知,區域內目標分布情況未知的場景下,NU架無人機飛入待搜索區域,利用自身攜帶的傳感器對區域進行自主搜索,根據無人機獲得的區域地圖信息,在線自主決策,在規定的任務時間內,盡可能多地發現未知目標,并覆蓋盡可能多的未知區域,從而掌握區域內的信息。任務的示意圖如圖1所示。

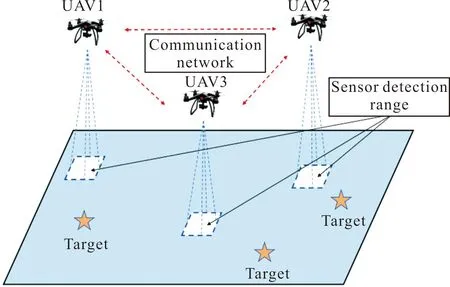
圖1 多無人機區域搜索任務示意圖Fig.1 Multi-UAV area search mission diagram

1.1 搜索環境模型

在多無人機區域搜索場景中,NU架無人機對區域內的NT個目標進行搜索和位置確認。無人機用Ai(1≤i≤NU)表示,待搜索目標用Tj(1≤j≤NT)表示。

將待搜索區域Ω離散成網格圖[19-21],如圖2所示。網格圖由Lx×Ly個網格構成,每個網格的長和寬分別為Δx和Δy。根據網格圖建立二維坐標系,第m行第n列的網格中心的坐標為(m,n),其中1≤m≤Lx,1≤n≤Ly。

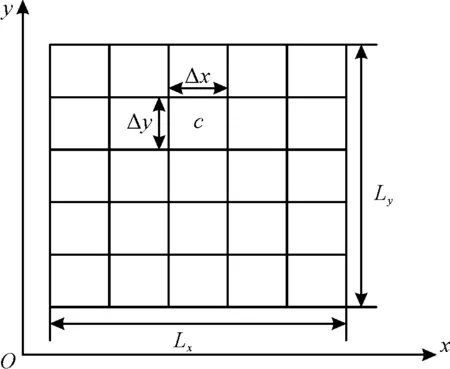
圖2 網格化后的待搜索環境Fig.2 Environment to be searched after gridding

假設每個網格中最多存在一個目標,那么網格中的目標存在情況可表示為:

sc={(xc,yc,ξc)|c∈Ω}

(1)

式中:xc和yc分別為網格c的x軸坐標和y軸坐標;ξc為網格c處的目標存在狀態。ξc可表示為:

(2)

文中采用旋翼無人機執行區域搜索任務。由于傳感器的檢測性能受無人機飛行高度影響,為了便于無人機判斷,將無人機設為固定高度,從而使無人機機載傳感器的探測范圍固定。無人機的運動學模型簡化為:

(3)

式中:xi(t),yi(t)為無人機的空間坐標;Vi(t)為無人機i的飛行速度;φi(t)為無人機i飛行方向與x軸正方向的夾角;ωi(t)為無人機轉彎時的角速度。

無人機基于式(3)所示的運動模型在待搜索區域中運動,航向角φi可為[-180°,180°]區間內的任意值,速度Vi(t)需滿足無人機最大飛行速度約束,即Vi(t)≤Vmax。無人機在空中的飛行時間需滿足無人機最大續航時間,即t≤tmax。

1.2 區域信息地圖

為準確反映無人機對區域的搜索情況,下面建立無人機的目標存在概率圖模型、區域不確定度地圖模型、區域覆蓋圖模型。

1.2.1 目標存在概率圖

根據任務環境的地形與目標類型,建立目標存在概率圖。隨著無人機搜索的進行,無人機對區域內的探測結果會影響后續對目標位置的判斷,每架無人機建立目標存在概率地圖[22]可表示為:

Mi,prob(k)={pi,c(k)|c∈Ω}

(4)

式中pi,c(k)為無人機i的概率地圖中網格c處的目標存在概率。

根據貝葉斯公式[23],更新k時刻在無人機視場范圍內的網格的目標存在概率pi,c(k)為:

(5)

式中:pd為無人機的探測概率;pf為無人機的虛警概率;Φi,k為無人機的傳感器探測范圍,若k時刻無人機i在網格c中發現目標,無人機的探測結果表示為Wi,c(k)=1,反之,探測結果表示為Wi,c(k)=0。

1.2.2 區域不確定度地圖

為了將無人機對網格的信息認知程度量化,以反映無人機是否了解區域中的目標存在情況,引入區域不確定度ηi,c(k),建立區域不確定度地圖[24]:

(6)

式中Kη>0,為常數。根據式(6)與式(7)可以得出區域不確定度ηi,c(k)與目標存在概率pi,c(k)的關系。

1.2.3 區域覆蓋地圖

為了準確表示待搜索區域中被無人機搜索過的區域面積,文中用區域覆蓋狀態Cc(k)表示無人機對網格c的覆蓋情況:

(7)

根據整個區域網格覆蓋狀態,可以將無人機對環境的區域覆蓋率[25]C(k)表示為:

(8)

式中Gall為環境網格地圖中的網格總數。

2 多無人機協同區域搜索策略

2.1 無人機區域搜索滾動時域優化模型

在無人機區域搜索問題中,由于環境的未知與多變性,離線解算的結果無法適應動態變化的環境,因此,文中借鑒模型預測控制中的滾動時域優化思想[26-30],建立小規模優化目標,無人機只需求解預測的時間窗范圍內的最優動作,降低計算的難度。無人機的滾動時域優化模型可表示為:

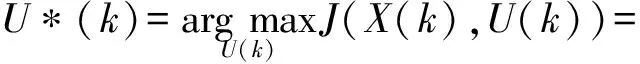
(9)

式中:U*(k)為決策的控制輸入序列;U(k)={u(k),u(k+1),…,u(k+tw)}為無人機在動態時間窗內的輸入決策序列;tw為動態時間窗長度;X(k)為k時刻的狀態輸入,包括k時刻的區域覆蓋圖、目標存在概率圖、區域不確定度地圖以及所有無人機的位置信息、能量消耗情況;Jc,Jp,Ju分別為區域覆蓋率目標函數、目標發現概率目標函數、區域不確定度目標函數;Je為無人機能量消耗代價函數,用于減少無人機在搜索過程中的能量消耗;λc,λp,λu,λe分別為四種優化目標對應的權重系數。

2.2 基于差分進化粒子群混合算法的無人機區域搜索策略

為了防止無人機的搜索路線過早陷入局部最優,對差分進化算法(DE)和粒子群優化算法(PSO)取長補短,提出基于差分進化粒子群混合算法(PSODE)的區域搜索策略,求解所提出的多目標優化問題。PSODE算法的尋優過程如圖3所示。

基于PSODE算法規劃無人機搜索路線的總體步驟如下:

步驟1:分別為DE算法和PSO算法產生n個初始隨機解Ui,de(k)、Ui,pso(k),i=1,2,…,n(即為無人機的控制決策輸入)。

(10)

式中:Ui,pso(k)為粒子群算法解集中第i個解(簡稱為粒子i);Vi為粒子i的更新速度;Gbest(k)為k時刻Ui,pso(k)中的全局最優解;c1,c2分別為個體學習因子和群體學習因子;r1,r2為區間[0,1]內的隨機數;w為慣性權重,表示當前迭代輪次受上一輪迭代速度的影響程度。根據Gbest(k)計算出粒子群算法中的最優適應度函數fpso。

步驟4:比較fde,fpso,取其最大值作為全局最優適應度fpg,計算DE算法與PSO算法的選擇概率pselde,pselpso,其中DE算法的選擇概率計算公式為:

(11)

其中,λ1和λ2的計算方式分別為:

(12)

(13)

相對應的,PSO算法的選擇概率為:

pselpso=1-pselde

(14)

步驟5:產生0～1之間的隨機數Nrand,若Nrandpselde,則選用PSO算法,按步驟3的方式更新Ui,pso(k)。

步驟6:若未達到設定的最大迭代次數,則按步驟5的方式不斷更新Ui,de(k);Ui,pso(k);否則,比較fde與fpso,若fde>fpso,則選用Ui,de(k)作為無人機的控制輸入;否則,將Ui,pso(k)作為無人機的控制輸入。

為了讓算法能在收斂速度和尋優精度取得均衡,文中對算法中的PSO算法和DE算法均采用自適應參數調整的策略。

在PSO算法中,種群的更新速度和精度主要受慣性權重w影響,文中對w采用線性遞減策略,w的更新公式為:

(15)

式中:wmax為慣性權重的最大值;wmin分別為慣性權重的最小值;Nmaxit為最大迭代次數。

在DE算法中,變異因子F是影響其種群更新的關鍵參數。在進化早期,種群應擴大搜索范圍尋找最優解,此時F的值應較大,隨著進化過程的進行,F的值應逐漸變小,由全局搜索轉變為以局部搜索為主,精準尋優。因此,DE算法的變異因子F采用如下的自適應調整方式:

(16)

式中,Fmax與Fmin分別為最大變異因子和最小變異因子。

3 仿真分析

為驗證基于PSODE算法的無人機區域搜索策略的有效性,首先,在相同環境下,對比基于PSODE算法的無人機區域搜索策略與單一的PSO算法、DE算法的性能差異;其次,進行多次實驗,對比三種算法的性能指標平均值與方差,驗證算法的穩定性;最后分析迭代次數對算法性能的影響,驗證提出的PSODE算法在實時性方面的性能。

3.1 仿真參數設置

設置環境未知的待搜索區域大小為30 km×30 km,將待搜索區域進行網格化處理,將區域劃分為30×30的網格圖,執行任務的無人機數量為3,無人機的初始位置分別為(2 km,2 km)、(28 km,2 km)、(2 km,28 km),無人機攜帶的傳感器探測概率pd為0.8,虛警概率pf為0.2,認為網格中存在目標的概率閾值設置為0.9;設置執行未知區域搜索任務的時間為30 min,無人機的能耗模型參考文獻[30]。優化算法的參數設置方面,PSO算法的初始慣性系數wstart為0.8,末尾慣性系數wend為0.2,更新速度Vd范圍限制設置為[-1,1],個體學習因子c1與群體學習因子c2均為0.25。DE算法的初始變異因子Fmax為0.65,末尾變異因子Fmin為0.3,交叉概率CR為0.9;PSODE算法的參數與PSO算法和DE算法的參數均相同。

3.2 算法計算結果分析

分別采用DE算法、PSO算法和PSODE算法求解多無人機協同區域搜索問題,三種算法的搜索結果圖如圖4～圖6所示,DE算法在任務過程中會產生較多的重復搜索,導致搜索效率不高,有大片區域未被搜索。基于PSO算法的無人機區域搜索策略在搜索后期,無人機會存在重復搜索的問題。PSODE算法重復搜索的頻率比PSO算法和DE算法更低,搜索結束時對區域的覆蓋率更高,可將區域不確定度降至更低。

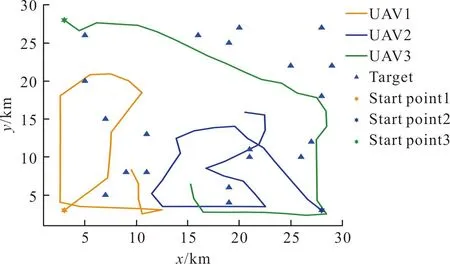
圖4 基于DE算法的搜索結果圖Fig.4 Search result graph based on DE algorithm

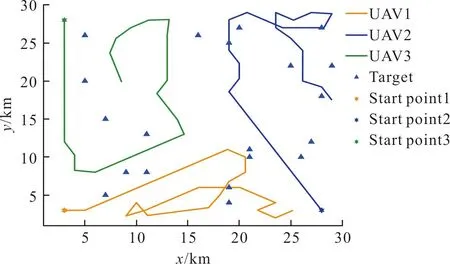
圖5 基于PSO算法的搜索結果圖Fig.5 Search result graph based on PSO algorithm

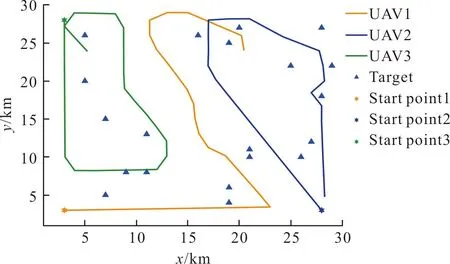
圖6 基于PSODE算法的搜索結果圖Fig.6 Search result graph based on PSODE algorithm

無人機在搜索結束時的區域覆蓋率、區域不確定度與消耗的總能量對比如表1所示。文中提出的PSODE算法可達到97.26%的區域覆蓋率,分別比PSO算法和DE算法高1.59%、10.04%;搜索完成后的區域不確定度方面,提出的PSODE算法分別比另外兩種算法低2.46%、9.87%,對區域的信息掌握程度更高;用于轉彎消耗的能量分別比PSO算法和DE算法少57.74%、61.25%;發現目標數方面,三種算法幾乎相同。綜合四項性能指標可以看出,基于PSODE算法的區域搜索策略在相同條件下,具備更好的搜索性能。

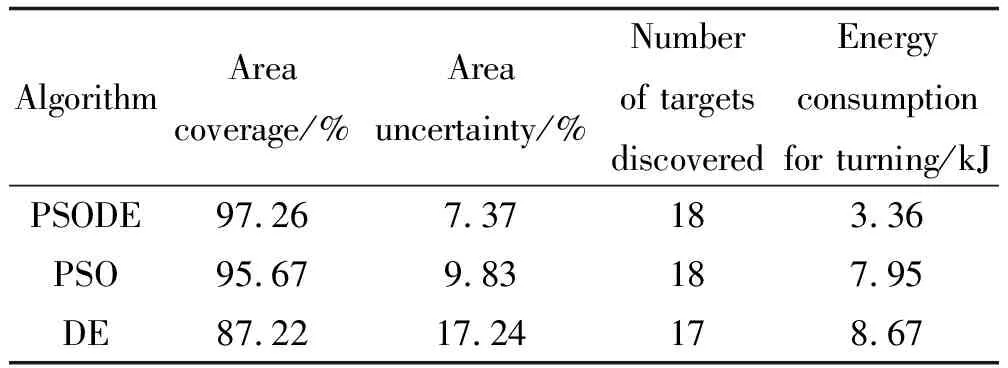
表1 三種算法的區域搜索結果性能比較Table 1 Performance comparison of area search results for three algorithms

3.3 迭代次數對算法性能的影響分析

由于無人機需要在線決策搜索路線,因此對算法的實時性要求較高,本節對不同迭代次數下三種算法的區域搜索性能進行量化分析,驗證迭代次數對算法性能的影響。分別設置算法的迭代次數為20,50,100,在相同環境中進行次數為20仿真實驗,對比結果如圖7和表2所示。

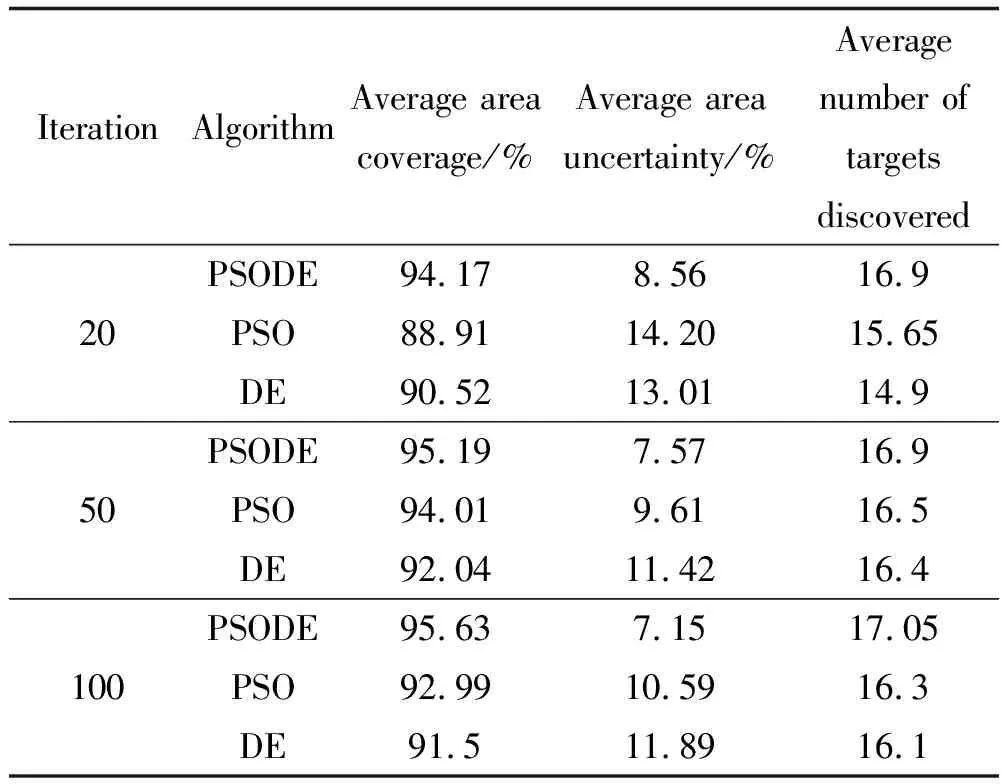
表2 不同迭代次數下三種算法的性能指標情況Table 2 Performance indexes of the three algorithms with different number of iterations

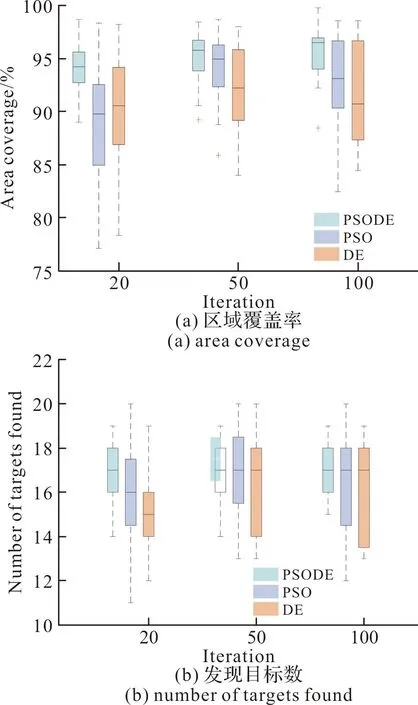
圖7 不同迭代次數下三種算法的性能指標情況Fig.7 Performance metrics of the three algorithms with different iterations

由圖7可知,相同迭代次數下,文中提出的基于PSODE算法的區域搜索策略各項性能指標的方差比其他兩種未改進的算法小,在區域搜索過程中表現出的性能更穩定。

表2為仿真實驗中算法不同迭代次數的平均性能指標,由數據可以看出,隨著迭代次數的提升,三種算法的性能指標均有不同程度的提高,基于PSODE算法的區域搜索策略在迭代次數20時,平均區域覆蓋率就已經達到94.17%,比另外兩種算法高5.26%,3.65%,區域不確定度降低至8.56%,比其他兩種算法低5.64%、4.45%,平均發現目標數為16.9,分別比其他兩種算法多1.25、2,且PSODE算法在迭代次數20時,便已獲得比其他兩種算法100次迭代時更優的性能,由此可見基于PSODE算法的區域搜索策略具備更好的實時性。

3.4 目標函數權重系數影響分析

在提出的滾動時域優化模型中,λc,λp、λu與λe分別表示無人機執行區域搜索任務時對區域的覆蓋率、發現目標概率、區域不確定度和無人機能量消耗四個方面的權重,為了驗證不同的權重對無人機區域搜索策略的影響,將權重系數按表3中的組合分別進行仿真分析。

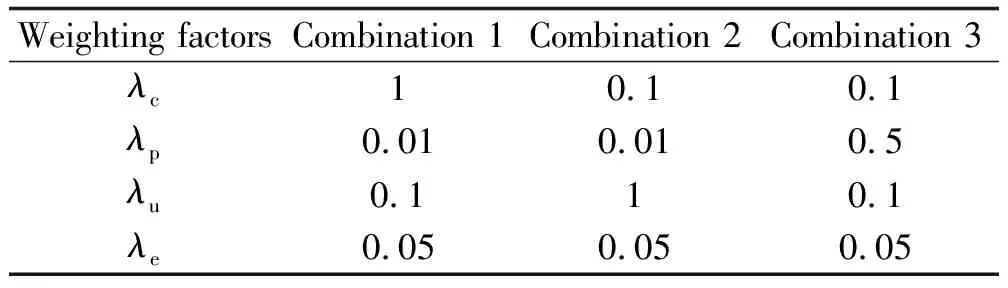
表3 無人機區域搜索優化目標權重系數組合Table 3 Combination of target weight coefficients for UAV area search optimization

三種權重組合的航跡圖如圖8所示。在待搜索區域中,紅色區域和綠色區域為無人機開始搜索前,根據已知的地形推測出的部分已知目標存在概率的區域,其中紅色區域表示目標存在概率為0.8,綠色區域表示目標存在概率為0.2,其他區域的信息完全未知,目標存在概率為0.5。三種權重組合分別對應了不同的任務需求。

圖8 不同權重系數下無人機區域搜索航跡Fig.8 UAV regional search trajectory with different weighting factors

搜索性能的指標變化曲線如圖9所示。在區域覆蓋率方面,組合1權重下的區域搜索策略,獲得的區域覆蓋率最高,為95.56%,分別比組合2和組合3高20.56%、18.00%,;在區域不確定度方面,組合2的不確定度下降速度更快,任務完成時,組合2與組合1的區域不確定度分別為6.15%、6.21%,分別比組合3低11.64%、11.58%;無人機搜索區域的目標存在概率方面,權重組合3的搜索路線會優先搜索目標存在概率高的區域,搜索過的區域目標存在概率總和曲線上升速度比組合1和組合2快。在實際應用時,可選擇不同的權重組合以適應不同的任務需求。

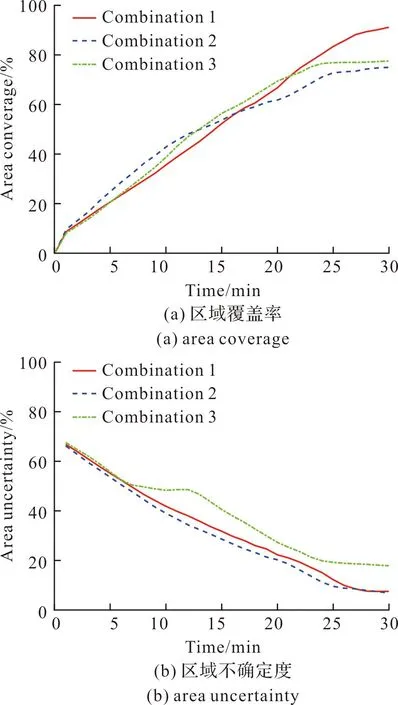
圖9 不同權重系數無人機區域搜索性能指標變化曲線Fig.9 Change curve of UAV area search performance index under different weighting factors

4 結論

文中針對未知環境下的無人機區域搜索問題,提出基于差分進化粒子群混合算法的無人機區域搜索策略,解決了現有的區域搜索方法總體性能不佳、實時性差的問題,從區域覆蓋率、目標發現概率、區域不確定度和能量消耗4個方面提升了無人機區域搜索性能,從仿真結果可以看出,所設計的基于差分進化粒子群混合算法的無人機區域搜索策略可獲得比基于粒子群算法、差分進化算法的區域搜索策略更優的搜索性能,并具備較好的實時性和穩定性。然而,文中提出的區域搜索策略未考慮無人機在環境中可能遇到意外事件損毀的情況,未來計劃將無人機損毀情況加入考慮范圍,使區域搜索策略可適應更為復雜的環境。