新型過載駕駛儀滾轉彈制導系統穩定性研究

李 濤，付 博，王齊雙，段辰璐，林時堯

(1 西安現代控制技術研究所，陜西 西安 710065；2 中國兵器科學研究院，北京 100089)

0 引言

隨著世界新軍事革命的深入,制導武器遠程化、精確化、信息化已成為現代常規戰爭的趨勢[1-4]。對于采用旋轉體制的制導武器,由于減少了傳感器數量從而簡化了控制系統組成。此外,旋轉削弱了激光攔截武器的打擊,并可以主動借助錐形運動引起的螺線彈道進行機動突防[5]。錐形運動的誘因主要包括彈體自身的慣性陀螺效應、外形結構不對稱和氣動Magnus效應等動不平衡因素。

自從20世紀50年代以來,旋轉彈體錐形運動的研究一直備受國內外學術界關注。早在1953年,Nicolaides就指出旋轉彈體存在二圓運動特征,隨著章動角的增大,彈體以螺旋前進的方式飛行,同時指明旋轉彈體應避免轉速閉鎖導致的災變性偏航問題[6]。Thomson指出錐形運動的回轉軸為彈體的最小主慣性軸時,系統存在由能量耗散導致的錐形運動發散的趨勢[7]。之后,Murphy面向無控旋轉彈體,采用一階線性化策略得出了系統動態穩定域,得出面外力矩不僅引起一個圓運動收斂,還會導致另一個圓運動的發散[8]。此外,Morote分析了旋轉彈體卷弧翼帶來的氣動特性,指出翼面產生的馬格努斯效應是導致錐形運動發散的一個重要原因[9]。針對錐形運動降低制導精度問題,現有研究表明應該使關鍵設計變量遠離不穩定區域,而對臨界狀態鮮有開展更深層的研究[10-11]。

在錐形運動應對措施方面,研究表明被動削弱彈體錐形運動的成效十分有限[12]。Javier等提出在彈體前端增設一對獨立的可伸縮翼片來主動抑制錐形運動[13]。Platus提出通過姿態角反饋控制方式來增加彈體固有頻率,以補償彈體滾轉導致的錐形共振,使彈體遠離轉速閉鎖區域[14]。采用主動抑制法的關鍵問題在于執行機構能否及時準確地響應指令,否則可能加劇錐形運動。此外,彈體自旋會引起偏航與俯仰通道之間嚴重的交叉耦合作用,因而采用傳統分通道設計自動駕駛儀難以確保彈體錐形運動穩定性。針對此問題,Yan等建立了考慮慣性耦合、氣動耦合以及控制耦合的滾轉彈體姿態運動模型,同時按照非旋轉彈體控制回路拓撲思路設計出旋轉彈體姿態駕駛儀和阻尼控制回路,并且推導出控制系統穩定性條件[15-16]。Li等基于旋轉彈的經典三回路駕駛儀的回路拓撲結構,推導出系統的穩定性設計準則[17-18]。Zheng等研究了雷達制導滾轉導彈錐形運動的動態穩定性,提出了一種考慮天線罩寄生回路的復合數學模型,推導了滾轉導彈錐形運動動態穩定性的充要條件[19]。Tian等基于復變形式的微分方程,獲得了考慮寄生效應的偽攻角反饋三回路自動駕駛儀滾轉彈穩定性的充要條件[20]。

現有考慮隔離度寄生回路的滾轉彈錐形運動穩定性的研究中,主要引入經典三回路/偽攻角反饋三回路等常見過載駕駛儀,分析雷達導引頭天線罩誤差/捷聯導引頭慣性器件標度因數偏差導致的導引頭隔離度問題。但基于增穩回路直接采取加速度反饋的新型三回路過載駕駛儀,開展滾轉彈錐形運動動態穩定性的研究較少。文中針對上述問題,基于平臺圖像導引頭干擾力矩引起的隔離度寄生回路,分析推導了考慮寄生效應的加速度反饋增穩新型駕駛儀滾轉彈體穩定性條件,進一步分析隔離度、總延遲角和加速度計安裝位置等滾轉彈重要參數對包含隔離度寄生回路的滾轉彈體動態穩定域的影響,為包含隔離度寄生回路的多種回路拓撲結構過載駕駛儀制導系統的動態穩定性研究提供理論參考。

1 數學建模

1.1 滾轉彈動力學模型

為研究存在隔離度寄生回路情況下的滾轉彈體動態穩定性問題,依據文獻[16-18],引入非滾轉框架下滾轉導彈的六自由度動力學方程:

(1)

通過定義復角度αc=β+jα和δ=δv+jδz,可以得到滾轉導彈的線性化復微分方程:

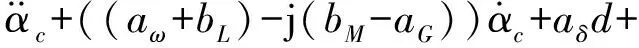
(2)

1.2 新型駕駛儀滾轉彈制導系統模型

在經典三回路過載駕駛儀結構中,中間增穩回路的信號采取角速率的積分。在文獻[21]提出的新型三回路駕駛儀結構中,增穩回路直接采用加速度計的測量信號,其結構如圖2所示,下面基于該新型過載駕駛儀開展滾轉彈制導系統穩定性研究。

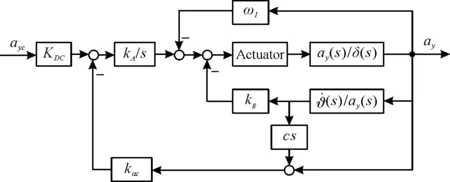
圖2 新型過載駕駛儀Fig.2 New overload autopilot

基于滾轉彈制導原理,引入圖2所示的新型駕駛儀模型與隔離度Rd,建立圖3所示的考慮隔離度寄生回路的新型駕駛儀滾轉彈制導系統模型。

圖3 包含隔離度寄生回路的新型駕駛儀滾轉彈制導模型Fig.3 Guidance model of the new autopilot considering disturbance rejection rate

2 新型駕駛儀滾轉彈制導系統動態穩定條件推導

因為存在隔離度寄生回路,滾轉彈的動態穩定性不僅取決于新型駕駛儀,還會受隔離度Rd、導航比N以及彈目相對接近速度Vc的影響。考慮隔離度寄生回路的新型駕駛儀制導指令可表示為:

(3)

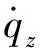
(4)

通過定義復角δc=δyc+jδzc和φ=ψV+jθ,則舵機的指令可表示為:

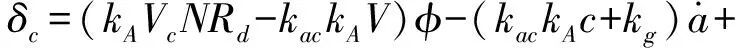
(5)

滾轉彈的俯仰與偏航通道的舵機動力學采取二階動力學模型,舵機輸出與輸入間的關系表示為:

δ=kskr(-δzcsinγd+δyccosγd)+
jkskr(δzccosγd+δycsinγd)=
kskr(cosγd+jsinγd)δc

(6)

基于獲得的復數模型,可使用復系數系統穩定性判據來推導滾轉導彈的動態穩定性條件。將式(5)代入到式(6)中,可得:

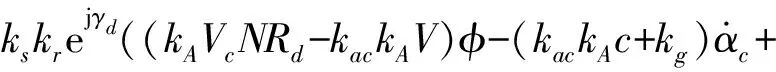
(7)

將式(7)代入式(2)可得:

(8)

(9)

制導系統對應的特征方程為:

(10)

根據附錄A,PN/新型駕駛儀滾轉彈體制導系統穩定的充分必要條件為:

(11)

3 動態穩定條件仿真驗證

3.1 隔離度寄生回路對動態穩定條件的影響

為驗證所推導的穩定條件,滾轉彈的參數如表1所示。在仿真中的其他參數設置為:ω=8π rad/s,N=4,kac=0.0017,C=0,α0=4°。

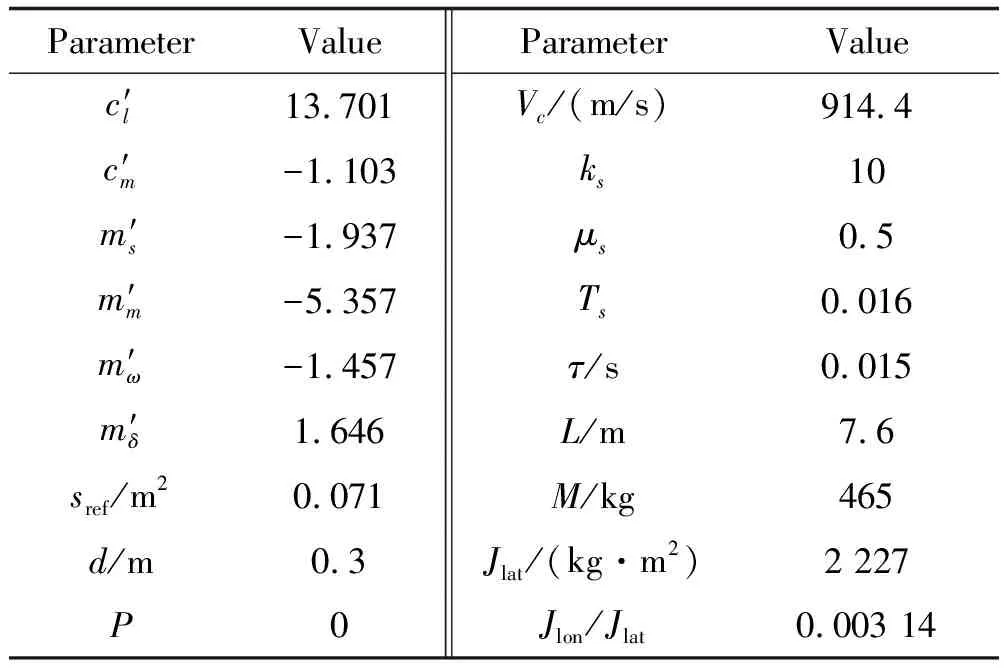
表1 滾轉彈參數設置Table 1 Parameter setting of rolling missile

3.1.1 不考慮隔離度寄生回路

不考慮隔離度寄生回路,此時駕駛儀決定了PN/新型駕駛儀滾轉彈體制導系統的穩定性。按照設計新型駕駛儀的穩定條件,設計參數選取為:kA=0.0088,kg=0.14,ωI=0.0315。則初始擾動α0=4°作用下,不考慮隔離度寄生回路的PN/新型駕駛儀滾轉彈體制導系統仿真結果如圖4所示。

圖4 不考慮隔離度寄生回路的滾轉彈穩定狀態Fig.4 Stable state of rolling missile disregarding disturbance rejection rate

若不考慮隔離度寄生回路,在初始擾動影響下系統狀態逐漸收斂至零,說明新型駕駛儀設計參數可消除由初始攻角誤差引起的錐形運動,從而保證滾轉彈的動態穩定。此外,由于俯仰與偏航通道存在交聯耦合,縱向平面內的初始攻角誤差會引起側向平面的運動。

3.1.2 考慮隔離度寄生回路

當考慮隔離度寄生回路時,PN/新型駕駛儀滾轉彈體制導系統的穩定性取決于制導系統參數。選用滿足新型駕駛儀穩定的設計參數,即kA=0.0088,kg=0.14,ωI=0.0315。分別選取了NVcRd=50,NVcRd=367兩種情況進行仿真驗證,結果如圖5～圖6所示。

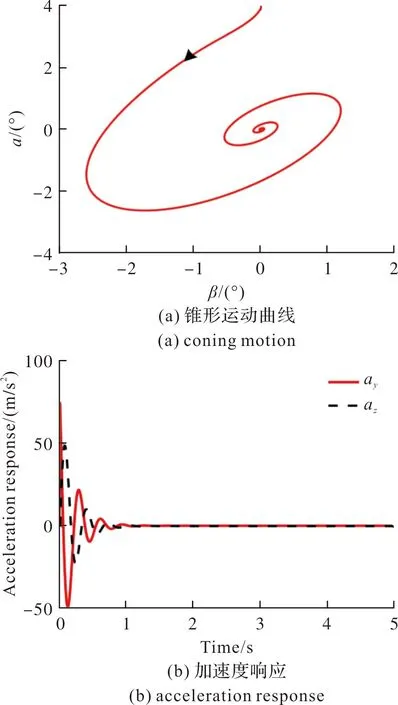
圖5 NVcRd=50時滾轉彈穩定狀態Fig.5 Stable state of rolling missile considering NVcRd=50

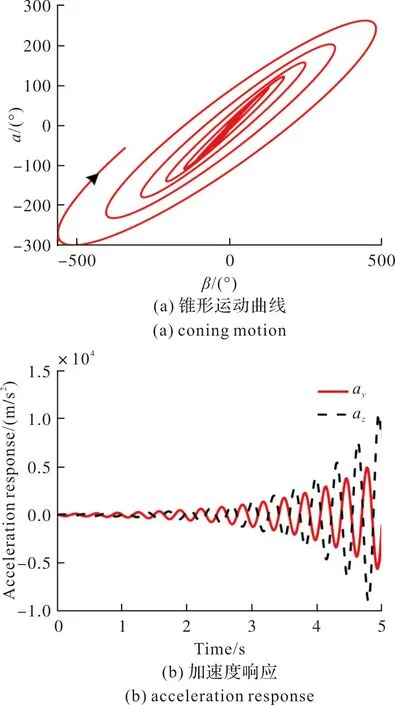
圖6 NVcRd=367時滾轉彈失穩狀態Fig.6 Instable state of rolling missile considering NVcRd=367

隔離度在一定程度上延緩了制導系統的響應速度。當NVcRd=50時,隔離度組合參數滿足穩定性的限制條件,在初始擾動α0=4°影響下,制導系統快速收斂至零;當NVcRd=367時,隔離度組合參數超出穩定性限制邊界,初始擾動影響下制導系統發散。

3.2 制導系統參數對動態穩定條件的影響

新型過載駕駛儀制導系統的穩定性會受隔離度寄生回路組合參數的影響,合理選取新型過載駕駛儀設計參數及其他制導系統參數,可減弱隔離度的不良影響,從而抑制制導系統發散、提升制導系統響應速度。

3.2.1 不同駕駛儀參數對動態穩定條件的影響

選取滾轉彈轉速為ω=8π rad/s,導航系數N=4,駕駛儀加速度反饋增益kac=0.0017,彈體參數見表1。求得不同駕駛儀設計參數穩定域如圖7所示。

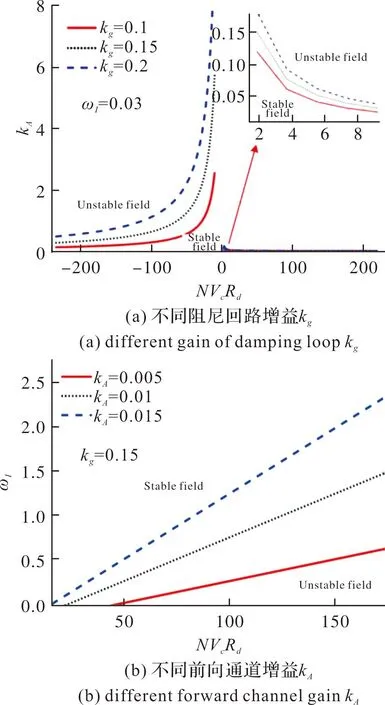
圖7 新型駕駛儀參數穩定域Fig.7 New autopilot parameter stability region

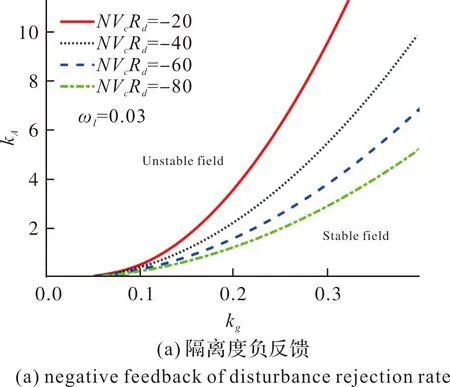
圖8 隔離度對新型駕駛儀參數穩定域的影響Fig.8 The influence of disturbance rejection rate on the new autopilot parameter stability region

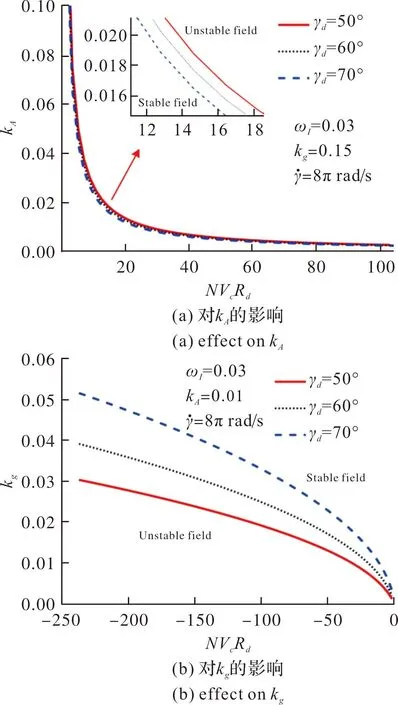
圖9 總延遲角對參數穩定域的影響Fig.9 Influence of total delay angle on parameter stability region

增大前向通道增益kA,將會減小系統參數穩定域;增大阻尼回路增益kg,將會增加系統參數穩定域。此外,隨著隔離度組合參數NVcRd絕對值的增大,系統參數穩定域減小。

3.2.2 不同隔離度對動態穩定條件的影響

對于包含隔離度寄生回路的PN/新型駕駛儀制導系統,隔離度無論是負反饋還是正反饋,都將減小系統參數的穩定域;同時,隨著隔離度絕對值的增加,設計的前向通道增益kA越小。

3.2.3 不同總延遲角對動態穩定條件的影響

總延遲角對新型駕駛儀前向通道增益kA的影響很小,甚至可以忽略;總延遲角越大,設計的阻尼回路增益越大,從而保證彈體有足夠的阻尼維持穩定。

3.2.4 不同加速度計位置對動態穩定條件的影響

選取滾轉彈轉速為ω=8π rad/s,導航系數N=4,設計臨界穩定參數為:加速度計位置C=0,加速度反饋回路增益kac=0.0017,增穩回路增益ωI=0.0315,阻尼回路增益kg=0.14,前向通路增益kA=0.0088,隔離度組合參數NVcRd=209。基于以上設計參數進行仿真,結果如圖10所示。

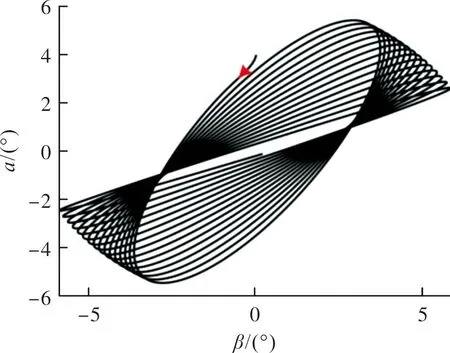
圖10 C=0時臨界穩定的錐形運動Fig.10 Coning motion maintain critical stable when C=0

設計的PN/新型駕駛儀系統參數使系統處于臨界穩定的狀態。使用相同的設計參數,改變加速度計的位置,仿真結果如圖11所示。

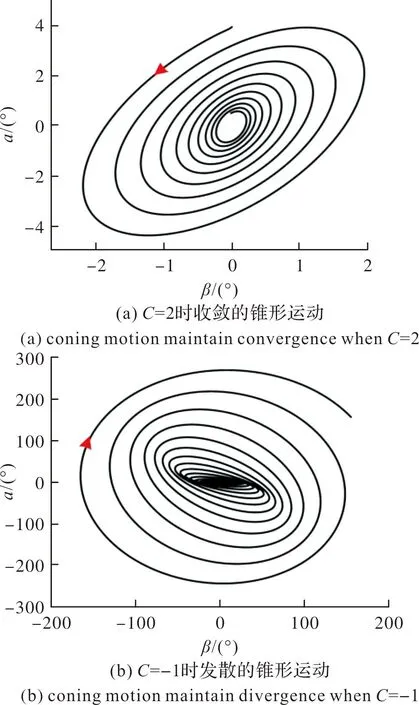
圖11 加速度計位置對穩定性的影響Fig.11 Influence of accelerometer position on stability

當C=2時,即加速度計安裝在彈體質心之前,可使臨界穩定系統趨于穩定;當C=-1時,即加速度計安裝在彈體質心之后,可使臨界穩定系統發散。因此,加速度計安裝在彈體質心之前有利于PN/新型駕駛儀制導系統的穩定。

4 結論

針對制導彈箭錐形運動不穩定導致制導精度變差的問題,基于圖像導引頭干擾力矩引起的隔離度寄生回路問題,開展了滾轉彈動態穩定性研究。分析推導了考慮寄生效應的加速度反饋增穩新型駕駛儀滾轉彈體穩定性條件;系統參數穩定域與隔離度幅值、駕駛儀前向通道增益和舵機總延遲角成反比,與駕駛儀阻尼回路增益成正比。此外,總延遲角主要影響駕駛儀阻尼回路增益的設計,加速度計安裝于質心之前有利于滾轉彈體制導系統的穩定。因此,滾轉效應、寄生效應與控制指令延遲是導致駕駛儀參數設計穩定域減小的主要因素,駕駛儀設計參數應遠離穩定性邊界從而提升錐形運動穩定性。