巧設(shè)Δ用微元思想解決物理問題*
徐清洪 楊 冰
(重慶市第八中學(xué)校 重慶 401120)
1 引言
微元法指將研究過程劃分成多個(gè)微小單元,微小單元依然遵循物理基本規(guī)律,當(dāng)對時(shí)間、位移、轉(zhuǎn)角等物理量取微小單元時(shí),部分相關(guān)物理量在微小單元內(nèi)不會(huì)發(fā)生明顯變化,可以將其處理成定量[1].由于數(shù)學(xué)學(xué)習(xí)的階段性,很多需要應(yīng)用到高等數(shù)學(xué)中微積分知識求解的物理問題成為高中階段的學(xué)生最大的“難題”.但是,如果通過“微元法”把研究對象劃分為無窮多個(gè)小部分,化變力為恒力,化曲線為直線,再從局部到整體就可以很好地解決學(xué)生的困難.下面我們列舉了高中階段3種類型問題,共同特點(diǎn)是采用微元法巧妙設(shè)置Δl、ΔT、Δθ,輕松地避開了繁雜的運(yùn)算過程.
2 問題1:連接體加速度問題
【例1】如圖1所示,將質(zhì)量為 2m 的重物懸掛在輕繩的一端,輕繩的另一端系一質(zhì)量為 m 的小環(huán),小環(huán)套在豎直固定的光滑直桿上,光滑定滑輪與直桿的距離為 d.現(xiàn)將小環(huán)從與定滑輪等高的 O 處由靜止釋放,A 處在 O 處正下方距離為 d 處,則下列說法正確的是 ( )
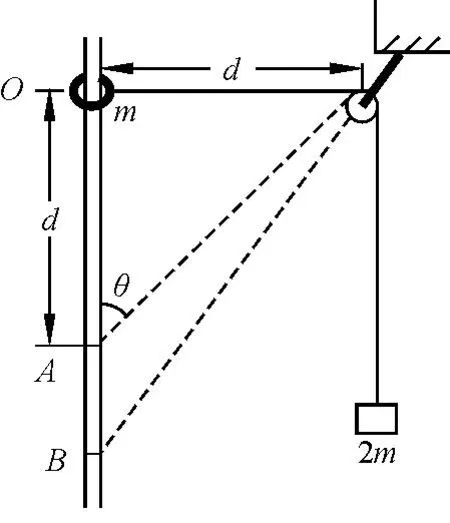
圖1 例1題圖
A.小環(huán)剛釋放時(shí)輕繩中的張力一定大于 2mg
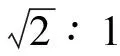
C.小環(huán)下降速度最大時(shí),輕繩中的張力一定等于 2mg
D.小環(huán)從O處開始能夠下降的最大高度為 4d
解法1:定量計(jì)算
判斷選項(xiàng)C正誤方法如下.
本題的難點(diǎn)在選項(xiàng)C判斷,部分學(xué)生會(huì)根據(jù)速度關(guān)聯(lián)得出小環(huán)速度最大時(shí)重物速度也最大,重物加速度為零,張力與重物重力平衡,為解決該疑惑,可設(shè)細(xì)線與桿之間夾角為θ,由關(guān)聯(lián)速度可知
v環(huán)cosθ=v物
上式兩邊對t求導(dǎo)
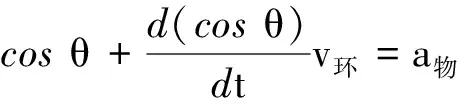
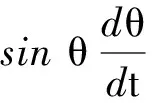
解法2:微元法
取環(huán)速度達(dá)到最大時(shí)附近一小段運(yùn)動(dòng)ABC,將其平均分為兩段,每段長為Δl,由于時(shí)間非常短這一小段運(yùn)動(dòng)可以近似處理成勻速運(yùn)動(dòng),如圖2所示.AB段運(yùn)動(dòng)使定滑輪左側(cè)細(xì)線長度改變量Δx1=Δlcosθ1,BC段運(yùn)動(dòng)細(xì)線長度改變量Δx2=Δlcosθ2,由于θ1>θ2,有Δx2>Δx1,在小環(huán)勻速從A到B到C過程中,細(xì)線長度改變越來越快,物件在加速上升.

圖2 例1分析圖
據(jù)以上分析判斷結(jié)論為:小環(huán)速度最大時(shí),小環(huán)加速度為零,而重物在加速上升,細(xì)線拉力大于2mg.
2 問題2:判斷液柱移動(dòng)方向
【例2】兩個(gè)容器A、B用截面均勻的水平玻璃管相通,如圖3所示,A、B中所裝氣體溫度分別為10 ℃和20 ℃,水銀柱在管中央平衡,如果兩邊溫度都升高10 ℃,則水銀柱將( )

圖3 例2題圖
A.向左移動(dòng)B.向右移動(dòng)
C.不動(dòng)D.無法確定
解法1:定量計(jì)算
假設(shè)溫度升高過程氣體體積不變,為等容變化,壓強(qiáng)與溫度成正比,有
pA=kATApB=kBTB
分析初始狀態(tài)有pA0=pB0,TA0
解法2:微元法
初始狀態(tài),水銀柱在管中平衡左右兩邊氣態(tài)壓強(qiáng)相同均為p0,控制氣體體積不變,將氣體處理成理想氣體,p-T圖為過原點(diǎn)直線,如圖4所示.初始態(tài)左右氣體壓強(qiáng)一樣大,A溫度低于B溫度,A斜率大.兩邊都升高相同溫度,在圖像上以初始溫度值TA0、TB0為起點(diǎn)取相同溫度增量ΔT,A、B壓強(qiáng)增量關(guān)系為ΔpA>ΔpB,平衡打破,液柱向B側(cè)移動(dòng).
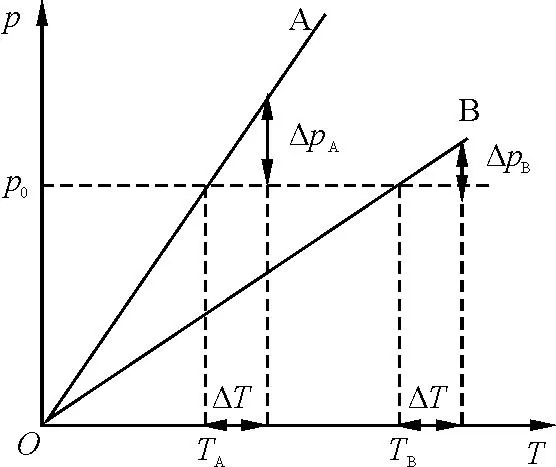
圖4 例2分析圖
3 問題3:2022年山東高考理綜卷第12題


圖5 例3題圖




判斷選項(xiàng)C、D的方法如下.
解法1:定量計(jì)算

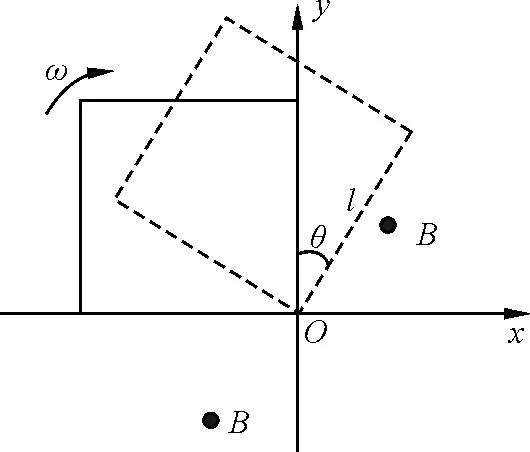
圖6 例3分析圖
其中
對ε隨夾角變化函數(shù)式求導(dǎo)
其中θ=ωt.
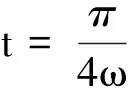
解法2:微元法
從θ=0到θ=45°過程中,將線框旋入磁場過程均分成很多連續(xù)相等小段Δθ,由于線框勻速轉(zhuǎn)動(dòng),Δθ對應(yīng)時(shí)間均為Δt,如圖7所示,取其中第n、n+1、n+2小段旋轉(zhuǎn)運(yùn)動(dòng)為例.
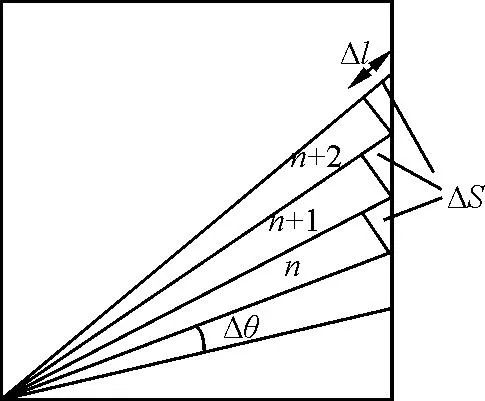
圖7 微元法分析圖
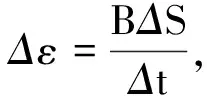
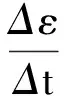
4 結(jié)束語
連接體加速度關(guān)聯(lián)問題、判斷液柱移動(dòng)方向、判斷感應(yīng)電動(dòng)勢變化率變化情況,是高中學(xué)生學(xué)習(xí)過程中不可避免的幾個(gè)重點(diǎn)難題,本文在運(yùn)動(dòng)及變化過程中設(shè)置Δl、ΔT、Δθ,運(yùn)用了微元法的思想,結(jié)合物理圖例圖像解決問題,巧妙、合理地避開了繁雜的運(yùn)算過程,培養(yǎng)了學(xué)生物理科學(xué)思維的同時(shí),提高學(xué)生分析問題、解決問題的能力.

