基于中國場地相關譜的核電廠結構地震易損性與風險研究

王曉磊，閻衛東，呂大剛

(1.沈陽建筑大學土木工程學院，沈陽 110168；2.河北省地震災害防御與風險評價重點實驗室，三河 065301；3.哈爾濱工業大學土木工程學院，哈爾濱 150090)

近年來，我國核電工程得到了快速發展，安全是核電發展的重要前提和基礎。由于實際地震發生或概率地震危險性分析技術的發展，核電廠面臨地震風險水平需要重新進行評估。概率地震風險評估是核工程結構抗震安全評估的重要方法之一[1-2]，概率地震危險性分析與場地相關譜理論與應用發展對精細化概率地震風險評估方法應用起到了促進作用[3]。

場地概率地震危險性分析是核電廠地震風險評估重要步驟之一。CORNELL[4]和MCGUIRE[5]較早給出了場地概率地震危險性分析理論基礎和軟件實現，該分析方法是以單個強度參數為目標的標量型危險性分析(Scalar probabilistic seismic hazard analysis, SPSHA)理論。目前，我國地震安評采用的是以Cornell-McGuire 分析理論[4-5]為基礎的標量型危險性分析方法。WANG 等[6]基于中國地震危險性分析特點，提出了基于蒙特卡洛模擬的中國概率地震危險性分析與分解程序，能夠為中國場地條件均值譜提供危險性分析與分解結果。標量型危險性分析與分解無法考慮不同強度參數間相關性，針對上述不足，BAZZURRO 等[7-8]提出了向量型危險性分析(Vector probabilistic seismic hazard analysis, VPSHA)理論；同時，IERVOLINO等[9]提出了以某個強度參數為條件的條件型危險性分析 (Conditional probabilistic seismic hazard analysis, CPSHA)理論。截至目前，基于中國地震環境特點的中國向量型地震危險性分析與條件型危險性分析方法研究還鮮見報道。

場地相關譜是概率地震危險性分析與分解產物，隨著概率地震危險性分析與分解理論與應用的發展，一些場地相關譜理論也得到了不斷發展。一致危險譜(Uniform hazard spectrum, UHS)[10]是早期被廣泛采用的場地相關譜，該譜的超越概率信息較為明確，但相對比較保守。針對這一情況，BAKER[11]提出了考慮譜型相關性信息的條件均值譜(Conditional mean spectrum, CMS)。WANG等[6]生成了我國某核電廠場地條件均值譜。汪維依等[12]提出了基于“完備”條件譜的我國地震動選取方法。高嘉偉等[13]提出了考慮高階振型影響的模態條件均值譜。一致危險譜較為保守，而條件均值譜譜型較窄，針對上述情況，KISHIDA[14]提出了基于向量型危險性分解結果的廣義條件均值譜(Generalized conditional mean spectrum, GCMS)理論。基于中國地震環境的廣義條件均值譜以及條件型場地相關譜理論研究還鮮見報道。

近年來，隨著概率地震危險性分析與場地相關譜理論研究的發展，基于概率地震危險性與場地相關譜的核電廠結構地震易損性與風險也得到了應用研究：CHOI 等[15]進行了基于一致危險譜的核電安全殼地震易損性研究；HUANG[16]進行了基于條件均值譜的核電廠地震易損性和安全評估研究。KUMAR 等[17]研究了不同地震危險性及場地相關譜定義對核電廠隔震系統位移影響。JIN 等[18]提出了核電安全殼結構概率地震風險評估的一種簡化分析方法，并基于我國華南地區某核電廠場地危險性曲線進行應用研究。BAO 等[19]基于主余震危險性和一致危險譜，進行了安全殼結構時變地震風險評估。

基于廣義條件均值譜及條件型場地相關譜的核電廠結構易損性與風險研究還較缺乏。同時，地震風險評估是地震危險性和地震易損性卷積計算結果，不同場地相關譜定義對核工程結構地震風險評估影響研究還較為缺乏。

本文首先總結了中國場地標量型概率地震危險性分析與分解理論，提出了考慮強度參數間相關性的中國向量型概率地震危險性分析與分解方法，給出了適用于中國場地的條件型概率地震危險性分析理論；然后，基于中國概率地震危險性分析與分解方法，總結了中國場地一致危險譜理論及生成步驟，提出了適用于中國廠址的條件均值譜、廣義條件均值譜和條件一致危險譜生成方法；給出了基于中國場地相關譜的核電廠結構地震易損性與風險分析方法；最后，以我國某核電廠廠址安全殼結構為算例，生成場地相關一致危險譜、條件均值譜、廣義條件均值譜和條件一致危險譜，基于上述我國場地相關譜，得到我國算例場地安全殼結構地震易損性與風險結果，比較不同場地相關譜定義對核電安全殼地震易損性與風險評估結果影響，為我國核電廠地震易損性與風險評估中場地相關譜選取提供應用參考。

1 中國場地概率地震危險性分析與分解

1.1 中國場地概率地震危險性分析

標量型概率地震危險性分析可得到指定場地標量型地震危險性曲線，但標量型地震危險性曲線無法考慮強度參數間相關性。鑒于上述標量型危險性分析不足，BAZZURRO 等[7-8]提出了向量型概率地震危險性分析理論，IERVOLINO 等[9]提出了條件型概率地震危險性分析方法。同時，由于我國場地特點，中國概率地震危險性分析需要考慮中國地震環境特點。本文首先總結了標量型中國概率地震危險性分析理論，然后，提出了向量型中國概率地震危險性分析、條件型中國概率地震危險性分析、標量型中國概率地震危險性分解和向量型中國概率地震危險性分解理論方法，為中國場地一致危險譜、條件均值譜、廣義條件均值譜和條件一致危險譜生成提供地震危險性分析和分解理論基礎。

1.1.1 標量型中國概率地震危險性分析

由于我國場地地震環境具有時空不均勻性等特點，與國外Cornell-McGuire 地震危險性分析方法相比，我國概率地震危險性分析方法具有如下特點：1)我國場地具有多級震源區劃分；2)由于地震動數據相對缺乏，我國地震動預測方程大多是基于“轉化法”得到，通常具有長短軸預測方程形式。

我國標量型概率地震危險性分析理論可表述如下。

震級mj地震發生概率可表示為：

式中：m0為最小震級；muz為最大震級；β=bln10，其中，b為G-R 公式系數； ?m為單位區間震級。

地震發生概率可表示為：

式中，ν0為地震統計區發生震級大于m0地震的年平均發生率。

震級mj地震在每個場地各點平均發生概率為：

式中：fi,mj為地震統計區空間分布不均勻性的空間分布函數；Ai為潛在震源區面積。

考慮中國場地地震發生時空不均勻性特點，標量型中國概率地震危險性分析可表示為：

式中：f(θ) 為 方向角的概率密度函數；P(Y≥y|mj,(x,y)ki,θ)為強度參數發生某強度大小的超越概率。

1.1.2 向量型中國概率地震危險性分析

在標量型概率地震危險性分析基礎上，向量型概率地震危險性分析考慮了強度參數間相關性，由于多個強度參數向量型危險性分析計算相對較為復雜，并且計算量較大，本文僅介紹雙參數的向量型地震危險性分析方法。在中國標量型概率地震危險性分析基礎上(式(4))，考慮譜加速度相關性，中國向量型(兩參數)概率地震危險性分析理論可表示為：

式中：νi為地震年平均發生率；fSa1,Sa2(x1,x2|m,r,θ)表示向量型強度參數聯合發生概率密度函數；fM,R,Θ(m,r,θ)為震級、距離和方向角聯合發生概率密度函數。

震級m、距離r和方向角θ 為條件，強度參數Sa1和Sa2的聯合發生概率密度函數為：

式中：fSa1(x1|m,r,θ)為強度參數Sa1發生的概率密度函數；fSa2|Sa1(x2|x1,m,r,θ)為以強度參數Sa1為條件，強度參數Sa2發生的概率密度函數。

以強度參數Sa1為條件的強度參數Sa2條件概率密度函數可表示為：

式中：mlnSa2|x1,m,r,θ為條件預測方程中位值；σlnSa2|x1,m,r,θ為條件預測方程標準差。

條件中位值和條件標準差可分別表示為：

強度參數Sa1和Sa2的聯合平均發生率為：

式中，MRDSa1(x1)為強度參數Sa1的平均發生率密度。

強度參數Sa1和Sa2的聯合平均發生超越概率為：

中國向量型地震危險性分析中的強度參數相關性需要適用于中國場地地震發生時空不均勻性特點，同時，中國地震動預測方程通常采用長短軸預測方程的形式，不同潛在震源區中方向角不同，所以除了震級和距離之外，還需要對方向角進行積分運算。對于適用于中國場址的譜型相關性模型，JI 等[20]運用中國地震動數據生成了適用于中國場地的譜加速度相關性模型。王曉磊[2]也給出了基于蒙特卡洛模擬方法的中國向量型危險性分析程序。

1.1.3 條件型中國概率地震危險性分析

條件型概率地震危險性分析考慮了強度參數間相關性，以某強度參數發生為條件，預測其它強度參數發生的超越概率。中國條件型概率地震危險性分析理論可表述如下。

條件概率密度函數可表示為：

式中：fSa2|Sa1(x2|x1,m,r,θ)為以強度參數Sa1為條件的強度參數Sa2發生概率密度函數；fM,R,Θ(m,r,θ|,x1)為震級、距離和方向角聯合發生概率密度函數。

以強度參數Sa1、震級、距離和方向角為條件的強度參數Sa2發生概率密度函數可表示為：

式中：mlnSa2|x1,m,r,θ為條件預測方程的預測中位值；σlnSa2|x1,m,r,θ為條件預測方程的預測標準差。

條件預測方程的中位值和標準差可分別表示為：

式中：mlnSa2|m,r,θ為強度參數Sa2預測方程的預測中位值；mlnSa1|m,r,θ為強度參數Sa1預測方程的預測中位值； σlnSa1|m,r,θ為強度參數Sa1預測方程的預測標準差； σlnSa2|m,r,θ為強度參數Sa2預測方程的預測標準差； ρ1,2為強度參數Sa1和Sa2相關性系數。

條件型危險性分析可表示為：

式中，fSa2|Sa1(u2)為條件概率密度函數。

同時，基于條件概率公式，條件型概率地震危險性分析可由向量型危險性分析與標量型危險性分析比值得到，可表示為：

式中：MRDSa1,Sa2(u1,u2)為強度參數Sa1和Sa2聯合發生的平均發生率密度；MRDSa1(u1)為強度參數Sa1發生的平均發生率密度。

1.2 中國場地概率地震危險性分解

地震危險性分解是表示不同范圍震級、距離等地震對地震危險性貢獻率，相應于標量型中國概率地震危險性分析和向量型中國概率地震危險性分析理論，得到的地震危險性分解理論，可稱為標量型和向量型中國概率地震危險性分解。基于標量型和向量型中國概率地震危險性分解結果得到的設定地震可分別用于條件均值譜和廣義條件均值譜的生成計算中。條件危險性分析相應的分解結果，與相同強度參數的向量型危險性分解結果一致，本文就不重復列出。

1.2.1 標量型中國概率地震危險性分解

中國場地標量型地震危險性分解可由單位區間震級、距離和方向角條件下標量型地震危險性與總的標量型地震危險性之比表示，總的標量型地震危險性可表示為：

式中：PSaTj>sj|m,r,θ為強度參數SaTj發生某強度大小的超越概率；fM,R,Θ(m,r,θ)為震級、距離和方向角聯合發生概率密度函數。

單位震級、單位距離和單位方向角條件下的標量型危險性可表示為：

式中：νi為地震年平均發生率；PSaTj>sj|m,r,θ為強度參數Sa(Tj)發生某強度大小的超越概率；fM,R,Θ(m,r,θ)為震級、距離和方向角聯合發生概率密度函數。

標量型地震危險性分解可表示為：

式中： λsj,x,y,z為單位震級、單位距離和單位方向角條件下標量型地震危險性； λsj為總的標量型地震危險性。

基于上述分解結果，可得到設定地震為：

式中：mx-1～mx為單位區間震級；ry-1～ry為單位區間距離； θz-1～θz為單位區間方向角。

由于我國地震動預測方程通常具有長短軸方向，為了生成條件均值譜的設定地震，我國標量型概率地震危險性分解通常包括方向角的分解結果。

1.2.2 向量型中國概率地震危險性分解

中國場地向量型地震危險性分解可由單位區間震級、距離和方向角條件下向量型地震危險性與總的向量型地震危險性之比表示，總的向量型地震危險性可表示為：

式中：fSa1,Sa2(x1,x2|m,r,θ)為強度參數Sa1和Sa2的聯合發生概率密度函數；fM,R,Θ(m,r,θ)為震級、距離和方向角聯合發生概率密度函數。

單位區間震級、距離和方向角條件下向量型地震危險性可表示為：

式中，MRDSa1,Sa2,x,y,z(u1,u2)為單位區間震級、距離和方向角條件下向量型地震聯合平均發生率密度。

兩個參數聯合發生條件下，向量型地震危險性分解可表示為：

式中： λSa1>x1,Sa2>x2,x,y,z為單位區間震級、距離和方向角條件下向量型地震危險性超越概率；λSa1>x1,Sa2>x2為總的向量型地震危險性超越概率。

基于上述分解結果，可得到設定地震為：

式中：mx-1～mx為單位震級區間；ry-1～ry為單位距離區間； θz-1～θz為單位方向角區間； λsj,x,y,z為單位震級、單位距離和單位方向角條件下，向量型危險性超越概率； λsj為總的向量型危險性超越概率。

同樣，由于我國地震動預測方程通常具有長短軸方向，為了生成廣義條件均值譜的設定地震，我國向量型地震危險性分解通常包括方向角的分解結果。

2 中國場地相關譜

場地相關譜是概率地震危險性分析與分解的副產品，同時，場地相關譜也是核電廠結構地震易損性與風險分析的地震輸入基礎。核工程領域較早運用的是一致危險譜，但一致危險譜較為保守；針對上述情況，BAKER[11]提出了考慮譜型相關性的條件均值譜，條件均值譜的條件周期只有一個，通常譜型較窄，分析結果可能不保守。KISHIDA[14]提出了多個條件周期的廣義條件譜。廣義條件譜主要基于向量型危險性分解結果生成，中國場地向量型危險性分解是中國廣義條件譜生成基礎。同時，基于中國條件型概率地震危險性分析，可得到場地條件一致危險譜。本節首先總結了中國場地一致危險譜理論，然后提出了中國場地條件均值譜生成方法，給出了中國場地廣義條件譜理論及生成步驟，最后，給出了中國場地條件一致危險譜生成原理和步驟。

2.1 一致危險譜理論及生成步驟

2.1.1 一致危險譜理論

一致危險譜是場地概率地震危險性分析或場地地震安全評估副產品之一，是早期核電廠廠址廣泛采用的場地相關譜。一致危險譜各個周期譜加速度相對應的危險性水平相同，通常由不同設定地震控制。

2.1.2 一致危險譜生成步驟

一致危險譜生成步驟如圖1 所示，可總結如下：

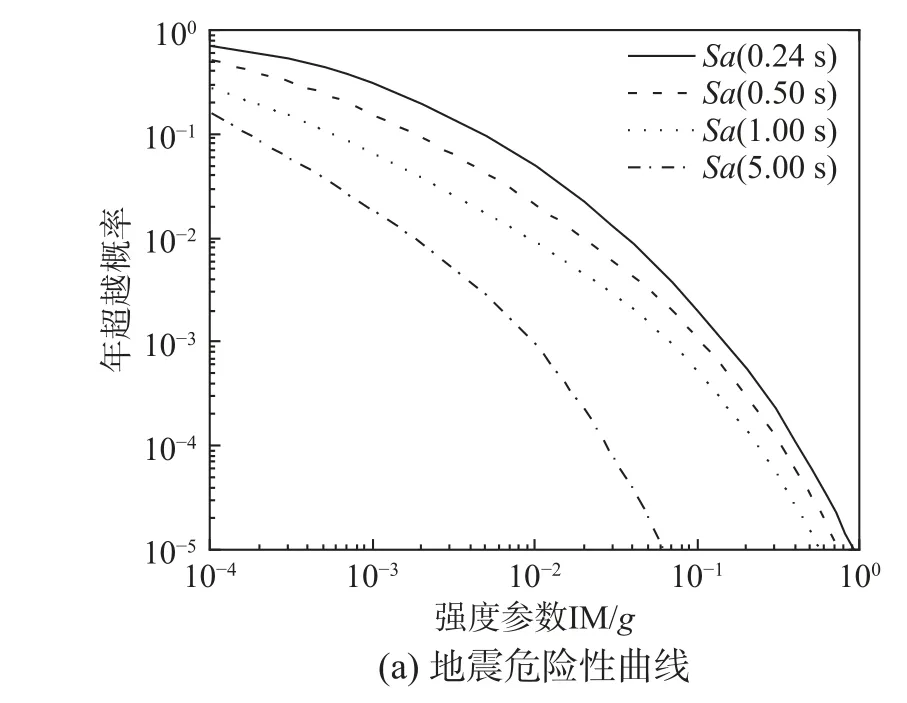
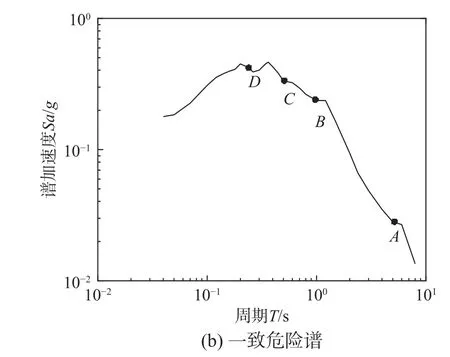
圖1 一致危險譜生成過程Fig.1 Generation process of uniform hazard spectra

1)基于場地危險性數據信息，進行場地概率地震危險性分析，生成場地地震危險性曲線；

2)根據核電廠結構、系統和部件設防地震等級，確定指定超越概率的譜加速度強度；

3)生成指定超越概率條件下的一致危險譜。

2.2 條件均值譜理論及生成步驟

2.2.1 條件均值譜理論

條件均值譜可表示為[11]：

式中：μlnS a(M,R,Ti) 和 σlnS a(Ti)分別為地震動預測方程中位值和標準差； ρ(Ti,T?)為譜型相關系數模型；ε (T?) 為周期T?譜加速度的譜型參數，可表示為：

式中： l nSa(T?) 為周期T?譜加速度在指定超越概率條件下的對數值；M和R為設定地震的震級和距離值。

2.2.2 條件均值譜生成步驟

中國場地條件均值譜生成步驟主要包括：

1)基于場地危險性數據，進行場地概率地震危險性分析與分解；

2)基于生成的地震危險性曲線和地震危險性分解結果，生成指定超越概率的條件譜加速度強度值和設定地震；

3)采用適用中國場地條件的譜加速度相關性模型；

4)基于上述信息，采用式(26)和式(27)生成場地條件均值譜。

2.3 廣義條件譜理論及生成步驟

2.3.1 廣義條件譜理論

KISHIDA[14]提出的多個條件強度參數的廣義條件譜可表示如下。

強度參數向量可表示為：

式中：Ac為條件強度參數；As為預測強度參數。

強度參數均值向量可表示為：

式中：μc為條件強度參數均值；μs為預測強度參數均值。

強度參數方程和協方差矩陣可表示為：

式中： Σcc為條件強度參數協方差矩陣； Σcs為條件強度參數和預測強度參數協方差矩陣； Σss為預測強度參數協方差矩陣。

條件參數均值向量可表示為：

式中： ε為譜型參數向量； σc為譜型參數方差。

條件參數協方差向量可表示為：

譜型參數向量與譜型參數方差乘積可表示為：

式中：ac為條件強度參數；μc為條件強度參數均值。

2.3.2 中國場地廣義條件譜理論與生成步驟

中國場地廣義條件譜生成原理與國際上已提出的廣義條件譜理論相同，但由于中國場地地震環境特點，在中國場地廣義條件譜生成計算中需要考慮中國場地地震環境特征和地震動預測方程特點，應考慮以下幾點：

1)基于中國場地地震環境特點，進行中國標量型概率地震危險性分析、向量型概率地震危險性分析以及向量型概率地震危險性分解運算；

2)基于中國標量型概率地震危險性分析結果，得到指定標量型超越概率強度參數大小，或基于中國標量型和中國向量型概率地震危險性分析，得到指定標量型和向量型超越概率強度參數大小；

3)在生成中國場地廣義條件譜時，需要生成適用于中國地震動預測方程求解的向量型設定地震，包括：震級、距離和方向角；

4)中國場地廣義條件譜需要考慮我國地震環境特點，采用適用于中國場地的譜加速度相關系數模型。

中國場地廣義條件均值譜可基于以下步驟生成：

1)基于場地危險性信息，進行中國場地標量型概率地震危險性分析；

2)基于場地危險性信息，進行中國場地向量型概率地震危險性分析與分解；

3)采用適用于中國場地的譜型相關性模型，基于中國廣義條件譜理論公式(式(31)和式(32))，利用中國標量型概率地震危險性分析、中國向量型概率地震危險性分析與分解結果，生成中國場地廣義條件譜。

2.4 條件一致危險譜理論及生成步驟

2.4.1 條件一致危險譜理論

條件一致危險譜是場地條件概率地震危險性分析副產品之一。條件一致危險譜是基于生成的條件地震危險性曲線，指定某一超越概率，確定條件一致危險譜。條件一致危險譜能夠考慮在指定強度參數發生條件下的具有一致超越概率的其它強度參數發生強度大小。

2.4.2 條件一致危險譜生成步驟

條件一致危險譜生成步驟如圖2 所示，可總結如下：

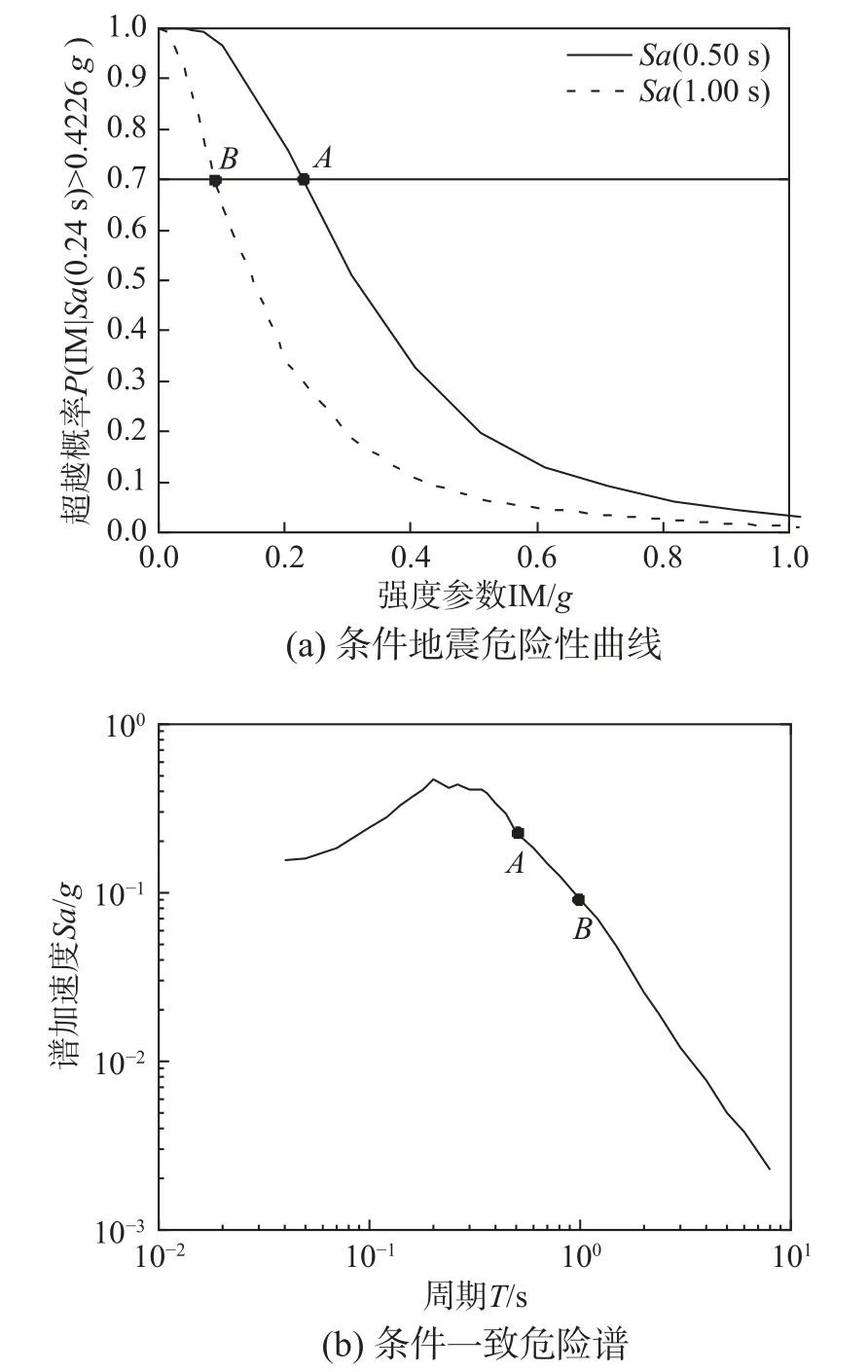
圖2 條件一致危險譜生成過程Fig.2 Generation process of conditional uniform hazard spectra

1)基于場地危險性數據信息，進行場地概率地震危險性分析，生成場地地震危險性曲線；

2)根據核電廠結構、系統和部件設防地震等級，確定譜加速度指定超越概率；

3)生成指定超越概率條件下的條件一致危險譜。

3 核電廠結構地震易損性與風險模型

3.1 核電廠地震易損性模型

3.1.1 核電廠平均值地震易損性模型

核電廠平均值地震易損性函數可表示為[21]：

式中：aC為中位值；βC為不確定性標準差，由表示知識不確定性標準差和本質不確定性標準差平方和開平方得到，即

3.1.2 考慮置信度核電廠地震易損性模型

考慮置信度的核電廠地震易損性函數可表示為[21]：

式中：aC為中位值；βU為考慮知識不確定性標準差；βR為考慮本質不確定性標準差；Q為置信度；Ф為標準正態累積分布函數；Ф-1為標準正態分布逆函數。

3.1.3 基于場地相關譜的地震易損性

在確定核電廠結構地震易損性函數時，可將場地相關譜選為地震輸入或地震動選取目標譜，進行核電廠結構振型分解反應譜法分析，或基于目標譜選取地震動記錄，然后進行核電廠結構時程分析，最后基于易損性分析統計方法，得到易損性函數變量。

3.2 核電廠結構地震風險解析模型

3.2.1 核電廠結構地震風險點估計解析模型

核電廠結構地震風險模型是地震危險性函數與地震易損性函數卷積積分，可表示為[22]：

式中：H(a)為地震危險性函數；FC(a)為地震易損性函數。

地震危險性函數可表示為[23]：

將式(34)和式(38)代入式(36)，得到地震風險解析函數，可表示為：

3.2.2 核電廠結構地震風險區間估計解析函數

考慮置信度的核電廠易損性函數(式(35))經過轉化，可表示為[21]：

式中，aC,Q為考慮置信度的中位值，可表示為：

將式(41)代入式(39)，可得到考慮置信度的地震風險解析函數，則考慮知識不確定性(易損性函數中的知識不確定性)的風險函數可表示為：

將式(38)代入式(42)，得到考慮知識不確定性的風險函數，可進一步表示為：

3.2.3 基于場地相關譜的地震風險

在確定核電廠結構地震風險函數時，可將場地相關譜選為地震輸入或地震動選取目標譜，直接進行核電廠結構振型分解反應譜法分析，或基于目標譜選取地震動記錄，進行核電廠結構時程分析，然后基于易損性分析統計方法，得到易損性函數變量，最后通過卷積計算或地震風險解析函數(式(39)和式(43))，得到地震風險結果。

4 算例分析

4.1 我國某核電廠址地震危險性信息

算例廠址信息如表1 和圖3 所示，包括一個地震統計區，地震統計區參數值如表1 所示，地震統計區范圍為東經109 度～116 度、北緯19 度～24 度，主要包含32 個潛在震源區，如圖3 所示。潛在震源區地震發生空間分布函數、最大震級和方向角及權重參見文獻[6]。

表1 地震統計區參數值Table 1 Parameters of seismic statistical zones

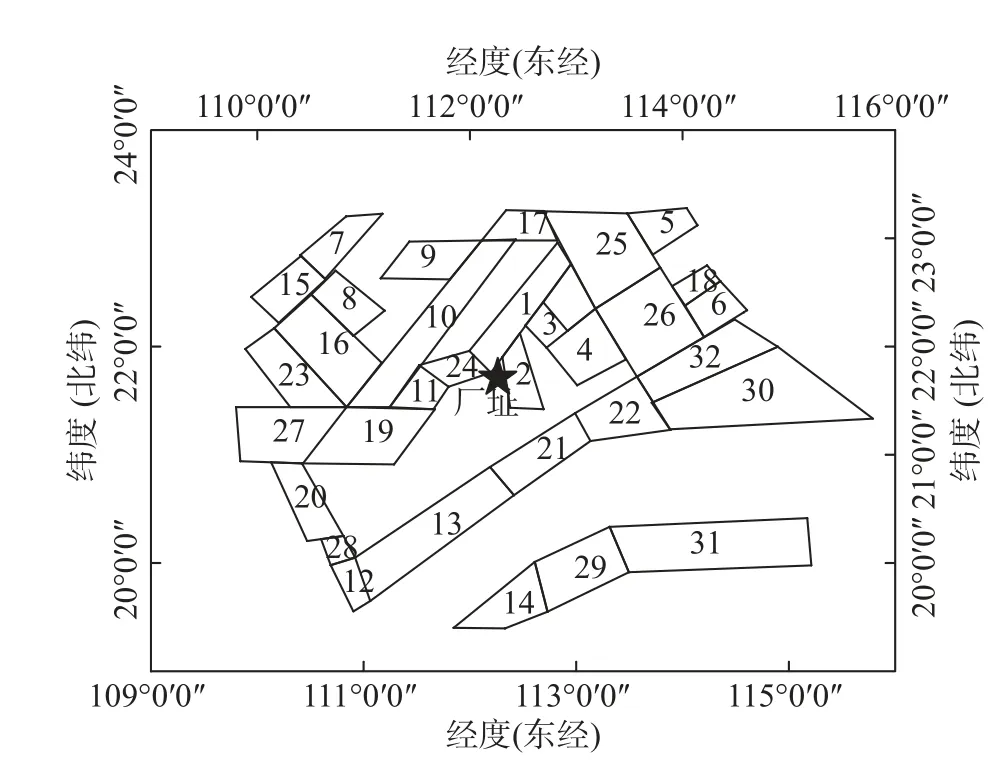
圖3 潛在震源區分布圖Fig.3 Distribution map of potential seismic source

本文采用霍俊榮[24]1989 年博士論文列出的我國華南地區地震動預測方程，可表示為：

式中：M為震級；R為距離；C1、C2、C3、C4和C5分別為預測方程系數，具體數值參見文獻[24]；σlog(Y)為不確定性標準差；ε 為譜型參數。

4.2 算例廠址概率地震危險性分析

4.2.1 算例廠址地震危險性曲線

基于算例廠址地震危險性信息，采用中國標量型概率地震危險性分析方法(式(4))，可得到指定強度參數的標量型地震危險性曲線，如圖4所示。

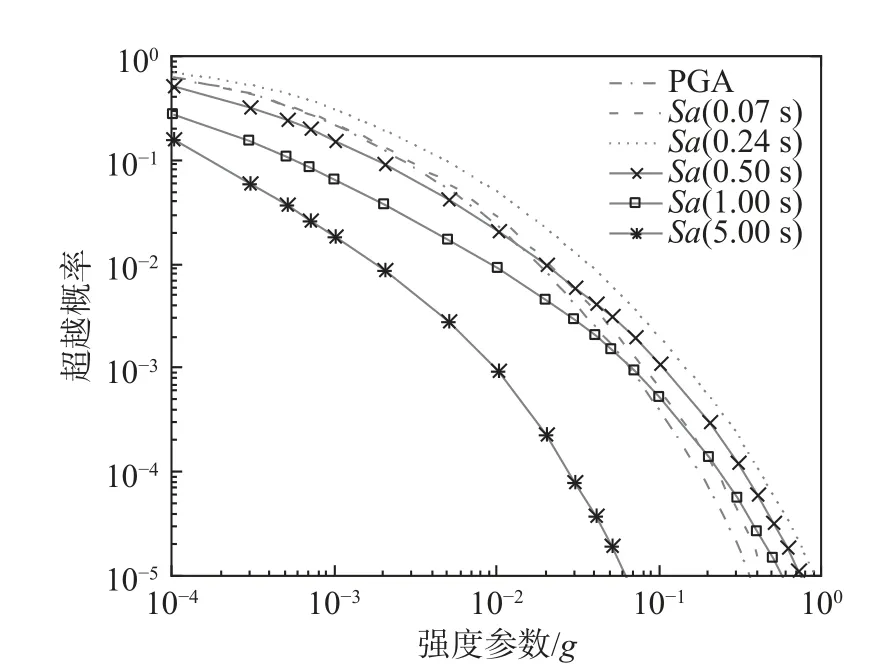
圖4 算例廠址地震危險性曲線Fig.4 Seismic hazard curve for the example site

4.2.2 算例廠址地震危險性曲面

基于算例廠址地震危險性信息，采用中國向量型概率地震危險性分析方法(式(11))，可得到向量型概率地震危險性曲面，如圖5 所示，可發現：相同強度大小的Sa(0.07 s)超越概率比Sa(0.24 s)的超越概率大；強度參數Sa(0.07 s)和強度參數Sa(0.24 s)的聯合危險性曲面上，固定相同強度參數Sa(0.24 s)大小的危險性曲線比固定相同強度參數Sa(0.07 s)大小的危險性曲線更陡。

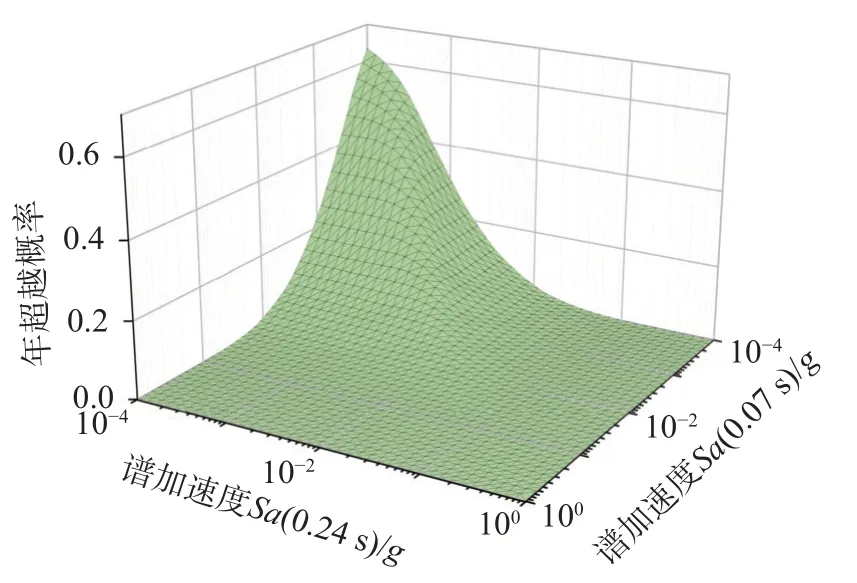
圖5 算例廠址地震危險性曲面Fig.5 Seismic hazard surface for the example site

4.2.3 算例廠址條件地震危險性曲線

基于算例廠址地震危險性信息，采用中國條件型概率地震危險性分析方法(式(16)或式(17))，可得到條件型概率地震危險性曲線，以強度參數Sa(0.24 s)為條件的強度參數Sa(0.07 s)的條件危險性曲線如圖6 所示。

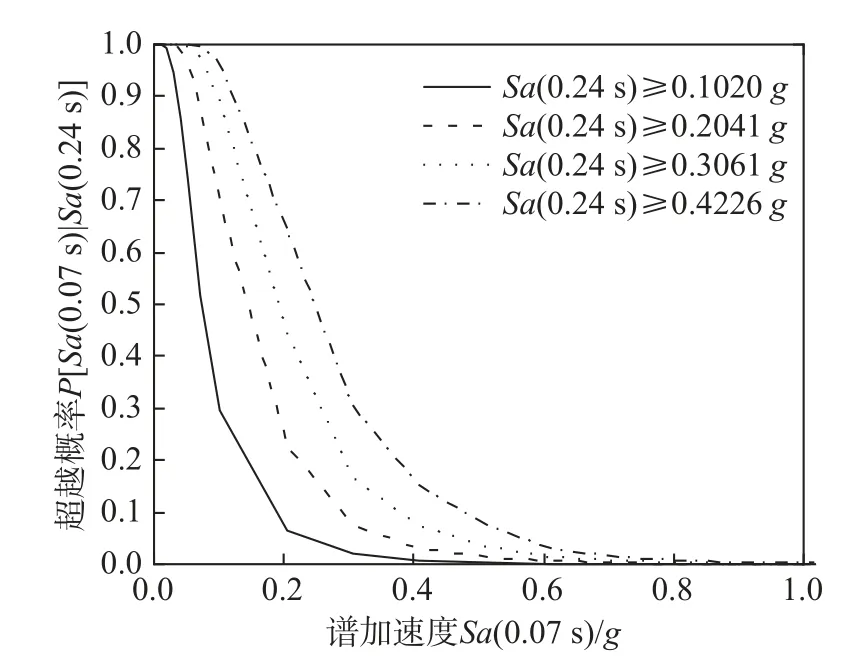
圖6Sa(0.07 s)條件危險性曲線Fig.6Sa(0.07 s) conditional hazard curves

4.3 算例廠址地震危險性分解

4.3.1 算例廠址標量型地震危險性分解

基于標量型地震危險性分解理論(式(20))，可得到算例廠址標量型地震危險性分解結果，強度參數Sa(0.24 s)和Sa(0.07 s)年超越概率分別為萬分之一的地震危險性分解結果如圖7 所示。基于標量型設定地震計算理論(式(21))，可得到算例廠址標量型設定地震，如表2 所示。

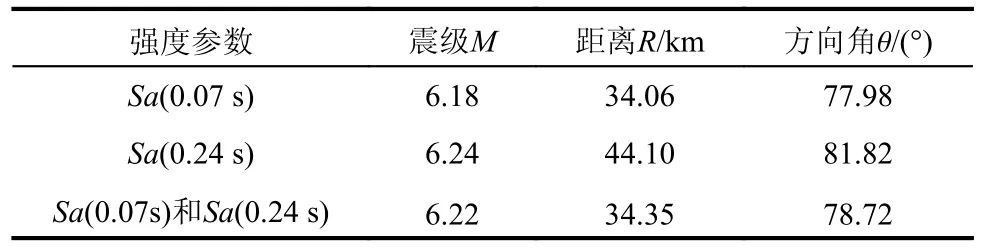
表2 設定地震Table 2 Scenario earthquake

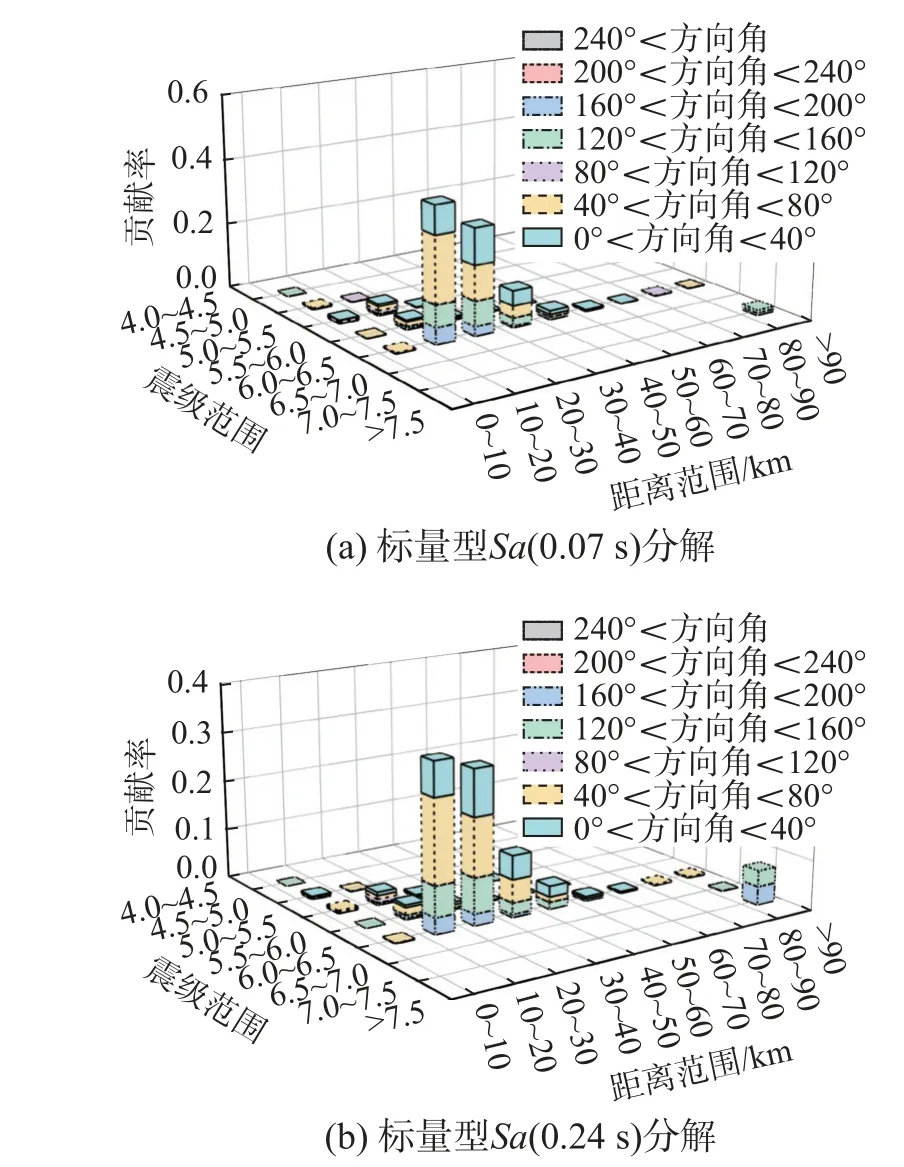
圖7 標量型地震危險性分解結果Fig.7 Scalar seismic hazard disaggregation results

4.3.2 算例廠址向量型地震危險性分解

基于向量型地震危險性分解理論(式(24))，可得到算例廠址向量型地震危險性分解結果，如圖8所示。基于向量型設定地震計算理論(式(25))，可得到強度參數Sa(0.24 s)和Sa(0.07 s)年超越聯合概率為萬分之一的向量型設定地震，如表2 所示。

圖8 向量型Sa(0.07 s)和Sa(0.24 s)分解結果Fig.8 Seismic hazard disaggregation results ofSa(0.07 s) andSa(0.24 s)

通過比較三個分解結果可發現：三個分解結果都不相同。同時為了利用分解結果生成適用于中國場地的條件均值譜和廣義條件均值譜的設定地震，基于式(21)和式(25)，分別計算了場地標量型和向量型設定地震，同樣發現三個設定地震不相同。

4.4 我國某核電廠場地相關譜生成

4.4.1 一致危險譜

基于生成的算例廠址地震危險性曲線，根據一致危險譜生成原理及步驟，得到算例廠址一致危險譜(Uniform hazard spectrum, UHS)，如圖9 所示。

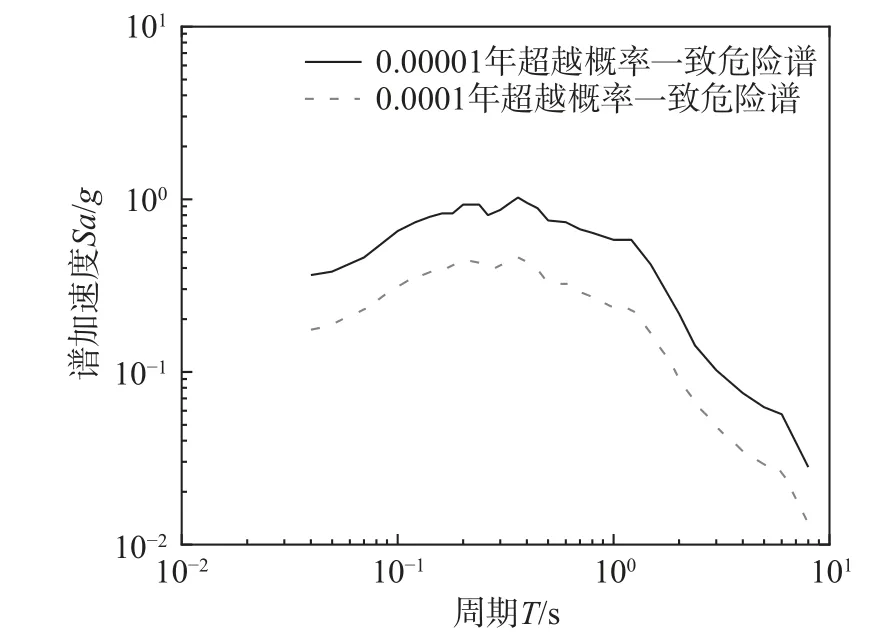
圖9 一致危險譜Fig.9 Uniform hazard spectra

4.4.2 條件均值譜

基于生成的算例廠址地震危險性曲線和設定地震，根據條件均值譜生成原理及步驟，分別選取Sa(0.07 s)和Sa(0.24 s)為條件強度參數，采用中國場地譜型相關性模型[20]，得到算例廠址條件均值譜(Conditional mean spectrum, CMS)，如圖10所示。

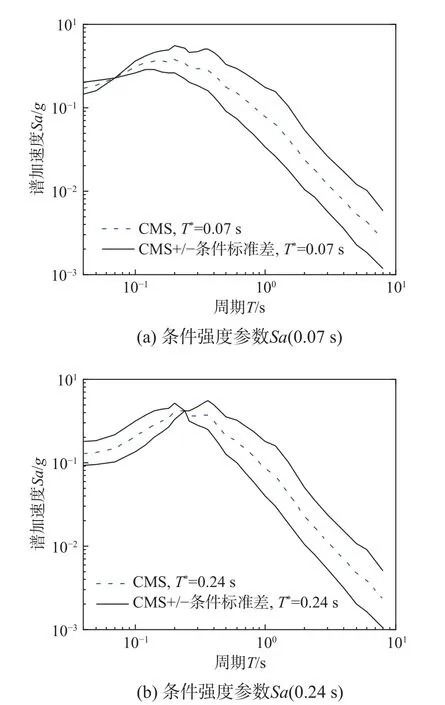
圖10 條件均值譜Fig.10 Conditional mean spectrum

4.4.3 廣義條件均值譜

基于生成的算例廠址地震危險性曲線、曲面和設定地震，根據廣義條件均值譜生成原理及步驟，采用中國場地譜型相關性模型[20]，選擇Sa(0.07 s)和Sa(0.24 s)為聯合條件強度參數，得到算例廠址廣義條件均值譜(Generalized conditional mean spectrum, GCMS)，如圖11 所示，可發現：兩個條件強度參數大小與一致危險譜一致，其它和一致危險譜不同，兩個條件強度參數的不確定性標準差為0，距離條件周期越遠，不確定性標準差越大。

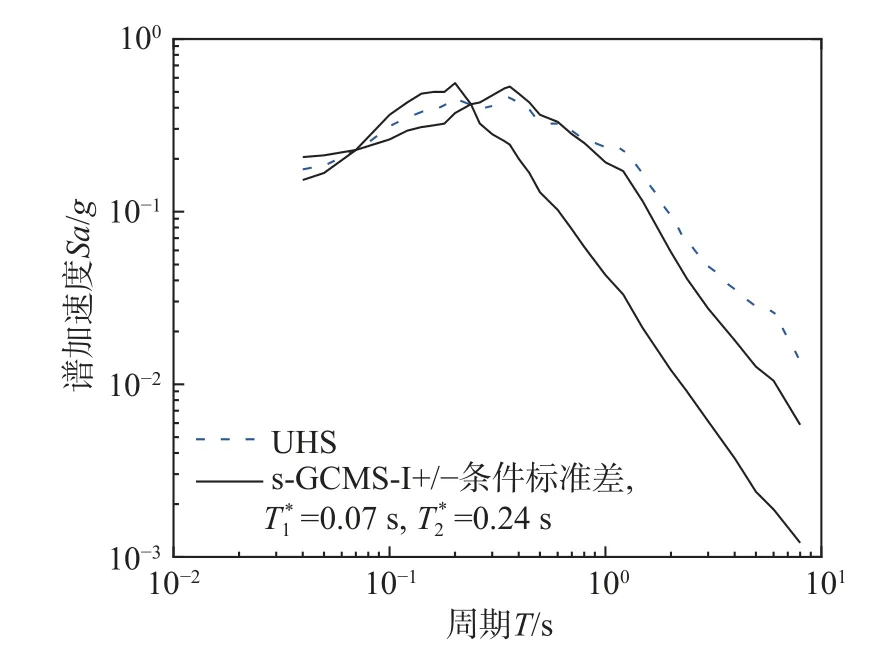
圖11 生成的廣義條件譜與一致危險譜Fig.11 Generalized conditional mean spectrum and uniform hazard spectrum

4.4.4 條件一致危險譜

基于生成的算例廠址條件地震危險性曲線，根據條件一致危險譜生成原理及步驟，生成了算例廠址條件一致危險譜(Conditional uniform hazard spectrum, CUHS)，如圖12 所示。

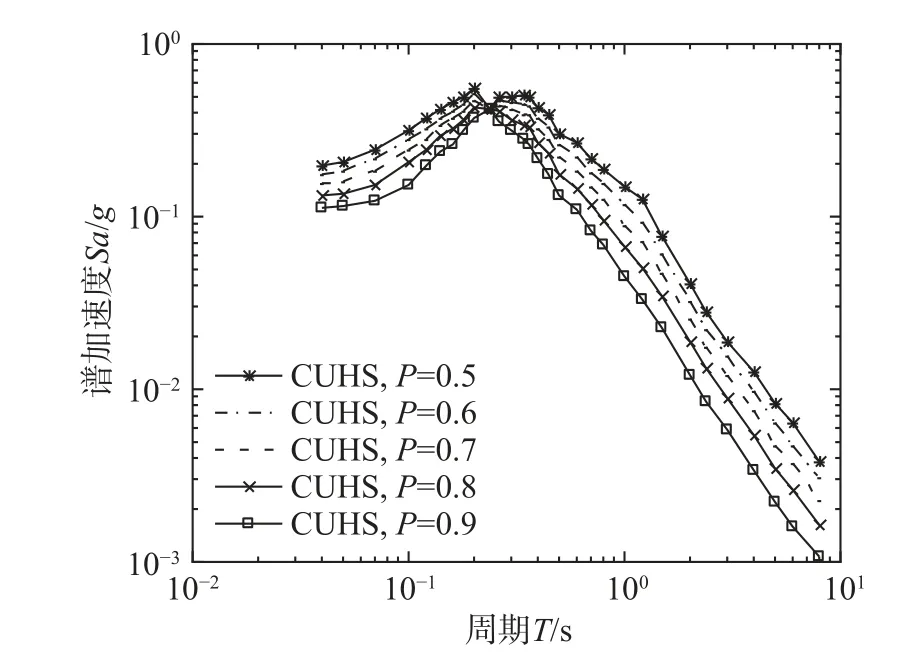
圖12 條件一致危險譜Fig.12 Conditional uniform hazard spectrum

4.4.5 比較分析

將算例廠址一致危險譜、條件均值譜、廣義條件均值譜和條件一致危險譜進行比較，如圖13所示。可發現：一致危險譜最為保守；廣義條件均值譜是指定周期條件譜的涵蓋譜；指定概率的條件一致危險譜譜型比一致危險譜窄、比條件均值譜譜型寬；條件均值譜相較于其它譜型更窄。

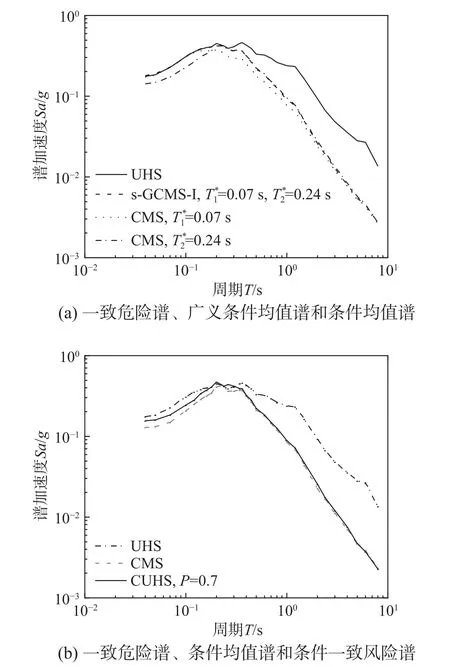
圖13 場地相關譜比較Fig.13 Comparison of site-specific spectra

4.5 算例廠址安全殼模型

4.5.1 算例廠址安全殼模型信息

本文以我國華南地區某核電廠安全殼為算例[25]，安全殼集中質量梁單元模型(如圖14 所示)節點和單元信息如表3 所示[25]，材料參數如表4 所示[25]。本文采用開源有限元程序OpenSees 進行建模，將安全殼混凝土和鋼材料貢獻按照簡化后單元力學性能綜合考慮，將安全殼簡化后的梁單元采用Timoshenko 梁單元模擬(可模擬單元的剪切變形)，力學性能如表3 所示。該安全殼模型模態分析結果如表5 所示，模態1、模態2 和模態5 分別為安全殼前三階平動模態周期。

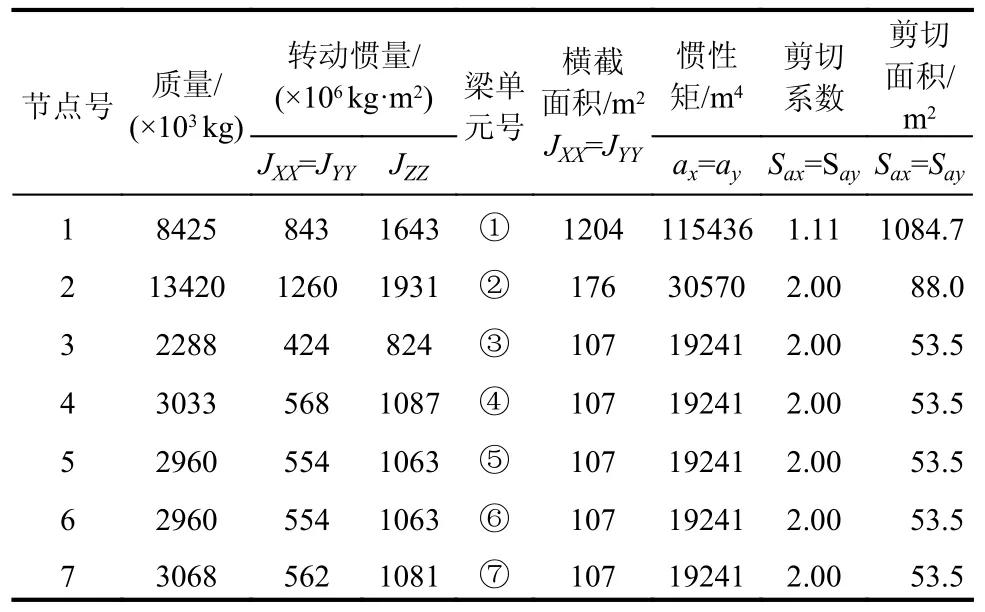
表3 安全殼和筏板基礎集中質量梁單元模型節點和單元[25]Table 3 Nodes and elements of lumped mass beam element model of the containment and raft foundation[25]

表4 材料參數[25]Table 4 Material parameters[25]

表5 模態分析結果Table 5 Results of modal results

圖14 安全殼集中質量梁單元模型Fig.14 Lumped mass beam element model of containment

4.5.2 安全殼模型極限狀態定義

安全殼是核電廠最后一道防線，在極端災害作用下，其完整性能力可有效保障放射性物質的泄露，所以通常假設安全殼在災害作用下，達到塑性狀態時，安全殼達到失效狀態。安全殼結構可由三線性骨架曲線[26]表示(如圖15 所示)，假設當安全殼剪應力達到第一條線拐點時，安全殼達到塑性狀態，即安全殼失效。第一個拐點剪切應力可表示為[26]：

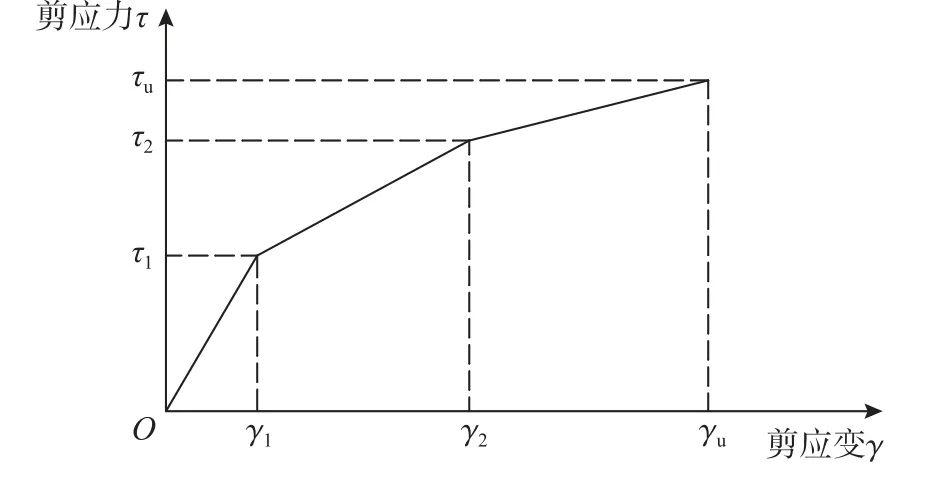
圖15 骨架曲線Fig.15 Skeleton curve

式中：FC為混凝土抗壓強度；σV為豎向壓應力。

4.6 算例廠址安全殼地震易損性

4.6.1 核電廠結構地震易損性分析步驟

本文基于核電廠安全殼地震易損性安全系數法[27-28]，采用以下分析步驟：

1)基于場地危險性信息，生成廠址場地相關譜；

2)建立安全殼有限元模型；

3)基于振型分解反應譜法，得到不同場地相關譜作用下，安全殼結構的地震響應，得到易損性函數中強度系數的中位值；

4)基于解析和經驗數據(安全系數法中除了強度系數中位值以外的其它安全系數取經驗數值)相結合方法，確定安全系數的中位值和標準差；

5)基于安全系數法，確定不同場地相關譜作用下的安全殼結構地震易損性曲線。

4.6.2 算例廠址核電廠安全殼地震易損性結果

采用本文4.6.1 節易損性分析步驟(經驗數據采用表6 中數據范圍的中位值)，基于不同場地相關譜，可計算安全殼地震易損性曲線，如圖16 和圖17 所示。計算得到核電廠安全殼高置信度低失效概率值(High confidence of low probability of failure, HCLPF)[2]，如表7 所示，可發現：以平動第1 周期和第2 周期(前兩階平動周期相同)的譜加速度Sa(0.24 s)為強度參數計算得到的HCLPF值大于以平動第3 周期加速度Sa(0.07 s)為強度參數計算得到的HCLPF 值；相較于UHS、GCMS和CUHS，基于CMS 計算的HCLPF 值較大，即基于CMS 得到HCLPF 值偏于不保守，用于篩選核電廠結構的抗震能力，可能偏于不安全。

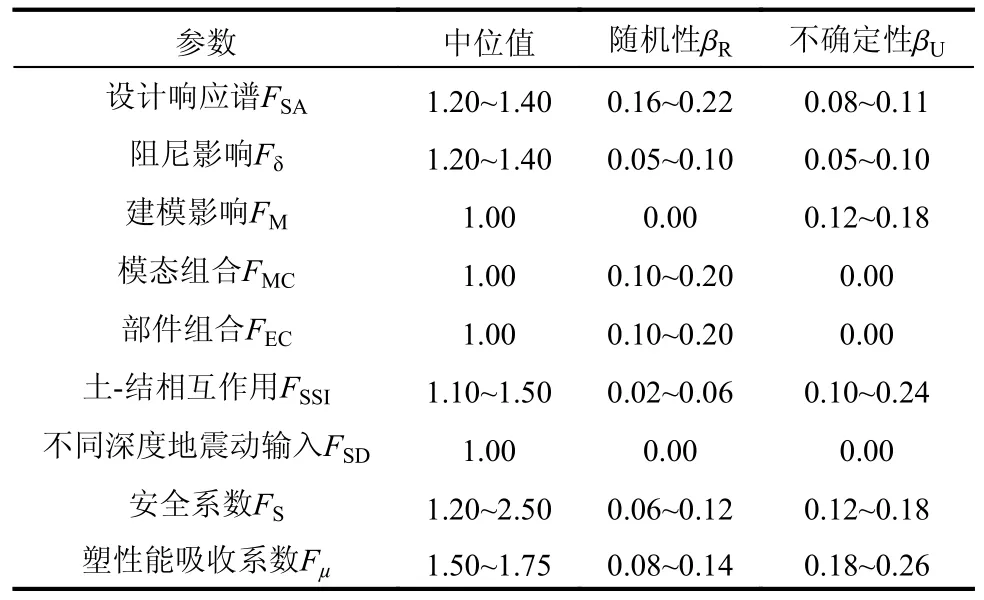
表6 經驗地震易損性數據[27-28]Table 6 Empirial seismic fragility data[27-28]

表7 安全殼HCLPF 值Table 7 HCLPF values of containments

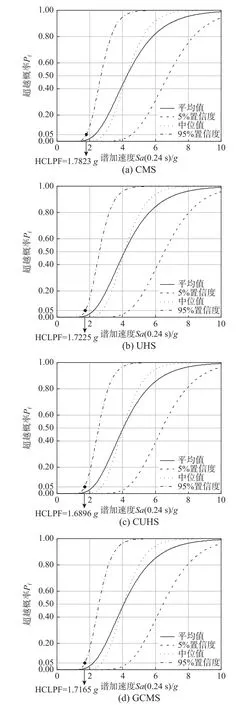
圖16 以Sa(0.24 s)為強度參數值的安全殼地震易損性曲線和高置信低失效概率值Fig.16 Seismic fragility curves and HCLPF values of a containment takingSa(0.24 s) as intensity measure

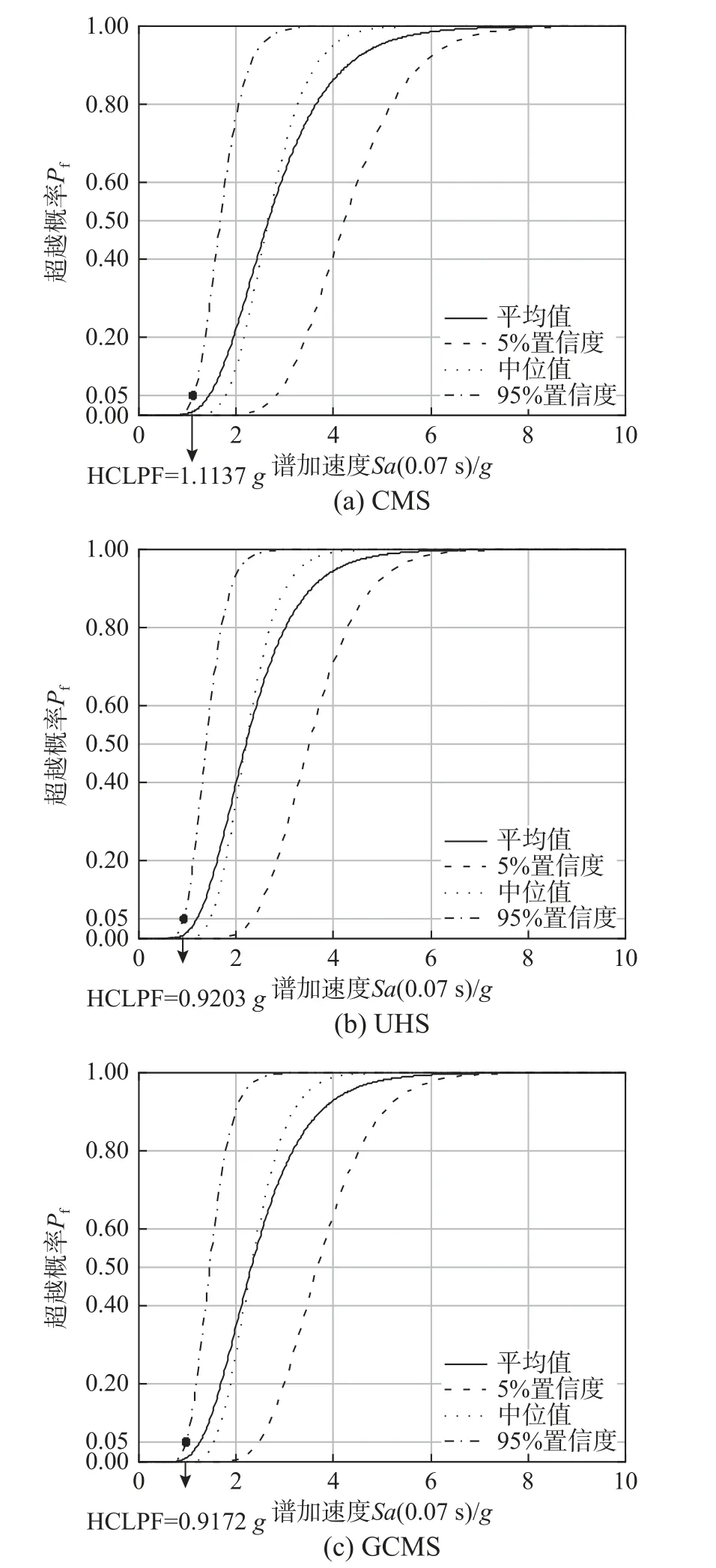
圖17 以Sa(0.07 s)為強度參數值的安全殼地震易損性曲線和高置信低失效概率值Fig.17 Seismic fragility curves and HCLPF values of a containment takingSa(0.07 s) as intensity measure

4.7 算例廠址安全殼地震風險

4.7.1 地震危險性解析函數

基于地震危險性解析函數(式(38))，可得到Sa(0.07 s)和Sa(0.24 s)危險性曲線參數，如表8 所示。

表8 地震危險性參數Table 8 Seismic hazard parameters

4.7.2 算例廠址安全殼解析地震風險

基于地震風險解析函數(式(39)或式(43))，可得到該核電廠安全殼地震風險點估計和區間估計結果，如表9 和表10 所示，可發現：以平動第一周期的譜加速度Sa(0.24 s)為強度參數計算得到的地震風險大于以平動第三周期加速度Sa(0.07 s)為強度參數計算得到的地震風險；相較于UHS、GCMS 和CUHS，基于CMS 計算的地震風險較小，即基于CMS 得到的地震風險偏于不保守；基于各類場地相關譜得到的安全殼地震風險都較大。

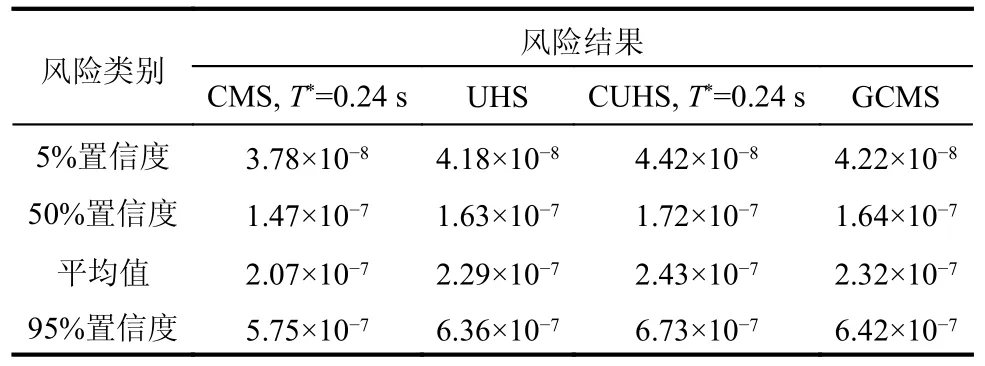
表9 以Sa(0.24 s)為強度參數的某安全殼地震風險結果Table 9 Seismic risk results of a containment usingSa(0.24 s) as intensity measure

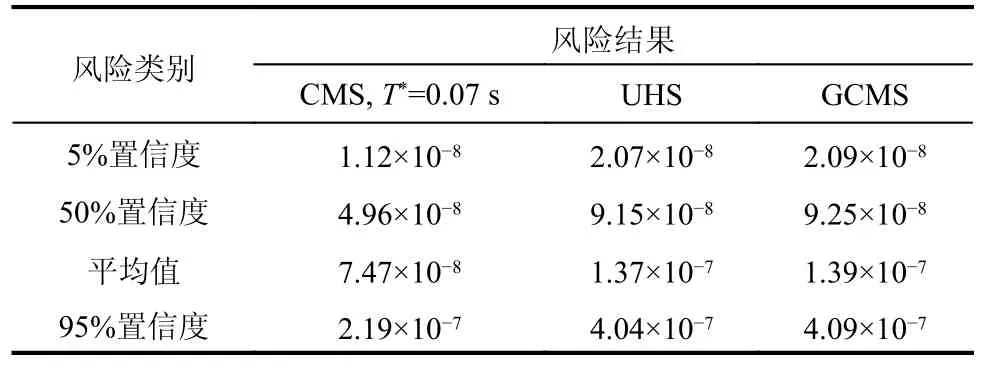
表10 以Sa(0.07 s)為強度參數的某安全殼地震風險結果Table 10 Seismic risk results of a containment usingSa(0.07 s) as intensity measure

5 結論

本文首先總結了中國標量型地震危險性分析、中國向量型地震危險性分析、中國條件型地震危險性分析、中國標量型地震危險性分解和中國向量型地震危險性分解理論方法，總結了中國場地一致危險譜基本原理，分別提出了中國場地條件均值譜、廣義條件均值譜和條件一致危險譜理論，給出了核電廠結構地震易損性和風險分析理論，以我國某核電廠廠址安全殼結構為應用算例，分別生成了算例廠址地震危險性曲線、地震危險性曲面、條件地震危險性曲線，并計算了算例廠址標量型和向量型地震危險性分解結果，基于上述計算結果，得到了算例廠址UHS、CMS、GCMS 和CUHS，針對算例廠址安全殼，得到了算例場地安全殼結構地震易損性與風險評估結果。基于上述研究，得到以下結論：

(1)中國標量型和向量型地震危險性分解是中國場地條件均值譜和廣義條件譜生成基礎；

(2)基于條件危險性分析可生成條件一致危險譜；

(3)相較于UHS、GCMS 和CUHS，基于CMS計算的安全殼HCLPF 值較大，即基于CMS 得到的HCLPF 值偏于不保守；

(4)相較于UHS、GCMS 和CUHS，CMS 計算得到的安全殼地震風險結果較小，即選用CMS為場地相關譜計算得到的風險結果偏于不保守；

(5)不同場地相關譜條件下，我國核電廠安全殼模型安全裕量都較大。