融合改進Dijkstra算法和動態窗口法的移動機器人路徑規劃*
郭 建,楊 朋,曾志豪,黃穎駒,王家淳
(廣州城市理工學院機械工程學院,廣州 510800)
0 引言
移動機器人(AGV)路徑規劃可以幫助機器人更好的服務于智能制造、智慧工廠等高自動化場景下的物流運輸,具有廣泛的應用前景[1]。
路徑規劃可分為基于先驗信息的全局路徑規劃和基于傳感器信息的局部路徑規劃[2],其中全局路徑規劃有:RRT算法[3]、A*算法[4]、遺傳算法(GA)[5]、Dijkstra算法[6]。局部路徑規劃則包含:人工勢場法(APF)[7]、D*算法[8]、DWA算法[9]、蟻群算法和強化學習法等。
Dijkstra算法在搜索最優路徑時,需要對地圖環境進行幾何劃分,從起點開始向周圍所有節點搜索,直至搜索到目標點為止,所尋路徑一定是最優的,但在搜索路徑時需要擴展許多無用的節點。且路徑軌跡存在折線,不夠平滑。馬新國等[9]提出一種融合改RRT和Dijkstra算法,利用改進的RRT算法獲得可行路徑并進行柵格化,在柵格化后的可行路徑上采用Dijkstra算法搜索最短路徑。提高機器人動態路徑規劃效率。但忽視機器人對軌跡光滑程度的要求。鞏慧等[10]采用基于幾何拓撲學方法對Dijkstra算法規劃的路徑進行平滑處理,有效減少了機器人轉彎次數,提高軌跡平滑度,但僅在靜態障礙物的條件下進行實驗驗證。局部路徑規劃中傳統DWA算法前瞻性不足[11-12],遇到“C”型障礙物時無法避障,也非最優路徑。卞永明等[13]提出一種改進DWA算法,增加計算仿真軌跡與關鍵航跡點的最小距離的評價函數,實現了安全性提升和路徑優化。王彬等[14]在DWA算法中改進障礙物距離評價子函數,提出了動態窗口法的自適應環境改進策略,使路徑更加平滑,但舍棄了可用速度的選擇,導致效率降低。
因此本文針對Dijkstra算法路徑轉折多,全局規劃效率低,DWA算法無法進行全局規劃問題,本文提出一種融合改進的Dijkstra算法和改進的DWA算法,解決動、靜態障礙物的場景下移動機器人的路徑規劃問題。仿真實驗以及移動機器人樣機實驗結果表明,本文研究的融合算法能夠提高移動機器人全局規劃效率以及避障能力。
1 移動機器人設計與建模
1.1 移動機器人運動學模型
移動機器人底盤采用差分驅動結構,由2個主動輪和4個從動輪組成,如圖1所示。
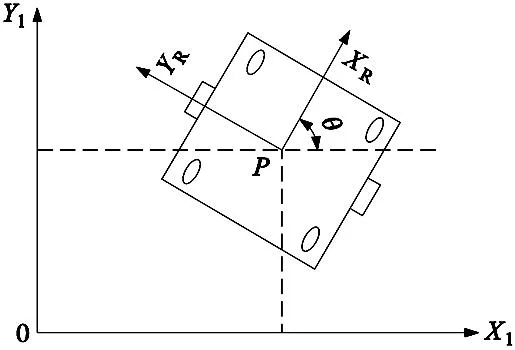
圖1 差分驅動移動機器人
圖1中,OX1Y1為全局坐標系,PXRYR為移動機器人坐標系,θ為機器人相對于全局坐標系偏轉角。設時間間隔Δt,移動機器人做勻速直線運動,t+1時刻,由機器人的線速度和角速度v、ω,可得:
(1)
式中:xt、yt、θt為t時刻下的位姿,θt為運動方向和水平方向的夾角。
1.2 移動機器人硬件
基于4 GB的64位Ununtu16.04操作系統,通過局域網實現上位機系統和機器人樣機的通訊,實現遠程操控移動機器人進行自主避障和導航功能。移動機器人樣機如圖2所示。

圖2 移動機器人樣機
采用興頌LE-50621-V1激光雷達掃描和獲取環境信息。使用步科FD124S-CA-000行走輪提供動力,外殼為3D打印材料ABS,移動機器人參數如表1所示。

表1 移動機器人參數
移動機器人運動參數如表2所示。

表2 機器人自身參數
2 Dijkstra算法改進及仿真
2.1 Dijkstra算法
Dijkstra算法屬于廣度優先搜索算法解決賦權有向圖或者無向圖的單源最短路徑問題,算法最終可以得到一個最短路徑樹,如圖3所示。
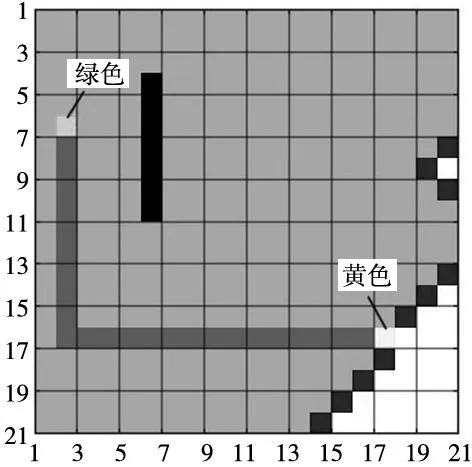
圖3 Dijkstra算法路徑導航
圖3中綠色為起點,黃色為終點,黑色物塊表示障礙物,淺灰色表示搜索路徑時經過的節點,深灰色區域表示搜索到最優的軌跡。
2.2 改進的Dijkstra算法
傳統Dijkstra算法以指定頻率運行,生成從當前位置到目標位置的一條安全路線。雖能完成避障,但在機器人繞過障礙物后,以當前位置重新規劃到目標點的路線,這種方式忽略了初始路徑的全局最優的特點。
改進路徑規劃始終保留以初始位置為起點的全局路徑規劃,并以局部優化的方式代替重新生成全局路線的原方案。步驟為:
步驟1:根據靜態全局代價地圖——不包含實時障礙物信息,生成初始路線;
步驟2:以指定頻率,根據動態的局部代價地圖優化初始路線。當存在與障礙物碰撞的子路徑段,使用Dijkstra算法重新計算的安全路徑替換,得到優化后路線,即只對部分路徑進行重新規劃,其余采用初始路徑;
步驟3:對于局部代價地圖內存在多個障礙物的情況,將多障礙物視為同一障礙物,一并繞開,以縮短小車繞障用時、提高效率。改進前后的路徑規劃效果對比如圖4所示。
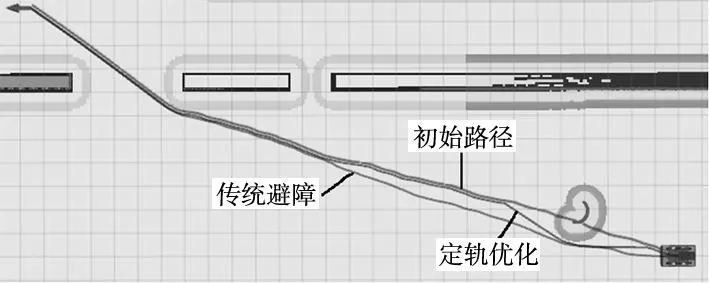
圖4 傳統路徑規劃與改進路徑規劃效果示意圖
2.3 路徑平滑
由于障礙物和局部軌跡優化,全局路徑存在轉折、不平滑的情況,不利于移動機器人平穩運動,故需對路徑進行平滑優化處理。
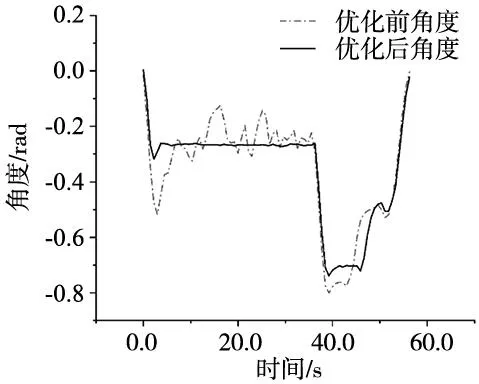
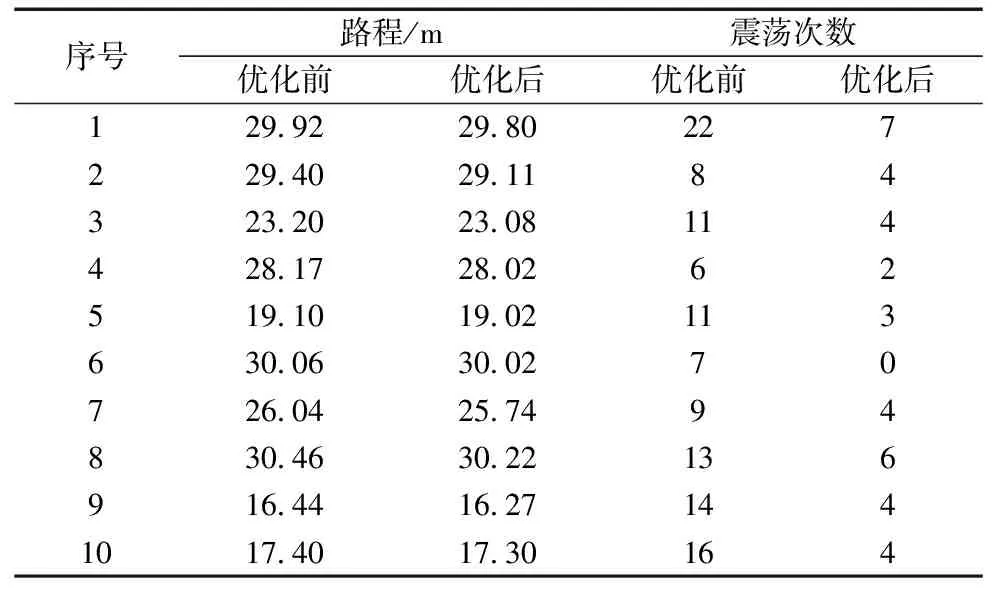
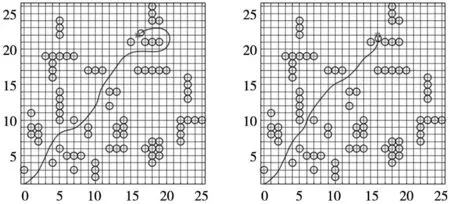
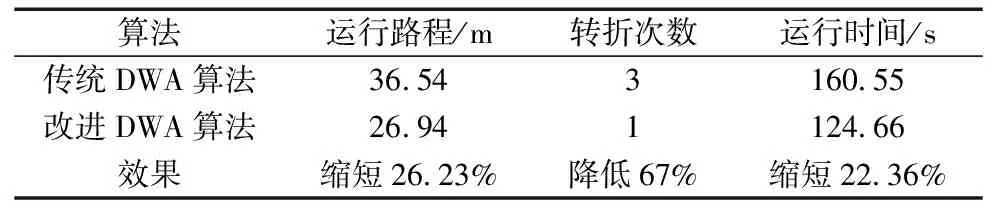
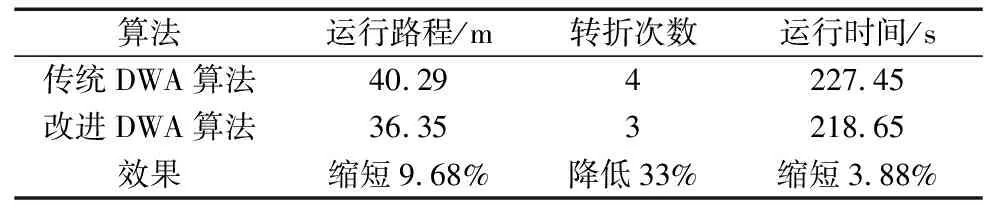
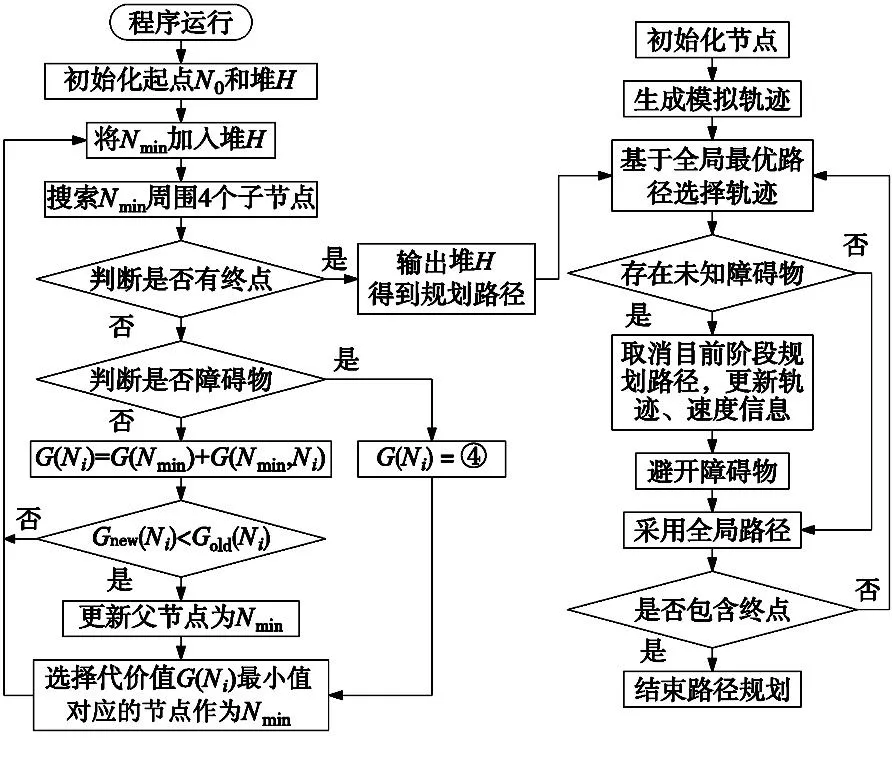
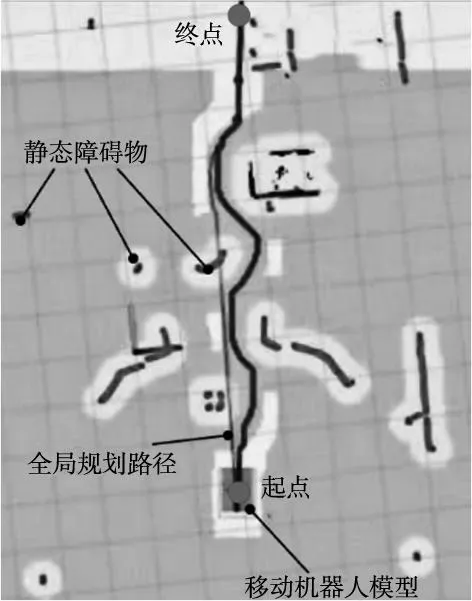
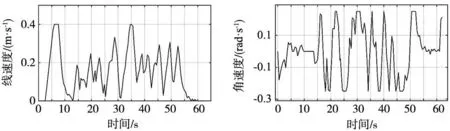
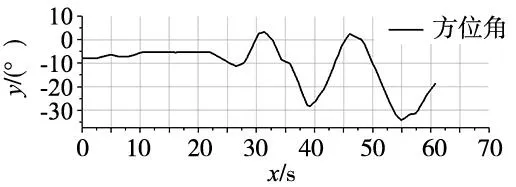
路徑優化可采用兩種優化方案,一種方案為直接刪除兩個路徑點間無障礙物碰撞的路徑點;但剔除點過多時,將導致小車對既定軌跡的貼合性降低。第二種方案為采用平滑過渡法對路徑點進行替換。本文采用第二種方法。對于某條在兩個路徑點之間無障礙物碰撞的子路徑,起始點為N0,終點為Nsn,過渡點為Nsi(0 (2) 對上述傳統規劃所得全局路徑進行路徑拉直優化處理后,得到平滑路徑如圖5所示。 圖5 路徑優化效果圖 全局路徑規劃采用相同的起點與終點,記錄下移動機器人在算法改進前后下,行進中的實際姿態角變化情況,如圖6所示,可以對比出算法規劃的安全路徑在優化前后的平滑性。 圖6 機器人實際姿態角變化圖 從圖6可以發現,在執行路徑優化后,得到的全局路徑中的姿態角震蕩次數由29次減少至7次,有顯著地降低。優化前姿態角的標準偏差為4.33°。優化后姿態角的標準偏差為0.26°。 通過對比優化前后的數據,可以發現機器人姿態角震蕩次數顯著降低(7<29),以及小車前進過程中的姿態角標準差(0.26°<4.33°)。可證明通過算法優化后,機器人左右擺動的情況得到明顯改善,且在機器人實際行進過程中,其機身姿態更為平穩,工作路徑得到有效縮短。 多組數據對比:再次隨機選取10組坐標,如表3所示,通過多次隨機實驗,避免數據的偶然性。分別采用傳統算法與優化算法進行路徑規劃,對比其優化前后的路程長度及偏航角震蕩次數如表4所示。 表3 隨機選取坐標組 表4 路程及震蕩次數對比 通過對比算法優化前后的多組數據,計算通過路徑平滑優化后,機器人的平均路程縮短比例為0.65%,平均偏航角震蕩次數減少了67.70%,證明路徑規劃算法改進后,路徑長度縮短,且更為平滑。 動態窗口算法(DWA)是一種常用的局部避障規劃算法。移動機器人在擁有完整環境信息的全局地圖下進行導航時,面對突然出現的障礙物,全局路徑規劃無法處理該問題,因此需要采用實時局部避障,DWA算法避開在速度搜索空間中可能與障礙物發生碰撞的路徑,對預測時間內的移動機器人速度空間采樣后,預測軌跡,并利用DWA算法中的評價函數選出最優軌跡。其評價函數為: E(v,ω)={σ(αhead(v,ω)+βdist(v,ω)+γvel(v,ω))} (3) 式中:head(v,ω)為當前速度下,評估目標方向與模擬的軌跡末端偏差;σ為平滑函數,α、β、γ為加權系數,vel(v,ω)為機器人當前運動速度大小的評價。 傳統DWA算法常常因為速度與偏差角變化的固定參數使得路徑安全性降低,其速度評價函數的權重總是小于其他評價子函數的權重,即算法中速度無法保證快速平穩到達終點,就會導致該軌跡不是最優解。除此之外,如果目標點突然出現障礙物,在機器人即將抵達目標點時,會出現運動十分緩慢甚至卡頓現象的情況。因此需要動態改變權重來解決此類問題。本文依靠障礙物的遠近動態改變速度評價權重大小,離障礙物越遠,越平緩接近終點,離障礙物越近,能夠快速避開障礙物。改進評價函數如式(4)所示。 E(v,ω)={σ(αhead(v,ω)+βdist(v,ω)+εDvel(v,ω))} (4) 式中: (5) 根據障礙物遠近動態調節vel(v,ω)的權重值εD,在仿真狀態下,設定障礙物半徑R=0.5 m,根據障礙物距離設定a=0.4,b=0.1,則εD范圍為(0.1~0.4)。 基于MATLAB對比相同地圖環境下改進前后的DWA算法仿真,起點為(0,0),如圖7所示。 (a) 傳統DWA算法 (b) 改進后DWA算法 結合圖7和表5可得,針對局部路徑規劃,相對于傳統DWA算法,改進的DWA算法運行路程縮短26.23%,路徑轉折次數降低了67%,運行時間減少22.36%。 表5 算法仿真對比 結合圖8和表6可得,相較于傳統的DWA算法,35×35 m柵格地圖環境內,改進后的DWA算法運行路程縮小9.68%,路徑轉折次數降低了33%,運行時間縮短3.88%。改進的DWA算法節約用時,提高了避障效率,并且使得軌跡轉折次數降低,機器人運動更加穩定。 表6 算法仿真對比 (a) 傳統DWA算法 (b) 改進后DWA算法 在全局規劃方面,利用改進的Dijkstra算法調整評價函數,減少冗余節點、縮短時間,提高搜索效率。在局部規劃方面,利用改進的DWA算法,依據移動機器人距離障礙物的遠近繞開障礙物,融合算法路徑規劃流程,如圖9所示。 圖9 融合算法路徑規劃流程圖 分別記錄融合算法對移動機器人面對靜態障礙物以及動態障礙物時軌跡規劃。其中,靜態障礙物場景下,移動機器人軌跡如圖10所示。 圖10 融合算法靜態避障路徑仿真 圖10中,黑色曲線為實時的路徑規劃,黑色直線為起點到終點的直線距離。灰色線為障礙物。在初始全局路徑規劃下,隨著障礙物的增多,路線也隨之變化。動態障礙物場景下,移動機器人路徑規劃如圖11所示。 (a) 避障初始路線 (b) 避障行駛路線 圖11中序號①~③均為靜態障礙物,機器人模型從起點出發,駛向終點,靠近動態障礙物時,重新規劃路徑,繞過動態障礙物。實驗仿真表明,無論是靜態還是動態障礙物,機器人依靠融合算法可以平滑且安全抵達目的地。 采用移動機器人樣機在真實環境下,驗證融合算法的有效性。如圖12所示。 圖12 移動機器人樣機實驗 圖12中①~⑦為靜態障礙物,移動機器人從起點出發首先規劃全局路徑,當受到全局路徑存在障礙物時,及時規劃局部避障路線,依次繞過障礙物抵達終點。面對真實的環境,能夠快速規劃出有效的避障路徑,驗證了融合算法的有效性。 記錄該過程中,移動機器人的線速度、角速度以及方位角,如圖13~圖15所示。 圖13 移動機器人線速度 圖15 移動機器人方位角 移動機器人線速度速度平緩上升至遇到障礙物,線速度由0.45 m/s平緩降低并不斷調整。角速度的變化波動明顯,證明融合算法實時調整避障路線,保證移動機器人路徑安全。移動機器人方位角變化平緩,不存在突變,證明融合算法規劃的路線變化平穩,符合移動機器人應用要求。 測得移動機器人在起始點A和終點B的重復定位精度,重復16次實驗,以第一次機器人坐標為參考,計算在A、B點機器人重復定位精度,如圖16和圖17所示。 圖16 A點重復定位精度 從圖16和圖17可知,移動機器人在A、B點的X方向平均誤差≤30 mm,在A、B點的Y方向平均誤差≤30 mm。證明該融合算法規劃的移動機器人運動具有良好定位精度。 綜上所述,改進Dijkstra算法和改進DWA算法的融合很好地規劃移動機器人全局路徑與局部路徑,具有實時避障能力,保證機器人移動過程中的效率和精確度。 本文提出一種基于傳統Dijkstra算法和DWA算法進行改進和融合的導航算法。滿足移動機器人運全局路徑規劃和動態避障。 (1)全局路徑規劃基于Dijkstra算法實現了平滑優化的路徑規劃以及動態避障功能。在實驗中,經過優化后路徑中采用的姿態角的標準偏差從4.33°降到0.26°,震蕩次數從29次降到7次;多次實驗,路程平均縮短0.65%,震蕩次數平均減少67.70%,故路徑得到了明顯的平滑優化改進。 (2)通過對DWA算法中評價函數調整動態加權系數,保證移動機器人在局部路徑規劃中更快避開障礙物并且到達最終目標點。仿真實驗結果表明,減少避障路程和時間,提高避障規劃效率。 (3)Dijkstra算法和DWA算法的融合保證在全局規劃路徑中尋找最優局部路徑,實驗數據表明,移動機器人能夠快速進行路徑規劃,具有實時避障的功能。機器人運動軌跡光滑,過程平穩且較少抖動。且移動機器人重復定位精度≤30 mm,滿足實際應用需求。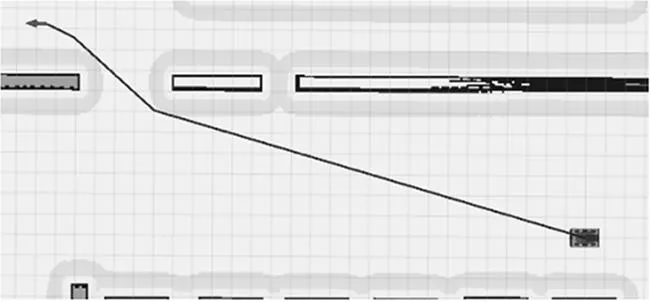
2.4 算法仿真驗證

3 動態窗口法改進及融合仿真
3.1 動態窗口法
3.2 改進DWA算法
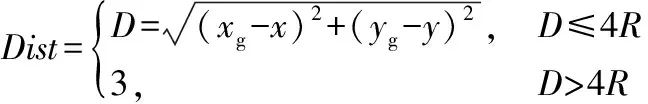

3.3 融合優化算法
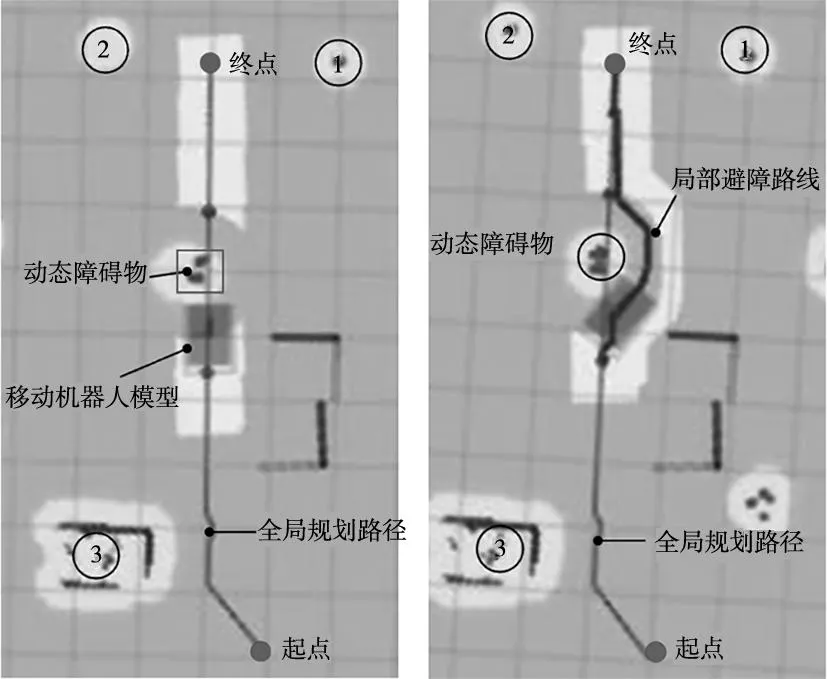
4 樣機實驗及數據分析


5 結論

