大單元背景下的跨學科融合教學的探究

譚新艷

[摘 要] 新課標要求教師豐富教學方式，“探索大單元教學，積極開展跨學科的主題式學習和項目式學習等綜合性教學活動”.“勾股定理”一課，將數學與歷史學科整合，培養學生多學科綜合分析和解決問題的能力.

[關鍵詞]大單元教學；跨學科；勾股定理

基金項目：2022年東莞市年度規劃課題“大單元背景下的初中數學與歷史跨學科教學的實踐研究”（2022GH629）.

新時代召喚新教育，新教育需要新教學.大單元教學是課程的需要，依據《系統論》的基本原理，整體優于部分，整體決定部分，整體大于部分之和，我們需要促進系統內的各構成要素的協同與整合.大單元教學能避免“只見樹木、不見森林”的零散，長期如此學生就能見到一片綠洲.

《義務教育數學課程標準（2022年版）》明確指出：學生通過數學課程的學習，適應現代生活，掌握進一步學習的必備基礎知識、基本技能、基本思想和基本活動經驗.如何達到上述目標？筆者做出如下解釋：將數學學習與生活結合，借鑒歷史經驗完善自己的學習體系.

我們常說，數學來源于生活，生活即數學；我們又說，今天發生的事情將成為歷史，生活即歷史，那么將歷史搬進數學教育是多么的合適.我們可以在數學教學過程中重演歷史，站在巨人的肩上，借鑒別人的經驗完善自己.課堂中教師帶領學生科學地探索歷史，引導學生主動體驗、建構，積累數學基本活動經驗，為長遠學習打下基礎.

跨學科融合教學的實踐

現結合“勾股定理（第1課時）”新授課教學，闡釋如何進行跨學科融合教學，增強學生發現問題、提出問題的意識，提升學生分析問題、解決問題的能力.

1.內容分析

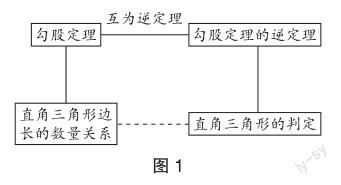
人教版教材八年級下冊第十七章“勾股定理（第1課時）”是章起始課，具有統領全章的作用，思想深刻，育人價值高[1].其教材結構如圖1.

本校學生在七年級上學期的數學寒假作業中，有一項任務是讀一本好書——《奇妙的數學史》，并寫一篇500字以上的讀后感.從批閱讀后感中筆者發現，一位學生對勾股定理印象比較深刻，他借此機會細細揣摩，深入探索了勾股定理這一知識點，并在讀后感中寫道：“我們每個人都是數學家，因為我們發現問題，并努力嘗試解決問題.哪怕這個問題已經被人解答了，但沒關系，因為我挑戰了自己，經歷了由未知到已知的過程，你應該為自己驕傲.”的確如此，對于本課時的教學，我們將采取大單元教學視野下數學融合歷史跨學科教學，激發學生自主學習的欲望.

2.教學目標

（1）了解勾股定理的歷史背景，掌握勾股定理；體會趙爽發現勾股定理的過程.

（2）能通過割補法構造圖形證明勾股定理.

（3）經歷“發現—探索—猜想—驗證”等學習活動，發展學生的幾何直觀、邏輯推理等核心素養，讓學生感受從特殊到一般、數形結合、轉化與化歸等思想方法.

3.教學重點、難點

重點：探索并證明勾股定理.

難點：感悟從特殊到一般、數形結合、轉化與化歸等思想，培養幾何直觀、邏輯推理等核心素養.

4.教學過程

（1）課前小測，喚醒數學思維

填空：

①在△ABC中，∠B=20°，∠C=70°，則∠A= ，△ABC是 三角形.

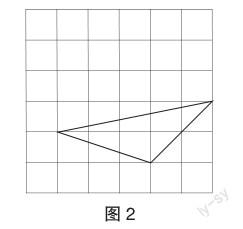
②如圖2，每個小方格正方形的邊長為1個單位，則格點三角形的面積是 .

【教學分析】 課前小測的設計意圖是喚醒本節課相關聯的知識，利用已有的知識解決未知的問題，發展學生的知識遷移能力.學生在學習勾股定理前，已經通過測量、拼圖、折紙等活動，證明了三角形內角和定理，學習了直角三角形兩銳角互余的性質，學生樹立的推理意識以及活動中積累的經驗，都為本節課探究和證明勾股定理奠定了基礎.第②小題通過“割補法”求格點三角形的面積，發展學生的類比思想，因為本節課在探究勾股定理時，需要求格點四邊形的面積.

（2）劇本引入，培養數學興趣

旁白：相傳2500多年前，古希臘著名的哲學家、數學家、天文學家畢達哥拉斯有一次在朋友家做客時，發現朋友家用磚鋪成的地面圖案（如圖3）特別有趣，陷入沉思……

穿著奇特的服裝，掛上絡腮胡子，扮演畢達哥拉斯的學生一出場，立刻引得全班同學哈哈大笑.“畢達哥拉斯”盯著地板，左看看右看看，興奮地自言自語道：“好奇妙，這圖案中竟含有這樣特殊的數量關系，太神奇了！”

【教學分析】 畢達哥拉斯激發了學生的好奇心，學生迫不及待想知道畢達哥拉斯發現了什么.學生帶著好奇心，走進歷史長河，走進畢達哥拉斯的世界，歷經知識的演變.

（3）任務驅動，積累活動經驗

教師設計富有挑戰性的學習任務，教學時給學生發放一頁講義，講義上有四幅7×7的格點圖（如圖4），提出了三個任務：①利用下列網格，畫出幾個格點正方形；②關于畫出的正方形，你發現了什么？③結合圖形說說你是如何求這些正方形的面積的.