帶人字槽和軸向微通槽的動靜壓氣體軸承靜態(tài)特性
李樹森,馬添瀟,穆巖璞
(東北林業(yè)大學(xué)機電工程學(xué)院,黑龍江哈爾濱 150040)
超精軸承作為影響超精密加工的核心因素,對提升制造業(yè)水平具有舉足輕重的作用[1]。在各種超精軸承中,動靜壓氣體軸承相比靜壓氣體軸承和動壓氣體軸承有著承載特性好和穩(wěn)定性較優(yōu)等優(yōu)點,為此學(xué)者們對其進行了深入研究。李樹森等[2]以人字槽小孔節(jié)流動靜壓氣體軸承為研究對象,對氣體軸承的氣膜流場特性和承載特性進行了分析。王欣崎等[3]以螺旋槽小孔節(jié)流動靜壓氣體軸承為研究對象,研究槽深、槽寬等參數(shù)對靜態(tài)特性的影響。于賀春等[4]分析了人字槽狹縫節(jié)流動靜壓混合氣體軸承,并通過仿真優(yōu)化了該軸承設(shè)計參數(shù)。李樹森等[5]以小孔節(jié)流深淺腔動靜壓氣體軸承為研究對象,采用Fluent軟件對軸承的承載特性進行分析。賈晨輝等[6]以球面螺旋槽動靜壓氣體軸承為研究對象,研究了瞬態(tài)剛度和阻尼的震動特征。王廣洲等[7]以人字槽狹縫節(jié)流氣體軸承為研究對象,對其靜態(tài)特性進行了研究。汲騰龍等[8]以狹縫節(jié)流動靜壓氣體徑向滑動軸承為對象,對其承載能力和穩(wěn)定性進行了研究。
為了改進現(xiàn)有氣體軸承剛度和承載能力不足的缺點,本文作者設(shè)計了一種新型帶人字槽和軸向微通槽的動靜壓氣體軸承,利用Fluent分析氣體軸承的承載特性,研究軸向微通槽深度、偏心率、氣膜厚度、供氣壓力對氣體軸承承載能力和剛度的影響規(guī)律。
1 帶人字槽和軸向微通槽動靜壓氣體軸承的設(shè)計
動靜壓氣體軸承的工作原理是動壓氣體軸承和靜壓氣體軸承工作原理的混合疊加,使軸承在啟停階段因氣體潤滑產(chǎn)生靜壓承載,在主軸高速旋轉(zhuǎn)時因氣體的動壓效應(yīng)產(chǎn)生動壓承載,進一步提升整個軸承的承載能力[9]。
為進一步提升氣體軸承剛度和承載能力,設(shè)計了帶人字槽和軸向微通槽的動靜壓氣體軸承的結(jié)構(gòu),如圖1所示。人字槽可以使動靜壓氣體軸承產(chǎn)生動壓效應(yīng)以提升承載能力,軸向微通槽可以使壓力均化,避免由小孔節(jié)流產(chǎn)生氣錘自激的振動現(xiàn)象。

圖1 帶人字槽和軸向微通槽動靜壓氣體軸承結(jié)構(gòu)示意
設(shè)計的軸承上具有小孔節(jié)流器,并在小孔節(jié)流器之間開設(shè)軸向微通槽。主軸上開設(shè)雙排人字槽,每排10個。同時主軸上開設(shè)雙排供氣孔,每排8個。軸向微通槽沿軸承內(nèi)側(cè)圓周方向均勻開設(shè),共開設(shè)有8個,用以連接同一軸線上不同的兩排小孔節(jié)流器出氣口。
圖1中,D1為軸承外徑,D2為軸承內(nèi)徑,L為軸承長度,d為主軸直徑,h為氣膜厚度,β為人字槽槽角,ds為節(jié)流孔直徑,h0為軸向微通槽深度,b0為軸向微通槽寬度,l1為孔邊距,l2為孔距,hg為人字槽深度,bg為人字槽槽寬,br為人字槽槽臺寬。初步確定主軸和軸承的結(jié)構(gòu)參數(shù)和工作參數(shù)如表1所示。
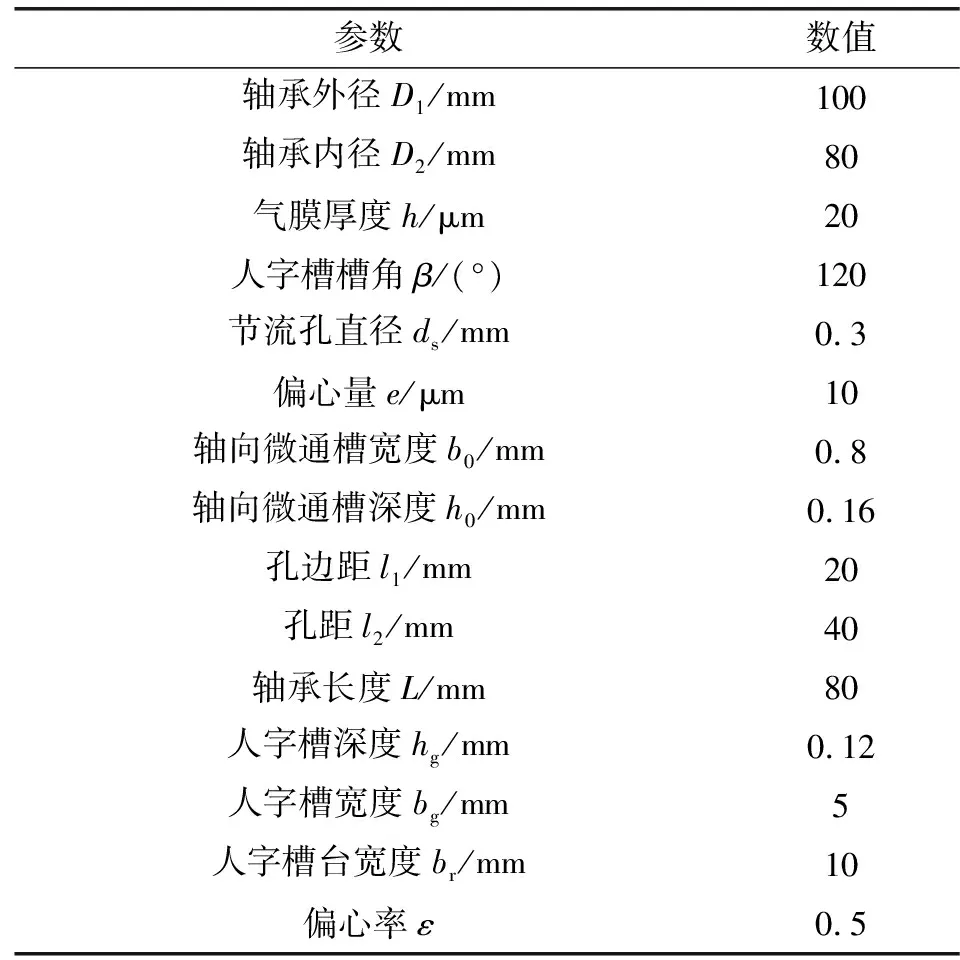
表1 軸承的結(jié)構(gòu)參數(shù)和工作參數(shù)
2 靜態(tài)特性理論分析及仿真模型建立
2.1 帶人字槽和軸向微通槽動靜壓氣體軸承靜態(tài)特性分析
利用有限元分析法求解雷諾方程,對帶人字槽軸向微通槽的動靜壓氣體軸承進行靜態(tài)特性分析。
假設(shè)氣體為理想氣體,黏性系數(shù)為常數(shù),氣體流動為等溫過程,考慮氣體的可壓縮性,氣體在氣膜間隙中不存在相對滑動。基于上述假設(shè)推導(dǎo)的雷諾方程如式(1)[10-13]所示。
(1)
式中:p為壓力函數(shù);ρ為流體密度;μ為氣體動力黏度;vx、vz為氣流速度分量。
引入量綱一化參數(shù),取p0、hm、L為參考量,可得量綱一化雷諾方程如式(2)所示。
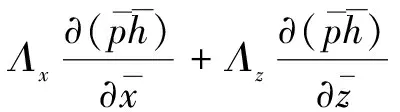
(2)
將狄利克雷函數(shù)δi引入,得到簡化后的雷諾方程式(3)。
(3)
動靜壓氣體軸承的承載力為氣體軸承在靜壓階段的承載力和氣體軸承在外部氣源停止供氣后軸承高速穩(wěn)定工作時的承載力相互耦合所得出,只需分別求出氣體軸承在靜壓和動壓工作狀態(tài)下的承載力,就可求得動靜壓氣體軸承的承載力,如式(4)所示。
W=Ws+Wd
(4)
計算靜壓階段的承載力時,利用有限元分析的方法將氣膜分割成n個單元體,并分別求解每個單元體的承載力Wλ,然后對所有單元體的承載力耦合從而求得軸承在靜壓階段的總承載力Ws,如式(5)所示。
(5)
人字槽動靜壓氣體軸承在動壓階段的承載力Wd按文獻[14]中公式,如式(6)所示。
(6)
動靜壓氣體軸承的剛度K可由承載能力的變化量和氣膜厚度變化量得出,如式(7)所示。
(7)
2.2 建立仿真模型
利用Gambit軟件對軸承的氣膜模型進行網(wǎng)格劃分。四面體網(wǎng)格在自動化、效率、可靠性以及幾何通用性上要強于六面體網(wǎng)格,利用2階的四面體進行網(wǎng)格劃分可保證有限元分析的整體精度。由于氣體軸承在空間3個方向的尺寸大小相差較大,氣膜厚度一般在幾十微米范圍內(nèi),在網(wǎng)格生成時為了減小網(wǎng)格負(fù)體積出現(xiàn)的概率,文中使用了分塊結(jié)構(gòu)化網(wǎng)格的劃分方法,劃分結(jié)果如圖2(a)所示。網(wǎng)格無關(guān)性驗證如圖2(b)所示。可見,當(dāng)節(jié)點數(shù)達到50萬后,計算的承載力不再變化,為了提高數(shù)值計算精度和控制計算時間,下文采用節(jié)點數(shù)50萬進行計算。
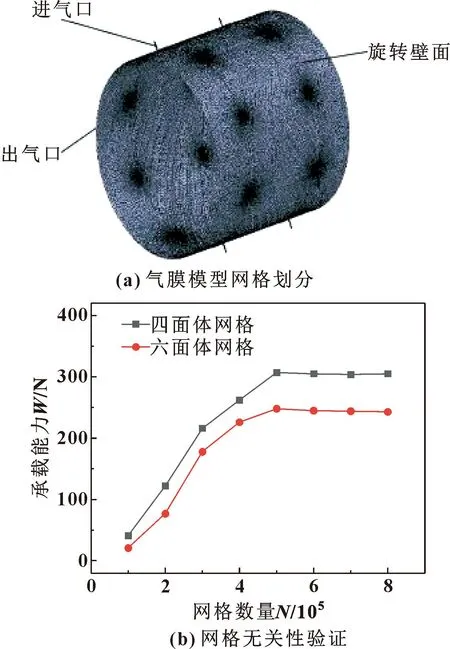
圖2 氣膜模型網(wǎng)格劃分及網(wǎng)格無關(guān)性驗證
2.3 假設(shè)條件及邊界條件的設(shè)定
假設(shè)條件設(shè)定:(1)在理論建模時,忽略潤滑氣體的慣性力和體積力對氣膜的影響;(2)將潤滑氣體視為不可壓縮氣體,在潤滑過程中氣體連續(xù)、定常且整個潤滑過程與外部無熱能交換,為絕熱過程;(3)將潤滑氣體視為牛頓流體;(4)假設(shè)潤滑氣體在流動時為層流狀態(tài)。
模型采用壓力進出口邊界和壁面邊界,16個進氣口設(shè)置壓力為ps=0.4 MPa,出口邊界壓力設(shè)為pa=0.102 MPa;主軸轉(zhuǎn)速n=1×104r/min;偏心率設(shè)置為0.5;壁面為移動邊界,方向設(shè)置為旋轉(zhuǎn);流體介質(zhì)為理想氣體并為常溫流動,湍流模型采用k-εSST模型[15],并且開啟曲率矯正從而保證邊界層的梯度精度。
3 仿真結(jié)果與分析
3.1 供氣壓力對靜態(tài)特性的影響
固定其他參數(shù),分別選取供氣壓力為0.4、0.5、0.6、0.7、0.8 MPa,分析偏心率的變化對軸承剛度及承載能力的影響規(guī)律,結(jié)果如圖3所示。

圖3 不同供氣壓力下軸承剛度和承載力隨偏心率的變化
由圖3可知,在偏心率固定不變的情況下動靜壓氣體軸承的剛度和承載能力隨供氣壓力增大而增大,這主要是因為供氣壓力增大引起氣膜壓力增大;在相同供氣壓力下,隨著偏心率增大,軸承的剛度不斷減小,在偏心率從0.1到0.4增大時,軸承剛度減小的速度較為緩慢,在偏心率從0.4到0.8增大時,軸承剛度減小的速度不斷增加;在相同供氣壓力下,隨著偏心率的增大,動靜壓氣體軸承的承載能力不斷增大,偏心率從0.1到0.6增大時,軸承的承載能力增大速度較快,偏心率從0.6到0.8增大時,軸承的承載能力增大緩慢。由上述結(jié)果可知,當(dāng)動靜壓氣體軸承的偏心率過大時無法保證氣體軸承的剛度要求,偏心率過小則無法保證承載能力的要求,設(shè)計氣體軸承時應(yīng)選擇合適的偏心率,以同時滿足軸承的承載能力和剛度的要求。
3.2 不同參數(shù)下人字槽對靜態(tài)特性的影響
固定其他參數(shù),在不同轉(zhuǎn)速、偏心率、供氣壓力和氣膜厚度下對比研究了有、無人字槽時氣體軸承的剛度和承載能力變化規(guī)律,結(jié)果如圖4—7所示。
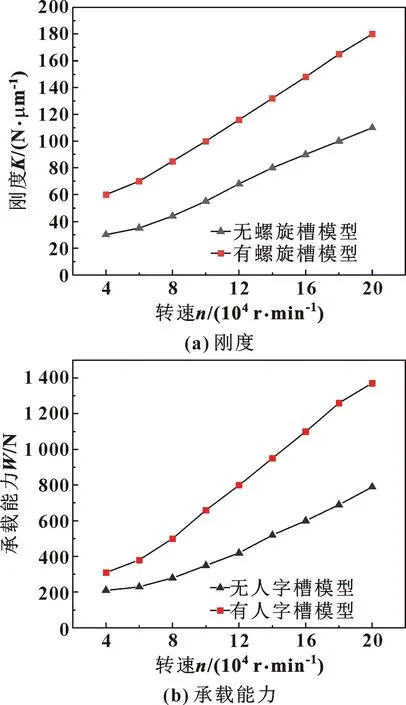
圖4 有、無人字槽氣體軸承的剛度和承載能力隨主軸轉(zhuǎn)速的變化
由圖4可以看出,在同一主軸轉(zhuǎn)速條件下,相較不帶人字槽的氣體軸承,帶人字槽的氣體軸承的承載能力和剛度都顯著提高,且隨著主軸轉(zhuǎn)速不斷提升,二者的差距不斷增大,這主要是因為隨著轉(zhuǎn)速提升人字槽產(chǎn)生的動壓效應(yīng)不斷增強。由圖5—7可知,帶人字槽的氣體軸承承載能力和剛度均高于不帶人字槽的氣體軸承,這主要是因為在主軸高速轉(zhuǎn)動時,人字槽可以產(chǎn)生壓力升,從而增大動靜壓氣體軸承的剛度和承載能力。
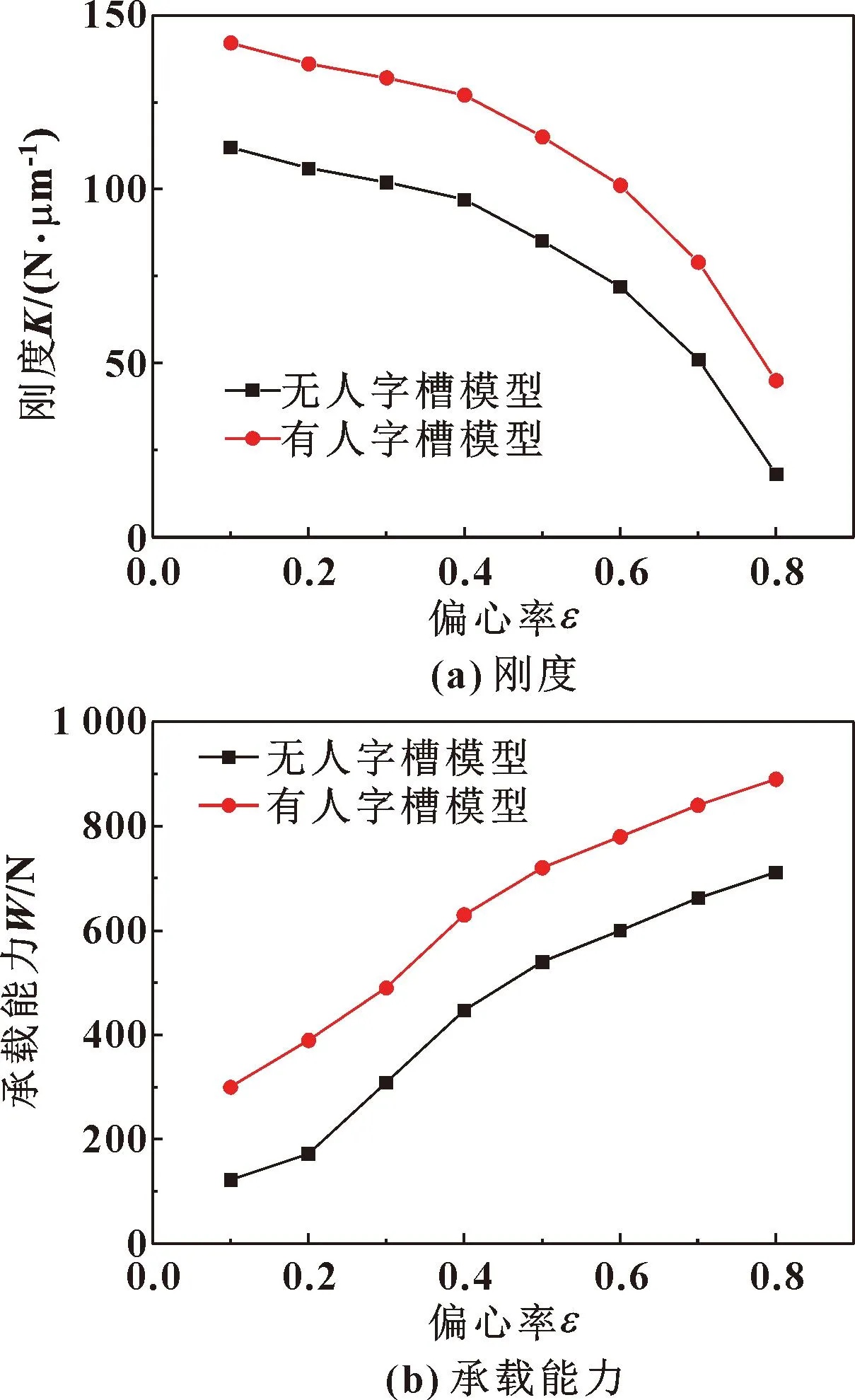
圖5 有、無人字槽時氣體軸承的剛度和承載能力隨偏心率的變化

圖6 有、無人字槽時氣體軸承的剛度和承載能力隨供氣能力的變化

圖7 有、無人字槽時氣體軸承的剛度和承載能力隨氣膜厚度的變化
3.3 軸向微通槽深度對靜態(tài)特性的影響
由以往的研究可知,帶軸向微通槽的動靜壓氣體軸承在氣膜厚度為15~25 μm的情況下具有較高的承載力和剛度[16],故選取氣膜厚度分別為15、20、25 μm,固定其他參數(shù),研究軸向微通槽深度對軸承的剛度及承載能力的影響規(guī)律,如圖8所示。
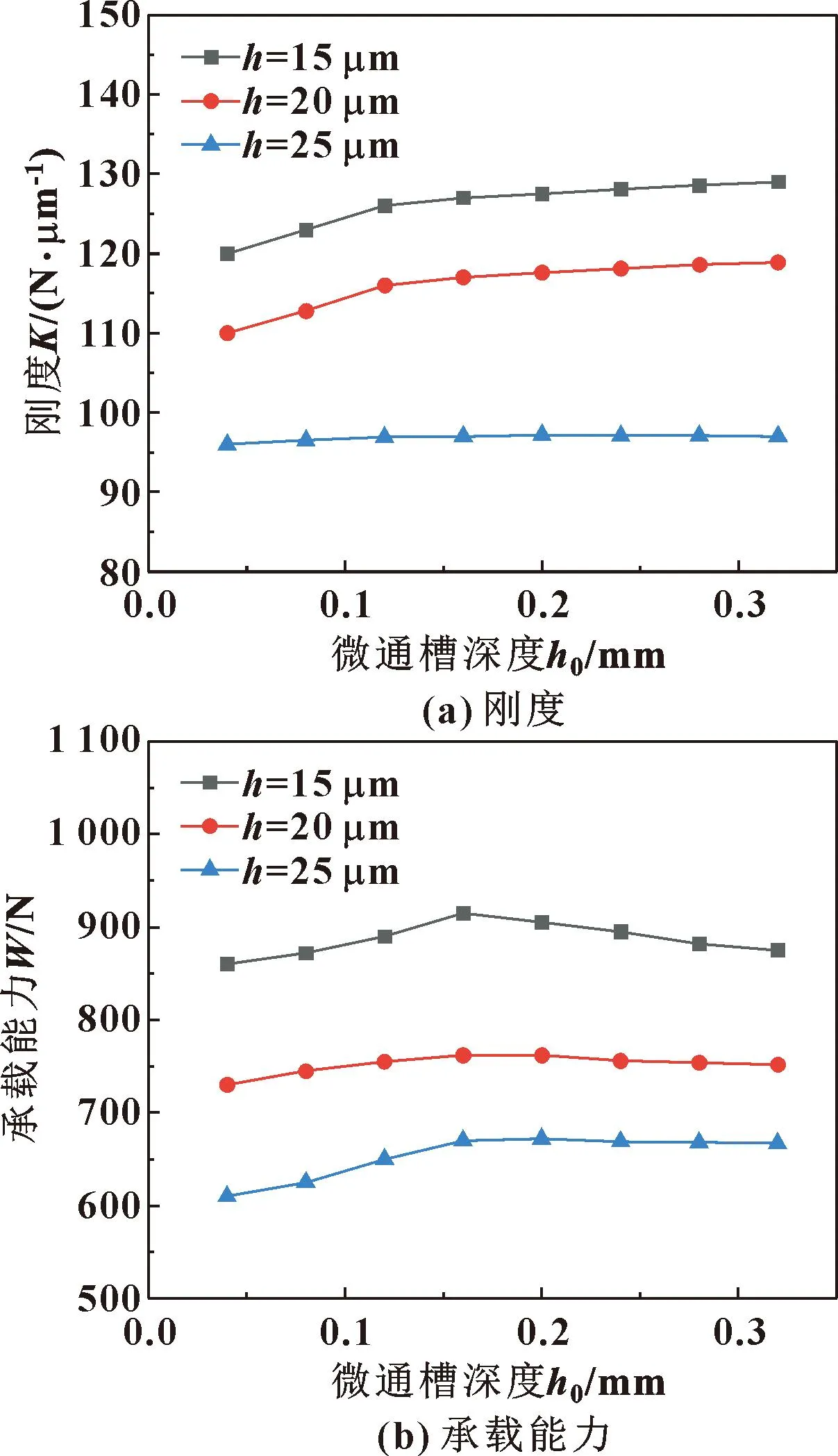
圖8 不同氣膜厚度下承載力和剛度隨微通槽深度的變化
由圖8可以看出,在同一微通槽深度下,軸承剛度和承載能力隨著氣膜厚度增大而減小;軸承剛度隨著微通槽深度不斷增大而增大,但在微通槽深度達到0.2 mm以后軸承的剛度提升變得十分不明顯;軸承承載能力隨著微通槽深度增大先增大,但當(dāng)微通槽深度達到0.2 mm以后軸承的承載能力出現(xiàn)下降的趨勢。上述結(jié)果表明,當(dāng)氣膜厚度為15、20、25 μm時,選用微通槽深度為0.16~0.2 mm的軸向微通槽,氣體軸承的靜態(tài)特性最佳。
3.4 仿真方法可靠性驗證
利用MatLab軟件對式(1)進行理論求解,得到帶人字槽和軸向微通槽的動靜壓氣體軸承在偏心率為0.5時軸承承載能力隨轉(zhuǎn)速的變化曲線,如圖9所示。可見,理論計算結(jié)果與文中仿真結(jié)果基本一致,從而驗證仿真方法的可靠性。理論曲線與仿真曲線有細(xì)小偏差主要是由于四面體網(wǎng)格精度有限,造成仿真結(jié)果與理論值有一定差異。

圖9 理論求解與仿真分析結(jié)果對比
4 結(jié)論
對設(shè)計的帶人字槽和軸向微通槽的動靜壓氣體軸承靜態(tài)特性進行仿真分析,研究不同結(jié)構(gòu)參數(shù)和工作參數(shù)對軸承靜態(tài)特性的影響規(guī)律,結(jié)論如下:
(1)偏心率保持不變的情況下,隨著供氣壓力的升高,氣體軸承的承載能力和剛度同時增大;隨著偏心率增大,軸承剛度減小,承載能力增大。
(2)開設(shè)人字槽可以產(chǎn)生動壓效應(yīng)提升軸承的承載能力,主軸轉(zhuǎn)速提高可以使動壓效應(yīng)增強從而改善氣體軸承的承載能力和剛度。
(3)增大微通槽深度對提升氣體軸承的剛度和承載能力有一定幫助,但當(dāng)微通槽深度過大時,軸承承載能力會減小。

