基于單電極激勵模式的顱腦電阻抗圖像重建方法研究

王萌 鄭碩 施艷艷 廖娟娟

摘 要：作為一種新興的可視化技術(shù)，電阻抗層析成像（EIT）能夠根據(jù)人體組織病理變化對其電導(dǎo)率分布進(jìn)行圖像重建，為疾病檢測提供了一種選擇.在基于EIT的腦部疾病檢測中，為了改善被測區(qū)域的靈敏度分布并解決電阻抗成像中典型的不適定問題，在單電極激勵數(shù)據(jù)采集模式下，提出了k階有限差分L₁正則化目標(biāo)函數(shù)，并采用增廣拉格朗日和交替方向算法對目標(biāo)函數(shù)進(jìn)行求解，實(shí)現(xiàn)電導(dǎo)率分布的重構(gòu).研究了單電極激勵模式下，外接電阻對敏感場的影響；針對腦出血和腦缺血兩種病情，對比了Landweber方法、Newton-Raphson方法、Tikhonov方法、廣義總變分方法（TGV）和本文方法的圖像重建性能.結(jié)果表明，在腦出血和腦缺血的圖像重建中，采用單電極激勵模式的ALAD-LR方法可有效提高圖像重建質(zhì)量，并具有較強(qiáng)的魯棒性.

關(guān)鍵詞：電阻抗成像；圖像重建；單電極激勵；正則化方法

中圖分類號：TH772文獻(xiàn)標(biāo)志碼：A文章編號：1000-2367（2024）02-0089-07

腦出血、腦缺血是常見的腦部疾病，其致殘和死亡風(fēng)險高.及時、準(zhǔn)確地檢測腦出血和腦缺血是保證腦疾病康復(fù)的關(guān)鍵.目前，計算機(jī)斷層掃描（computed tomography，CT）和磁共振成像（magnetic resonance imaging，MRI）技術(shù)是常用的診斷手段.然而，CT具有放射性，不便于攜帶，MRI檢測價格昂貴，檢測結(jié)果需要較長時間等待，不能連續(xù)監(jiān)測.電阻抗層析成像（electrical impedance tomography，EIT）作為一種新興的可視化技術(shù)，與傳統(tǒng)技術(shù)相比具有安全、快速、便攜、無創(chuàng)、連續(xù)監(jiān)測和成本低廉等優(yōu)點(diǎn)^［1-2］.EIT技術(shù)可以直觀地顯示被檢測物體內(nèi)部的電導(dǎo)率分布，實(shí)現(xiàn)電導(dǎo)率分布的可視化，在生物醫(yī)學(xué)^［3］和工業(yè)檢測^［4］中具有廣闊的應(yīng)用前景.

EIT圖像重建的數(shù)學(xué)本質(zhì)為非線性病態(tài)逆問題的求解^［5］.然而，由于測量數(shù)據(jù)有限，EIT重建圖像的空間分辨率通常較低.為了解決這一問題，國內(nèi)外學(xué)者提出了多種圖像重建方法，如：正則化方法^［6］、貝葉斯方法^［7］、深度學(xué)習(xí)方法^［8］等.其中，正則化方法通過在目標(biāo)函數(shù)中加入懲罰項來約束解，可實(shí)現(xiàn)病態(tài)問題的穩(wěn)定求解，在EIT中應(yīng)用最為廣泛^［9］.LEE等^［10］在正則化過程中引入雅可比矩陣，采用基于運(yùn)動偽影抑制濾波器的新型保真嵌入正則化方法，能夠在有噪聲的情況下穩(wěn)定地重構(gòu)高保真圖像.為了避免合理數(shù)據(jù)丟失，F(xiàn)AN等^［11］提出了一種基于L_1/2正則化的改進(jìn)算法，將L_1/2范數(shù)作為懲罰項的形式，利用8個鄰域的梯度特征來檢索可能被過濾掉的合理數(shù)據(jù).為了解決Tikhonov方法使重建圖像邊緣過度光滑的問題，SONG等^［12］提出了一種將Tikhonov正則化方法與TV正則化方法相結(jié)合的混合正則化方法，該方法將電導(dǎo)率梯度函數(shù)作為自適應(yīng)加權(quán)參數(shù)，自動控制TV懲罰項與Tikhonov正則化懲罰項之間的加權(quán)，進(jìn)而提高成像質(zhì)量.上述圖像重建方法雖然一定程度上提高了成像質(zhì)量，但仍存在背景偽影較多、目標(biāo)物的位置和形狀不準(zhǔn)確等問題.

針對現(xiàn)有圖像重建方法的不足，本文在單電極激勵模式下提出了一種k階有限差分L₁正則化目標(biāo)函數(shù)，并采用增廣拉格朗日和交替方向算法對目標(biāo)函數(shù)進(jìn)行求解，即一種基于增廣拉格朗日和交替方向算法的L₁正則化（augmented lagrangian and alternating direction L₁regularization，ALAD-LR）圖像重構(gòu)方法.該方法引入k階有限差分L₁范數(shù)作為懲罰項，以充分利用k階有限差分的弱導(dǎo)數(shù)特性，并在目標(biāo)函數(shù)等價變換中引入了松弛變量Q，該變量可將不可微‖G^kg‖的項轉(zhuǎn)換出可微的G^kg項，有利于求解變量g的最優(yōu)值.研究了腦出血和腦缺血病情下的圖像重建性能，并與Tikhonov、廣義總變分（total generalized variation，TGV）正則化方法以及Landweber、Newton-Raphson等非正則化方法的圖像重建性能進(jìn)行對比.結(jié)果表明，在腦出血和腦缺血的圖像重建中，k階有限差分的弱導(dǎo)數(shù)特性以及松弛變量Q的引入使本文方法表現(xiàn)出較好的重建效果和較強(qiáng)的魯棒性.

1 單電極激勵模式基本原理

與相鄰、相對激勵模式相比，單電極激勵模式的電極接觸阻抗相對較小，獨(dú)立測量數(shù)據(jù)多，且每個電極都有電流流過，可獲得較為均勻的敏感場分布.此外，單電極激勵模式輸出電阻引入大量的接地點(diǎn)，所以對外界的抵抗性較好，并且通過改變外界電阻可以改變整個敏感場的特性.因此，本文采用電流激勵、電流測量的單電極激勵檢測模式.

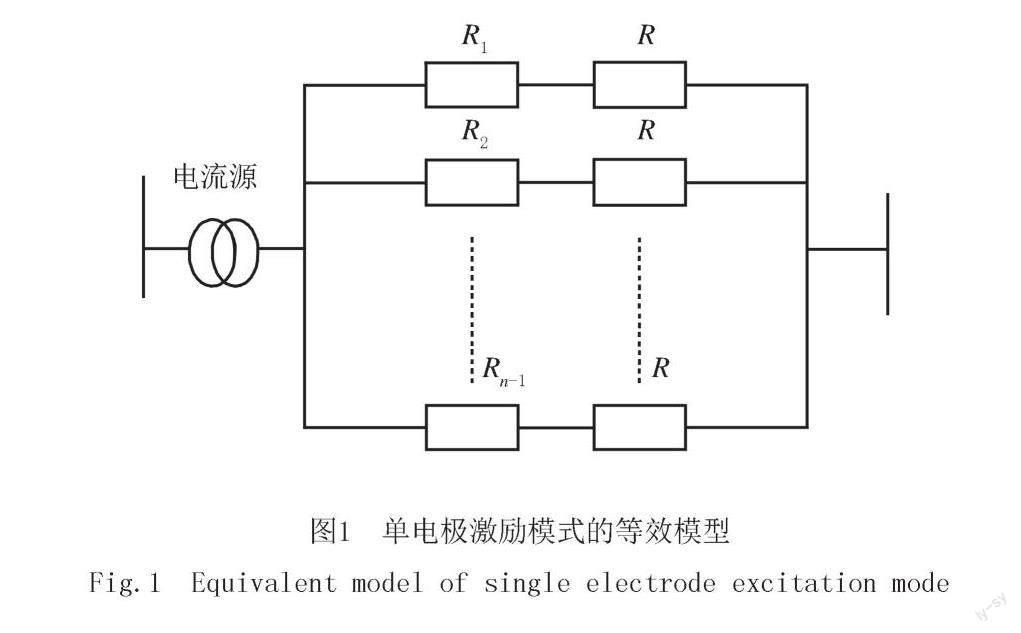
根據(jù)單電極激勵模式的電路結(jié)構(gòu)特點(diǎn)，其等效模型可由電路并聯(lián)形式表示：在n電極EIT系統(tǒng)中，1個電極作為激勵電流輸入端，其余n-1個電極作為電流輸出端，可得到n-1個激勵檢測支路，其等同于n-1個并聯(lián)電路的各個支路.如圖1所示，每一對激勵電極、檢測電極之間的電阻與外接電阻形成一個支路，每個支路電壓相等.其中，R₁，R₂，…，R_n-1是激勵電極與檢測電極之間的電阻，R是外接電阻.通過測量外接電阻端電壓，可計算出流過每個電極的電流，進(jìn)而獲得測量數(shù)據(jù).

本文選用16電極模型，如圖2所示，向任意一個電極輸入激勵電流，并測量其余15個電極的外接電阻端電壓，經(jīng)過計算可得到15個電流值.以此類推，循環(huán)激勵16個電極可得到16組數(shù)據(jù)，每組數(shù)據(jù)包含15個測量值，共獲得240個測量數(shù)據(jù).

2 基于增廣拉格朗日和交替方向算法的L₁正則化方法

為了解決現(xiàn)有方法重建圖像中背景偽影多、目標(biāo)物位置和形狀不準(zhǔn)確的問題.本文在EIT逆問題求解中提出了一種k階有限差分L₁正則化目標(biāo)函數(shù)，并采用增廣拉格朗日和交替方向算法對目標(biāo)函數(shù)進(jìn)行求解，用于重構(gòu)電阻抗成像中的電導(dǎo)率分布.所提出的目標(biāo)函數(shù)

3 結(jié)果及數(shù)據(jù)分析

現(xiàn)有單電極激勵模式研究主要針對工業(yè)多相流電阻層析成像領(lǐng)域.與多相流電阻層析成像不同，在顱腦電阻抗層析成像中由于顱骨電導(dǎo)率較低以及電極和被測對象（腦組織）不能直接接觸.因此，單電極激勵模式在顱腦電阻抗成像的應(yīng)用效果還需要進(jìn)一步分析.圖3給出了單電極、相鄰、相對3種激勵模式的靈敏度分布.由圖3可以看出，單電極激勵模式和相對激勵模式的靈敏度分布相近均明顯優(yōu)于相鄰激勵模式.此外，相鄰激勵、相對激勵以及單電極激勵可以獲得的測量數(shù)據(jù)分別為208、192和240個.因此，在相同靈敏度分布條件下，單電極激勵模式可以獲得更多的測量數(shù)據(jù)，對逆問題求解更有優(yōu)勢.另外，單電極激勵模式在系統(tǒng)設(shè)計上引入了外接電阻，調(diào)節(jié)外接電阻的大小將對靈敏場的性能產(chǎn)生影響.圖4為外接電阻分別為10、20、30 Ω時的靈敏度分布情況.由圖4可以看出，外接電阻越大靈敏度分布越均勻，但外接電阻過大會阻礙激勵電流到達(dá)測量區(qū)域中心位置，導(dǎo)致測量精度降低.因此，綜合考慮靈敏度分布均勻性和測量精度，本文采用20 Ω的外接電阻.

3.1 無噪條件下腦出血/腦缺血圖像重建

在EIT的研究中，為了便于分析，通常將顱腦模型簡化為由頭皮、顱骨、腦組織組成的三層圓形模型，其中頭皮電導(dǎo)率為0.44 S/m，顱骨電導(dǎo)率為0.012 6 S/m，腦組織電導(dǎo)率為0.15 S/m.在腦出血圖像重建中，目標(biāo)物的電導(dǎo)率為0.7 S/m，重建結(jié)果如圖5所示.在腦缺血圖像重建中，目標(biāo)物的電導(dǎo)率為0.05 S/m，重建結(jié)果如圖6所示.需要說明的是，為了清晰表示腦出血或腦缺血的位置，重建圖像第一列為腦出血或腦缺血的示意圖.另外，分別采用Landweber、Newton-Raphson、Tikhonov、TGV方法與本文方法進(jìn)行了成像對比.上述方法所使用的參數(shù)由經(jīng)驗(yàn)法選擇，選擇過程如下：每個參數(shù)設(shè)置在一定范圍內(nèi)，并進(jìn)行循環(huán)計算，直到找到重建質(zhì)量評價指標(biāo)最優(yōu)時對應(yīng)的參數(shù).Landweber、Newton-Raphson方法的電導(dǎo)率初值分別為αA^TB和A^TB，步長分別為0.100和0.009.Tikhonov方法的正則化參數(shù)為0.002.TGV方法正則化參數(shù)為10^-6，電導(dǎo)率初值為0，權(quán)重因子α₁=4，α₀=0.001.本文方法的相關(guān)參數(shù)設(shè)置為：k=0.1，正則化參數(shù)為0.003，電導(dǎo)率初值為A^TB，步長由式（1）計算，懲罰項參數(shù)η和τ均為8，內(nèi)迭代和外迭代次數(shù)分別設(shè)定為9和10.上述迭代方法的終止條件為：達(dá)到設(shè)定的迭代次數(shù)時算法終止.

由圖5和圖6可以看出，Landweber方法重建的圖像質(zhì)量最差，重建圖像比真實(shí)目標(biāo)物明顯偏大，且不能清晰地分辨出目標(biāo)物的邊界；與Landweber方法相比，Newton-Raphson方法重建的圖像得到了一定改善，但效果亦不理想；Tikhonov正則化方法雖然是直接求解算法，但是有二范數(shù)懲罰項的加入，提高了解的穩(wěn)定性，因此，Tikhonov方法相比Landweber方法更具有優(yōu)勢；然而，采用Tikhonov方法和TGV方法時，目標(biāo)物的大小和形狀仍然沒有得到準(zhǔn)確地重建，圖像包含有明顯偽影；與以上方法相比，本文方法的重建目標(biāo)物大小和形狀更精確、邊界更清晰、背景偽影較少，圖像質(zhì)量得到明顯的改善.

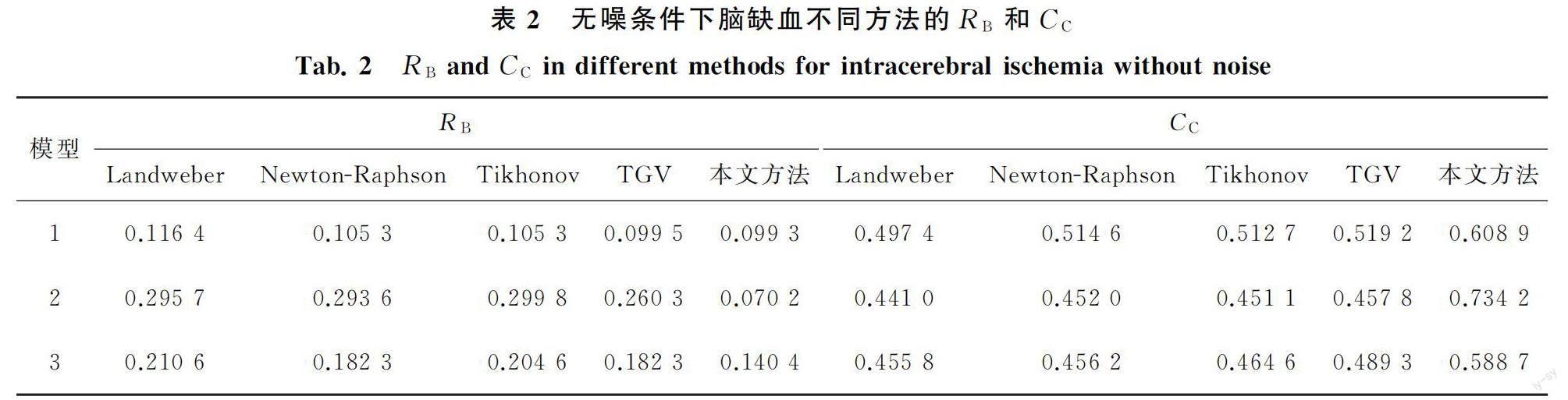
在無噪條件下，腦出血圖像重建時5種方法的R_B和C_C分別如表1所示，腦缺血圖像重建時5種方法的R_B和C_C分別如表2所示.由表1和表2可以看出，本文方法在3種模型條件下的R_B皆是最低的，C_C皆是最高的.因此，本文方法重建的圖像優(yōu)于其他4種方法.

3.2 10%噪聲條件下腦出血/腦缺血圖像重建

在實(shí)際應(yīng)用中，噪聲對圖像重建的影響不可忽略.為了研究本文方法在有噪聲情況下的圖像重建性能，在測量邊界電流時，加入高斯白噪聲，表示為I_noise=I+e，I_noise和I分別表示有噪聲和無噪聲的電流，e表示均值為零、方差為（c·I）²的高斯白噪聲，c為噪聲水平，即噪聲水平為10%時c=10%.為了便于理解，將10%的噪聲轉(zhuǎn)換為信噪比的形式為20 dB.

在噪聲水平為10%條件下5種方法的圖像重建結(jié)果分別如圖7和圖8所示.在噪聲的影響下，5種方法重建的圖像目標(biāo)物比真實(shí)圖像目標(biāo)物大.與Landweber、Newton-Raphson、Tikhonov、TGV方法相比，本文方法對噪聲表現(xiàn)出較強(qiáng)的魯棒性，重建的目標(biāo)物更接近真實(shí)圖像中的目標(biāo)物，且背景中偽影較少.需要說明的是，由于噪聲的影響，5種方法重建圖像中目標(biāo)物發(fā)生形變，但是本文方法仍然表現(xiàn)出較好的性能.

由表3和表4可以看出，本文方法的R_B最小，C_C最高，進(jìn)一步證明了本文方法的魯棒性.

4 結(jié) 論

為了解決現(xiàn)有EIT成像方法重建圖像背景偽影多、目標(biāo)物位置和形狀不準(zhǔn)確的問題，分析比較了單電極模式、相鄰模式、相對模式的靈敏度分布特性，研究了單電極模式外接電阻對靈敏度分布的影響，實(shí)現(xiàn)對被測區(qū)域靈敏度分布的優(yōu)化.進(jìn)一步，提出了單電極激勵模式下k階有限差分L₁正則化目標(biāo)函數(shù)，并采用增廣拉格朗日和交替方向算法對目標(biāo)函數(shù)進(jìn)行求解.在無噪聲和有噪聲條件下，研究比較了Landweber方法、Newton-Raphson方法、Tikhonov方法、TGV方法和本文方法對腦出血和腦缺血兩種病情的圖像重建性能，并通過模糊半徑（R_B）和相關(guān)系數(shù)（C_C）指標(biāo)對成像質(zhì)量進(jìn)行定量評價.結(jié)果表明，本文方法可明顯改善圖像重建質(zhì)量，并表現(xiàn)出較強(qiáng)的魯棒性.

參 考 文 獻(xiàn)

［1］BAI X，SUN J T，BAI X，et al.A modified noise model of electrical impedance tomography system by considering colored noises［J］.IEEE Transactions on Instrumentation and Measurement，2022，71：1001910.

［2］劉學(xué)超，張濤，章偉睿，等.腦脊液變化對腦出血電阻抗成像表征的影響研究［J］.中國醫(yī)學(xué)裝備，2022，19（1）：26-30.

LIU X C，ZHANG T，ZHANG W R，et al.A study on the influence of the CSF changes on EIT representation of cerebral hemorrhage［J］.China Medical Equipment，2022，19（1）：26-30.

［3］KIRCHER M，ELKE G，STENDER B，et al.Regional lung perfusion analysis in experimental ARDS by electrical impedance and computed tomography［J］.IEEE Transactions on Medical Imaging，2021，40（1）：251-261.

［4］LI K，WANG Q，WANG M.Three-dimensional visualisation of gas-water two-phase flow based on bubble mapping method and size projection algorithm［J］.Flow Measurement and Instrumentation，2019，69：101590.

［5］閆孝姮，呂秋皓，林曉雪，等.基于Tikhonov和TV混合正則化的接地網(wǎng)電阻抗成像算法研究［J］.儀器儀表學(xué)報，2021，42（11）：160-171.

YAN X H，LYU Q H，LIN X X，et al.Research on grounding grid electrical impedance tomography algorithm based on Tikhonov and TV hybrid regularization［J］.Chinese Journal of Scientific Instrument，2021，42（11）：160-171.

［6］SHI Y Y，KONG X L，WANG M，et al.A non-convex L₁-norm penalty-based total generalized variation model for reconstruction of conductivity distribution［J］.IEEE Sensors Journal，2020，20（14）：8137-8146.

［7］MA G，CHEN H F，WANG P，et al.Multi-frame constrained block sparse Bayesian learning for flexible tactile sensing using electrical impedance tomography［J］.IEEE Transactions on Computational Imaging，2022，8：438-448.

［8］FAN Y W，YING L X.Solving electrical impedance tomography with deep learning［J］.Journal of Computational Physics，2020，404：109119.

［9］SHI Y Y，ZHANG X，RAO Z G，et al.Reduction of staircase effect with total generalized variation regularization for electrical impedance tomography［J］.IEEE Sensors Journal，2019，19（21）：9850-9858.

［10］LEE K，WOO E J，SEO J K.A fidelity-embedded regularization method for robust electrical impedance tomography［J］.IEEE Transactions on Medical Imaging，2018，37（9）：1970-1977.

［11］FAN W R，WANG C.A modified L_1/2regularization algorithm for electrical impedance tomography［J］.Measurement Science and Technology，2020，31（1）：015011.

［12］SONG X Z，XU Y B，DONG F.A hybrid regularization method combining Tikhonov with total variation for electrical resistance tomography［J］.Flow Measurement and Instrumentation，2015，46：268-275.

［13］JAVAHERIAN A，MOVAFEGHI A，F(xiàn)AGHIHI R，et al.An exhaustive criterion for estimating quality of images in electrical impedance tomography with application to clinical imaging［J］.Journal of Visual Communication and Image Representation，2013，24（7）：773-785.

［14］ADLER A，ARNOLD J H，BAYFORD R，et al.GREIT：a unified approach to 2D linear EIT reconstruction of lung images［J］.Physiological Measurement，2009，30（6）：S35-S55.

Research on brain electrical impedance tomography method

based on single electrode excitation mode

Wang Meng¹， Zheng Shuo¹， Shi Yanyan^1，2， Liao Juanjuan¹

（1. College of Electronic and Electrical Engineering， Henan Normal University， Xinxiang 453007， China;

2. School of Biomedical Engineering， Fourth Military Medical University， Xi′an 710032， China）

Abstract： As a new visualization technology， electrical impedance tomography（EIT）can reconstruct the conductivity distribution of human tissues according to pathological changes， providing a choice for disease detection. While detecting brain disease basing on EIT， to improve the sensitivity distribution of the measured area and solve the typical ill-posed problem in electrical impedance tomography， a single electrode excitation data acquisition mode is adopted in this paper， a k-order finite-difference L₁regularization objective function is proposed， and the augmented Lagrange and alternating direction algorithms are used to solve the objective function to reconstruct the conductivity distribution. The influence of external resistance on the sensitive field under single electrode excitation mode is researched. For intracerebral hemorrhage and intracerebral ischemia， the image reconstruction performance of Landweber method， Newton-Raphson method， Tikhonov， total generalized variation method and the proposed method are compared. The results show that ALAD-LR method with single electrode excitation mode can effectively improve the quality of image reconstruction and has strong robustness in the image reconstruction of cerebral hemorrhage and cerebral ischemia.

Keywords： electrical impedance tomography; image reconstruction; single electrode excitation; regularization method

［責(zé)任編校 楊浦 劉洋］