協方差矩陣分解的CNN協作頻譜感知

師浩東,姜 斌,包建榮,劉 超

(杭州電子科技大學通信工程學院,浙江 杭州 310018)

0 引 言

隨著互聯網時代的到來,萬物互聯的時代將帶來幾何級增長的數據,現階段可使用的頻譜資源已不能滿足用戶的日益需求,所以除了尋找更高通信頻段,采用動態頻譜共享模式以及靈活的頻譜資源配置,將會是未來通信技術發展的一個重要方向。認知無線電(Cognitive Radio, CR)技術作為緩解頻譜資源稀缺的關鍵技術之一,其主要目的是讓無線通信系統擁有從周圍環境學習的能力,可以實時互換信息,檢測并使用可用的空閑頻譜。安全可靠的頻譜感知是CR系統正常工作的前提,是頻譜共享得以實現的重要環節。單節點頻譜感知主要包括了能量檢測(Energy Detection, ED)、匹配濾波器(Matched Filter, MF)檢測、循環平穩特征(Cyclostationary Feature, CF)檢測等[1]。其中,ED復雜度較低,但在低信噪比下無法區分主用戶信號和噪聲[2]。MF檢測時間短、精度高,但對主用戶先驗信息要求較高[3]。CF在低信噪比下檢測率高,但復雜度高,延遲較大[4]。針對噪聲帶來的影響,文獻[5]用樣本特征之差來減少噪聲波動帶來的影響,文獻[6]提出了基于進化博弈論的協作頻譜方法,降低了噪聲影響,并提高了吞吐量,但其檢測閾值及性能都不穩定。文獻[7]采用人工蜂群優化,完成了噪聲不確定下的協作頻譜感知,但其協作頻譜感知中檢測門限不易確定。文獻[8]將支持向量機(Support Vector Machine, SVM)用于頻譜感知方法,通過對接收信號預處理后組成的特征向量,最終獲得較好分類效果。但其訓練時間長,特征參數提取不足。文獻[9]在信號分類引入了卷積神經網絡(Convolutional Neural Network, CNN),取得了較高識別率。但其未構造特征參數,致使頻譜檢測效果還有改進余地。

故針對上述檢測閾值不穩定、低信噪比下識別率低等問題,采用Cholesky分解及統計量構造、CNN分類等方法,提出了協方差矩陣分解的CNN協作頻譜感知方案,具有特征參數提取充分、檢測時間短、低信噪比下檢測精度高等優勢。

1 CNN協方差矩陣分解的協作頻譜感知

1.1 頻譜感知系統模型

認知無線系統常包含1個主用戶(primary user, PU),M個次用戶(secondary user, SU)。在頻譜檢測中,認知基站(cognitive base station, CBS)先對PU檢測,判斷PU狀況并確定空閑頻譜。然后,發送接收機(PU-receiver,PU-R)狀態,確定空閑頻譜。當PU-R在檢測區域時,繼續檢測。否則,釋放之前頻譜后,SU才可利用。若PU訪問SU使用的頻段時,則SU退出。并檢測其它空閑頻段。

當PU通信未被干擾時,第i個次用戶SUi對PU信號檢測,接收信號采用二元假設模型表示為:

(1)

其中,ri(k)表示第i個次用戶在時刻k所接收的連續時間序列,hi(k)為表示在時刻k第i個傳輸信道損耗系數;s(k)表示PU的信號,ni(k)表示均值為0、方差為σ2的加性高斯白噪聲;H0表示不存在PU信號,H1表示存在PU信號。

1.2 數據預處理

設SU有L根天線,次用戶在k時刻接收到L個連續時間序列,接收到的信號通過采樣后得到L×N維矩陣Rk,然后求出其協方差矩陣為N×N維的矩陣SN。然后,將其通過Cholesky法分解,得

SN=XXT,其中X為下三角矩陣,表達式為:

(2)

其中,N為采樣點數,Xi,j≥0,i與j都為整數,計算的表達式為:

(3)

其中,Si,j代表矩陣SN的第i行,第j列元素。

在H0條件下,矩陣X對角元素基本相同,其它元素趨近于0。但在H1條件下,矩陣X對角線元素不同,其它元素值相對較大。故將矩陣X全部元素之和與斜對角線元素之和的比值為統計量為:

(4)

其中,Tk表示每個次用戶產生的第k個統計量,每個次用戶產生的特征向量為:Tk=[T1T2…Tk]T,M個次用戶產生的特征向量構成的特征矩陣為:

(5)

其中,TMk表示第M個次用戶產生的第k個統計量;將TMk歸一化后作為CNN頻譜感知的數據集。

1.3 CNN頻譜感知

本文CNN采用3個卷積層、2個池化層、1個全連接層,如下圖所示。

圖1 CNN結構圖

(6)

其中,w表示權值,b表示偏置值,是CNN反向傳播時不斷優化的參數,lw,b表示訓練數據經過CNN后的映射標簽。

在梯度下降優化方面,采用Adam(Adaptive Moment Estimation)優化器算法,主要是通過梯度的一階矩估計和二階矩估計來調制每個參數的學習率,更新過程為:

(7)

該算法計算m時有momentum加速下降的屬性,計算v時有adagrad阻力的屬性,更新參數時把m和v都考慮進去,計算效率高。

1.4 算法流程設計

算法分為數據預處理和CNN頻譜感知兩部分,流程圖及步驟如下:

步驟1：對SU接收信號N次采樣,得到L×N維矩陣,求出其協方差矩陣,之后通過Cholesky法分解得到下三角矩陣X;

步驟2：將X的全部元素之和與斜對角線元素之和的比值作為統計量,然后M個次用戶產生的統計量組成一個統計矩陣,作為單個訓練樣本;

步驟3：按照步驟1和步驟2,在不同信噪比下,分別產生H0和H1條件下的樣本,分別用“0”和“1”標記后,在不同梯度下降優化算法下,設置不同的epoch和batch,通過CNN訓練訓練集,選擇accuracy最高并且loss最低的優化器,確定系統模型參數,再通過測試集測試得到檢測結果。

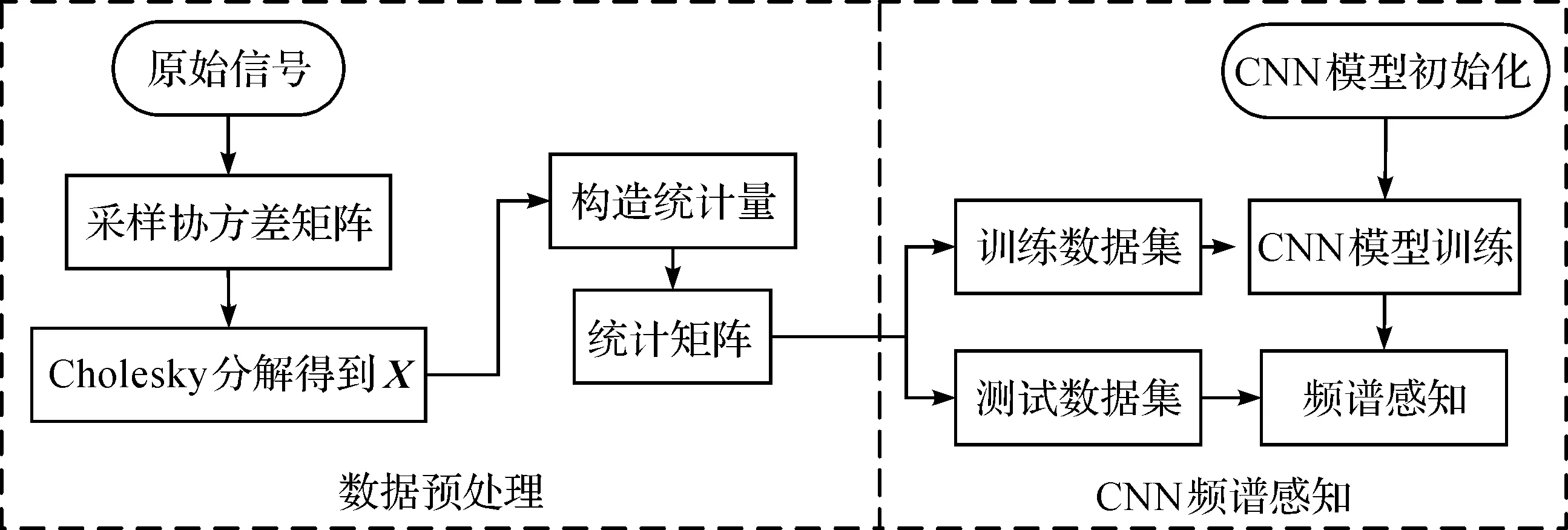
圖2 CNN協方差矩陣分解的協作頻譜感知算法流程圖

2 算法性能對比與分析

2.1 實驗數據準備

本次實驗數據集均在Matlab 2018平臺上仿真產生,用于訓練與測試的CNN框架是基于Python3.8環境下的Tensorflow-2.3.0深度學習框架。主用戶信號采用BPSK信號,噪聲采用均值為0、方差為1的高斯白噪聲,次用戶數M固定為10個,天線L為10根,采樣點數N為100。

2.2 CNN頻譜感知模型訓練精度

訓練次數epoch設為100,batch設為100個,圖3為在不同優化算法下的訓練精度。

圖3 不同優化算法下的訓練精度及損失值

由圖3得,訓練過程中accuracy值整體穩步上升,Adam優化性能最佳,該優化器在訓練次數達到60次時,accuracy值穩定在約100%,loss值基本穩定在0左右。原因如下:Adam本質是momentum和RMSprop的結合,經偏置校正后,每次迭代學習率都有確定的范圍,使參數較平穩;而且,式(8)中的m和v都得到更新,計算效率高,適合非靜態目標和稀疏梯度的問題,為不同參數計算不同自適應學習率,適合大數據集和高維空間,故Adam學習算法優于其它算法。

2.3 算法性能比較及分析

圖4左邊為6種算法在虛警概率Pfa=0.1時,檢測概率Pd對比圖,SNR取值范圍為:-20 dB～0 dB;右側是SNR為-13 dB時,6種算法的接收者操作特征(Receiver Operating Characteristic, ROC)曲線圖。

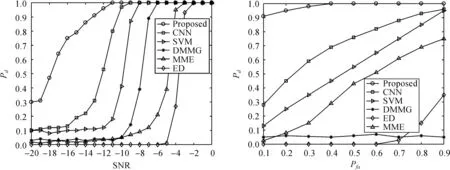
圖4 各算法的檢測概率及ROC曲線

由圖4可得,當SNR為-15 dB時,本算法Pd比傳統CNN和SVM各高約60%和69%。其原因如下:SVM是對協方差矩陣的特征值檢測,雖然解決了閾值不精確問題,但未充分利用其攜帶的所有信息。CNN模型在處理高維矩陣方面比SVM更具優勢,故CNN檢測概率整體高于SVM。其次,與傳統CNN相比,所提方案通過式(3)的Cholesky分解和與式(6)的統計量計算,將PU與噪聲信號的特征提取出來,增強了PU信號的影響,達到更好的分類效果。

3 結束語

本文主要提出了一種CNN協方差分解的協作頻譜感知算法,具有低信噪比下檢測精度高、時間短等性能。其優勢如下:對信號協方差矩陣Cholesky分解后構建統計量,可降低噪聲干擾;對多個次用戶統計量融合,提高協作性并減少誤差;通過CNN信號分類,自主學習確定決策閾值,可提高其精度。因此,所提方案的檢測精度可獲得顯著提高,適用于5G時代下復雜的多噪聲環境。