基于ISOA的微織構機床伺服前饋補償控制

王忠明，吳國慶，茅靖峰，胡 坤

（南通大學電氣工程學院，江蘇 南通 226019）

1 引言

為了進一步滿足現代機床加工業的技術需求，機床加工必然朝著高速化和精密化方向發展。微織構機床憑借其可以精確的加工出復雜微觀形貌結構，并滿足快速定位系統的技術要求，因此被廣泛應用于機床加工領域。伺服系統和滾珠絲杠進給系統構成了微織構機床伺服進給系統，而伺服系統的性能影響著微織構機床的速度跟蹤精度[1-3]。在設計伺服系統的進程中，PID控制器憑借其適用性強和簡單易實現的特點，廣泛應用于實際使用中[4]。然而PID參數整定困難成為科研一大難點，隨著智能算法研究的不斷深入，人們開始將其應用于PID參數尋優中。文獻[5]為了解決系統階躍響應超調以及振蕩的問題，提出使用人群搜索優化算法進行參數整定，提高系統的控制精度；文獻[6]針對微織構機床位置跟蹤精度不高的問題，建立微織構機床伺服傳動系統數學模型，采用前饋與反饋結合的改進方法，提高了機床的位置跟蹤精度；文獻[7]針對水泵系統控制精度不高的問題，使用人群搜索優化算法獲得良好的PID參數自整定效果，提高了灌溉系統的運行穩定性。

綜上所述，為了進一步提高微織構機床速度伺服跟蹤精度，在建立機電耦合動力學模型的基礎上，提出基于改進人群搜索優化算法的前饋PID 控制策略，實現微織構機床伺服進給系統的PID參數尋優設計。為驗證該控制策略的實際效果，采用Matlab搭建仿真實驗平臺，與傳統智能優化算法相比較。仿真結果表明，基于ISOA優化的前饋補償PID優化效果更好，速度跟蹤性能得到很大改善，驗證了其正確有效性。

2 微織構機床伺服進給系統建模

2.1 交流永磁同步電機數學模型

永磁同步電機假設為理想電機：渦流損耗被忽略；永磁體也無阻尼作用；電機阻尼繞組等效于d、q軸上兩個短路的阻尼繞組。建立坐標的等效變換，根據矢量控制原理，進而得到d-q坐標系數學模型[8]，其矢量圖模型，如圖1所示。

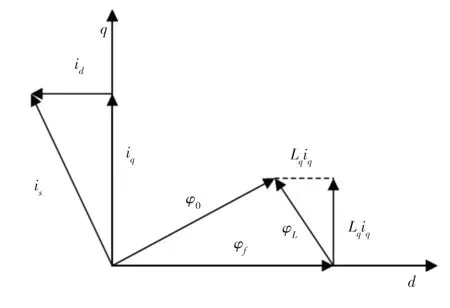
圖1 永磁同步電機矢量圖Fig.1 Permanent Magnet Synchronous Motor Vector

由圖1可得出其d-q軸上電壓平衡方程式為：

式中：R—等效電阻值；Lq=Ld—dq軸電感；ωr—電機輸出軸轉子角速度；id、iq—dq軸電流；ud、uq—dq軸電壓；pn—磁極對數；φf—永磁體上恒定磁通。

根據式（1）可推導出PMSM的電流方程為：

PMSM的電磁轉矩Te為[9]：

2.2 滾珠絲杠進給系統建模

滾珠絲杠與伺服電機通過聯軸器相連在一起，滾珠絲杠通過兩端的軸承支撐，工作臺由滾珠絲杠螺母旋轉驅動，沿著直線導軌副做直線往復運動，光柵尺作為負反饋裝置，構成系統全閉環，其模型[10]，如圖2所示。

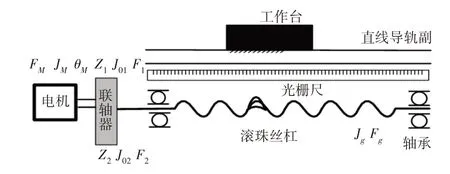
圖2 滾珠絲杠進給機構模型Fig.2 Ball Screw Feed Mechanism Model

式中：TL—擾動；J—轉動慣量之和，可由等效轉動慣量Jo1、Jo2、絲杠轉動慣量Jg和電機軸轉動慣量JM求出；F—總的阻尼系數，可由電機軸的阻尼FM、滾珠絲杠阻尼Fg和絲杠與電機間等效阻尼F1、F2求出；Z1∕Z2—折算比。

2.3 機電耦合動力學模型

在假設理想電機的條件下，使Ld=Lq=L，FM=0，為了實現快速調速，采用id=0方法用于控制PMSM調速系統定子電流解耦，完全解耦的微織構機床伺服進給系統狀態方程為：

根據式（5）的狀態方程，微織構機床伺服進給系統框圖可描述，如圖3所示。

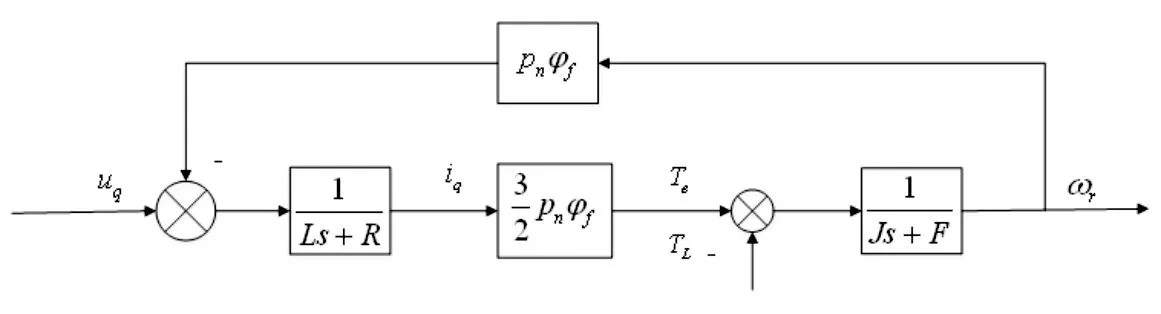
圖3 微織構機床伺服進給系統框圖Fig.3 Block Diagram of the Servo Feed System for Micro-Texture Machine Tools

根據圖3，微織構機床伺服進給系統傳遞函數GM(s)為：

3 進給系統線性控制器設計

3.1 PID控制

微織構機床伺服進給系統所采用的傳統PID控制器，主要是對三個環節參數Ki、Kp、Kd整定，PID控制器框圖，如圖4所示。

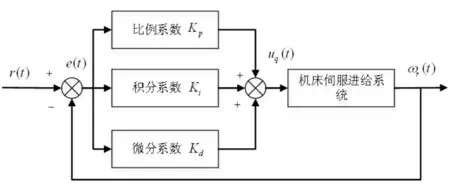
圖4 PID控制器框圖Fig.4 PID Controller Block Diagram

其控制規律表示為：

式中：e(t)—速度跟蹤誤差；Ti、Td—積分時間常數和微分時間常數。

3.2 前饋補償控制器設計

考慮到傳統PID控制的反饋控制環節存在延時問題，這些問題會造成控制滯后甚至失效，因此提出前饋補償的PID 控制方式。其原理框圖，如圖5所示。

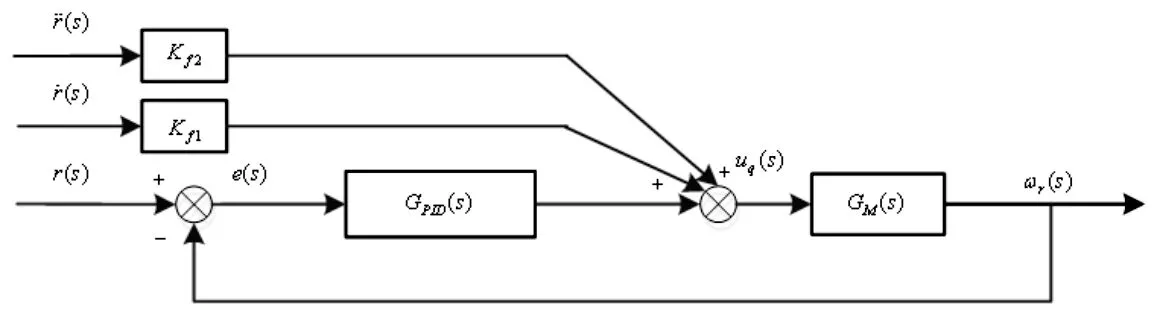
圖5 前饋PID控制器框圖Fig.5 Feedforward PID Controller Block Diagram

系統傳遞函數ωr(s)∕r(s)和系統誤差關于輸入的傳遞函數e(s)∕r(s)為：

式中：r(s)—初始輸入的信號；uq(s)—拉氏變換下的電壓輸入；GPID(s)—拉氏變換下PID傳遞函數；e(s)—拉氏變換下的速度跟蹤誤差；Kf1、Kf2—前饋增益系數。

由上式得可知，當f1(s)+f2(s)=1∕GM(s)時，理論上可消除系統誤差。盡管在實際使用中無法完全消除系統誤差，但可以將其降低到可接受的水平，盡可能不影響系統穩定性的前提下，機床速度伺服跟蹤精度得到很大提升。

對于PID采樣周期Tc較短的情況，可通過PID離散化處理，直接將連續系統轉換離散系統，因此前饋補償PID離散控制律可表示為：

式中：e(k)—速度跟蹤誤差。

對于一個存在非線性和滯后性的微織構機床伺服進給系統，結構簡單易實現的PID控制器調參困難成為難題，因此采用改進的人群搜索優化算法的PID參數自整定，來實現系統全局最優控制。

4 人群搜索算法及其改進

4.1 PID控制

人群搜索算法[11]是一種新型人類種群行為的智能算法，把搜索行為的集和當作初始種群，行為個體作為個體解，對位置和方向推理判斷是通過人類在進行搜索時的模擬，實現所求問題的最優求解。

使用時間積分的絕對值來構造目標函數，以期得到合適的動態迭代特性，構造的目標函數f為：

人群搜索優化算法遵循人群搜索規則，利用Fuzzy系統的逼近功能，可得到搜索步長αfj關系式為：

式中：ψfj—隸屬度函數的參數；

?fj—搜索空間目標函數的隸屬度。

通過對預動方向de、利他方向da和利己方向dp的理性分析，得出搜索方向df為：

式中：sign()—符號函數；m1、m2—[0，1] 區間隨機實數。

得到搜索步長αfj和搜索方向df后，再進行個體位置更新，得到更新后的位置xfj(t+1)為：

4.2 改進的SOA算法

為了解決人群搜索算法在前期搜索效率低以及后期搜索陷入局部極值而無法求出全局最優解的問題[12]，提出了混沌初始化優化策略，并且引入cauchy變異算子，Logistic混沌映射函數反復迭代[13-14]：

模擬試塊注漿試驗結束后，在頂面位置和側面位置各取一組芯樣(6塊)，并對其芯樣進行抗壓試驗。由于試驗1的注漿固結效果較差，漿液擴散不均勻導致脫模后完整性差，無法取芯，故只對試驗2—試驗4進行取芯和單軸抗壓強度試驗。代表性試樣及單軸壓縮試驗見圖5，不同模擬試驗方案下的試樣取樣部位及其單軸抗壓強度值見表2。

式中：Φ—迭代次數；μ—調節參數。

在(0，1) 區間內隨機產生一個H維的基準粒子y0，y0=(y01，y02，y03···y0H)，產生混沌種群集合yn+1，j為：

接著將式(0，1) 映射到搜尋空間[-Γ，Γ]中，得到H維粒子種群xn+1，j為：

式中：n=0，1，2，···，N，j=1，2，···，H。

為了解決搜索后期陷入局部極值的現象，引入cauchy變異算子，柯西分布的主要表現為其分布函數擁有較長的兩翼，其生成的隨機數的變異范圍更廣，因此柯西變異算子增大的變異范圍使改進算法擁有更廣的搜索范圍。

柯西變異的計算公式為［15-16］：

式中：p—隨機變異率；

cauchy()—準柯西分布函數。

接著使用柯西分布對Gbest執行變異操作為：

式中：r—變異權重；Gbestj—全局最優第j維分量；λ—常數10；A()—柯西分布最初產生的隨機數。

5 基于ISOA算法的前饋控制器設計

5.1 ISOA-PID控制器原理圖

利用基于ISOA的前饋補償PID控制策略，對輸出速度跟蹤值及其誤差值分別進行優化處理，調節控制器的三個參數Kp、Ki、Kd，提高速度跟蹤精度，消除速度跟蹤誤差，到其控制系統原理，如圖6所示。

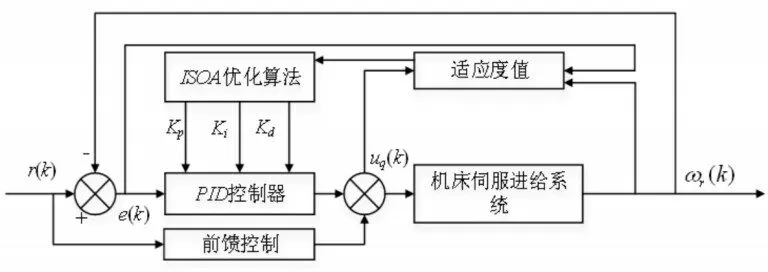
圖6 控制系統原理框圖Fig.6 Block Diagram of the Control System

5.2 ISOA-PID的算法流程

ISOA優化PID參數流程圖，如圖7所示。

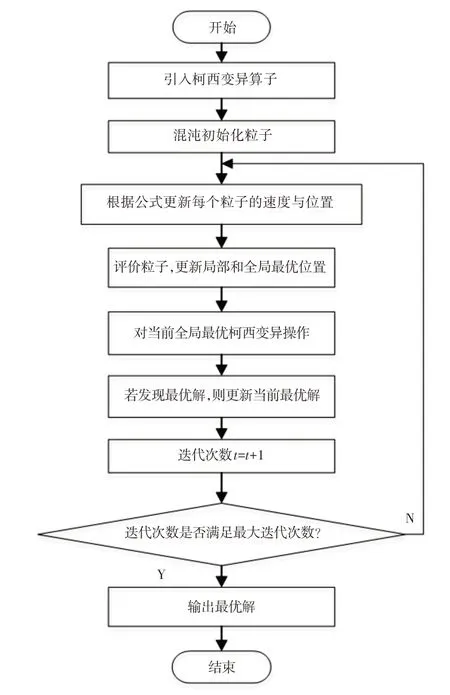
圖7 ISOA優化PID參數流程圖Fig.7 Flow Chart of ISOA Optimization PID Parameters

6 仿真測試與結果分析

為了驗證ISOA+前饋PID算法的正確有效性，設計耦合模型參數，得出微織構機床伺服進給系統傳遞函數，基于MATLAB仿真與人群搜索優化（SOA）、粒子群優化算法（PSO）和遺傳優化算法（GA）進行結果對比。建模所需參數，如表1所示。

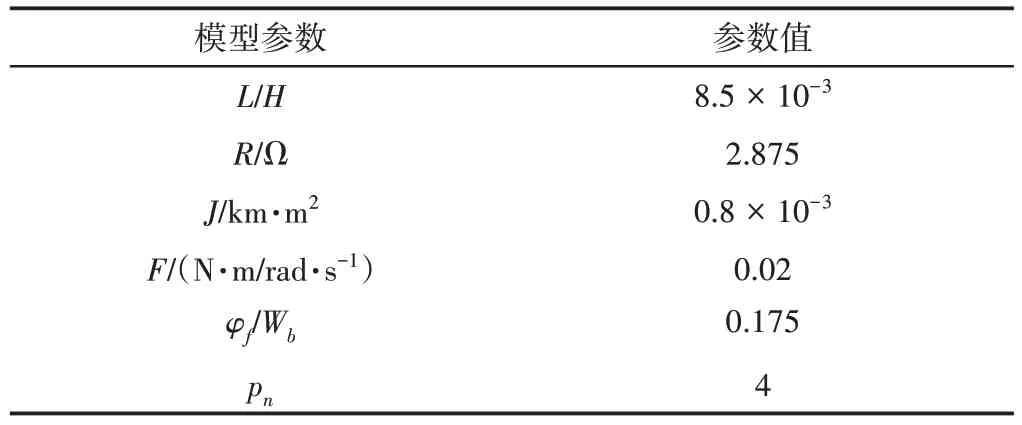
表1 機電耦合模型參數Tab.1 Parameters of Electromechanical Coupling Model

微織構機床伺服進給系統傳遞函數為：

針對微織構機床伺服進給系統數學模型進行仿真研究，分別編寫基于ISOA、SOA、PSO和GA優化算法程序，設置起始種群為30，維數為3，采樣周期為1ms，最大迭代次數為100代，隸屬度最小值為0.0111，隸屬度峰值為0.9500，最小權重值為0.1，權重峰值為0.9，四種優化算法仿真Kp、Ki、Kd參數，如表2所示。仿真得到SOA、GA、ISOA和PSO控制適應度值函數控制構制曲線，如圖8所示。四種算法的迭代次數和最優適應度值，如表3所示。

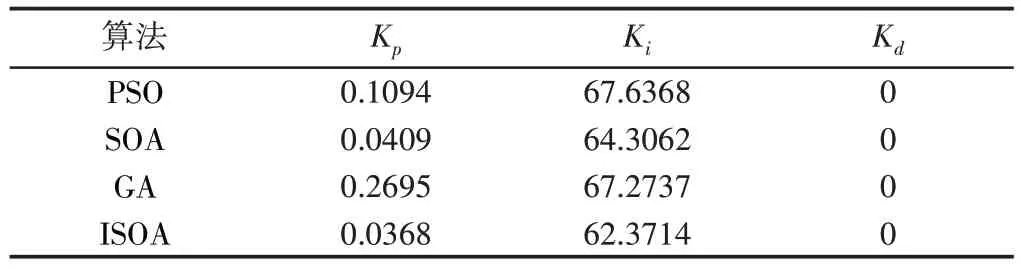
表2 四種優化算法仿真Kp、Ki和Kd參數Tab.2 Four Kinds of Optimization Algorithm Simulation Kp、Ki and Kd Parameters

表3 四種算法的迭代次數與最優適應度表Tab.3 The Number of Iterations and Optimal Fitness of the Algorithms

圖8 適應度函數控制曲線Fig.8 Fitness Function Control Curve

PSO優化算法經過3次迭代獲得的最優適應度值最差且為5.3×10-3，SOA優化算法經過10次迭代獲得其適應度函數的最優適應度為4.9742×10-4，GA優化算法經過21次迭代找到的最優適應度為7.6817×10-5，而ISOA 優化算法找到的最優適應度為1.3618×10-6，且僅需要12次迭代。由此可見，四種優化算法相比較，PSO優化算法穩定性最差，而ISOA優化算法在尋找最優適應度值速度最快且最穩定,如表2、圖8所示。

將式(19)作為仿真的基礎，輸入為r=0.5 sin(2πt)的正弦加速度信號，接著使用6種算法仿真，正弦響應速度跟蹤曲線，如圖9所示。正弦響應速度跟蹤誤差曲線，如圖10所示。分別將正弦響應速度跟蹤曲線和正弦響應速度跟蹤誤差曲線進行局放大，使改進方法與傳統優化算法的比對能更清楚直觀的表達，正弦響應速度跟蹤曲線部分放大圖，如圖11所示。正弦響應速度跟蹤誤差曲線部分放大圖，如圖12、圖13所示。

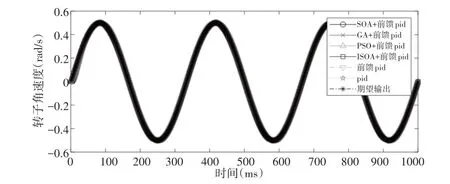
圖9 正弦響應速度跟蹤曲線Fig.9 Sinusoidal Response Speed Tracking Curve

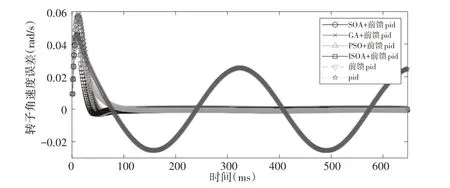
圖10 正弦響應速度跟蹤誤差曲線Fig.10 Sine Response Velocity Tracking Error Curve

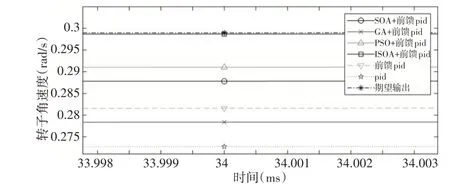
圖11 正弦響應速度跟蹤曲線部分放大圖Fig.11 Partial Enlarged View of the Sine Response Speed Tracking Curve

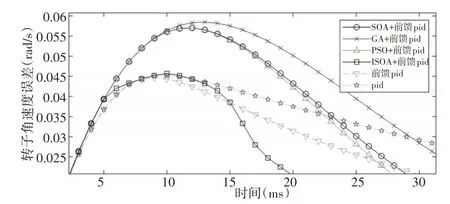
圖12 正弦響應速度跟蹤誤差曲線部分放大圖Fig.12 Partial Enlarged View of Sine Response Velocity Tracking Error Curve

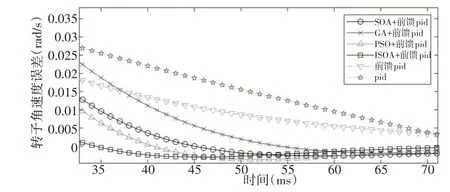
圖13 正弦響應速度跟蹤誤差曲線部分放大圖Fig.13 Partial Enlarged View of Sine Response Velocity Tracking Error Curve

由圖11可知，6種算法中，ISOA+前饋補償PID 速度伺服跟蹤效果最佳，跟蹤精度較高，而常規PID跟蹤精度最差。由圖12所知，在6種算法中，GA+前饋PID誤差峰值最大且為0.058rad∕s，而ISOA+前饋PID 誤差峰值最小且為0.046rad∕s。由圖13所示，ISOA+前饋補償PID 方法調節最快，0.06s 達到穩定狀態，其次PSO+前饋補償PID方法0.08s達到穩態，其他算法速度跟蹤性能略差。綜上所述，對于大多數非線性帶有遲滯環節系統，微織構機床伺服運動控制系統基于ISOA優化的前饋補償PID控制效果最優。

7 結論

（1）基于ISOA算法優化的前饋補償PID控制在微織構機床伺服進給控制中調節時間最短，速度伺服跟蹤精確，動態響應特性較好，通過該改進方法可以實現微織構機床伺服進給系統中的最佳控制策略。

（2）在ISOA 算法的使用過程中，調整其適應度函數值和粒子種群的大小能夠改善PID參數優化效果，很大程度消除PID控制器在微織構機床伺服進給系統中存在的非線性、時變性和滯后性問題；前饋補償作為延時系統中常用的模型控制方法，該方法在盡可能不影響系統穩定性的前提下，獲得更好的動態特性和更高的控制精度。

（3）仿真結果表明，基于ISOA 的微織構機床前饋伺服控制可以很好的滿足機床伺服進給系統的自動控制要求，可應用于實際工業機床控制中。