控制開放超導量子電路系統中的 幾何量子關聯凍結和量子相干性

吳春艷 宋曉書 呂兵 賀啟亮

本文研究了開放超導量子電路系統中， 含時電磁場對兩超導量子比特間的幾何量子關聯和量子相干性的影響. 我們發現， 加入磁場之后， 幾何量子關聯被凍結的現象會出現， 并且凍結的時間會隨著含時電磁場的加入而得到延長. 利用跡距離的方法， 我們探討了含時電磁場對超導量子比特與環境之間量子信息流動的影響， 我們發現含時電磁場可以抑制環境的影響， 降低超導量子比特與環境之間的量子信息流動.

開放超導量子電路系統； 幾何量子關聯； 量子相干性； 含時電磁場

O431.2 A 2024.014003

Control of the frozen geometric quantum correlation and quantum ?coherence in dissipative superconducting quantum circuit

WU Chun-Yan， SONG Xiao-Shu， L Bing， HE Qi-Liang

（School of Physics and Electronics， Guizhou Normal University， Guiyang 550001， China）

We investigate the influence of time-dependent electromagnetic field on the geometric quantum correlation and quantum coherence between two superconducting qubits in an open superconducting quantum circuit system. It is shown that the freezing of geometric quantum correlation will occur after the addition of magnetic field， and the freezing time will be extended with the addition of time-dependent electromagnetic field. In addition， the influence of time-dependent electromagnetic field on the quantum information flow between superconducting qubits and the environment is discussed by using trace distance method. It is found that the time-dependent electromagnetic fields can suppress the effect of the environment and slow down the exchange of the quantum information flows between the superconducting qubits and the environment.

Open superconducting quantum circuit system；Geometric quantum correlation；Quantum coherence；Time-dependent electromagnetic field

1 引 言

近年來， 隨著宏觀固態物理實驗的快速發展， 基于約瑟夫遜結的超導電路系統已經成為了理論和實驗研究的熱點， 引起了人們的廣泛關注 ?［1-5］ . 超導電路系統具備許多天然原子所不具備的有趣性質， 這使其成為了量子信息和量子計算領域的很有前途的候選者之一. 在實驗上， 超導量子比特系統已經展示了其具有宏觀的量子相干性和可集成性， 并且可在一定的條件下實現雙量子位門和量子混合系統 ?［6-8］ . 正是由于超導量子比特系統所具有的可控性和集成性， 一些研究人員提出， 具有公共數據總線的耦合超導量子比特系統可以用于實現較為復雜的量子信息任務 ?［9-11］ .

另一方面， 穩定的量子資源對量子信息任務的有效執行是至關重要的. 然而， 一個真正的量子系統會不可避免地與周圍環境發生相互作用從而導致退相干. 退相干的發生也意味著開放系統中包含的量子關聯將因環境擾動和量子波動而消失. 所以， 退相干成為量子信息任務有效執行中最大的挑戰之一. 近年來， 人們對于開放系統的量子關聯研究越來越有興趣. 各種退相干通道中的量子關聯的變化行為的研究， 可能有助于我們實現現實世界中的量子信息任務 ??［12，13］ . 此外， 許多研究者致力于尋找不同的方法來控制退相干動力學 ?［14-16］ 以及產生穩態量子關聯 ?［17-20］ 的方案.

如上所述， 國內外研究者在幾何量子關聯度量 ?［21-23］ 、開放系統中量子相干性特性研究 ?［24-27］ 以及基于超導量子電路系統的量子信息任務實現 ?［28-30］ 等方面都開展了許多研究工作， 但是對于利用含時電磁場在開放超導量子電路系統中延長幾何量子關聯被凍結時間， 以及增大系統中超導量子比特間的量子相干性還未見相關報道. 基于此， 本文針對開放超導量子電路系統， 研究了利用含時電磁場延長幾何量子關聯被凍結時間， 以及增大系統中超導量子比特間量子相干性的可能.

首先， 基于開放環境下系統隨時間演化的馬爾科夫主方程， 本文運用超算符計算方法， 獲得了兩超導量子比特隨時間演化的約化密度矩陣， 同時根據幾何量子關聯的度量方法， 分析和對比了系統參數以及含時電磁場對兩超導量子比特間幾何量子關聯的影響. 研究表明， 系統中出現了幾何量子關聯被凍結的現象， 并且被凍結的時間隨著LC電路初始相干態參數的增大而減小. 而且當加入含時電磁場后， 系統中幾何量子關聯被凍結的時間增加. 其次， 利用相對熵量子相干性， 探討了超導量子比特間量子相干性隨含時電磁場參數的變化. 研究發現隨著含時電磁場強度的增加， 超導量子比特間量子相干性衰減的速率減小， 穩態量子相干性提高. 最后， 借助跡距離的方法， 分析和討論了含時電磁場對開放超導量子電路系統與環境之間量子信息流動的影響. 結果顯示， 含時電磁場可以抑制超導量子比特與環境之間的量子信息流動， 降低環境對超導量子電路系統的影響， 從而保護超導量子電路系統初始具有的量子性質.

2 ??含時電磁場對開放超導量子電路系統幾何量子關聯突然轉變的影響

本節分析了加入含時電磁場后超導量子電路系統中兩超導比特之間幾何量子關聯的變化. 幾何量子關聯是基于Schatten 1-范數 ?［23］ 的量子discord的幾何度量來進行定義的， 對于兩體系統 ρ ?ab ?（其中 a 和 b 分別代表兩個子系統）， 1-范數幾何量子關聯可以用量子態 ρ ?ab ?與離它的最近的經典量子態 ρ c ?ab ?之間的跡距離來進行定義 ?［22，23］ ， 其表達式可以寫為：

D（ρ ?ab ）= ?min ???ρ c ?ab ∈ρ 0 ?‖ρ ?ab -ρ c ?ab ‖ 1 ?（1）

而其在子系統 a 上進行局域測量之后的經典關聯可以表示為 ?［22，23］ ：

C= ?max ???ρ c ?ab ∈ρ 0 ?‖ρ c ?ab -π ?ab ‖ 1 ?（2）

式中， ?ρ 0 表示局部測量下量子discord為零的經典量子態; ?π ?ab ?是單體部分的量子態直積形式; ??‖M‖ 1= Tr（ M +M ） 表示Schatten1-范數. 一般來說， 與量子態 ρ ?ab ?對應的經典量子態 ρ c ?ab ?形式可以表示為 ρ ?c ?ab =∑ ???j|ξ ?j> ?a<ξ ?j| ρ ?b（j） .

開放超導量子電路系統是由兩個超導量子比特與一個共同的耗散數據總線進行耦合構成的. 這里的數據總線是由 LC 電路組成. 含時電磁場驅動超導量子比特. 超導量子比特與 LC 電路之間的相互作用已經在實驗上被證實 ?［2］ . 整個系統的哈密頓量可以寫為 ?［3］ （如圖1所示， 設 ?=1）：

H 0=ωa +a+∑ ?j=a，b ??ω 0 2 （σ ?z j+g 0aσ ?+ j+ ?λ 0e ??-iω ct σ ?+ j）+h.c. ?（3）

這里， 算符 σ + j=|e> j j j j j 和 |e> j 是第 j 個超導量子比特的基態與激發態; ?ω=1/ LC ?是 LC 電路的頻率; ?ω c 是含時電磁場的頻率; ?ω 0 是超導量子比特的頻率， 其表達式為：

ω 0= 1 2 ?J 2 0 （Φ ?e - Φ 0 2 ） ?2+T 2 ?RL ???（4）

此處， ?Φ ?e是bias flux， ?J 0 是環路電流， 參數 T ?RL ?指的是超導比特兩個勢阱之間的隧道耦合強度 ?［31］ . ?a ?和 a 是 LC 電路的升降算符， 被定義為 ?［3］

a = Cω φ+i ?1 Cω ?Q ， ?a= Cω φ-i ?1 Cω ?Q ?（5）

φ 是通過 LC 電路的磁通量， ?Q 是 LC 電路電容 C 的存儲電荷， ?L 是 LC 電路的自感. 磁通量 φ 和電荷 Q 滿足對易關系 ?Q，φ =i . ?λ 0 是含時電磁場與超導比特之間的相互作用強度， ?g 0 是超導比特與 LC 電路之間的耦合強度， 可以表示為

g 0=M ?ω 2L ?〈e J 0 g〉 ?（6）

M 是超導量子比特與 LC 電路耦合的互感.

利用文獻［3］中相同的方法， 在墜飾態表象下并考慮dispersive極限 ?［32］ ， 哈密頓量 H 0 可以被重新寫成

H T= Ω ?{∑ ?j=a，b ?（ |+〉 ??j〈+|aa +- |-〉 ??j〈-|a +a）+ ??（σ ～ ?+ ?aσ ～ ??- b+σ ～ ??- aσ ～ ??+ b} ?（7）

其中， ???|+〉 ?j= cos η |e〉 ?j+ sin η |g〉 ?j ， ??|-〉 ?j=- sin η |e〉 ?j+ cos η |g〉 ?j 表示第 j 個量子比特的墜飾態， ?σ ～ ?+ j=|+> j<-| ， ?σ ～ ?- j=|-> j<+| ， ???Ω ?= g 0 ?cos ??2η ?Δ 2+4λ 2 +ω c-ω ?， ??tan η= 2λ ω 0-ω c ?， ?Δ=ω 0-ω c .

考慮超導電路系統與環境發生相互作用， 也就是存在耗散， 其隨時間演化的動力學方程可以利用主方程來進行表示， 即

d ρ（t） ?d t =-i H ?T ，ρ（t） +γ（2aρ（t）a - ?a aρ（t）-ρ（t）a a） ?（8）

假設初始時兩超導量子比特被制備在Bell對角態， ?LC 電路被制備在相干態， 則整個超導系統的初始狀態可以寫為

ρ（0）= 1 4 （I I+∑ 3 ?j=1 ?c ?jσ ?j σ ?j） |α><α| ??（9）

其中 ?c j ∈［0，1］ . 利用超算符方法 ?［33-35］ 并將（9）式代入， 可以求解主方程（8）， 在將 LC 電路求跡約化之后我們可以得到兩超導量子比特的約化密度矩陣.

ρ ??ab （t）= 1 4 （I I+∑ 3 ?j=1 ?c ～ ??j（t）σ ?j σ ?j） ?（10）

這里，

c ～ ??1，2 （t）= 1 2 （c 1+c 2）± 1 2 |c 1-c 2|·|f（t）| 2 ， ???c ～ ?3=c 3 ，

f（t）= exp ?-i Ω ?t+ i|α| 2 Ω ??γ+2i Ω ??（e ?-2（i2 Ω ?+γ）t -1） ??（11）

結合式（1）和式（3）， 我們可以獲得兩量子比特間的幾何量子關聯和經典關聯為 ?［23］

D= median ?c ～ ?1（t），c ～ ?2（t），c ～ ?3（t） ??（12）

C= maximum ?c ～ ?1（t），c ～ ?2（t），c ～ ?3（t） ??（13）

在圖2中， 兩超導量子比特之間的幾何量子關聯和經典關聯被畫為隨時間 t 演化的圖像. 從圖中我們可以看出幾何量子關聯（藍色實線）從初始時間到轉變時間 t ??1 保持不變， 但在該時刻后開始衰減. 這表明從經典退相干到量子退相干的突然轉變現象將在開放超導量子電路系統中出現， 而幾何量子關聯將在轉變時間 t ??1 前保持不變. 從幾何量子關聯對應的方程（12）中可以看出， 如果滿足minimum {c ～ ?1（t）}≤ c 3 ≤ maximum {c ～ ?1（t）} ， 突然轉變現象就會發生. 另外， 通過求解轉變時間滿足的方程

1 2 （c 1+c 2）+ 1 2 |c 1-c 2|·|f（t）| 2=c 3 ?（14）

我們可以得到轉變時間的最大值 t ??max ?=π/4 Ω ??， 從中可以發現最大轉變時間 t ??max ??與有效耦合常數 ?Ω ??成反比關系. 另外， ?LC 電路初始相干態參數 α 對兩超導量子比特間幾何量子關聯的影響被展示在圖3中. 從圖中可以發現， 兩超導量子比特間幾何量子關聯保持不變的時間， 也就是被凍結的時間對于初始相干態參數 α 很敏感， 它將會隨著初始相干態參數 α 的增大而減小. 這說明可以通過減少初始相干態參數 α 來延長幾何量子關聯保持不變的時間.

為了說明含時電磁場對開放超導量子電路系統中幾何量子關聯凍結時間的影響， 圖4展示了在不同強度的含時電磁場下， 幾何量子關聯凍結時間變化的圖像. 從圖中不難看出， 當加入含時電磁場后， 超導量子比特間幾何量子關聯保持常量的時間將會得到延長. 而且當增加含時電磁場的強度， 幾何量子關聯保持常量的時間得到更有效的增加. 這些結果都說明開放超導量子電路系統中幾何量子關聯突然轉變現象可以通過含時電磁場來進行調節， 即可以通過含時電磁場來延長幾何量子關聯突變的時間， 并且含時電磁場強度越大， 延長的效果越好.

3 ?含時電磁場對開放超導量子電路系統量子相干性的影響

本節將利用量子相對熵的方法來研究含時電磁場對于開放超導量子電路系統量子相干性的影響. 2014年， Baumgratz等人 ?［36］ 引入了一個嚴格的量化相干性框架， 并提出了易于計算的量化量子相干性方法. 他們通過固定 d 維希爾伯特空間中的特定基 ?|i〉 ?， 可以將空間中全部非相干態表示為

δ ?^ =∑ d ?i=1 ?p ?i|i〉〈i| ??（15）

并將它們標記為集合 I . ?如果對于所有的 n 條件 K nIK ?nI 都被滿足， 那么量子運算 ρ→∑ ?nK ?nρK ??n 則稱為非相干運算. 根據資源理論， 一個合理的度量量子相干性的計算方法應該滿足以下條件 ?［36］ ：

（1） 如果 ρ∈I ， ?C（ρ）=0 .

（2） 非選擇性非相干完全正定保跡（ICPTP）映射Λ下的單調性： C（ρ）≥C（ Λ ρ） ， 其中 ?Λ ρ=∑ ?nK ?nρK ??n ， ??K ?n ?是一組非相干的Kraus算符， 滿足 ∑ ?nK ?nK ??n=I ， ?K ?nIK ??nI.

（3） 選擇性測量Λ ?n 下的平均單調性： C（ρ）≥∑ ?np ?n Λ ??nρ ， 這里概率 p n= Tr ?K nρK ?n ?.

（4） 在量子態為混合態情況下的凸性， 即非遞增性： ?∑ ?np ?nC（ρ ?n）≥C（∑ ?np ?nρ ?n）.

Baumgratz等人 ?［36］ 提出的相對熵量子相干性、 l 1 范數相干性等都滿足以上條件. 這里我們采用量子相對熵的方法度量超導比特間的量子相干性. 相對熵量子相干性的表達式為 ?［36］

C ??RE ?=S（ρ ??diag ?）-S（ρ） ?（16）

其中， ?S（ρ）=- Trρ log ??2ρ 是密度矩陣 ρ 的馮諾依曼熵； ρ ??diag 是將 ρ 的所有非對角元素刪除之后得到的對角密度矩陣. 根據（10）式和（16）式， 我們可以獲得兩超導量子比特間量子相干性的表達式.

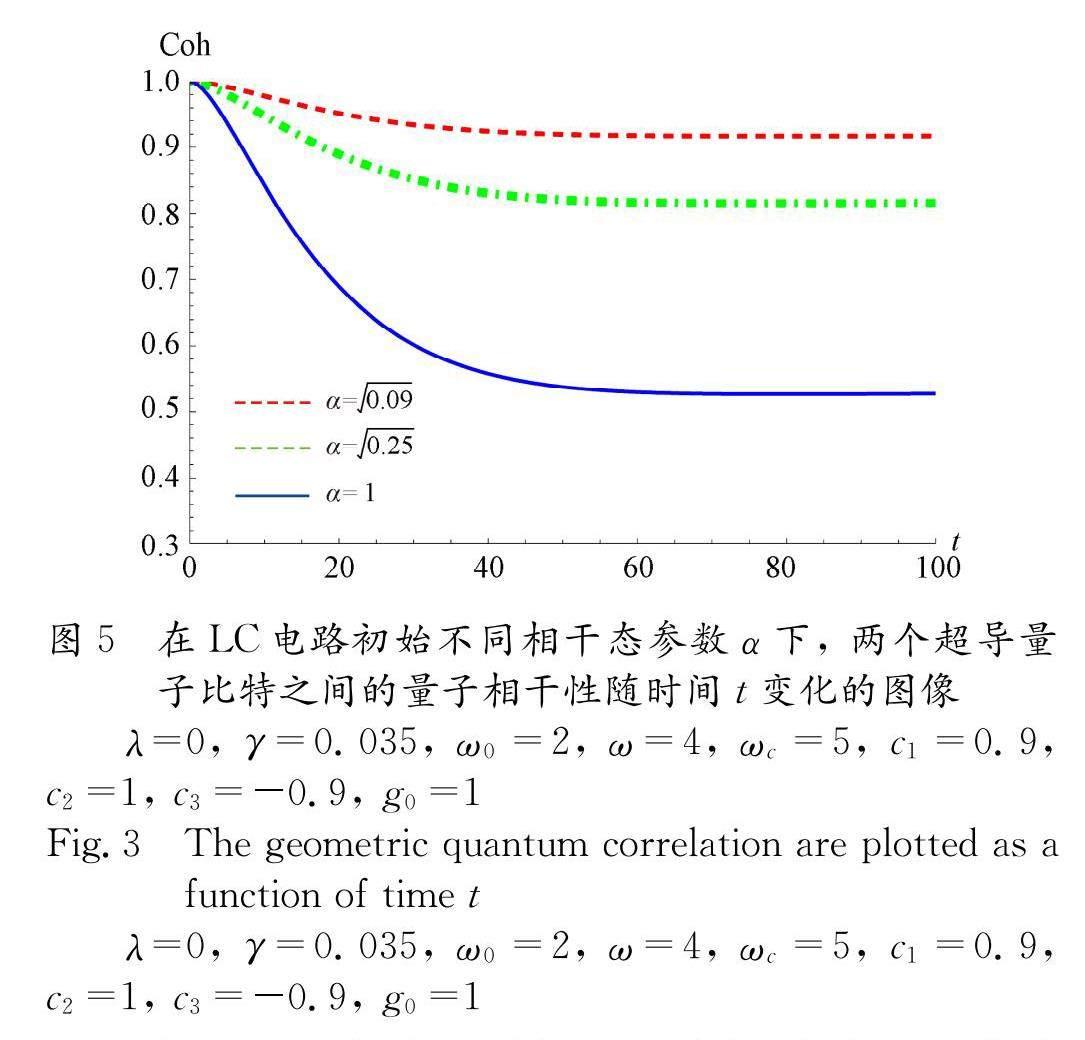
圖5展示了未加入含時電磁場時兩超導量子比特間量子相干性對 LC 電路初始相干態參數 α 的敏感程度. 從圖中可以看出， 兩超導量子比特間的量子相干性不會被完全摧毀， 會在經過衰減之后穩定在一個數值附近保持不變. 這說明開放超導量子電路系統中的量子相干性會被部分保留并出現穩態量子相干性， 并且這個穩態數值會隨著 LC 電路初始相干態參數 α 的增大而減小. 這一現象發生的物理原因是隨著初始相干態參數 α 的增大， 超導量子比特與 LC 電路， 以及 LC 電路與環境之間發生了更加頻繁的相互作用， 所以初始兩超導量子比特間的量子相干性更快地泄露到環境中， 從而導致穩態量子相干性減小.

為了展示含時電磁場對開放超導量子電路系統中超導量子比特間量子相干性的影響， 圖6刻畫了在不同強度的含時電磁場下， 量子相干性隨時間 t 的變化圖像. 從圖中可以發現， 當加入含時電磁場后， 超導量子比特間量子相干性衰減的速率減小; 且提高含時電磁場的強度， 穩態量子相干性的數值得到有效增加. 這些結果都說明， 開放超導量子電路系統中兩超導量子比特間的穩態量子相干性可以通過含時電磁場來進行調節， 即可以通過含時電磁場來提高穩態量子相干性的數值， 并且含時電磁場強度越大， 效果越好.

4 ?含時電磁場對開放超導量子電路系統量子信息流動的影響

本節利用跡距離的方法研究含時電磁場對開放超導量子電路系統中量子信息流動的影響. 跡距離， 在實驗上可由量子態層析技術獲得 ?［12］ . 當前已有研究表明， 其可以用于探討系統和環境之間的初始關聯對開放系統動力學的影響 ?［36，37］ ， 以及測量系統量子過程的非馬爾可夫性 ?［38-39］ . 相關結果已經被近期實驗證實 ?［40，41］ . 兩個量子態 ρ 1 和 ρ 2 之間的跡距離被定義為 ?［38］

D ρ 1，ρ 2 = 1 2 ?Tr ?ρ 1-ρ 2 ??（17）

這里， ??A = A A ?指的是 A A 正特征值的平方根. 跡距離擁有一些非常重要的性質， 比如 0≤ D ρ 1，ρ 2 ?≤1 ， 其中 D ρ 1，ρ 2 =0 表明 ρ 1=ρ 2 ， ??D ρ 1，ρ 2 ?=1 表明 ρ 1 與 ρ 2 正交. 另外， 對于正定的保跡量子操作 ?Λ ?， ?D ?Λ ρ 1， Λ ρ 2 ≤D ρ 1，ρ 2 ?. 而且跡距離在幺正變換下保持不變， 即 ?D Uρ 1U ，Uρ 2U ? =D ρ 1，ρ 2 ?. 以上性質都為利用跡距離來度量系統與環境之間信息交換提供了有效保障. 結合（9）式、（10）式和（17）式， 我們可以得到開放超導量子電路系統的跡距離表達式 ?D（ρ ?ab （0） ，ρ ?ab （t）） .

圖7展示了未加入含時電磁場時兩超導量子比特間跡距離 D（ρ ?ab （0），ρ ?ab （t）） 在不同 LC 電路初始相干態參數 α 下的變化情況. 從圖中可以看出， 隨著 LC 電路初始相干態參數 α 的增大， 跡距離的增加幅度和速率都變大. 這說明隨著初始相干態參數 α 的增大， 超導量子比特與 LC 電路， 以及 LC 電路與環境之間的信息流動變得更頻繁， 從而導致超導電路系統初始所擁有的額量子信息更快地泄露到環境中， 從而丟失原本所具有的量子性質.

為了說明含時電磁場對開放超導量子電路系統中量子信息流動的影響， 圖8展示了在不同強度的含時電磁場下， 跡距離 D（ρ ?ab （0），ρ ?ab （t）） 隨時間 t 的變化圖像. 對比圖中的實線、虛線和點虛線可以明顯看出， 含時電磁場可以減緩跡距離增加的速率和幅度， ?有效抑制超導量子電路系統與環境之間的信息流動. 同時， 隨著含時電磁場強度的增強， 跡距離增加的速率和幅度進一步降低. 這些結果都表明， 含時電磁場可以有效阻礙超導量子電路系統與環境之間的信息交換， 抑制它們之間的信息流動， 從而降低超導量子電路系統初始擁有的量子性質被破壞的程度.

5 結 論

本文研究了利用含時電磁場延長開放超導量子電路系統中幾何量子關聯突然轉變時間的可能性. 研究結果表明， 開放超導量子電路系統中兩超導量子比特間的幾何量子關聯初始時保持不變， 當超過轉變時刻 t 1 后開始衰減. 這說明開放超導量子電路系統中發生了從經典退相干到量子退相干的突然轉變現象， 且轉變時間的長短隨 LC 電路初始相干態參數 α 的增加而減小. 另外， 當加入含時電磁場后， 系統中突然轉變的時間也就是幾何量子關聯保持常量的時間延長. 并且隨著含時電磁場強度的提高， 幾何量子關聯保持常量的時間得到更有效的增加.

本文還研究了含時電磁場對于開放超導量子電路系統量子相干性的影響. 從結果可以發現， 兩超導量子比特間的量子相干性不會被完全摧毀， 也就是說兩超導量子比特間形成穩態量子相干性. 含時電磁場的加入， 使超導量子比特間量子相干性衰減的速率減小. 而且含時電磁場強度越大， 穩態量子相干性被提升的效果越好.

最后借助跡距離的方法探討了含時電磁場對于開放超導量子電路系統與環境之間量子信息流動的影響. 結果顯示， 在未加入含時電磁場時， 兩超導量子比特間跡距離上升的幅度和速率都隨相干態參數 α 的增大而增加. 但是值得注意的是， 通過加入含時電磁場， 兩超導量子比特間跡距離上升的幅度和速率都減緩. 而且， 隨著含時電磁場強度的增加， 跡距離上升的速率和幅度變得更小. 這些結果表明， 含時電磁場可以有效阻礙超導量子電路系統與環境之間的信息交換， 抑制它們之間的信息流動， 保護超導量子電路系統初始擁有的量子性質.

參考文獻：

［1］ ??Makhlin Y， Schon G， Shnirman， A. Quantum-state engineering with Josephson-junction devices ［J］. Rev Mod Phys， 2001， 73： 357.

［2］ ?Johansson J， Saito S， Meno T， ?et al. ?Vacuum Rabi oscillations in a macroscopic superconducting qubit LC oscillator system ［J］. Phys Rev Lett， 2006， 96： 127006.

［3］ ?Liu Y X， Sun C P， Nori F. Scalable superconducting qubit circuits using dressed states ［J］. Phys Rev A， 2006， 74： 052321.

［4］ ?Wang D M， Xu H S， Xu J B， ?et al. ?Enhancement of geometric discord for the system of superconducting qubits and transfer of quantum information ［J］. J Opt Soc Am B， 2013， 30： 2277.

［5］ ?Kang Y H， Chen Y H， Wu Q C， ?et al. ?Fast generation of W states of superconducting qubits with multiple Schrodinger dynamics ［J］. Sci Rep， 2016， 6： 36737.

［6］ ?Hime T， Reichardt P A， Plourde B L T， ?et al. ?Solidstate qubits with current-controlled coupling ［J］. Science， 2006， 314： 1427.

［7］ ?Kielpinski D， Kafri D， Woolley M J， ?et al. ?Quantum interface between an electrical circuit and a single atom ［J］. Phys Rev Lett， 2012， 108： 130504.

［8］ ?Motte D D， Grounds A R， Rehák M， ?et al. ?Experimental system design for the integration of trapped-ion and superconducting qubit systems ［J］. Quantum Inf Process， 2016， 15： 5385.

［9］ ?Chiorescu I， Bertet P， Semba K， ?et al. ?Coherent dynamics of a flux qubit coupled to a harmonic oscillator ［J］. Nature， 2004， 431： 159.

［10］ ?Ladd T D， Jelezko F， Laflamme R， ?et al. ?Quantum computers ［J］. Nature， 2010， 464： 45.

［11］ Kurizki G， Bertet P， Kubo Y， ?et al. ?Quantum technologies with hybrid systems ［J］. Proc Nat Acad Sci， 2015， 112： 3866.

［12］ Nielsen M A， Chuang I L. Quantum computation and quantum information ［M］. London： Cambridge University Press， 2000： 880.

［13］ Meyer D A. Sophisticated quantum search without entanglement ［J］. Phys Rev Lett， 2000， 85： 2014.

［14］ Zhang Y J， Han W， Xia Y J， ?et al. ?Role of initial system-bath correlation on coherence trapping ［J］. Sci Rep， 2015， 5： 13359.

［15］ Liu X B， Tian Z H， Wang J C， ?et al. ?Protecting quantum coherence of two-level atoms from vacuum fluctuations of electromagnetic field ［J］. Ann Phys， 2016， 366： 102.

［16］ Wu W， Cheng J Q. Coherent dynamics of a qubitCoscillator system in a noisy environment ［J］. Quantum Inf Process， 2018， 17： 300.

［17］ Huang Z M， Situ H Z. Non-Markovian dynamics of quantum coherence of two-level system driven by classical field ［J］. Quantum Inf Process， 2007， 16： 222.

［18］ Guarnieri G， Kolá r ??ˇ ???M， Filip R. Steady-state coherences by composite system-bath interactions ［J］. Phys Rev Lett， 2018， 121： 070401.

［19］ Mukhopadhyay C. Generating steady quantum coherence and magic through an autonomous thermodynamic machine by utilizing a spin bath ［J］. Phys Rev A， 98： 012102.

［20］ Hu M L， Zhou W. Enhancing two-qubit quantum coherence in a correlated dephasing channel ［J］. Laser Phys Lett， 2019， 16： 045201.

［21］ Borivoje ?D， Vlatko V， Caslav B. Necessary and sufficient condition for nonzero quantum discord ［J］. Phys Rev Lett， 2010， 105： 190502.

［22］ Paula F M， Montealegre J D， Saguia A， ?et al . Geometric classical and total correlations via trace distance ［J］. Europhys Lett， 2013， 103： 50008.

［23］ Paula F M， Silva I A， Montealegre J D， ?et al . Observation of nvironment-induced double sudden transitions in geometric quantum correlations ［J］. Phys Rev Lett， 2013， 111： 250401.

［24］ Lostaglio M， Korzekwa K， Milne A. Markovian evolution of quantum coherence under symmetric dynamics ［J］. Phys Rev A， 2017， 96： 032109.

［25］ Wu W， Xu J B. Quantum coherence of spin-boson model at finite temperature ［J］. Ann Phys， 2017， 48： 377.

［26］ Yin S Y， Song J， Xu X X， ?et al. ?Quantum coherence dynamics of threequbit states in XY spin-chain environment ［J］. Quantum Inf ?Process， 2018， 17： 296.

［27］ Yadin B， Bogaert P， Susa C E， ?et al. ?Coherence and quantum correlations measure sensitivity to dephasing channels ［J］. Phys Rev A， 2019， 99： 012329.

［28］ Liu Y X， Wei L F， Johansson J R， ?et al. ?Superconducting qubits can be coupled and addressed as trapped ions ［J］. Phys Rev B， 2007， 76： 144518.

［29］ Nigg ?S E， Fuhrer A， Loss D. Superconducting grid-bus surface code architecture for hole-spin qubits ［J］. Phys Rev Lett， 2017， 118： 147701.

［30］ Khan S， Tureci H E. Frequency combs in a lumped-element josephson-junction circuit ［J］. Phys Rev Lett， 2018， 120： 153601.

［31］ van den Brink A M. Hamiltonian for coupled flux qubits ［J］. Phys Rev B， 2005， 71： 064503.

［32］ Zheng S B， Guo G C. Efficient scheme for two-atom entanglement and quantum information processing in cavity QED ［J］. Phys Rev Lett， 2000， 85： 2392.

［33］ Peixoto de Faria J G， Nemes M C. Dissipative dynamics of the Jaynes-Cummings model in the dispersive approximation： analytical results ［J］. Phys Rev A， 1999， 59： ?3918.

［34］ Xu J B， Zou X B. Dynamic algebraic approach to the system of a three-level atom in the Λ configuration ［J］. Phys Rev A， 1999， 60： 4743.

［35］ Dukalski M， Blanter Y M. Periodic revival of entanglement of two strongly driven qubits in a dissipative cavity ［J］. Phys Rev A， 2010， 82： 052330.

［36］ Laine E M， Piilo J， Breuer H．Witness for initial system-environment correlations in open-system dynamics ［J］. Eur Phys Lett， 2010， 92： 60010．

［37］ Smirne A， Breuer H P， Piilo J， ?et al. ?Initial correlations in open-systems dynamics： the Jaynes-Cummings model ［J］. Phys Rev A， 2010， 82： 062114.

［38］ Breuer H P， Laine E M， Piilo J. Measure for the degree of non-markovian behavior of quantum processes in open systems ［J］. Phys Rev Lett， 2009， 103： 210401.

［39］ Laine E M， Piilo J， Breuer H P. Measure for the non-Markovianity of quantum processes ［J］. Phys Rev A， 2010， 81： 062115.

［40］ Liu B H， Li L， Huang Y F， ?et al. ?Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems ［J］. Nature Phys， 2011， 7： 931.

［41］ Tang J S， Li C F， Li Y， ?et al. ?Measuring non-Markovianity of processes with controllable system-environment interaction ［J］. Europhys Lett， 2012， 97： 10002.

收稿日期： ?2023-05-24

基金項目： ??國家自然科學基金（11364006，11264008）； 貴州省科技計劃項目（黔科合LH字［2017］7343）； 貴州省普通高等學校低維凝聚態物理重點實驗室項目（黔教合KY字［2016］002）； 貴州師范大學博士基金

作者簡介： ??吳春艷（1997-）， 女， 貴州盤縣人， 碩士研究生， 主要研究領域為量子光學與量子信息.

通迅作者： ?賀啟亮. E-mail： heliang005@163.com