顧及基準點誤差的自由設站平差及精度分析

劉瓊瓊，閆廣峰

（1. 周口市規劃建筑勘測設計院，河南 周口 466000；2. 內江師范學院地理與資源科學學院，四川 內江 641100）

自由設站法是目前測量實踐中，利用全站儀進行地形圖測量、施工放樣、變形監測等測量工作的常用方法，其具有設站位置選擇靈活、工效高、精度高、控制點間不要求通視等優點。國內外學者圍繞自由設站方法開展了大量的基礎理論和應用研究[1-5]。目前進行自由設站的數據處理時，通常采用經典約束平差法，其以所有聯測的基準點為固定點、所有水平方向和水平距離測量值為觀測值，并以設站點坐標和定向角為待求參數進行求解。然而，由于測量誤差、平差模型等因素的影響，自由設站采用的基準點坐標會含有誤差，測站約束平差后其會以原始數據誤差[6]的形式影響設站點坐標和定向角估值，進而影響碎部點坐標。特別當基準點精度較低時，這種不利的影響將更為顯著。為此，本文在分析自由設站基本原理基礎上，基于部分變量誤差（partial errors-in-variables，Partial EIV） 模型平差理論和方法，以新的思路解決自由設站平差問題。

1 全站儀自由設站基本原理

全站儀自由設站外業觀測如圖1 所示，其中，P為設站點，A～E為基準點（不少于2個），P1和P2為待測量碎部點。

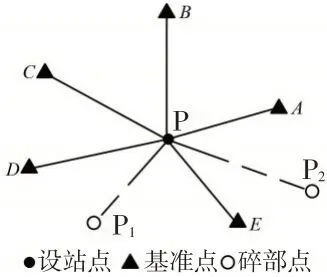
圖1 全站儀自由設站外業觀測示意圖

目前進行自由設站測量數據處理時，將P 點坐標XP、YP和測站的定向角φ作為待求參數，P 點觀測A～E 點的水平方向測量值LA～LE、距離測量值SA～SE為觀測值，A～E點坐標XA、YA...XE、YE為固定值，由此建立自由設站平差問題的數學模型。

1）函數模型：

2）隨機模型：

式中，ΔφP為定向角改正數；為點P 的近似坐標改正數；為點P 和點i 的近似坐標較差；ρ″=206265 為常數；LPi和分別為Pi 的方向觀測值和近似方向值；SPi和分別為Pi的距離觀測值和近似距離值；D為觀測值的協方差陣；σ0為先驗單位權中誤差；Q為觀測值協因數陣；P為觀測值的權陣，可按照經驗定權法并結合儀器標稱精度確定。

根據最小二乘原理，由式（1）求解參數XP、YP、φ的估值?，再由P 點觀測碎部點P1、P2的水平方向和水平距離觀測值L1、L2、S1、S2，根據極坐標原理可得到P1、P2點的坐標：

式中，Xi、Yi為第i個碎部點坐標，i=1,2。

由原始數據誤差理論[6]可知，以上基于經典約束平差方法進行自由設站數據處理，平差前后的基準點坐標不變，基準點誤差會以原始數據誤差的形式影響設站點坐標、測站定向角估值，并進一步傳遞至碎部點坐標。當設站采用的基準點精度較低時，原始數據誤差給自由設站精度帶來的不利影響不容忽視。

為解決經典約束平差模型難以顧及自由設站基準點誤差的問題，本文探索以新的思路解決自由設站數據處理問題。注意到圖1中，若以P為坐標系原點，P觀測基準點A的方向PA為x軸，x軸順時針旋轉90°方向為y 軸，建立平面直角坐標系，則根據P 點觀測的水平方向、水平距離觀測值可求得基準點、碎部點在該站心坐標系的平面坐標。由基準點在站心坐標系、測量坐標系下的2 套坐標，可建立基準點兩套坐標間的坐標轉換平差模型，若建立的模型能夠準確表達2個坐標系之間的相對空間位置關系，便可根據求得的模型轉換參數求解得到設站點和碎部點在測量坐標系的坐標。

2 顧及基準點誤差的自由設站平差模型

以設站點P 為坐標系原點，P 點至聯測的任一基準點方向為X軸，X軸順時針旋轉90°方向為Y軸，建立站心坐標系。根據P至各基準點和碎部點的水平方向、水平距離觀測值，可求得基準點、碎部點的站心坐標系坐標。要進一步得到設站點和碎部點的測量坐標系下坐標，必須找到站心坐標系和測量坐標系間的相對空間位置關系。為此，基于基準點在站心坐標和測量坐標系下的2 套坐標，建立2 個坐標系間的坐標轉換模型。

由于基準點的建網測量與自由設站測量時可能采用不同的技術手段，因此，2 個坐標系之間可能會存在一定的尺度差異。為此，建立能夠完整表達站心坐標系與測量坐標系之間存在的平移、旋轉和尺度差異關系的相似變換坐標轉換模型[7-8]：

式中，和分別為第i個基準點的測量坐標系坐標和站心坐標系坐標，i=1,2,...,n；X0、Y0為平移參數；m為尺度因子；α為旋轉角。

令Z1=mcosα、Z2=msinα，并設

則式（4）可表示為線性模型：

式（5）的系數矩陣A由常數0、1以及基準點的站心坐標構成。進一步考慮式（5）中的基準點站心坐標誤差，可得坐標轉換Partial EIV模型

式中，為系數矩陣A的真值矩陣；el為l 對應的隨機誤差向量；EA為A對應的改正數矩陣，其固定值對應部分為0，相同隨機元素對應的改正數相同。

將式（6）看作非線性Gauss-Helmert 模型[9]，并將EA中隨機量作為待求參數，則式（6）可表示為：

式中，為a的真值向量；EA為系數矩陣A對應的改正數矩陣；觀測值為 ；待求參數為。

采用高斯-牛頓法迭代方法對式（7）求解[9]。設第i 次迭代后，參數X的估值為X(i)，eAs的估值為eAs(i)，將式（7）右端在()X(i)，eAs(i)處用泰勒級數展開并取至一階項

式中，δX為X(i)的微小改正值；R為與X(i)、EA的有關的矩陣，滿足ReAs=EAX(i)。

以式（9）為目標函數：

對各變量求偏導且令導數等于0，可得：

以參數的最小二乘解為初值，根據式（10）、式（11）進行迭代計算，直至<ε （ε 為小的常數）時迭代結束。由此得到測量坐標系和站心坐標系之間的坐標轉換參數估值和。

進一步計算尺度因子m、旋轉角α的平差值：

式中，arctan(x)為對x求反正切。

則設站點、碎部點在測量坐標系下的坐標為：

從以上自由設站數據處理過程可以看出，相較于經典的約束平差法，所建立的平差模型，給系數矩陣引入誤差向量，考慮了觀測誤差對自由設站平差的影響；以基準點的測量坐標系坐標為觀測值，能夠顧及到基準點誤差的影響。為敘述方便，稱以上方法為顧及基準點誤差的自由設站平差法（free stationing adjustment considering the datum point errors， 簡稱FSA-CDPE）。

3 實驗設計與結果分析

為了評估FSA-CDPE方法進行自由設站數據處理的可行性和有效性，基于某建筑工程的放樣測量實際，設計全站儀自由設站仿真實驗。外業觀測如圖2所示，采用自由設站方法進行碎部點放樣，其中，A～D為基準點，P 為設站點，P1和P2為待測量碎部點。

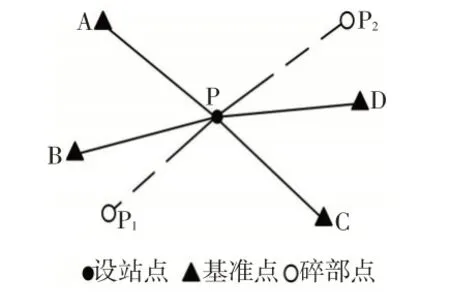
圖2 全站儀自由設站法測量

設站點P 至各基準點、碎部點的方位角和距離為方向、距離觀測值模擬真值，分別如表1、2所示。

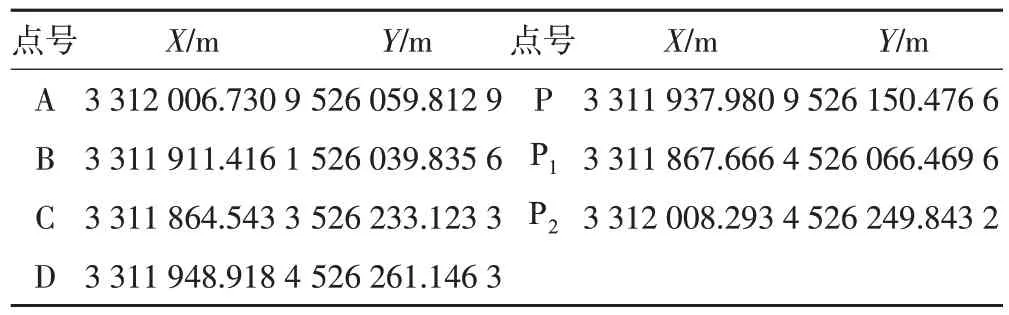
表1 各點測量坐標系的坐標真值

表2 觀測值模擬真值

利用隨機數發生器，首先給P 至各基準點、碎部點的觀測值添加觀測誤差，其中，添加的方向觀測值中誤差為±1.0″ ，距離觀測值固定誤差為±1.0 mm、比例誤差為±1.5 ppm，各基準點、碎部點均觀測2 個測回。再往基準點A～D的X、Y的坐標中分別添加5種不同中誤差σ大小的正態分布隨機誤差，具體方案為：①u=0、σ=1.0 mm；②u=0、σ=2.0 mm；③u=0、σ=3.0mm；④u=0、σ=4.0mm；⑤u=0、σ=5.0mm。

分別采用經典約束平差法、FSA-CDPE 法進行自由設站平差，并用平差后的設站點和碎部點坐標真誤差平方和M評定平差結果的整體準確度（M 越小，自由設站平差結果準確度越高），用點位真誤差TP衡量設站點和碎部點的平差結果準確度。

設碎部點和設站點個數共計為k，M可采用下式求解：

式中，為碎部點或設站點的平差值；、為碎部點或設站點的真值。

TP的計算公式為：

5種方案的實驗結果如表3所示。

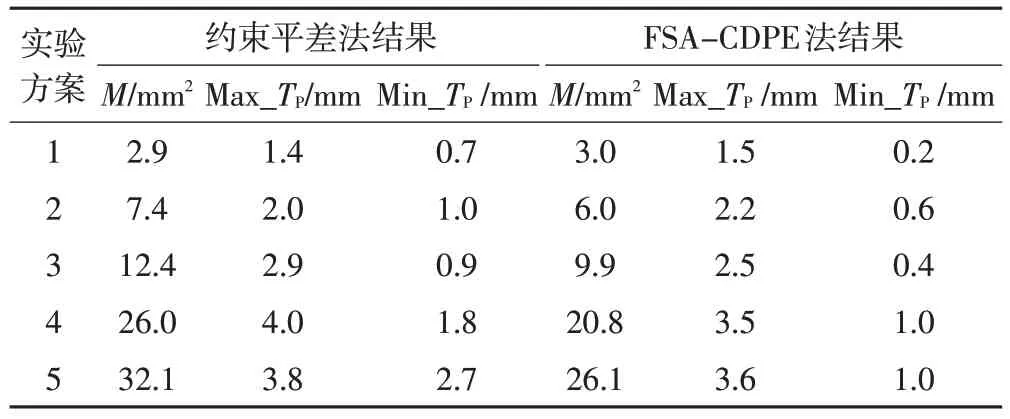
表3 各實驗方案結果

表3 中，Max_TP、Min_TP分別為平差后設站點、碎部點的點位真誤差最大值和最小值。從表3 的實驗結果可以看出，無論是采用約束平差法還是FSA-CDPE 法，隨著給基準點坐標添加誤差值的變大，坐標真誤差平方和M逐漸變大，設站點和碎部點的點位真誤差也呈增大趨勢。此外，還可以發現，當給基準點添加的誤差較小時，采用約束平差方法和FSA-CDPE 方法的自由設站平差結果相當，如方案1、2 中，2 種方法的坐標真誤差平方和M 和點位真誤差均相差較小；隨著往基準點中添加誤差量級變大，2 種方法的平差效果差異明顯，如方案5 中，約束平差結果的坐標真誤差平差和M為32.1、最大和最小點位真誤差為3.8 和2.7，而FSA-CDPE 方法的M 值為26.1、點位真誤差最大值3.6、最小值1.0。

通過以上分析可以得出，較大的基準點誤差會給自由設站平差結果的精確度帶來不利影響；FSA-CDPE 方法用于自由設站數據處理是可行且有效的，當基準點精度較高時，其與經典約束平差方法結果相當；但當基準點精度較低時，其平差結果較約束平差方法更優。

4 結語

通過初步的理論和實驗分析，可以得到以下結論：

1）進行自由設站數據處理時，應兼顧基準點誤差的影響。否則當基準點誤差較大時，其會給平差結果帶來較大的不利影響。

2）FSA-CDPE方法與經典約束平差法進行自由設站數據處理，當基準點的精度較高時，2 種方法的結果相當；基準點精度較低時，前種方法較后種方法得到的結果更優。

3）FSA-CDPE方法用于自由設站數據處理是可行且有效的，其平差模型同時考慮了全站儀測量誤差和基準點誤差的影響，理論上是嚴密的，為全站儀自由設站數據處理提供了一種新的思路和有效方法。