剪拼構造法的實踐探究

朱海燕

(浙江省寧海縣城關中學,浙江 寧波 315600)

三角形是初中幾何中最基本的圖形,全等三角形的判定與性質是解決幾何問題的重要工具.本文以具體的幾何問題為例,說明剪拼構造法在解題中的應用,以此培養學生的幾何推理能力.

1 題目呈現

如圖1,在△ABC中,AD是BC邊上的中線,F是AD上一點,延長BF交AC于點E,AE=EF,求證：BF=AC.

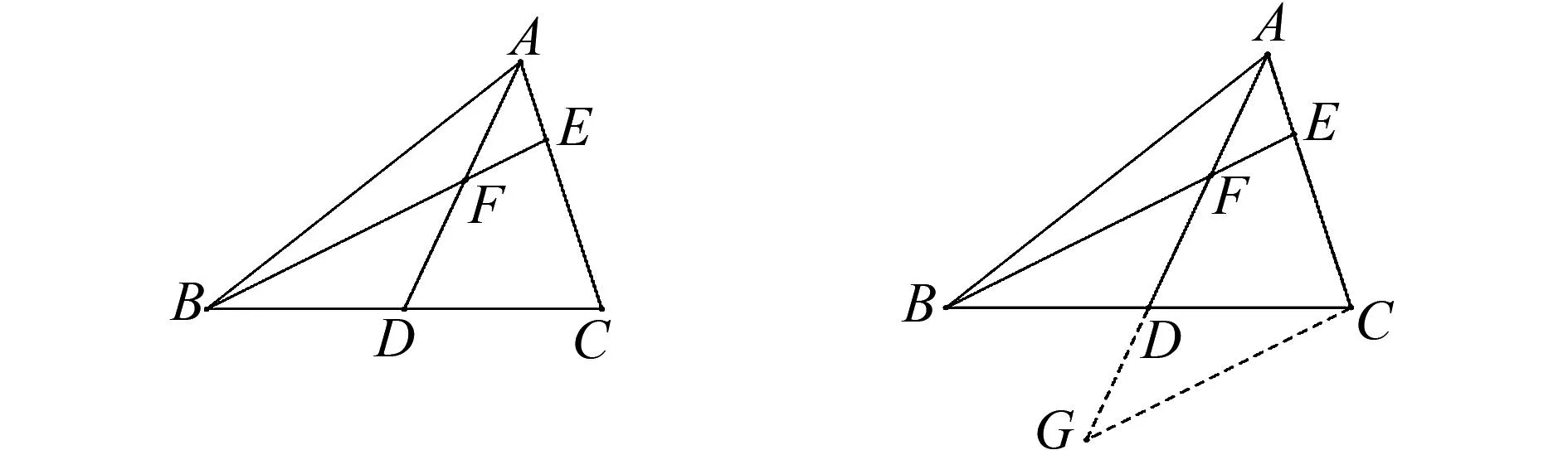
圖1 △ABC示意圖 圖2 倍長中線示意圖

學生根據已有的經驗會想到倍長中線,如圖2和圖3所示.倍長中線法的本質是構造全等三角形,再結合生成的等腰三角形,通過等量代換證明結論.

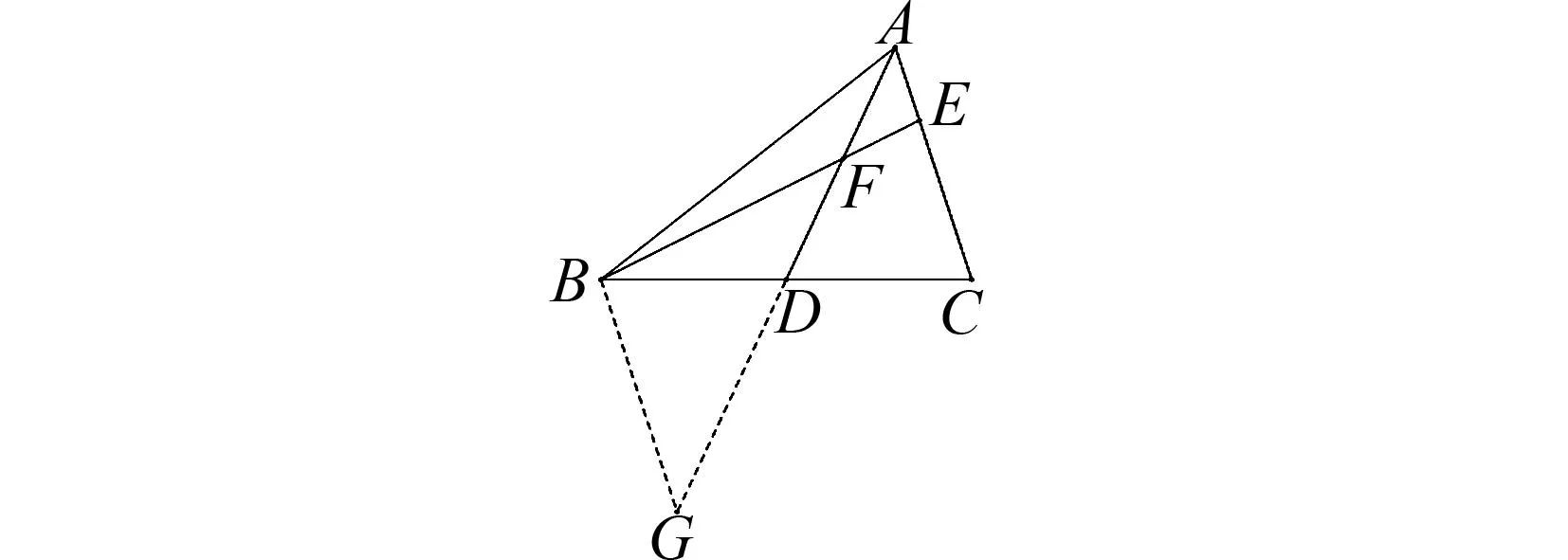
圖3 倍長中線示意圖

2 嘗試剪拼構造

通過學習,學生已經掌握了全等三角形的定義,即能夠完全重合的兩個三角形叫作全等三角形.若將圖2中的△BDF剪下來,會與△CDG重合.利用逆向思考方法,可以將圖2看成是將△BDF剪拼至△CDG后生成的構造圖.類似地,圖3可以看成是將△ACD剪拼至△GBD構造得到.由此可以看出,可以嘗試利用剪拼法構造全等三角形[1].

下面嘗試對△BDF進行剪拼.剪雖易,拼卻不易,拼到哪里去?怎么拼?再次觀察圖2,發現可以看成是以BD=CD為條件進行剪拼的.

2.1 以BD=DC為條件進行剪拼

如圖4,將△BDF剪拼至△DCG,易發現CG∥AD,△AOD與△COG都是等腰三角形.故添加輔助線后可進行如下推理：過點C作CG∥AD,且CG=DF,連接DG.易得△BDF≌△DCG,所以∠BFD=∠G.因為AE=EF,CG∥AD,所以∠DAO=∠ADO=∠G=∠ACG,所以△AOD與△COG都是等腰三角形,所以OG=OC,OA=OD,所以AC=DG=BF.

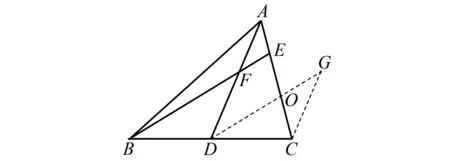
圖4 △BDF剪拼至△DCG示意圖

如圖5,將△BDF剪拼至△CDG,此法即為圖2中的倍長中線構造法.

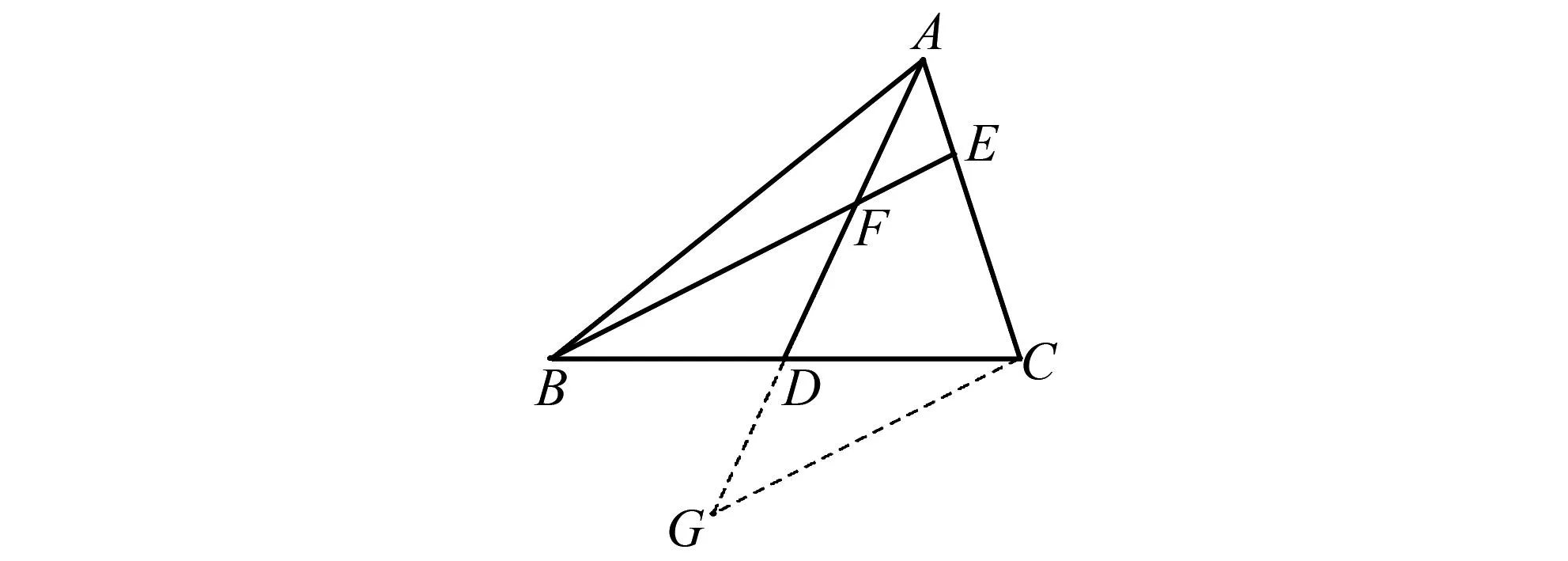
圖5 △BDF剪拼至△CDG示意圖

2.2 以DF=DF為條件進行剪拼

如圖6,將△BDF剪拼至△GDF,生成了等腰三角形BFG和平行四邊形AFGC.由此可進行如下推理：過點F作∠DFG=∠BFD,且使FG=BF,則△BFG為等腰三角形.由等腰三角形性質可得BH=GH.又因為BD=CD,所以DH是△BGC的中位線,所以DH∥GC.又易證AC∥FG,所以四邊形ACGF是平行四邊形,所以AC=FG=FB.

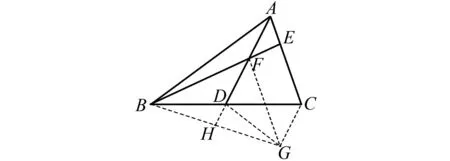
圖6 △BDF剪拼至△GDF示意圖

如圖7,將△BDF剪拼至△GFD,生成平行四邊形BDGF、等腰△AOD及等腰△COG,圖形結構與圖4相同,證法類似,不再贅述.

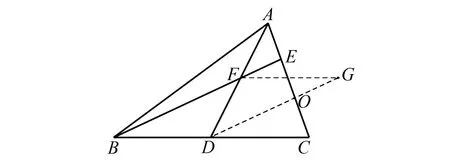
圖7 △BDF剪拼至△GFD示意圖

2.3 以BF=AC為條件進行剪拼

如圖8,將△BDF剪拼至△CGA,生成等腰△DCG.故添加適當的輔助線后可得如下推理：過點C作CG=CD,交AD于點G,則∠FDC=∠DGC.又因為∠FAE=∠BFD,所以∠ACG=∠FBD.因為BD=CD,CD=CG,所以CG=BD,故可證△BDF≌△CGA,所以BF=AC.

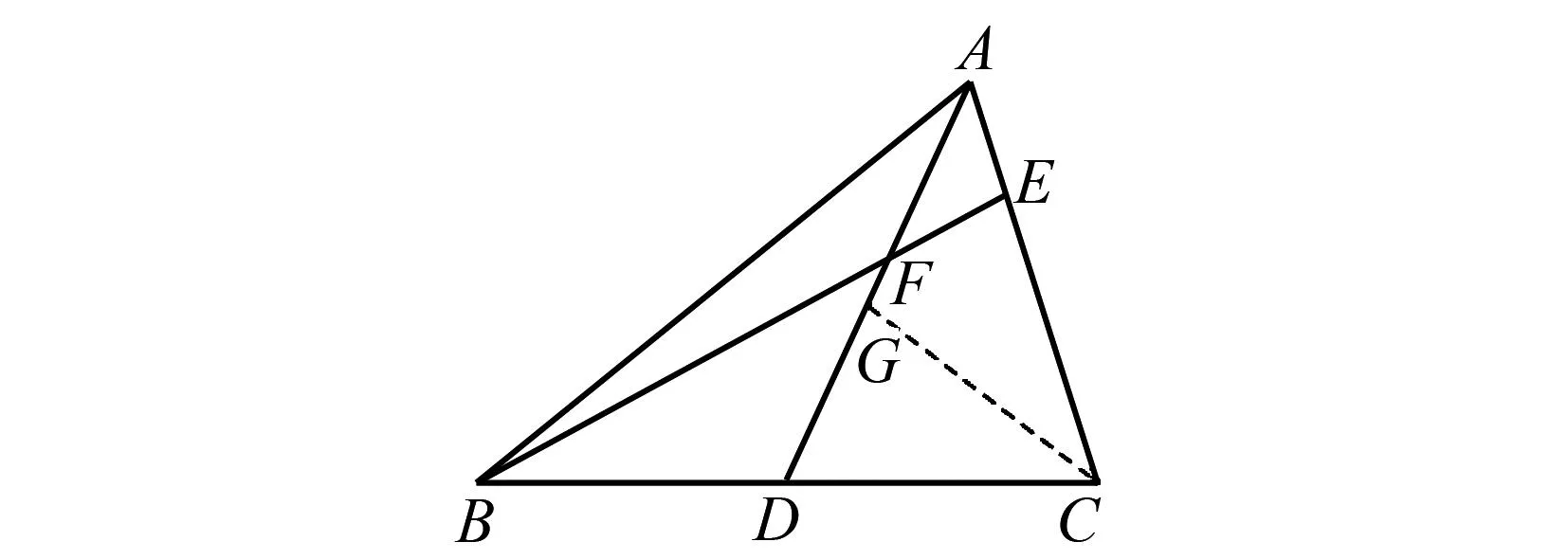
圖8 △BDF剪拼至△CGA示意圖

如圖9,將△BDF剪拼至△AGC,生成等腰梯形ADCG.證明過程從略,請讀者自行探究.

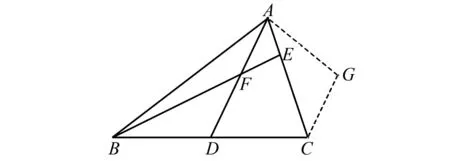
圖9 △BDF剪拼至△AGC示意圖

如圖10,將△BDF剪拼至△CGA,生成A、D、C、G四點共圓的結構.推理過程如下：過點C作射線CG使∠ACG=∠FBD.過點A作射線AG使∠CAG=∠DAC,交于點G.通過計算法可證得∠DAG+∠DCG=180°,則點A、D、C、G四點共圓.由∠CAG=∠DAC,可得DC=CG,所以CG=BD.故△CGA≌△BDF,所以AC=BF.

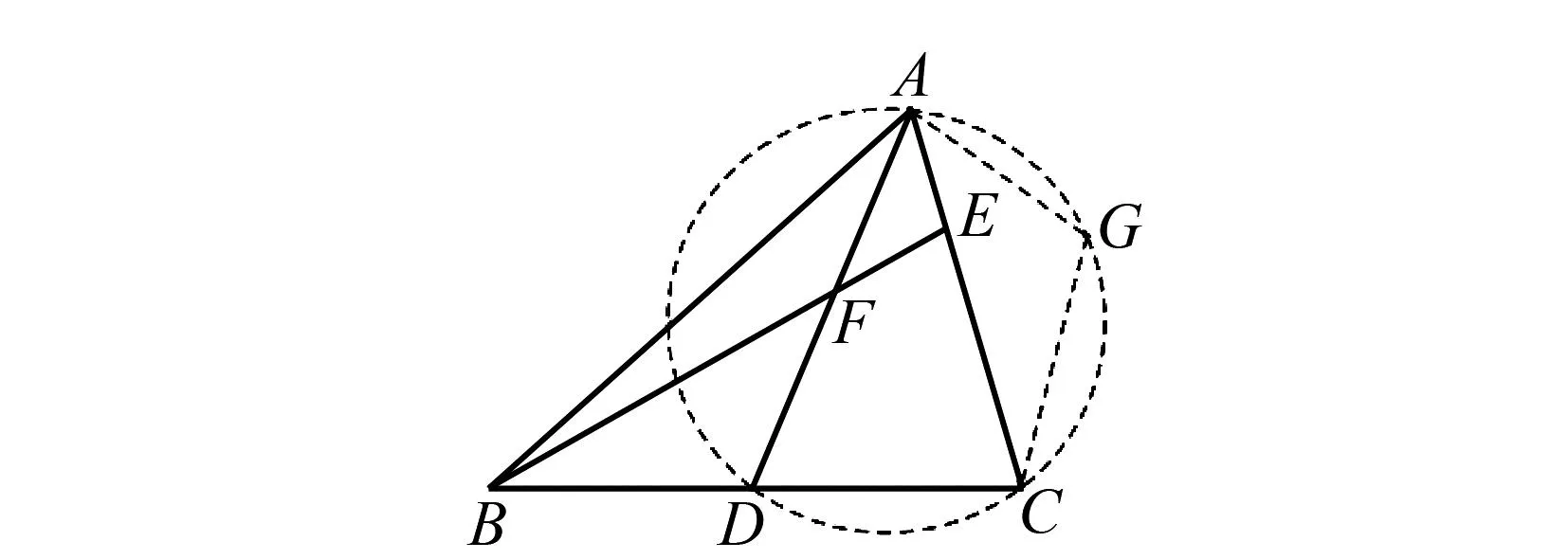
圖10 △BDF剪拼至△CGA示意圖

由此可以看出,剪拼△BDF可以拼出7種圖形,即有7種全等三角形構造法.這種剪拼方法可否應用于剪拼其他三角形?剪拼法能否作為全等三角形構造法的通法呢?為此,需對此法進行驗證.

3 驗證剪拼構造法

3.1 剪拼△ADC,驗證構造法

3.1.1以BF=AC為條件進行剪拼

將剪下來的△ADC的邊AC疊合到BF,可拼出圖11、圖12兩種構圖,其中圖11生成等腰△BDG,圖12生成等腰梯形BDFG.整理思路,添加適當的輔助線,推理驗證易知這種構造法成立.

圖11 等腰△BDG示意圖 圖12 等腰梯形BDFG示意圖

3.1.2以BD=CD為條件進行剪拼

將剪下來的△ADC的邊CD疊合到BD,可拼出圖13～圖15三種構圖,其中圖13生成等腰△BGF,圖14生成兩個等腰三角形,即△BOG和△DOF.圖15生成B、D、F、G四點共圓的特殊結構.整理思路,添加適當的輔助線,推理驗證易知這種構造法成立.

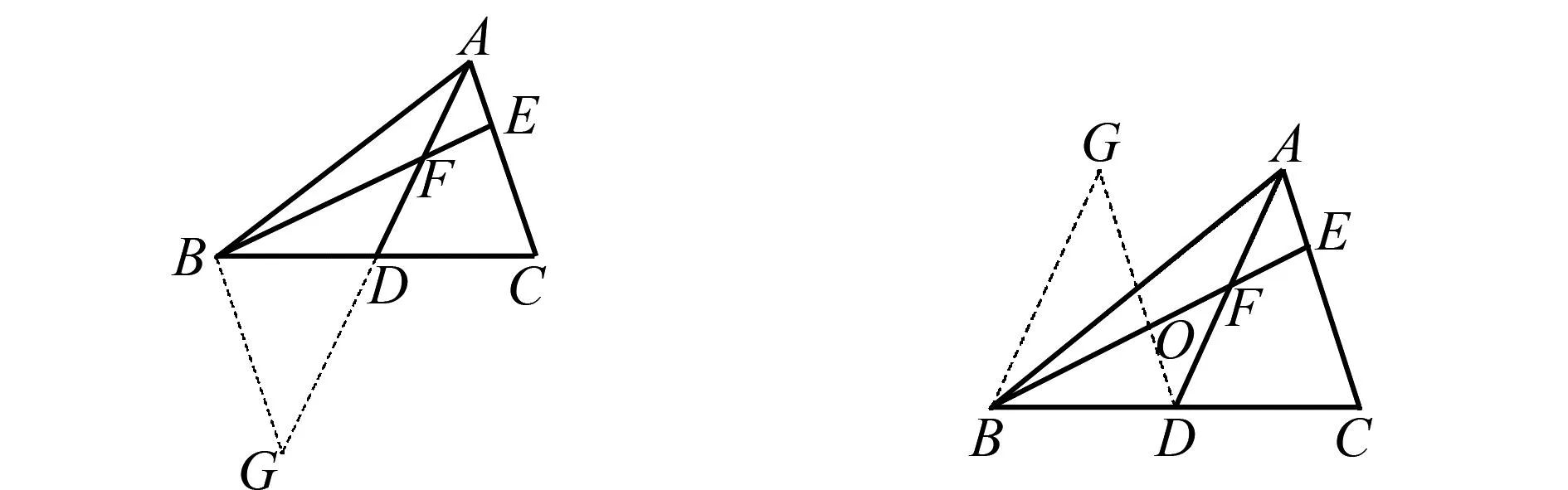
圖13 等腰△BGF示意圖 圖14 等腰△BOG和△DOF示意圖

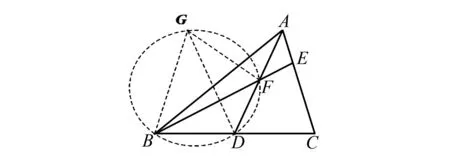
圖15 四點共圓示意圖

3.2 剪拼△ABF,驗證構造法

將剪下來的△ABF的邊AF疊合到AF可拼出圖16,其結構與圖6相同,證法類似,故構法成立.

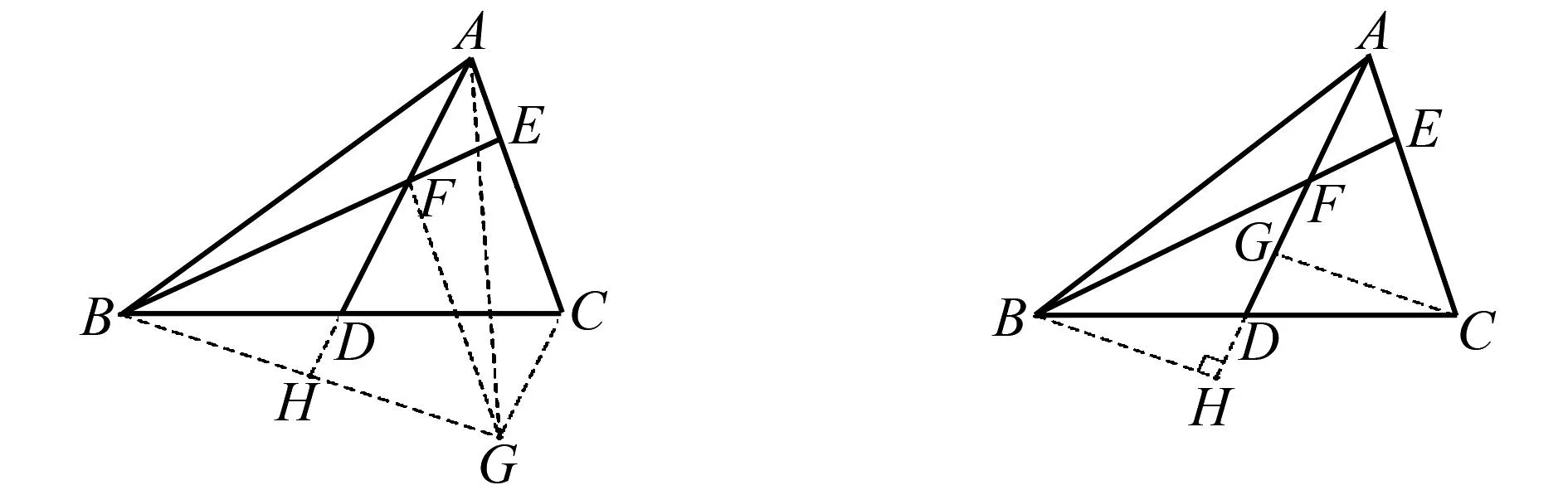
圖16 剪拼△ABF示意圖 圖17 構造直角三角形示意圖

3.3 構造直角三角形,再剪拼

除了剪拼已有三角形外,也可先構造直角三角形再剪拼.過點C作CG⊥AD,構造出Rt△ACG,再將它以AC=BF為條件進行剪拼得圖17.所構圖中,易證△BDH≌△CDG,得BH=CG,于是可證△ACG≌△FBH.故構法成立.

由此可見,剪拼構造法可以作為構造全等三角形的通性通法,它可以為解題助一臂之力.

4 方法歸納

4.1 剪拼構造法的解題步驟

剪拼構造法的解題步驟是：將待證線段或角所在的三角形剪下;在原圖中找出與所剪三角形的邊或角相等的基本元素;以線段的相等或角的相等為基本條件進行疊合拼圖;觀察所拼圖形是否生成特殊結構,以此作為構法成立的基本依據;整理思路,添加適當的輔助線,然后進行推理論證[2].

4.2 剪拼構造法的經驗總結

(1)不同的剪拼可以得到不同的拼圖.通過大量的剪拼試驗,筆者發現有效構圖具備以下幾個特點：①拼圖后生成新的特殊結構,如等腰三角形、等腰梯形、平行四邊形、全等三角形、四點共圓等;②拼圖后能將分散的條件聚攏集中.

(2)剪拼構造法的提煉經歷了“觀察想象——嘗試構造——構法驗證——方法歸納”的探究路徑,這可以成為解題方法探究的基本模式.

5 結束語

總之,在初中數學教學中,教師應該帶領學生進行各種各樣的實踐活動,增加初中數學課堂教學的有效性.實踐性的課堂教學不僅能促進學生對已學知識的深度理解,還能培養學生的探究能力,激發學生的創新思維,提高學生運用所學知識分析問題和解決問題的能力,從而培養其數學核心素養[3].