二次函數(shù)背景下特殊四邊形的存在性問題探究

黃芳

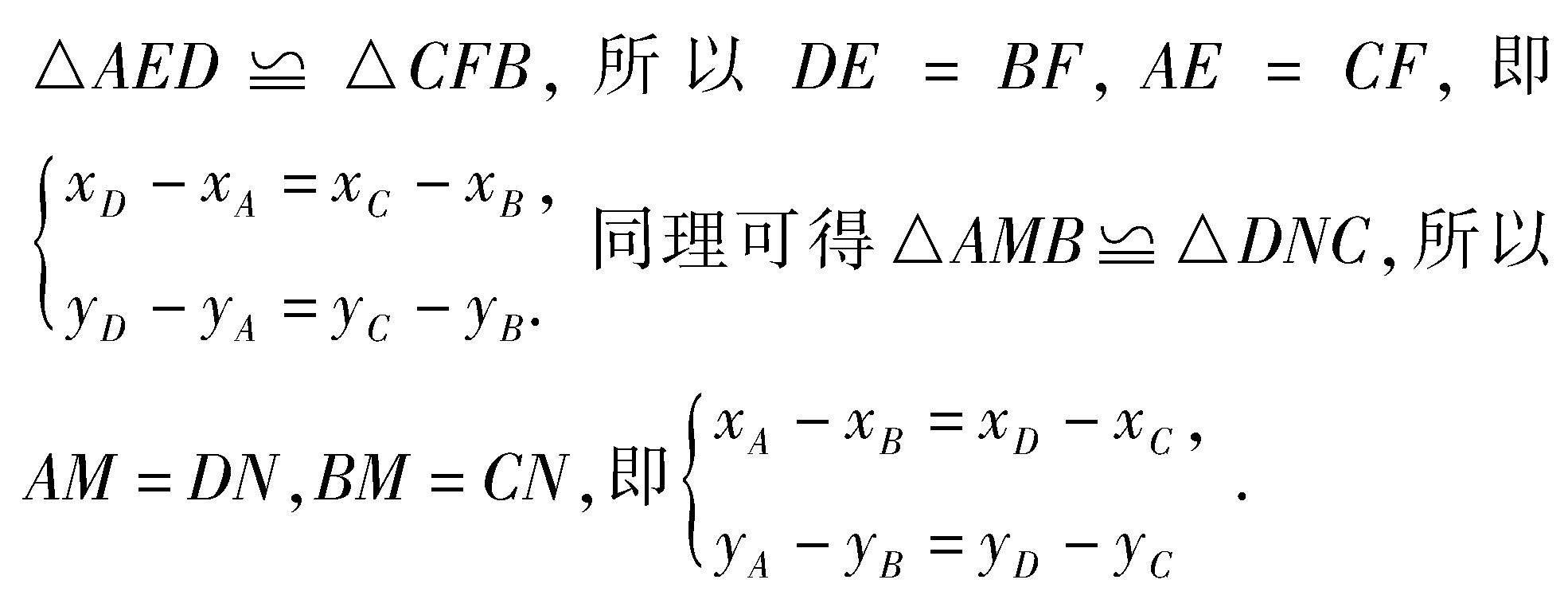
摘 要：二次函數(shù)與四邊形都是初中數(shù)學(xué)的核心內(nèi)容，二次函數(shù)背景下特殊四邊形的存在性問題是中考的重點考查內(nèi)容，常出現(xiàn)在壓軸題中.這類問題難度較大，即使部分優(yōu)秀學(xué)生對此類問題有所掌握，但在解題中也容易出現(xiàn)漏解，特別是用幾何方法時存在作圖準(zhǔn)確性不夠的缺陷.筆者另辟蹊徑，在教學(xué)實踐中將幾何問題代數(shù)化，合理分類，有序組合，利用方程等模型，歸納出解決問題的基本思路和一般方法，取得了較好的效果.

關(guān)鍵詞：二次函數(shù)；特殊四邊形；存在性問題；探究

中圖分類號：G632 文獻標(biāo)識碼：A 文章編號：1008-0333（2024）08-0016-03

在初中階段，平行四邊形、矩形、菱形、正方形等都是特殊的四邊形，其與二次函數(shù)相結(jié)合的中考試題屢見不鮮，這類問題具有一定的選拔功能，對學(xué)生而言具有一定的難度.

1 知識引入

問題1 已知線段AB平行于y軸，A（-2，2），B（-2，-1），線段AB的長度是多少？

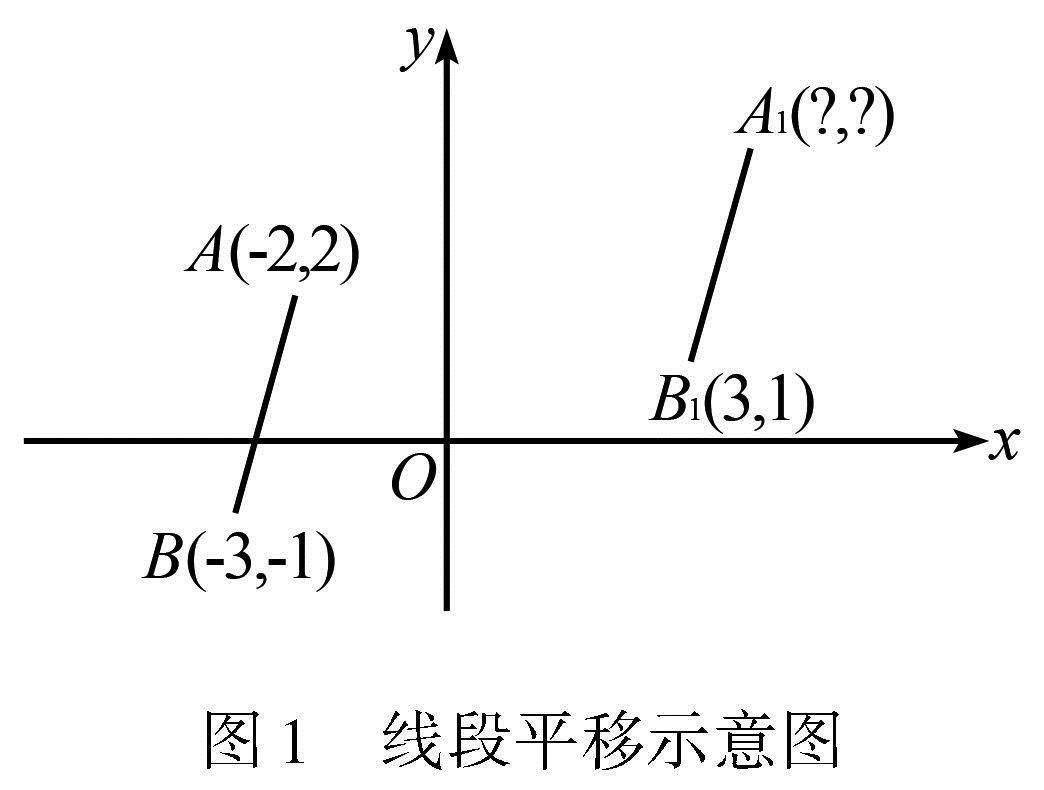
問題2 如圖1，將線段AB平移到線段A1B1的位置，則點A1的坐標(biāo)是.

學(xué)生運用平面直角坐標(biāo)系中點的平移規(guī)律進行解答，有多種解法.下面展示其中一種解法.

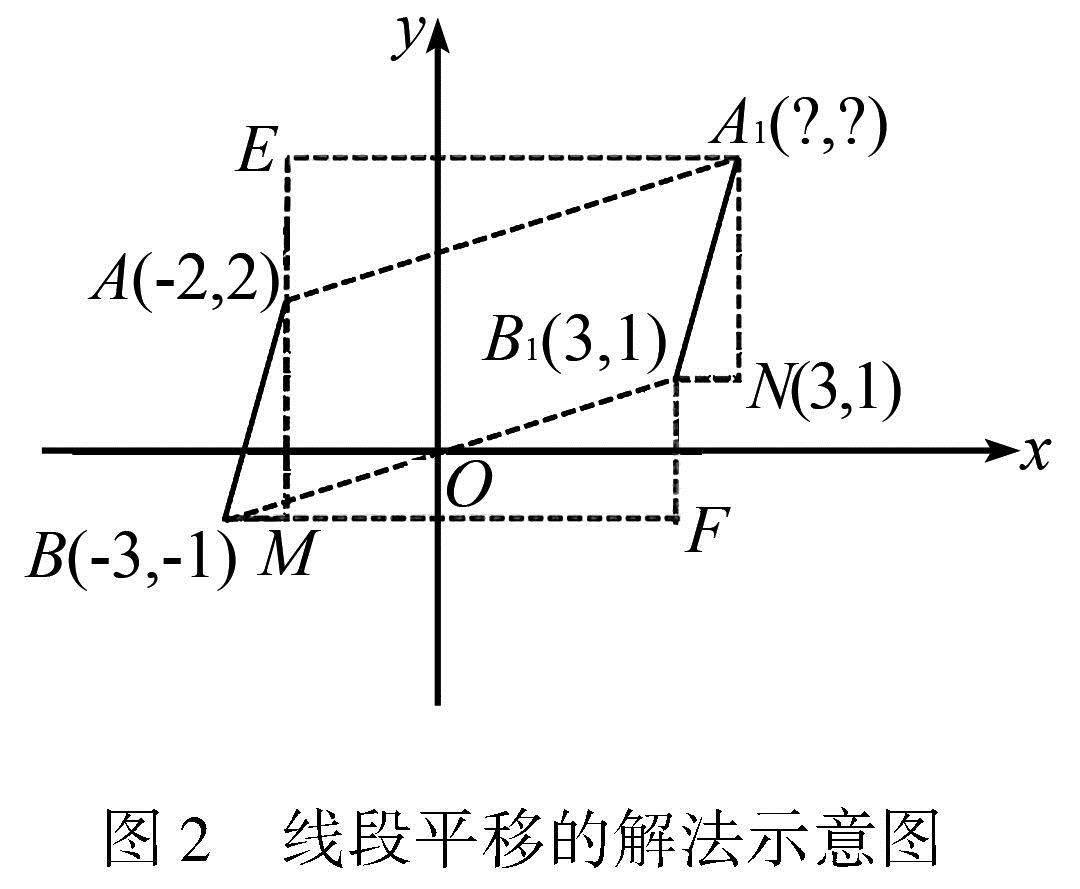
如圖2，連接AA1， BB1，分別過點A作x軸的垂線，過點A1作y軸的垂線相交于點E，過點B作y軸的垂線，過點B1作x軸的垂線相交于點F.易得△AA1E≌△B1BF.設(shè)A1的坐標(biāo)是（x，y），則A1E=BF，x -（-2）=3-（-3），求得x=4，同理可得y=4.所以點A1的坐標(biāo)為（4，4）.

設(shè)計意圖：學(xué)生回顧平移的有關(guān)性質(zhì)，可得AB∥A1B1， AA1∥BB1，且AB=A1B1，AA1= BB1，四邊形ABB1A1是平行四邊形，為后面的問題作鋪墊 [1].

2 規(guī)律探究

問題3 如果有一個任意的平行四邊形ABCD，頂點坐標(biāo)分別A（xA，yA），B（xB，yB），C（xC，yC），D（xD，yD），這四個頂點的橫縱坐標(biāo)之間分別有什么樣的數(shù)量關(guān)系？

解析 過點A、D分別作x、y軸的垂線交于點E，過點B、C分別作x、y軸的垂線交于點F，易得△AED≌△CFB，所以DE=BF，AE=CF，即 xD-xA=xC-xB，yD-yA=yC-yB. 同理可得

追問1 反過來，如果有一個四邊形ABCD，它的四個頂點的坐標(biāo)滿足上面的數(shù)量關(guān)系，這個四邊形ABCD是平行四邊形嗎？

追問2 通過證明發(fā)現(xiàn)它們是一個等價于的關(guān)系.大家再仔細觀察，上述兩個方程組有什么共同特征？

追問3 同學(xué)們能用文字語言總結(jié)此結(jié)論嗎？

性質(zhì)：平面直角坐標(biāo)系中，平行四邊形兩組相對頂點的 橫坐標(biāo)之和相等，縱坐標(biāo)之和也相等．

判定：平面直角坐標(biāo)系中，兩組相對頂點的橫坐標(biāo)之和相等，縱坐標(biāo)之和也相等的四邊形是平行四邊形，不妨稱之為“對點法”.

設(shè)計意圖：從平移線段開始引導(dǎo)學(xué)生觀察平行四邊形坐標(biāo)間的關(guān)系，借助問題2的探究方法和思路，開展問題3的探究，歸納出一般結(jié)論，滲透化歸，從特殊到一般等思想方法，得到的方程組簡潔、對稱性好，為結(jié)論的靈活應(yīng)用創(chuàng)造了良好條件[2].

3 結(jié)論應(yīng)用

3.1 類型1：“三定一動”型

例1 如圖3，已知拋物線y=x2-x-2與x軸的交點為A、B，與y軸的交點為C，點P是平面內(nèi)一點，判斷有幾個位置能使以點P、A、B、C為頂點的四邊形是平行四邊形，請寫出相應(yīng)的坐標(biāo)．

解析 根據(jù)題意求出A（-1，0），B（2，0），C（0，-2），設(shè)點P的坐標(biāo)為（x，y），分三種情況討論.

思路小結(jié)：第一步，求出定點，根據(jù)條件用含字母的式子表示動點的坐標(biāo)，即設(shè)點；第二步，根據(jù)對應(yīng)頂點分類，利用對點法列方程組求解，即求點；第三步，畫出幾何圖形，檢驗結(jié)果的正確性，即驗點.

設(shè)計意圖：通過應(yīng)用“對點法”，學(xué)生體驗到從代數(shù)角度解決幾何問題的優(yōu)點，思路清晰，分類明確，不用借助圖形，直接利用頂點間的關(guān)系列出方程組求出結(jié)果.第三步驗點，讓學(xué)生感受幾何圖形的直觀，整個過程生動體現(xiàn)了華羅庚先生所說的“數(shù)缺形時少直觀，形少數(shù)時難入微.”

3.2 類型2：“兩定兩動”型

例2 （2022年攀枝花中考試題改編）如圖4，二次函數(shù)y=x2-2x的圖象與x軸交于O、A兩點，且二次函數(shù)的最小值為-1，點M（1，m）是其對稱軸上一點，y軸上一點B（0，1）．在二次函數(shù)圖象上是否存在點N，使以A、B、M、N為頂點的四邊形是平行四邊形？若存在，直接寫出所有符合條件的點N的坐標(biāo)，若不存在，請說明理由．

解析 根據(jù)條件易得A（2，0），B （0，1），設(shè)M （1，m ），N（n， n2-2n）.分三種情況討論.當(dāng)點N與點A相對，點B與點M相對時，得n+2=0+1， n= -1，n2-2n=3所以N（-1，3）；當(dāng)點N與點B相對，點A與點M相對時，得n+0=1+2， n=3，n2-2n=3，所以N（3，3）；（3） 當(dāng)點N與點M相對，點A與點B相對時，得n+1=0+2， n=1，n2-2n=-1，所以N（1，-1）.綜上所述，滿足條件的點N有三個，分別為（-1，3），（3，3），（1，-1）.

設(shè)計意圖：進一步熟練對點法的應(yīng)用，不用畫出圖形，直接根據(jù)例1的思路小結(jié)分類求解，并且此題求點N的坐標(biāo)，只要求出n的值即可.根據(jù)條件不需要列出方程組，只需利用對點法中相對頂點的橫坐標(biāo)之和相等列出第一個方程就能得出結(jié)果.

3.3 類型3：“四動”型

練習(xí) 平面直角坐標(biāo)中，y = 0.5x2+ x - 4與y軸相交于點B （0，-4），點P是拋物線上的動點，點Q是直線y = - x上的動點，判斷有幾個位置能使以點P、Q、B、O為頂點的四邊形為平行四邊形，寫出相應(yīng)的點Q 的坐標(biāo).

設(shè)計意圖：在應(yīng)用結(jié)論環(huán)節(jié)，設(shè)計了“三定一動”和“兩定兩動”型問題，常規(guī)方法對學(xué)生而言是有一定困難的.利用對點法，直接設(shè)點列方程組求解點的坐標(biāo)更加直接，通過兩個例題總結(jié)了設(shè)點、求點的解題思路，最后拓展到四個動點的情況仍可用這樣的方法解決.

4 拓展延伸

例3 （2022年隨州中考試題改編）如圖5，在平面直角坐標(biāo)系xOy中，拋物線y=-x2-2x+3與x軸分別交于點A（-3，0）和點B（1，0），與y軸交于點C，對稱軸為直線x=-1，且OA=OC，P為拋物線上一動點．設(shè)M為拋物線對稱軸上一動點，當(dāng)P，M運動時，在坐標(biāo)軸上是否存在點N，使四邊形PMCN為矩形？若存在，直接寫出點P及其對應(yīng)點N的坐標(biāo)；若不存在，請說明理由．

解法從略，請讀者自行探究.

設(shè)計意圖：矩形的存在性問題有一定的難度，此題在對點法求平行四邊形存在性的基礎(chǔ)上再根據(jù)對角線相等的平行四邊形是矩形的性質(zhì)，利用勾股定理列方程，解出方程組即可.

5 教學(xué)思考

5.1 建構(gòu)知識，理清脈絡(luò)

二次函數(shù)背景下特殊四邊形的存在性問題具有一定的挑戰(zhàn)性，為了突破這一難點，我們歸納出“對點法”的解題策略.平行四邊形的存在性問題中由“一動”“兩動”到“四動”三個問題層層推進，讓學(xué)生體會到方法的一致性和思維的連貫性.從平行四邊形到矩形的例題設(shè)計注重層次性、階梯性，始終有意識地挖掘?qū)W生的最近發(fā)展區(qū)，讓難度螺旋式遞進，遵循“高立意，低起點，深研究”的設(shè)計原則，讓不同學(xué)習(xí)水平的學(xué)生都能從中獲得進步和發(fā)展.

5.2 思想立意，提升思維

在中考復(fù)習(xí)中，數(shù)學(xué)思想方法的滲透也是教學(xué)的重任，本專題中運用了轉(zhuǎn)化，化歸、從特殊到一般、分類討論、數(shù)形結(jié)合等思想對問題展開研究.比如，借助問題2的探究方法和思路開展問題3的探究，歸納出一般結(jié)論、滲透化歸、從特殊到一般、數(shù)學(xué)建模等數(shù)學(xué)思想.

參考文獻：

［1］ 中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）[M].北京：北京師范大學(xué)出版社，2022.

[2] 楊少輝.二次函數(shù)中構(gòu)造平行四邊形的解題策略[J].新課程（中），2019（02）：94.