以史為鑒,重構課堂
王保紅 梁詩晗

1 問題提出
《普通高中數學課程標準(2017年版2020年修訂)》在課程結構中明晰了“數學文化融入課程內容”的要求,闡明了“數學的思想、精神、語言、方法、觀點,以及它們的形成和發展”是數學文化的重要內容.
“指數函數與對數函數”是高中數學教學的核心內容之一.課標要求“收集、閱讀對數概念的形成與發展的歷史資料,撰寫小論文,論述對數發明的過程以及對數對簡化運算的作用”等不作為考試內容的要求.人教A版高中數學新教材必修第一冊“對數的概念”兩處融入了數學史.“閱讀與思考”中,“對數的發明”在于培養學生創新思維,使學生通過數學閱讀加深對數學知識的深層次理解.“文獻閱讀與數學寫作”中,“對數概念的形成與發展”是新增設的版塊,目的是希望學生自主了解數學知識形成與發展的脈絡,感受數學文化.本文中以“對數的概念”教學為例,力求在教學中適當融入數學史,以期為高中數學教學提供參考.
2 梳理對數的發展歷史
2.1 對數思想的萌芽
約公元前1700年巴比倫泥版上出現了類似解指數方程的題目.15世紀法國數學家許凱(N.Chuquet)在《算術三部》提出了解指數方程的問題,還列出了等比和等差數列,即1,2,4,8,16,……,1 048 576和0,1,2,3,4,……,20,指出數列對應關系:上一列數的乘除運算結果對應下一列數的加減運算結果.
16世紀涌現出了許多研究等比數列乘法法則的數學家.德國數學家斯蒂菲爾(M.Stifel)提出了四條乘法法則,即幾何級數中的乘法、除法、乘方、開方與算術級數的加法、減法、乘法、除法對應,還將法則推廣到負指數,形成雙數列對應關系.
天文、航海等領域要求大數運算.而想要算出一個復雜的數據,需長達幾年的時間.因此,迫切需要改進數字計算方法,以提高計算速度和準確度.
2.2 對數方法和思想的產生
蘇格蘭數學家納皮爾(J.Napier)研究大數運算,最終發明了對數,并將對數(logarithm)意為“比的數”.1614年出版的《奇妙的對數定律說明書》標志著對數的誕生.英國數學家布里格斯(H.Briggs)與納皮爾商定了“曠世之約”:1的對數為0,10的對數為1.布里格斯制作
的常用對數表更容易算出數值,將底數為10的對數稱其為常用對數,底數概念也由此誕生.法國數學家拉普拉斯(P.S.Laplace)評價道:“因為省時省力,對數倍增了天文學家的壽命.”
瑞士儀器制造者比爾吉(J.Burgi)也獨立發現了對數并用它來造表.1620年他出版了《等差數列和等比數列》,盡管那時納皮爾發明的對數已聞名歐洲.18世紀瑞士數學家歐拉發現指數與對數的互逆關系,指出“對數源于指數”.
2.3 自然對數的由來
使用常用對數時發現N與其對數并非同時均勻增長,為了尋求能使兩邊對稱的底數,讓式子化繁為簡,發現若以e作底數最“自然”,符合數學的對稱美和簡潔美.故以e為底的對數叫“自然對數”,亦定義logeN=ln N,在科技、經濟中有廣泛應用.
3 基于數學史的對數概念教學
3.1 教學思路
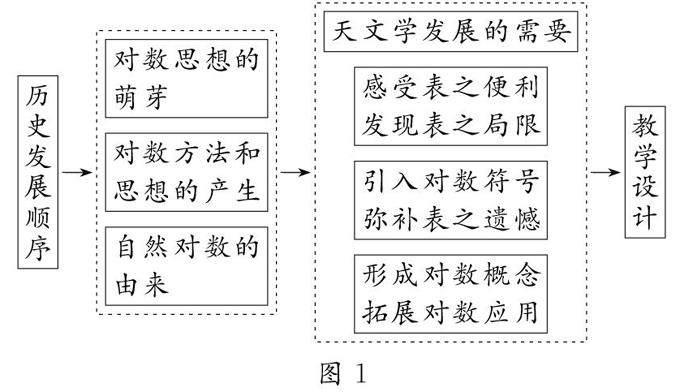
依據對數歷史,整體采用重構式的設計(如圖1),借鑒對數歷史,追溯思想起源,呈現知識自然發生的過程.
3.2 重構對數概念的數學課堂
3.2.1 天文學發展的需要
例1?隨著科技的發展,人類對宇宙的探索愈加深入.天文學定義,光在真空中的速度為299 792.468 km/s,一年的總秒數是31 536 000 s,能否動筆求出一光年的值?
(列式為299 792.468×31 536 000=?)
師:介紹對數產生的原因.該如何簡化運算?
設計意圖:利用生活實例創設情境,使學生感受大數運算的不易,由此產生探究簡化大數運算的想法.
3.2.2 感受表之便利,發現表之局限
例2?展示斯蒂菲爾雙數表(表1),讓學生觀察規律.
師:第二行中后一個數是前一個數的兩倍.若第1行表示2的指數,則第2行表示其對應的冪.16世紀數學家斯蒂菲爾在研究上表時,把第一行的各項稱為“指數”.他還發現第一行指數相加得到其乘積的指數,指數相減得到其商的指數.
師:求32×512,先找到32和512在數表中對應的第一行的數.即32對應5,512對應9;將二者相加,即5+9=14;再找到14對應的下一行數為16 384.
師:按照規律,能否快速求出下列各式子的值?
16×1 024;8 192÷32;643;81×729.
上面有些數并不能從數表中查到,該如何解決?發現81與729兩個數都能變成以3為底的冪的形式,但查不到.法國數學家許凱也曾遇到這樣的問題,而且是在斯蒂菲爾之前.相對于自然數列而言,他研究的雙數表可表示2或3的指數.
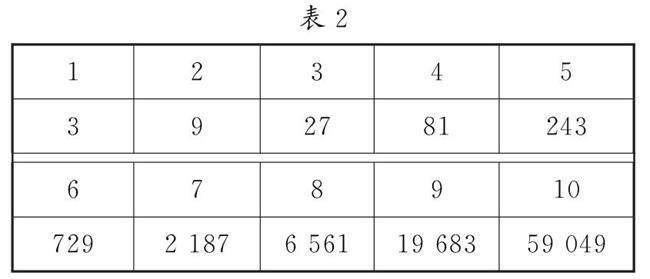
例3?請大家根據許凱雙數表(表2)完成計算.
師:如果算式是其他數呢?由于第二行相鄰兩項的差值越來越大,數便難以找到.當時的天文學家對此非常苦惱.于是數學家開始制作更加詳細的數表.其中貢獻最大的是納皮爾(可介紹納皮爾與對數).例1該怎么解決?
找到299 792.468和31 536 000分別對應的數,先求和再查表.令2x=299 792.468,2y=31 536 000.
追問:整數可以通過查表得到,小數點后幾位怎么算?如何得到精確值?
設計意圖:根據乘法法則,讓學生經歷簡化運算的過程,感受查表的便利.講述納皮爾貢獻,培養學生科學精神和探究意識.利用提示語啟示學生發現對數表的局限性,引出新知識.
3.2.3 引入對數符號,彌補表之遺憾
師:之前是否遇到過類似的難題?初中是如何計算x2=2的?在學習“[YY(]1[YY)]”后,我們解決了非完全平方數的平方根問題.同理,當現有知識不足以解決問題時,需要創造新的符號來表示.數學家將對數“logarithm”簡寫為“log”.這樣就解決了像例1中這種“天文數字”的計算.引用數學家對對數的評價.
設計意圖:借助舊知,引入新知.體會引入符號的必要性,彌補數表局限的遺憾.
3.2.4 形成對數概念,拓展對數應用
師:觀察對數,思考它與指數有何關系?
追問:二者可以互相轉化,即對數logaN與指數互逆.對數中a的取值范圍是什么?
回顧指數概念.得到對數概念:一般地,若ax=N(a>0,且a≠1),那么數x稱為以a為底N的對數,記作x=logaN,其中a叫作底數,N叫作真數.當a>0且a≠1時,ax=Nx=logaN,這是互化公式.計算方便,又能比較大小.0和負數沒有對數.
利用數學家軼事講解常用對數.把常用對數log10N記作lg N.總結:logaa=1,loga1=0,log10N=lgN.由常用對數引出自然對數.
設計意圖:暗示學生指數與對數存在互逆關系;滲透數學史,將知識自然呈現;強調一般對數與常用對數、自然對數之間的轉化.
3.2.5 鞏固練習,總結課堂
(1)在巴比倫泥版上有一道復利題目1.2x=2,請求解.
(2)將指數式化為對數式,對數式化為指數式(教材例題).
設計意圖:幫助學生整理思路,感受對數在簡化運算方面的作用,總結現實應用.
4 總結與反思
數學史對于數學教育有重要意義.數學史可以幫助學生清除認知障礙,同時數學史也是一面鏡子,把當時思想的碰撞反映到數學知識的學習中.對教師而言,將數學史融入數學教學,可以幫助教師根據學生認知障礙設計教學,提升教書育人的能力,提升數學素養.對學生而言,可以幫助他們了解知識的由來與發展,理解數學知識,體會其中蘊含的思想,提升科學精神,培養數學核心素養.

