淺談初中統計學核心素養的培養
孫娜
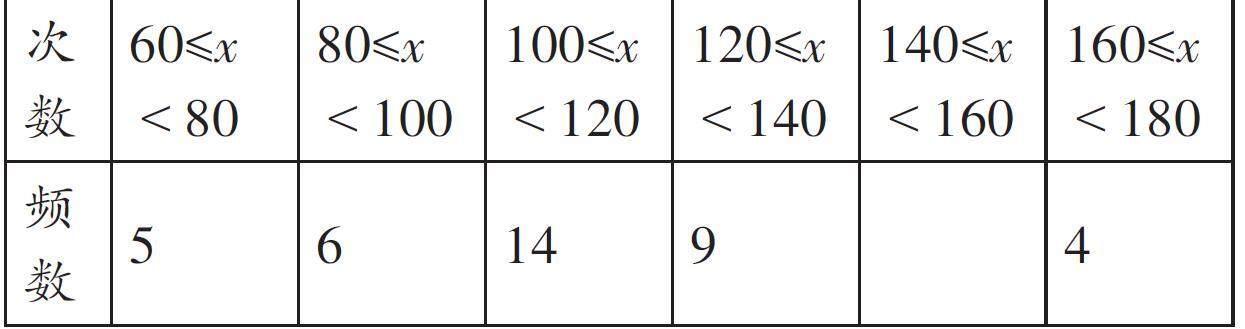
隨著新課程標準的實施,統計觀念不斷得到強化,中考中統計知識的考查已由以往注重技能的考查向注重觀念考查轉變。要求能正確理解和掌握平均數、眾數、中位數、極差、方差、標準差等特征量的意義,能夠結合實際問題的需要有效地表達數據特征,會根據數據的分析作出合理的預測。不僅強調統計圖表信息的表示,而且強調統計圖表的信息交流和問題的轉換。解決這類問題,要讀懂題目的意思,在準確分析特征量的基礎上作出合理的判斷,細心地求解和畫圖,有些實際問題背景知識的掌握還要靠平時生活經驗積累,這就是說“數學就在我們身邊”。
考點一:數據收集方式的選擇
以下問題,不適合用全面調查的是()
A.了解全班同學每周體育鍛煉的時間
B.鞋廠檢查生產的鞋底能承受的彎折次數
C.學校招聘教師,對應聘人員面試
D.黃河三角洲中學調查全校753名學生的身高
考點:全面調查與抽樣調查
分析:由普查得到的調查結果比較準確,但所費人力、物力和時間較多,而抽樣調查得到的調查結果比較近似。
點評:本題考查了抽樣調查和全面調查的區別,選擇普查還是抽樣調查要根據所要考查的對象的特征靈活選用,一般來說,對于具有破壞性的調查、無法進行普查、普查的意義或價值不大時,應選擇抽樣調查,對于精確度要求高的調查,事關重大的調查往往選用普查。
考點二:計算一組數據的平均數,中位數,眾數,極差,方差
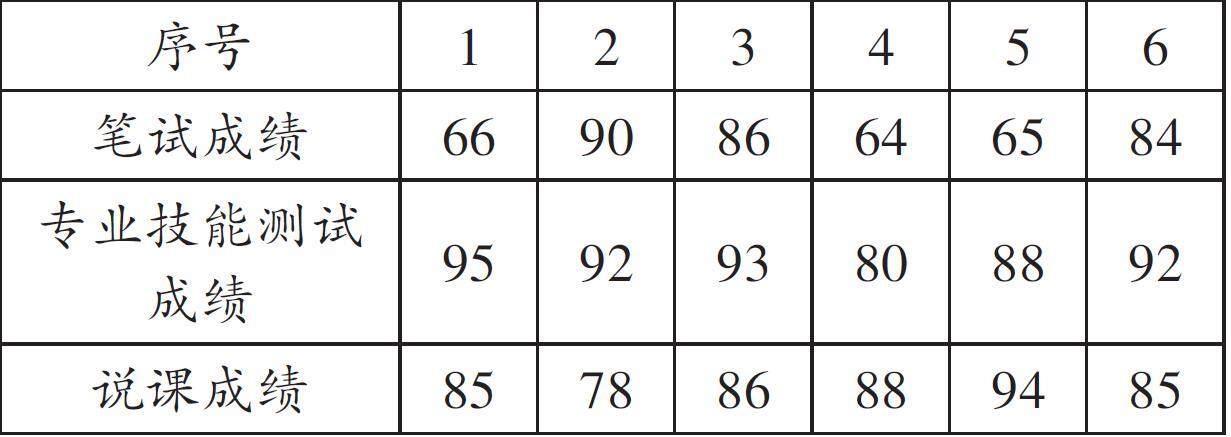
“十年樹木,百年樹人。”教師的素養關系到國家的未來。我市某區招聘音樂教師采用筆試、專業技能測試、說課三種形式進行選拔,這三項的成績滿分均為100分,并按2:3:5的比例折合納入總分,最后,按照成績的排序從高到低依次錄取。該區要招聘2名音樂教師,通過筆試、專業技能測試篩選出前6名選手進入說課環節,這6名選手的各項成績見下表。
(1)筆試成績的極差是多少?
(2)寫出說課成績的中位數、眾數;
(3)已知序號為1,2,3,4號選手的成績分別為84.2分,84.6分,88.1分,80.8分,請你判斷這六位選手中序號是多少的選手將被錄用?為什么?
考點:加權平均數;中位數;眾數;極差。
專題:圖表型。
分析:(1)根據極差的公式:極差=最大值-最小值求解即可。
(2)根據中位數和眾數的概念求解即可。
(3)根據加權平均數的計算方法求出5號和6號選手的成績,進行比較即可。
點評:這兩個題主要考查了極差、中位數、平均數、加權平均數和眾數的知識,屬于基礎題,比較容易解答,關鍵是熟練掌握其計算方法。
考點三:用樣本估計總體
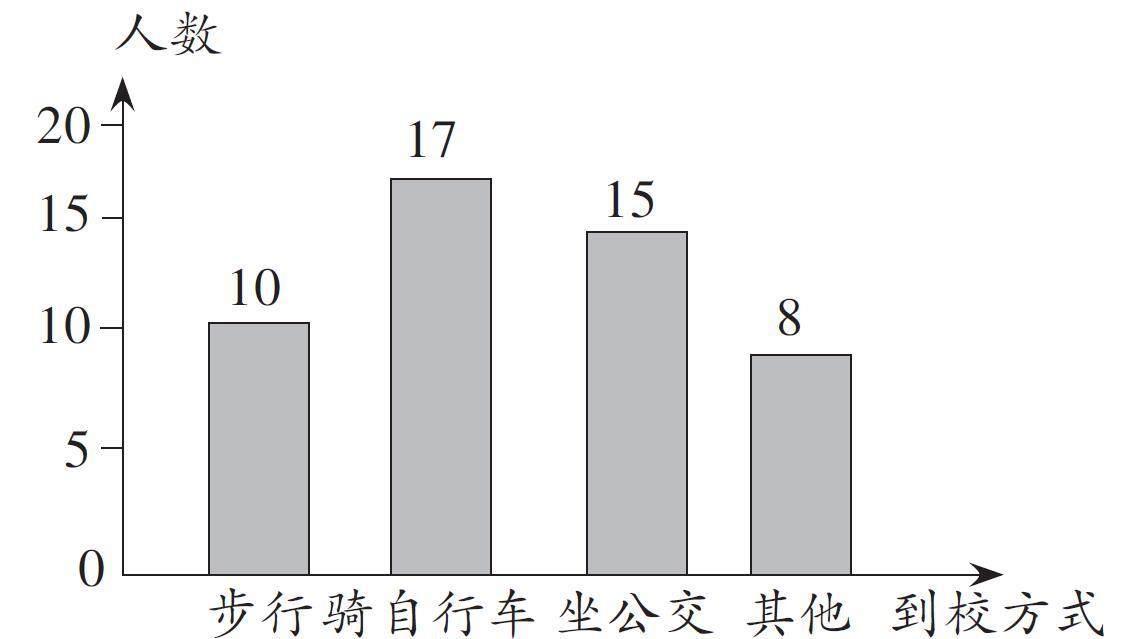
某初中學校共有學生720人,該校有關部門從全體學生中隨機抽取了50人,對其到校方式進行調查,并將調查的結果制成了如圖所示的條形統計圖,由此可以估計全校坐公交車到校的學生有? ? ? ? ? ?人。
考點:用樣本估計總體;條形統計圖;加權平均數。
專題:數形結合。
分析:先求出50個人里面坐公交車的人數所占的比例,然后即可估算出全校坐公交車到校的學生。
點評:此題考查了用樣本估計總體的知識,解答本題的關鍵是根據所求項占樣本的比例,屬于基礎題,難度一般。
考點四:統計圖表的綜合運用
某校九年級二班的學生植樹節開展“植樹造林,綠化城市”的活動,活動結束后,該班植樹情況的部分統計圖如下所示,那么該班的總人數是40人。
考點:條形統計圖;扇形統計圖。
專題:應用題。
分析:從條形統計圖得到植樹4株的人數為5人,從扇形統計圖得植樹4株的人數占總人數的12.5%,則該班的總人數=5÷12.5%。
點評:本題考查了條形統計圖:條形統計圖反映了各小組的總數;也考查了扇形統計圖:扇形統計圖反映各小組所占總體的百分比。
考點五:頻數(率)分布直方圖
某中學積極開展跳繩活動,體育委員統計了全班同學1分鐘跳繩的次數,并列出了頻數分布表。
(1)跳繩次數x在120≤x<140范圍的同學占全班同學的20%,在答題卡中完成上表;
(2)畫出適當的統計圖,表示上面的信息。
考點:頻數(率)分布表;頻數(率)分布直方圖。
分析:(1)根據跳繩次數x在120≤x<140范圍的同學占全班同學的20%,求出總人數,再用總人數減去各段的頻數,即可求出在140≤x<160的頻數;
(2)根據表中提供的數據,從而畫出直方圖即可。
點評:此題考查了頻率分布直方圖,解題的關鍵是根據頻數、頻率之間的關系,求出總人數,要能從統計表中獲得有關信息,列出算式。

