一道高三統(tǒng)測(cè)解析幾何試題的命制、測(cè)評(píng)結(jié)果及分析
尤 裕 (江蘇省梅村高級(jí)中學(xué) 214112)
嚴(yán) 鵬 (江蘇省鎮(zhèn)江崇實(shí)女子中學(xué)·茅以升中學(xué) 212004)
1 命題背景
從以往全國(guó)高考數(shù)學(xué)卷來(lái)看,解析幾何命題的結(jié)構(gòu)嚴(yán)謹(jǐn),考查學(xué)生的能力全面,不僅考查學(xué)生的計(jì)算能力,還考查轉(zhuǎn)化與化歸的思想,以及對(duì)整體和部分的協(xié)調(diào)性的把握.2022年全國(guó)甲卷(理)第20題、2022年北京卷第19題、2021年全國(guó)卷第21題、2020年全國(guó)卷Ⅰ(文)第21題,均以直線的斜率為考查背景,所以本次高三統(tǒng)測(cè)解析幾何試題的命制以斜率這個(gè)熱點(diǎn)問(wèn)題為背景,對(duì)學(xué)生的數(shù)學(xué)運(yùn)算、邏輯推理等核心素養(yǎng)進(jìn)行了檢驗(yàn).試題主要考查了直線與橢圓的位置關(guān)系,旨在體現(xiàn)解析幾何用代數(shù)方法解決幾何問(wèn)題的基本思想.
2 試題及解析
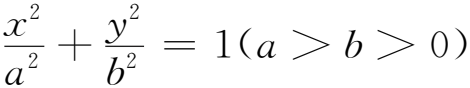
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)若經(jīng)過(guò)點(diǎn)T(1,0)的直線交橢圓C于A,B兩點(diǎn),點(diǎn)P為直線x=4上任意一點(diǎn),證明:kPA,kPT,kPB成等差數(shù)列.
解析 本題的思維導(dǎo)圖如圖1所示.

圖1

圖2

(2) ①當(dāng)直線AB斜率為0或不存在時(shí),點(diǎn)A,B的坐標(biāo)易求得,顯然kPA+kPB=2kPT.


綜合①②,kPA,kPT,kPB成等差數(shù)列.
本題考查了橢圓的簡(jiǎn)單性質(zhì)及方程思想、直線與橢圓位置關(guān)系的相關(guān)問(wèn)題,還考查了計(jì)算能力、轉(zhuǎn)化思想及推理論證能力.常規(guī)思路是直線方程與橢圓方程聯(lián)列、消元、化簡(jiǎn),然后應(yīng)用根與系數(shù)的關(guān)系建立方程,解決相關(guān)問(wèn)題.
3 結(jié)果及分析
考完后,統(tǒng)計(jì)班級(jí)本題的得分情況,結(jié)果見(jiàn)表1.得分集中在5~6分,均分6.375,高分率8.3%.

表1 第22題得分情況
第(1)題滿分的學(xué)生與第(2)題是否完成的相關(guān)性為23.6%,說(shuō)明完成第(1)題對(duì)第(2)題是否能做對(duì)關(guān)系不大.從原始數(shù)據(jù)來(lái)看,第(2)題滿分的學(xué)生,第(1)題均為滿分,第(2)題與總分的相關(guān)性為95.5%,說(shuō)明做對(duì)第(2)題對(duì)本題得11分或12分有很大的相關(guān)性.
在解決本題時(shí)學(xué)生存在的主要問(wèn)題有:(1)沒(méi)有討論斜率不存在的情況;(2)在處理(*)式時(shí)不敢動(dòng)手化簡(jiǎn),在分子的展開(kāi)、化簡(jiǎn)和代入時(shí)產(chǎn)生計(jì)算錯(cuò)誤.

4 反思與實(shí)踐
學(xué)會(huì)學(xué)習(xí)比學(xué)會(huì)知識(shí)更重要,數(shù)學(xué)核心素養(yǎng)在學(xué)生身上的一個(gè)重要表現(xiàn)就是“會(huì)學(xué)習(xí)”.學(xué)生的數(shù)學(xué)核心素養(yǎng)需要在數(shù)學(xué)活動(dòng)過(guò)程中,通過(guò)一次次專心的觀察和分析、一次次有序的操作和驗(yàn)證、一次次細(xì)心的推演和計(jì)算、一次次大膽的猜測(cè)和判斷、一次次縝密的推理和論證,還有一次次與同學(xué)和老師的討論、質(zhì)疑、交流等,一點(diǎn)一點(diǎn)建立、積累和提升起來(lái),這些活動(dòng)經(jīng)驗(yàn)可以成為學(xué)生思維的重要載體.
因此,數(shù)學(xué)教學(xué)中要注意加強(qiáng)數(shù)學(xué)學(xué)習(xí)方法的指導(dǎo),幫助學(xué)生積累基本的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn),使學(xué)生學(xué)會(huì)知識(shí)的探究和應(yīng)用,學(xué)會(huì)數(shù)學(xué)的學(xué)習(xí).下面提供兩個(gè)練習(xí)供解題實(shí)踐.

(1)求E的方程;
(2)證明:直線CD過(guò)定點(diǎn).

(1)當(dāng)l與x軸垂直時(shí),求直線AM的方程;
(2)設(shè)O為坐標(biāo)原點(diǎn),證明:∠OMA=∠OMB.

