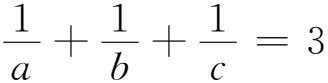
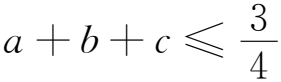用一種代換方法證明三元不等式
孫 紅 (江蘇省灌云高級(jí)中學(xué) 222200)

1 性質(zhì)
已知x,y,z>0,且x+y+z+2=xyz,則
性質(zhì)1xyz≥8.
性質(zhì)2x+y+z≥6.
性質(zhì)3xy+yz+zx≥2(x+y+z).


(2)由條件x+y+z+2=xyz及性質(zhì)1,得x+y+z=xyz-2≥6.
2 應(yīng)用
為了代換方法的統(tǒng)一,對(duì)以下部分例題中的符號(hào)進(jìn)行了改寫.
2.1 約束條件x+y+z+2=xyz的不等式證明


例2(《數(shù)學(xué)通訊》2016年第3期問題250)設(shè)x≥1,y≥1,z≥1,且x+y+z+2=xyz,求證:3(x+y+z)≥xy+yz+zx+6.

例3(2019年奧地利數(shù)學(xué)奧林匹克國(guó)家級(jí)決賽)設(shè)正實(shí)數(shù)x,y,z滿足x+y+z+2=xyz,證明:(x+1)(y+1)(z+1)≥27.






評(píng)注前3個(gè)例題利用條件x+y+z+2=xyz的等價(jià)形式簡(jiǎn)化了證明過程,后2個(gè)例題通過代換方法轉(zhuǎn)化為比較容易證明的不等式.
2.2 無約束條件的不等式證明



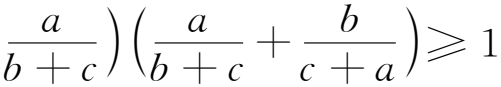





(2)作代換a=cotAcotB,b=cotBcotC,c=cotCcotA(A,B,C為銳角三角形ABC的內(nèi)角),并注意到三角恒等式cotAcotB+cotBcotC+cotCcotA=1,則由例8可得

3 代換方法的延伸
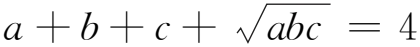
例9(2015年希臘數(shù)學(xué)奧林匹克)已知a,b,c>0,且ab+bc+ca+2abc=1,求證:4a+b+c≥2.




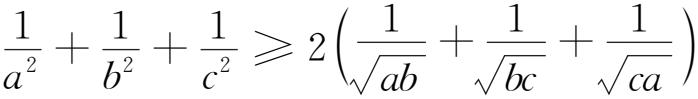



例13(《中等數(shù)學(xué)》2019年第3期問題613)已知正數(shù)a,b,c滿足a2+b2+c2+abc=4,求證:a2b2+b2c2+c2a2+abc≤4.