T-S模糊系統的自觸發有限時間H∞控制
劉曉迪
(江南大學 輕工過程與先進控制教育部重點實驗室,江蘇 無錫 214122)
0 引言
非線性在各種實際系統中廣泛存在,這給穩定性分析和合成帶來了更多的困難和復雜性。T-S模糊模型作為一種非常典型的復雜動態系統模糊模型,通過使用“IF-THEN”規則,將復雜的非線性問題轉化為不同的小線段上的問題,從而使得復雜的非線性系統更容易被分析。T-S模糊模型已經成為處理非線性系統的穩定性分析及控制器綜合的強有力工具,且已被成功應用于多種實際控制問題中,如汽車的防抱死制動系統與主動懸架系統的集成控制[1]、攪拌反應釜系統的性能控制[2]、主從式機器人的適應性的增強[3]等。
然而目前關于T-S模糊的研究大都集中在李亞普諾夫漸近穩定性上,漸近穩定只能夠確保系統的穩態性能良好,但是系統中的某些暫態性能卻未能體現。在實踐中,系統在有限時間間隔內的行為也非常重要。文獻[4]引入有限時間概念,并提出了一個有限時間的控制器設計標準。此后,許多學者參與T-S模糊系統有限時間問題的研究[5-8],研究有限時間控制具有很重要的實際意義。
但上述文獻控制器設計過程中,其狀態向控制器的傳輸通常是連續的。在某些情況下,當控制目標實現時,無需在保持系統性能時依舊每次都傳輸狀態,從而造成冗余傳輸,這就導致了資源的浪費和低效率。造成這一缺點的主要原因是,更新頻率是由采樣周期決定的,通常假設采樣周期是一個較小的值,與系統狀態無關。因此,大量的冗余信息將被傳輸和更新。為了解決這一問題,文獻[9]提出了一種事件觸發控制方案,有效地減少傳輸資源。近年來,人們對事件觸發機制下的T-S模糊系統分析和控制做了大量的工作[10-13]。但是,其檢測機制的被動性決定了其必須實時監測觸發條件,會增大系統的執行代價。而自觸發控制是根據當前的狀態測量值,計算出控制律的下一個更新時刻,進一步節省資源。自觸發控制也因此得到了越來越多的關注[14-18]。文獻[19]利用事件觸發控制和自觸發控制實現線性系統的有限時間穩定。文獻[20]利用T-S模糊模型針對一類開關非線性系統設計了一種事件觸發通信方案,討論了其有限時間耗散控制問題。文獻[21]研究了一種在多頻率范圍限制下的馬爾可夫跳躍系統的自觸發有限時間控制策略。
事件觸發控制都需要事件觸發器實時監控系統狀態和測量誤差。這在有些情況下很難實現且會造成額外計算資源損耗。因此有必要研究自觸發控制。同時,關于T-S模糊系統通過自觸發策略實現有限時間控制的文獻非常稀少,這激發了我們的研究興趣。
基于以上討論,本文研究T-S模糊系統的自觸發有限時間H∞控制問題。主要貢獻為:
針對T-S模糊系統引入一種自觸發方案,考慮參數不確定性和有界干擾對系統的影響,結合所提出的自觸發機制,建立了一個基于自觸發機制的連續時間T-S模糊系統模型。較事件觸發方案而言,自觸發方案不需要額外的硬件來監測觸發條件,合理地減少計算資源及額外硬件資源。考慮有限時間間隔內的行為,使系統狀態在固定的有限時間間隔內不超過一定界限的同時滿足所期望的H∞性能指標。同時本文所提到的自觸發機制避免了芝諾行為的發生,并且提供理論證明。
1 問題描述
考慮如下連續時間非線性系統:
(1)
其中:x(t)為系統狀態,u(t)為控制輸入,引入一個已知的非線性函數f(x(t))來描述其非線性特性。通過采用模糊理論的方法將上述非線性系統(1)用以下具有第i條模糊規則的T-S模糊模型來逼近,其第i條規則描述的系統模型為:
Plant rulei:
ifξ1(t) isMi1,and … andξn(t) isMin,then
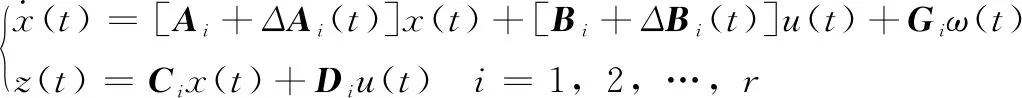
(2)
其中:ξ1,…,ξp為前件變量,x(t)∈nx為系統狀態,u(t)∈nu為控制輸入,ω(t)∈nω為外部擾動且滿足條件ωT(t)ω(t)dt≤W。Ai、Bi、Ci、Di及Gi是適當維數的系數矩陣。r是規則數量,Mij是模糊集,ΔAi(t),ΔBi(t)是系統矩陣中的不確定時變參數,滿足如下形式:
[ΔAi(t)ΔBi(t)]=[HF(t)(E1iE2i)]
i=1,2,…,r
(3)
其中:H,E1i,E2i,i=1,2,…,r是已知的具有適當維數的常數實矩陣,F(t)是滿足F(t)F(t)T≤I的非線性時變矩陣函數,其中I表示適當位數的單位矩陣。則該T-S模糊系統的整體模型為:
(4)
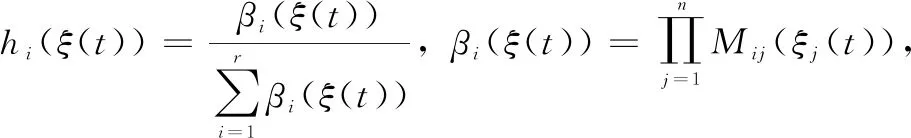
不同于事件觸發控制,自觸發控制提供了一種靈活的周期調整方式。如圖1所示,該機制根據系統動力學知識和當前觸發時刻的狀態信息在自觸發機制中計算下一觸發時刻,并且狀態反饋控制器只與當前觸發時刻的系統信息x(tk)有關。也就是說,只有在觸發時刻控制律才會更新,從而產生比事件觸發控制更長的任務周期。

圖1 自觸發機制原理圖
因此,利用并行分布補償方法,設計具有如下規則的狀態反饋控制器:
Plant rulei:
ifξ1(t) isMj1and … andξn(t) isMjn,
thenu(t)=Kjx(tk),?t∈ [tk,tk+1)
(5)
式中,Kj為局部反饋控制增益矩陣,tk是當前觸發時刻,tk+1是下一觸發時刻,x(tk)是當前觸發時刻的系統狀態。模糊控制器的總體模型為:
(6)
定義e(t)為誤差,且
e(t)=x(tk)-x(t)
(7)
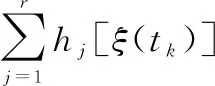

(8)
本文所涉及定義及引理較多,為方便下文討論,在此先給出介紹。
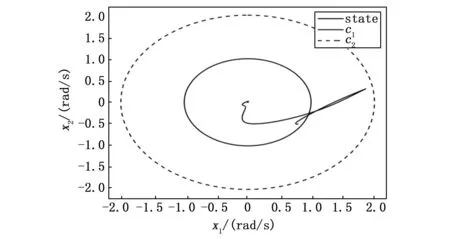
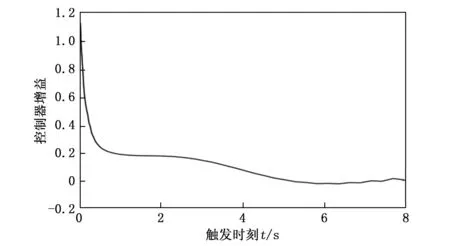
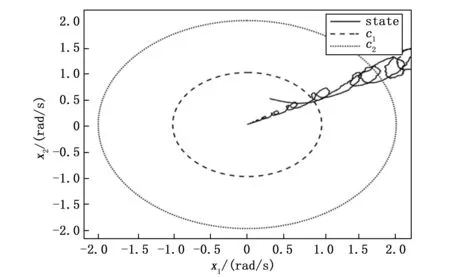
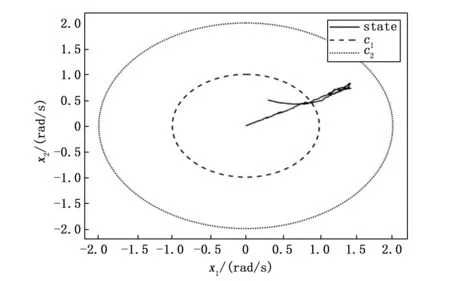
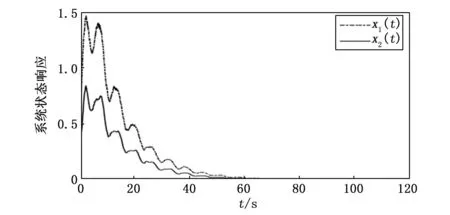
定義1 :對于給定的常數c1,c2,T(c1 xT(0)Rx(0)≤c1?xT(t)Rx(t)≤c2,?t∈[0,T] (9) 則自觸發閉環系統(8)是(c1,c2,T,R,W)有限時間穩定的。 定義2 :對于給定的常數c1,c2,T(c1 xT(0)Rx(0)≤c1?xT(t)Rx(t)≤c2,?t∈[0,T] (10) 則自觸發閉環系統(8)是(c1,c2,T,R,W)有限時間有界。 定義3:給定參數0 (11) 則系統(8)關于(c1,c2,T,R,W)有限時間有界且同時滿足所期望的干擾抑制水平γ。 引理1:對給定的適當維數的矩陣Y,H,E,其中Y是對稱矩陣,F滿足FTF≤I,當且僅當存在一個常數β>0,使得Y+βHHT+β-1EET<0成立時,有Y+HFE+ETFTHT<0。 引理2 :對于任意適維實矩陣X,Y和任意正標量λ>0,下列不等式成立: XTY+YTX≤λXTX+λ-1YTY 注:前文提到的有限時間穩定與通常意義下李雅普諾夫穩定是截然不同的概念。有限時間穩定是指在一個有限的時間區間范圍,系統的狀態軌跡始終能保持在預先給定的界限,它注重研究的是系統的暫態性能。 自觸發控制系統的核心通常包括一個反饋控制器和一個預測何時傳輸數據和更新控制信號的觸發器。觸發器決定傳輸數據之前,兩個觸發間隔之間的控制信號沿用上一觸發時刻的控制信號保持不變,即在此期間不進行數據傳輸和控制信號的更新以達到節約通信資源的目的。然而由于觸發器的存在,使自觸發控制下的閉環系統是一個同時具有連續和離散特征的混合系統,這勢必會增大對系統穩定性分析的難度。 本文主要針對不確定T-S模糊系統進行基于自觸發機制下有限時間的干擾魯棒控制研究,研究主要分為兩步: 1) 針對不確定T-S模糊系統(4)引入自觸發機制,主要任務為設計并推導自觸發間隔函數,使其僅根據系統當前采樣信息決定下一個執行時刻以減少通訊及計算資源的占用。并針對不同的模糊子系統設計不同的觸發閾值、觸發矩陣,顯著提高了設計的靈活性,有效地減輕了通信負擔,直接反映了模糊模型的結構特征。 2) 設計模糊反饋控制器,結合H∞理論、有限時間有界思想,使得自觸發閉環控制系統(8) 具有一個給定的有限時間H∞性能,且保證系統運動軌跡不會超過一定的界限。 在事件觸發控制策略中,常常定義一個事件觸發函數,當且僅當事件觸發函數滿足一定條件時事件觸發/發生,此時更新采樣值。但是對于此條件的檢測往往是需要額外硬件設備進行持續檢測的。 與事件觸發控制相比,自觸發控制是指系統或設備通過內部機制來執行某些操作,不需要外部的觸發信號或指令。此控制方式的一個基本要求是如何設計觸發間隔函數τ(x(tk))。通過表達式tk+1=τ(x(tk))+tk預測下一觸發時刻,從而降低控制的實現成本。 引入下列觸發條件(12),Φi為第i條模糊規則下待求的觸發參數矩陣,0<εi≤1為第i條模糊規則下對應的觸發系數。 eT(t)Φie(t)≥εixT(t)Φix(t) (12) 定理1:對于給定參數β及觸發系數εi,且滿足1-εi(1-β-1)>0,則自觸發控制系統的觸發間隔函數表達式如下: (13) 其中: (14) (15) 若在時間間隔 [tk,tk+1) 系統沒有觸發,由事件觸發條件(12)結合式(7)可知下式成立: eT(t)Φie(t)<εixT(t)Φix(t)< εi[xT(tk)-eT(t)]Φi[x(tk)-e(t)]< εixT(tk)Φix(tk)+εieT(t)Φie(t)- εieT(tk)Φix(tk)-εixT(tk)Φie(tk) (16) 結合引理2,有: eT(t)Φie(t)<εi(1-β-1)eT(tk)Φie(tk)+ εi(1-β)xT(tk)Φix(tk) (17) 不等式(17)可以寫為: 故系統觸發時應該滿足以下條件: (18) 結合不等式(15)、(18),可得: (19) (20) 對不等式(20)兩邊取對數,則可得到自觸發間隔函數關系式(13),證畢。 此外,從自觸發間隔函數關系式(13)可以得出: (21) Zeno行為是事件驅動函數-段時間內被無限次數觸發,排除芝諾行為是事件驅動機制可以使用的重要前提條件。 在實際工業過程中,除了系統在無限時間內的穩態性能外,有時暫態性能尤其重要。實際上,如果一個穩定的系統具有較壞的暫態性能,比如震蕩劇烈、反應遲緩等,將會造成很壞的影響,從而無法滿足工業過程的應用要求。基于這種情況的存在使得在有限時間內約束系統的狀態軌跡成為必要。 本節將自觸發條件與H∞理論相結合,同時考慮有限時間穩定。對自觸發閉環系統(8)進行H∞性能分析,經過嚴格數學推導,得到定理2、定理3。 定理2:如果對于給定參數0<εi≤1,0 (22a) (22b) (22c) 證明:取李亞普諾夫函數為: (23) ζ=[xT(t)eT(t)ωT(t)]不等式(23)可以寫為: ζT+αV(x(t))+eT(t)Φie(t)- εixT(t)Φix(t)+γ2ωT(t)ω(t) (24) 利用引理4對不等式(22a)進行變形,可得: (25) 由不等式(22)、(23),可得如下條件: (26) 對上式兩邊同乘e-αt,則有: d(e-αtV)/dt (27) 對于?t∈[0,T],如下不等式成立: (28) 同時我們有: (29) 結合(28)、(29)兩式,可得: (30) 顯然,由式(30)可看出,對于?t∈[0,T],xT(t)Rx(t) 定義ξ=[xT(t)eT(t)ωT(t)zT(t)] εixT(t)Φix(t)-γ2ωT(t)ω(t)+zT(t)z(t) (31) 結合式(22a)、式(31)以及觸發條件(13),可以得到: 對上式左右兩邊同乘e-αt,并取0到T積分,得到如下不等式: 則有: (32) 由定義3可知,上述不等式成立可確保自觸發控制系統(8)關于(c1,c2,T,R,W)有限時間有界且滿足所期望的H∞性能。 定理2給出的矩陣不等式(22a)~(22c)并不是嚴格意義上的線性矩陣不等式,在編程工具中無法直接求解。 線性矩陣不等式的求解可轉化為凸優化問題的求解,自1988 年Nesterov和Nemirovski提出內點法,并直接用以求解具有線性矩陣不等式約束的凸優化問題,使得求解線性矩陣不等式成為處理控制問題的一種有效手段。將上述不等式進行處理,得到定理3。 Ψii<0,i=1,2,…,r (33a) Ψij+Ψji<0,i (33b) (33c) (33d) (β1+β2)HHT 證明: (34) 結合(2)式及引理1,不等式(34)等價于下式: 上式等價于: (35) 同理,利用引理1對參數不確定項進行上述處理,結合引理2。令Yj=KjQ可得: 顯然,上式等價于下式 (36) 從而式(33a)、(33b)成立。由前述李亞普諾夫函數的定義可知: λmaxxT(t)Rx(t)≤V(x(t))≤λminxT(t)Rx(t) (37) (38) 即式(33c)成立,條件(22c)舒爾補化簡可得式(33d)成立,證畢。 為了驗證所建立的模糊控制器以及所設計的自觸發方案的有效性,通過數值仿真說明了該方法的可行性,單連桿剛性機器人系統驗證自觸發機制及控制器在實踐中的有效性。 數值仿真: 考慮以下具有狀態量化的T-S模糊系統: 兩條模糊規則下的系統參數矩陣如下: 不確定參數ΔAi(t)ΔBi(t)滿足(3)式定義,選取 求解把不等式(33a)~(33d),可以得到一系列可行解: K1=[-6.849 -5.856]K2=[-7.883 -5.518] 仿真結果及分析: 圖2為T-S模糊系統開環狀態軌跡圖。c1為有限時間有界的下界,c2為有限時間有界的上界,根據有限時間有界的定義,規定系統初始狀態在c1界內,在一個有限的時間區間范圍,系統的狀態軌跡始終能夠保持在預先給定的界限內。從圖2可以看出,當系統無控制輸入時,其運動軌跡超出所給的界限。圖3為T-S模糊系統閉環狀態軌跡圖。對比兩圖可知,在控制作用下,T-S模糊系統能夠達到有限時間有界,這也說明所設計的控制器的有效性。 圖2 T-S模糊系統開環狀態軌跡圖 圖3 T-S模糊系統閉環狀態軌跡圖 圖4為自觸發機制作用時所產生的觸發間隔圖。通常周期觸發方式是以一個固定時間周期進行系統觸發,這種方式就會使控制器增益按照此時間周期頻繁觸發。由圖4可知,觸發間隔均大于0,避免了芝諾行為的發生,并且可以看到t=5 s時,觸發間隔達到0.25 s并保持此值進行觸發。 圖4 自觸發時間間隔圖 一方面,由圖5得知,此時控制器增益u接近于0,此時系統達到穩定狀態,觸發時刻不變。假設以最小觸發間隔為周期觸發間隔,可以看到,在系統穩定后,觸發間隔可以達到最初的8倍左右,所設計的自觸發機制可以節約80.2%的資源。 圖5 控制器增益變化圖 另一方面,結合圖4和圖5,系統控制器增益的變化與觸發頻率呈現正相關趨勢。這也與自觸發機制自身的設計理念相吻合,模糊控制器的更新只與觸發時刻的狀態變量有關。可以看出,當系統頻繁觸發時,控制器增益數值變化率大,當控制器增益變化較小時,觸發頻率也相應減小,觸發間隔增大。通過以上分析,可以說明所設計的自觸發機制在資源利用率上更具有優勢。 實例仿真: 單連桿剛性機器人系統的動態方程如下[4]: Plant Rule 1: ifx1is about 0, then Plant Rule 2: 其中: 受控輸出方程參數選取: 不確定參數ΔAi(t)ΔBi(t)滿足(3)式定義,選取 本實驗的控制目標是在系統參數不確定并且存在外部干擾的情況下,設計一個自觸發機制及模糊控制器使得系統運動軌跡在有限時間內不會超過一定的界限,保證了系統的暫態性能。經過嚴格的數學推導,同時保證系統滿足所期待的H∞性能指標。設計該機制能夠使得系統無需依賴外部硬件設備對觸發條件進行持續監測,節約硬件資源與計算資源。 利用Matlab軟件的線性矩陣不等式工具,求解(33a)~(33d),得到如下控制器增益及自觸發參數矩陣: K1=[-0.5830 -0.5117] K2=[-0.6882 -0.3978] 將有限時間控制器增益和所提出的自觸發策略以及求解所得的自觸發參數矩陣應用到系統(8)中,來驗證所提方法的有效性。 圖6、圖7分別為參數不確定的T-S模糊系統開環、閉環狀態軌跡圖。對比兩圖可知,在所設計的自觸發機制下,施加控制作用的單連桿剛性機器人系統是滿足有限時間有界且滿足期望的性能水平。在一些活動范圍受限、執行動作精度較高的情況下,其狀態軌跡在有限時間內不超過一定的界限,這證明了該方法的可用性。而開環系統中其運動軌跡會超過所規定的界限c2。 圖6 單連桿剛性機器人系統開環狀態軌跡圖 圖7 單連桿剛性機器人系統閉環狀態軌跡圖 圖8為系統閉環狀態響應圖,圖9為觸發間隔圖。可以發現,系統在性能較差時,自觸發機制頻繁工作,觸發間隔較小。隨著系統穩定性提高,觸發間隔不斷增大,觸發次數減少。從圖5中可以看出,當時間在80 s后,觸發間隔可以達到2 s以上,使得系統觸發頻率不斷降低,假設以最初觸發間隔0.7 s為恒定采樣周期,可以得出此方法可以節省35%的資源占用,這也進一步證明了所設計的自觸發機制能夠提高資源利用率。 圖8 單連桿剛性機器人系統閉環狀態響應圖 為了減少通信資源的浪費,針對不確定性T-S模糊系統設計了一種自觸發機制。利用觸發周期不固定的特性,在能夠保障穩定性的前提下,實現控制系統的能耗優化。自觸發機制裝載在系統內部,無需額外硬件設備接收觸發信號。同時考慮外部有界干擾的存在,設計只與觸發時刻狀態有關的模糊控制器,推導了保證具有期望H∞性能水平的T-S模糊系統有限時間穩定的充分條件。通過求解一組LMI,同時獲得了有限時間H∞控制器的狀態反饋增益及自觸發參數矩陣。最后通過數值仿真及實例仿真,驗證了所建立的模糊控制器以及所設計的自觸發方案的有效性。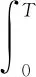

2 主要成果
2.1 自觸發機制

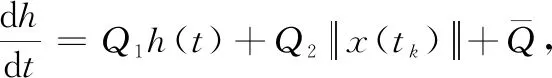
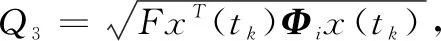
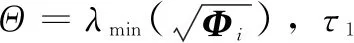
2.2 自觸發有限時間H∞性能分析
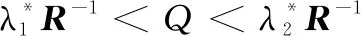



3 仿真實驗

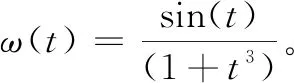



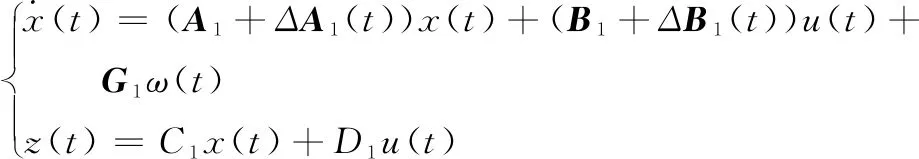
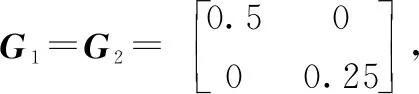
4 結束語

