基于粒子群算法的湘江船閘閘室編排算法
鄧偉 熊浩奇 余紹軍 顏淑婷
摘要:隨著水運交通的不斷發展,船閘作為重要的水利工程設施,在調節和控制船舶通行方面發揮著關鍵作用。合理且高效的船閘閘室編排對于提高船舶的通過效率具有至關重要的作用。該研究將粒子群算法引入船閘閘室編排問題中,將每個粒子視為一個可能的船閘閘室編排方案。通過不斷的迭代優化,粒子群算法能夠尋找到最優的編排方案,從而使得船舶的通過時間達到最短。文章提出的算法能夠有效地提高船舶的通過效率,優化船閘閘室的利用,具有實際應用的潛力和價值。
關鍵詞:船閘閘室編排;粒子群算法;編排問題
中圖分類號:TP311? ? ? ? 文獻標識碼:A
文章編號:1009-3044(2024)09-0012-03
開放科學(資源服務)標識碼(OSID)
1 緒論
船閘作為水運交通中的重要設施,對于船舶的順利通過和水運運輸的順暢進行起著至關重要的作用。船閘閘室編排是指根據不同船舶的尺寸、通過時間等因素,合理安排船舶在閘室中的順序和位置,旨在提高閘室利用率和船舶通過的效率[1]。然而,隨著船舶規模和運輸需求的不斷增加,傳統的船閘閘室編排方法已經難以滿足實際需求,因此需要尋求更優化的算法來解決該問題。本論文的研究目的是基于粒子群算法(PSO) 提出一種優化的湘江船閘閘室編排算法。該算法將通過數據分析和數學模型的建立,與粒子群算法相結合,以求得最優的閘室編排方案。
2 船閘閘室編排的數學模型
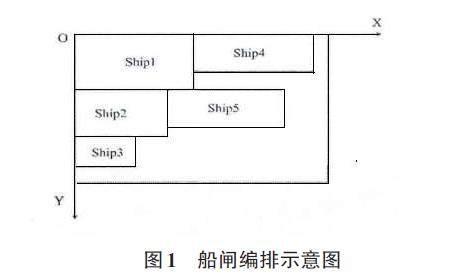
本文將船舶簡化為小矩形,因此船舶編排的過程可以簡化為小矩形填充大矩形的過程,即在編制計劃內填船(排擋),如圖1所示[2]。在計劃編制船舶時,船舶是否被選中以及選中后所處的位置都會對編排結果產生影響。
為了保證船舶先到先過原則,同時兼顧船舶優先級,通過對船舶綜合權重的計算,船舶過閘按綜合權重大小進行排序,并生成有序的船舶流。文中符號定義:i,j為船舶編號;xj為第i艘船舶以O為原點在船閘的停靠橫坐標;yi為第i艘船舶以O為原點在船閘的停靠縱坐標;ai為第i艘船舶的面積;m為己選船舶總數;n為待選船舶總數;A為船閘閘室面積;L為船閘閘室有效長度;M為船閘閘室有效寬度;leni為第i艘船的長度;widi為第i艘船的寬度[3]。
閘室編排的過程中,由于不同的船舶的進閘組合方案對于平均待閘時間影響不大,因此主要優化閘室面積利用率,閘室編排的目標是最大化閘室面積利用率,如式(1) 所示。
[maxf=i=1maiA]? ? ? ? ? (1)
選擇進入某一閘次的船舶必須滿足以下約束條件:
1) 所有選中的船舶能全部排下:
[i=1mai≤A]? ? ? ?(2)
2) 每條選中船舶的尺寸必須小于船閘的尺寸:
[0 [0 3) 所有選中的船舶放置位置不可與其他船重疊,假如船舶j是已選船舶中除i以外的任意一艘,則必須滿足: [xi+leni≤xj]或[xi≥xj+leni]或 [yi+widi≤yj]或[yi≥yj+widi]? (5) 3 船閘閘室編排的算法求解 船舶的配置方法需要考慮排隊論,假設所選船閘閘室有m個備選船舶站址,通過估算需要新增n~k(n<k) 個船舶,可得所有可能的方案有[i=nkCin]個。再進一步根據式(2) 、式(3) 、式(4) 、式(5) 的約束條件,可以篩選出一部分可行的船舶位置優化方案。對上述篩選的可行的優化方案進行計算時,只需要考慮各船舶個數在最小個數和最大個數之間這一約束條件。利用MATLAB進行編程對模型進行求解,具體求解過程如下[4]: 1) 本文將Voronoi圖進行左右分塊,進行柵格化;確定船舶坐標、船舶最大最小尺寸及船閘閘室容量以及其他相關參數;將船舶坐標、船閘閘室容量利用多維數組進行表示。 2) 將船舶坐標和船閘閘室容量等其他相關參數帶入粒子群算法,以最大化閘室面積利用率為主要優化目標,以船閘閘室容量為約束條件,搜索滿足約束條件規劃方案的最優解。 3) 得到閘室面積利用率,作為粒子群算法的適應度值,記錄個體極值和全局極值。 4) 若未達到迭代次數,則更新粒子速度與位置信息作為新的船舶編排方案,重新進行搜索。 5) 若達到迭代次數,則得到最大化閘室面積利用率的編排方案,以數據和Voronoi圖進行顯示。 利用Voronoi圖及粒子群優化算法對模型求解流程如圖2所示。 4 閘室面積利用率與待閘時間的優化 在閘室編排的過程中,閘室面積利用率與待閘時間的優化時,最大化閘室面積利用率,如式(6) 所示,平均待閘時間最短的如(7) 所示[5]。 [maxf=i=1maiA]? ? ? ?(6) [max(m/i=1mbi)]? ? ?(7) 閘室面積利用率與平均待閘時間的優化的多目標函數為: [maxλi=1maiA+(1-λ)m/(i=1mbi)]? ? (8) 其中:i為船舶編號;bi為船舶i的等待時間;[λ]為權重參數。必須滿足以下約束條件還是如式(2) ~式(5) 。 5 算法優越性驗證與結果分析 本文利用湘江船閘閘室2023年4月份的閘室使用情況,使用本文提出的粒子群算法得出結果與人工編排進行比較,如表1所示。 如表1所示,使用粒子群算法的船閘閘室容量比使用人工編排高,說明本文的算法具有很高的適應性。 在[λ]=0.5下的湘江船閘閘室利用率和等待時間情況如表2所示。 在[λ]=0.8下的湘江船閘閘室利用率和等待時間情況如表3所示。 如表2和表3所示,使用粒子群算法的船閘閘室容量比使用人工編排高而且等待時間也較人工編排短,說明本文的算法具有很高的適應性。 6 結束語 本文針對湘江船閘的閘室編排問題,提出了一種基于粒子群算法的優化方法。首先對湘江船閘的運行情況和問題進行了調研和分析,包括船舶尺寸、通過時間、閘室容量等。然后,將問題抽象成一個優化問題,并建立了適合粒子群算法優化的數學模型。接著,通過粒子群算法的初始化、迭代更新和適應度評估等步驟,尋找最優的閘室編排方案。最后,通過數值模擬和對比實驗,驗證了所提算法的有效性和性能優勢。 參考文獻: [1] 朱瑩瑩,王宇嘉.求解復雜旅行商問題的混合粒子群算法[J].輕工機械,2015,33(3):42-45,49. [2] 陽瓊芳,孫如祥. 粒子群與遺傳算法的混合算法[J]. 華僑大學學報(自然科學版),2015,36(6):645-649. [3] 李雅瓊.基于粒子群算法的遺傳算法優化研究[J].蘭州文理學院學報(自然科學版),2017,31(1):55-60. [4] 汪沖,李俊,李波,等.改進的蟻群與粒子群混合算法求解旅行商問題[J].計算機仿真,2016,33(11):274-279. [5] 李擎,張超,陳鵬,等.一種基于粒子群參數優化的改進蟻群算法[J].控制與決策,2013,28(6):873-878,883. 【通聯編輯:代影】

